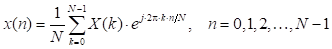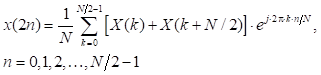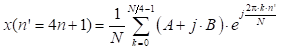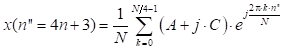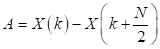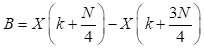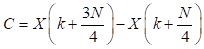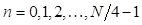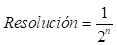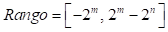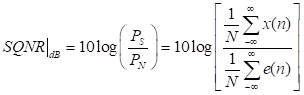Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
En la actualidad existe una gran variedad de sistemas de transmisión que hacen uso de la Multiplexación por División de Frecuencia Ortogonal (OFDM) para la transmisión de señales digitales. Sistemas ampliamente usados tales como: televisión digital terrestre ISDB-Tb, 802.16, y algunas versiones de 802.11 emplean este método que se enmarca en la aplicación de la Transformada Discreta Inversa de Fourier (IDFT), que se ejecuta en hardware gracias a la ayuda de la FFT y genera así la señal OFDM en banda base.
La FFT representa un conjunto de algoritmos que pretenden obtener la Transformada discreta de Fourier (DFT) a través de un menor número de operaciones, lo cual implica una menor cantidad de recursos y bajos tiempos de cálculo en las implementaciones en hardware. Para tales efectos, la mayoría de los algoritmos FFT descompone de forma recursiva la DFT de tamaño N, en varias DFT de menor longitud n. La manera en que se lleva a cabo dicha descomposición da lugar a la aparición de dos tipos básicos de algoritmos: diezmado en tiempo (DIT) 1 y diezmado en frecuencia (DIF) 1.
La descomposición a la que se hace referencia en el párrafo anterior es posible aplicar siempre y cuando N sea factorizable. Así por ejemplo, si N es una potencia de dos o cuatro, se pueden tener los algoritmos radix-2 2 o radix-43, respectivamente. Con base en ellos, Pierre Duhamel desarrolló el algoritmo Split-radix asimétrico 4 y una variante de éste, conocido como Split-radix simétrico 5.
Respecto al algoritmo Split-radix asimétrico, Erkan İnceöz lo implementa en una FPGA, mediante una arquitectura en paralelo con alta velocidad de cómputo para una FFT de longitud variable que llegó hasta los 1024 puntos 6.
En 7 se realiza una implementación del Split-radix asimétrico mediante la utilización de aritmética distribuida para mejorar los multiplicadores de las dos arquitecturas pipelined (en paralelo) que proponen en su trabajo de investigación y aumentar así la velocidad de cómputo. Presentan resultados únicamente para N= 32 puntos.
Por otra parte, Zhuo Qian 8, implementa una arquitectura en paralelo del Split-radix asimétrico enfocándose en la reducción del consumo de potencia, pero a costo de usar más recursos del hardware. Los resultados de la potencia consumida y los recursos ocupados los compara con trabajos previos para una transformada de 1024.
En 9, se desarrolla una arquitectura en paralelo del algoritmo Split-radix asimétrico, la cual permite calcular como máximo una transformada de 256 puntos, pero a gran velocidad y con un reducido consumo de potencia.
En este artículo se propone el desarrollo en VHDL (VHSIC Hardware Description Language) y la evaluación en hardware de una arquitectura que realice el cómputo de la IFFT con los algoritmos Split-radix simétrico y asimétrico para el estándar de televisión ISDB-Tb, con la finalidad de establecer su desempeño frente a los usados por el core de Xilinx: radix-2 lite, radix-2, radix-4 y pipelined.
El presente artículo está organizado de la siguiente manera: en la Sección II se presentan los fundamentos básicos de la IFFT, y se describen los algoritmos Split-radix asimétrico y simétrico. En la Sección III se describe el procedimiento de desarrollo de los algoritmos en VHDL, mientras que en la Sección IV se trata acerca del proceso de generación de las señales de prueba, y finalmente en la Sección V se evalúan los Split-radix para posteriormente generar las conclusiones del artículo en la Sección VI.
Transformada Discreta de Fourier
Para iniciar con el análisis de los algoritmos Split-radix, es necesario plantear primeramente la expresión matemática que define la IDFT como se muestra en (1):
donde x(n) es la secuencia de N muestras de la señal en el dominio del tiempo discreto n, y X(k) representa la secuencia de N muestras en el dominio de la frecuencia discreta k.
Para calcular la IDFT de una secuencia de N valores complejos, se necesitarán N 2 multiplicaciones complejas y N(N-1) sumas complejas. Si N es un valor grande, se tendría que ejecutar un número muy elevado de operaciones. Para reducir este consumo de recursos se han propuesto varios algoritmos, uno de ellos es el algoritmo Split-radix en sus dos versiones asimétrico y simétrico, los cuales se describen a continuación.
Algoritmo Split-Radix Asimétrico
El algoritmo Split-radix resulta de la combinación del radix-2 y el radix-4. El cálculo de las muestras pares con la IDFT se realiza a partir de la siguiente expresión:
La ecuación (2) se obtiene al dividir el sumatorio de (1) en dos partes (radix-2) y al considerar la periodicidad de la expresión exponencial que se denomina factor de giro. En cuanto a las muestras impares, se dividen en 2 grupos: (4n + 1), (4n + 3) y se determinan con las expresiones (3) y (4), respectivamente. Estas expresiones se determinan al emplear el algoritmo radix-4, se componen de una parte real y una imaginaria. Al considerar la periodicidad de la expresión exponencial en los valores j0, jπ/2, jπ y j3π/2, queda de la siguiente manera:
Las expresiones (2), (3) y (4) constituyen IDFTs en las cuales se puede aplicar una división recursiva para obtener IDFTs de menor orden. En el algoritmo Split-radix, el número de etapas recursivas se obtiene considerando la relación log 2 N. Como se trata de un diezmado en tiempo, al final la secuencia de salida x(n) quedará en un orden inverso de bit, por lo cual se requerirá de un proceso adicional para lograr el orden adecuado.
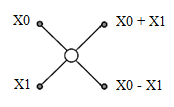
En el trabajo de Duhamel y Hollman 5, se presenta tanto el diagrama del algoritmo Split-radix asimétrico, para una IDFT de 32 puntos, así como, la estructura de cálculo básica de este algoritmo, llamada mariposa Split-radix asimétrica como se observa en la Fig. 1.
Para llevar a cabo el cálculo de los puntos de la transformada, el algoritmo Split-radix realiza una segmentación de los mismos para realizar las operaciones de mariposa en diferentes bloques. Así por ejemplo, en la etapa 0, del trabajo de Duhamel y Hollman, se tiene un solo bloque conformado por 16 mariposas.
Una particularidad que tiene este algoritmo, es que dentro de cada una de sus etapas, las mariposas no siguen un patrón determinado, es decir, no están separadas entre sí por una misma cantidad de puntos. Por ejemplo, en la etapa 4, descrita en el trabajo de Duhamel y Hollman, el primer bloque de mariposas está separado del segundo grupo por cuatro puntos; se esperaría que entre el segundo y tercero hubiese la misma cantidad de puntos y así sucesivamente hasta llegar al último grupo de la etapa en cuestión, pero esto no ocurre, la ubicación de los bloques no sigue un patrón definido y es por ello que a este algoritmo, con grupos de mariposas en forma de “L”, se lo conoce también como Split-radix asimétrico.
Algoritmo Split-radix simétrico
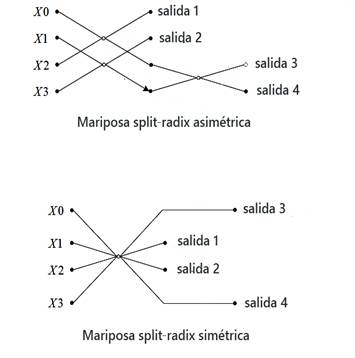
La disposición de los bloques de mariposas en el Split-radix asimétrico dificulta su implementación, no obstante, se puede incrementar la regularidad del algoritmo al permutar las salidas de la mariposa correspondiente al Split-radix asimétrico 4 para dar lugar a la mariposa simétrica, con la que se obtiene el diagrama del Split-radix simétrico descrito en 5.
En la Fig.2 se puede observar lo expuesto en el párrafo anterior, se puede apreciar como las salidas de ambas mariposas son las mismas, solo que el orden ha cambiado.
Al aplicar este cambio de mariposas, se puede observar que la estructura del algoritmo ha cambiado y se ha producido un incremento en la regularidad del mismo, al mantener el número de productos y sumas complejas requeridas para el cálculo de la transformada. La regularidad se basa en que los bloques de cada etapa están separados por una misma cantidad de puntos, lo que permite hacer más fácil su implementación en hardware.
Desarrollo de los Algoritmos Split-Radix en VHDL
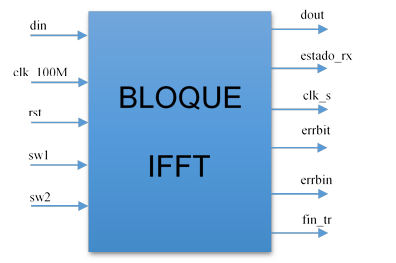
Para el desarrollo de los algoritmos Split-radix en VHDL se ha nombrado a la entidad que corresponde a la IFFT, como “bloque IFFT”, la misma cuenta con los puertos de entrada y salida que siguen la asignación presentada en la Fig. 3.
La descripción de cada uno de los puertos mostrados en la figura anterior, se expone en la Tabla 1 11.
Tabla 1: Descripción de los Puertos de la Entidad Transformada 11.
| Puerto | Descripción |
| Din | Flujo de bits de datos, que ingresan de forma serial, provenientes de MATLAB. |
| clk_100M | Utilizado para la entrada del reloj del sistema de 100 MHz de frecuencia. |
| Rst | Se emplea para reiniciar el bloque IFFT con sus valores originales. Se activa con 1L. |
| sw1 y sw2 | Se usan para la selección del modo de transmisión bajo el cual operará el bloque IFFT. |
| Dout | Usado para enviar de forma serial los bits de los datos obtenidos luego de efectuar la IFFT. |
| estado_rx | Si su valor es de 1L, indica que no se están recibiendo datos por el puerto din. |
| clk_s | Salida del reloj de 9600 Hz para la comunicación serial. |
| Errbit | Toma el valor de 1L cuando se han recibido bits errados. |
| Errbin | Se pone a 1L cuando se ha recibido una cantidad de símbolos complejos que no corresponden al modo de transmisión seleccionado. |
| fin_tr | Toma el valor de 1L en el momento en que concluye el cálculo de la IFFT. |
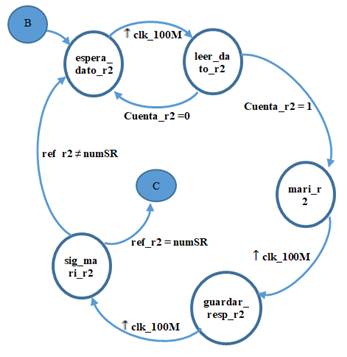
La mayoría de los procesos para ejecutar la transformada se encuentran controlados por máquinas de estados finitos (FSM) 10, que permiten la implementación de circuitos secuenciales. En la Fig. 4, como referencia, se presenta una de las máquinas de estados para el cálculo de la transformada.
Los conectores B y C representan estados de otras FSM implementadas para el cálculo de la transformada. Clk_100M es la señal de reloj de 100 MHz de la FPGA, numSR es una variable donde se almacena el número de mariposas de la última etapa; Cuenta_r2 es una variable acumulativa donde se guarda el número de datos que ingresan a la mariposa; finalmente ref_r2 es otra variable acumulativa donde se tiene el número de mariposas que se van calculando a lo largo de cada etapa.
Las acciones que se llevan a cabo en cada uno de los estados se describen a continuación:
Espera_dato_r2: Estado de espera de un ciclo de reloj hasta tener un dato válido en el puerto de la RAM Bins_resp, que contiene la parte real e imaginaria de los símbolos complejos que ingresan a la transformada.
Leer_dato_r2: En dos ciclos de reloj se leen los 2 datos de Bins_resp, que corresponden a las dos entradas para una mariposa radix-2 de la última etapa del algoritmo Split-radix asimétrico.
Mari_r2: Se efectúan las operaciones que comprenden una mariposa radix-2, al tiempo que se guarda en Bins_resp, la primera salida de dicha mariposa.
Guardar_resp_r2: Se almacena en Bins_resp la segunda salida de la mariposa.
Sig_mari_r2: Se chequea si aún faltan por calcularse mariposas radix_2. De ser así, se ubica a la siguiente mariposa, con ayuda de las señales pilotos.
De la figura anterior, es importante señalar que para pasar de un estado a otro, hay casos en los que no se requiere que se cumpla alguna condición, simplemente, se da una transición positiva del reloj de Clk_100M y se produce el cambio de estado. Esto es así porque se requiere de un retardo de un ciclo de reloj para leer y guardar datos en las memorias RAM.
En 11 se presenta una descripción más detallada de todo el proceso de implementación de los algoritmos Split-radix en VHDL.
Evaluación de los Algoritmos Split-Radix
Equipamiento utilizado
Para la implementación y pruebas de los algoritmos IFFT se emplearon los elementos que se muestran en la Fig. 5 y que se enumeran a continuación: Computadora con MATLAB R2013b (donde se genera el símbolo OFDM), tarjeta FPGA Virtex-5 XUPV5-LX110T (donde se encuentra la arquitectura que calcula la IFFT), fuente de alimentación de 6 Amperios, tarjeta flash de 1GB, cable XUP JTAG - USB, cable USB - serial RS-232 (terminal macho) y cable RS-232 con terminales hembra.
El montaje expuesto en la figura anterior tiene como objetivo principal la comparación entre los algoritmos Split-radix y los del core FFT de Xilinx, medir la cantidad de recursos que ocupa cada uno, su nivel de SQNR y tiempos de ejecución para cada modo de transmisión del sistema ISDB-Tb.
La metodología que se sigue para la evaluación de los algoritmos es la siguiente:
Se inicia generando un símbolo OFDM de prueba en una PC mediante MATLAB para cada modo de transmisión.
El símbolo se envía de forma serial a la tarjeta FPGA, en la que se ejecuta cada uno de los algoritmos de la IFFT (los Split-radix y los del core de Xilinx)
El resultado del cálculo efectuado en la FPGA se envía de vuelta al computador para calcular el nivel de SQNR usando como referencia la IFFT obtenida a través de MATLAB.
A continuación, se explicará a detalle cómo se genera el símbolo OFDM, cuales son los modos de transmisión y la forma de obtener el SQNR.
Modos de transmisión y generación del símbolo OFDM de prueba
Para probar el funcionamiento de los algoritmos, en un computador con el software MATLAB se generó un símbolo OFDM de prueba para cada uno de los tres modos de transmisión del estándar ISDBT-b. Los modos de transmisión de dicho estándar se caracterizan por establecer 1405 subportadoras en el modo 1, 2809 subportadoras en el modo 2 y 5617 subpotadoras en el modo 3. El símbolo generado se envía por medio del puerto serial hacia la FPGA para el cálculo de la IFFT. Pero para efectuar dicho cálculo, en cada modo se agregan ceros hasta obtener potencias de dos, quedando un total de 2048 (211) subportadoras en el modo 1, 4096 (212) subportadoras en el modo 2 y 8192 (213) subportadoras en el modo 3.
El símbolo OFDM generado puede ser mapeado mediante QPSK, 16-QAM o 64-QAM. Los símbolos complejos que resultan del mapeo se transforman de formato decimal a binario, para lo cual se utiliza una representación en punto fijo 12.
La representación en punto fijo equivale a un proceso de cuantización, pues se toma un número y se hace corresponder el mismo con el valor más próximo de entre un conjunto de valores preestablecidos (valores de cuantización), los cuales son completamente dependientes del número m de bits de la parte entera y n de bits de la parte fraccionaria, por medio de los que se obtienen las expresiones (9) y (10) para calcular el rango y la resolución de la cuantización.
La resolución es la distancia más pequeña existente entre dos valores de cuantización consecutivos; es decir, es el tamaño de paso del cuantizador y se obtiene mediante la siguiente expresión:
El rango corresponde al conjunto de todos los números posibles que se pueden representar con una determinada cantidad de bits; los límites inferior y superior del rango, están dados por:
Con base en lo anterior, se decidió representar los símbolos complejos (obtenidos después del mapeo) con un total de 16 bits para la parte real y 16 bits para la parte imaginaria. La asignación de bit para dichos símbolos se lleva a cabo de la siguiente manera: 1 bit para el signo, 1 bit para la parte entera y 14 bits para la fracción. Una vez que los valores complejos que conforman el símbolo OFDM son representados en punto fijo, se envían de forma serial hacia Matlab®.
Almacenamiento de los datos en la FPGA
Para el almacenamiento de los datos recibidos desde MATLAB en la FPGA, y para guardar los resultados obtenidos después de la aplicación de los algoritmos IFFT, se utiliza una memoria RAM de 8192 posiciones (cada una de 32 bits). El procedimiento antes mencionado implica que cada vez que llega un nuevo dato, el mismo se direcciona a la RAM y se almacena en una de las localidades al concatenar la parte real e imaginaria.
Los factores de giro para cada modo de transmisión, que corresponden a los términos exponenciales de las expresiones (2), (3) y (4) de los algoritmos Split-radix, se generaron en Matlab y se almacenaron en la memoria ROM de la FPGA. Cada localidad de la ROM cuenta con 32 bits, donde los 16 más significativos corresponden a la parte real del factor de giro y los 16 menos significativos a la parte imaginaria. Cada factor, al igual que los valores complejos del símbolo OFDM, está expresado en formato de punto fijo con signo de 16 bits (1 para la parte entera y 14 para la fraccionaria). En el caso de las arquitecturas del bloque de Xilinx, no es necesaria la ROM de los factores de giro, pues dicho bloque ya cuenta con una memoria que cumple con esa función.
Relación señal a ruido de cuantización
Un aspecto fundamental a tener en cuenta para la evaluación de los algoritmos es el error de cuantización, que constituye el ruido generado al asignar los valores de equivalencia en cada rango a lo largo de todo el proceso de cuantización. Para medir dicho error, se usa la SQNR (Relación Señal a Ruido de Cuantización) sobre los N valores de una secuencia x(n) cuantizada. La SQNR se calcula mediante la ecuación que se presenta a continuación:
(11)
donde PS es la potencia de la señal cuantizada, PN es la potencia del ruido generado por efecto de la cuantización,
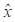(n) es la señal antes de la cuantización, x(n) es la señal después de la cuantización y e(n) es el error de cuantización, que se obtiene de la diferencia entre
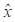(n) y x(n).
Entonces, en el caso de los algoritmos, x(n) es la IFFT obtenida en la FPGA, mientras que
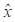(n) es el resultado que arroja Matlab®.
Resultados de la Evaluación de los Algoritmos
A continuación, se presentan los resultados de las pruebas ejecutadas a los algoritmos IFFT que fueron implementados en la tarjeta FPGA Virtex-5. Para evaluar los resultados del cálculo de la IFFT obtenidos con los algoritmos, se implementaron seis proyectos en total, dos correspondientes a los algoritmos Split-radix simétrico y asimétrico; y, cuatro proyectos para las arquitecturas del bloque FFT disponibles en las herramientas de Xilinx: Radix-4 Burst I/O, Radix-2 Burst I/O, Radix-2 Lite Burst I/O y Pipelined streaming I/O.
En la Tabla 2 se presenta el resumen de los recursos utilizados de la tarjeta FPGA por cada uno de los algoritmos.
Tabla 2: Porcentaje de Recursos Utilizados por los Algoritmos de la IFFT
| Tipo de recurso | Split-radix asimétrico | Split-radix simétrico | Radix-2 lite | Radix-2 | Radix-4 | Pipelined |
| Slices | 5% | 7% | 3% | 3% | 6% | 17% |
| Flip flops | 1% | 1% | 2% | 2% | 4% | 11% |
| LUTs | 3% | 5% | 2% | 2% | 3% | 9% |
| bloques RAM | 7% | 12% | 11% | 11% | 12% | 17% |
| DSP48E | 15% | 15% | 3% | 4% | 14% | 28% |
Al comparar los algoritmos Split-radix se observa que su versión simétrica es la que más recursos consume, tal y como se esperaba, ya que ésta necesita de una lógica adicional para colocar el resultado en orden natural. En cambio, al comparar todos los algoritmos, el radix-2 lite es el que menos recursos necesita, mientras que el pipelined constituye el algoritmo que mayor cantidad de recursos requiere. Se observa que los algoritmos Split-radix con respecto a utilización de recursos se ubican entre los algoritmos radix-4 y el pipelined.
En las Tabla 3, Tabla 4 y Tabla 5 se presentan los valores de SQNR obtenidos del cálculo de la IFFT con los algoritmos para las modulaciones QPSK, 16-QAM y 64-QAM respectivamente. Dichos valores constituyen el promedio obtenido de diez pruebas realizadas, debido a que los datos generados en Matlab para la formación del símbolo OFDM son aleatorios.
De los resultados se aprecia que los algoritmos Split-radix son los que más alto SQNR presentan, además se observa que a medida que aumenta el modo de transmisión o la longitud de la secuencia de entrada al bloque IFFT, disminuye el SQNR aproximadamente en 4 dB.
Como parte de la evaluación planteada en este trabajo, en la Tabla VI se presentan los tiempos de procesamiento requeridos para la ejecución de los algoritmos de la IFFT en los tres modos de transmisión. De los valores obtenidos se puede mencionar que el algoritmo que se ejecuta más rápido es el Pipelined, mientras que los algoritmos que requieren mayor tiempo de procesamiento son: Split-radix asimétrico y simétrico. Esto se debe a 3 factores cruciales: primero, que en estos algoritmos el cálculo se realiza de forma secuencial, segundo, que en la programación se cuenta con el cálculo de una mariposa Split-radix, y tercero, que los datos de entrada así como los que se generan al término de cada etapa se guardan en una misma memoria, por lo que para leer las cuatro entradas de la mariposa o almacenar sus salidas, se necesitan de cuatro ciclos de reloj.
Tabla 3: Valores de SQNR en dB del Cálculo de la IFFT con los Algoritmos para QPSK
| Arquitectura | Modo 1 | Modo 2 | Modo 3 |
| Split-radix asimétrico | 52.29 | 48.62 | 45.51 |
| Split-radix simétrico | 52.19 | 48.67 | 45.63 |
| Radix-2 lite | 44.49 | 40.5 | 38.4 |
| Radix-2 | 44.51 | 44.47 | 38.49 |
| Radix-4 | 42.57 | 43.56 | 35.48 |
| Pipelined | 47.39 | 44.44 | 41.3 |
Tabla 4: Valores de SQNR en dB del Cálculo de la IFFT con los Algoritmos para 16-QAM
| Arquitectura | Modo 1 | Modo 2 | Modo 3 |
| Split-radix asimétrico | 54.34 | 51.52 | 48.55 |
| Split-radix simétrico | 54.38 | 51.22 | 48.47 |
| Radix-2 lite | 47.45 | 43.69 | 40.63 |
| Radix-2 | 47.5 | 43.47 | 40.48 |
| Radix-4 | 44.44 | 45.46 | 37.47 |
| Pipelined | 49.53 | 47.43 | 43.53 |
Tabla 5: Valores de SQNR en dB del Cálculo de la IFFT con los Algoritmos para 64-QAM
| Arquitectura | Modo 1 | Modo 2 | Modo 3 |
| Split-radix asimétrico | 54.34 | 51.52 | 48.55 |
| Split-radix simétrico | 54.38 | 51.22 | 48.47 |
| Radix-2 lite | 47.45 | 43.69 | 40.63 |
| Radix-2 | 47.5 | 43.47 | 40.48 |
| Radix-4 | 44.44 | 45.46 | 37.47 |
| Pipelined | 49.53 | 47.43 | 43.53 |
Tabla 6: Tiempo de Procesamiento en Microsegundos Requerido para la Ejecución de los Algoritmos de la IFFT
| Arquitectura | Modo 1 | Modo 2 | Modo 3 |
| Split-radix asimétrico | 490.85 | 855.96 | 1848.25 |
| Split-radix simétrico | 527.19 | 1142.6 | 2462.4 |
| Radix-2 lite | 267.71 | 575.03 | 1230.51 |
| Radix-2 | 155.42 | 329.66 | 698.46 |
| Radix-4 | 72.9 | 144.58 | 308.61 |
| Pipelined | 62.79 | 124.39 | 247.27 |
Finalmente, en la Tabla 7 se presenta una comparación entre los algoritmos Split-radix del presente trabajo con el propuesto en la referencia 6, al tomar en cuenta el número de ciclos de reloj que le toma a cada uno efectuar el cálculo de la IFFT. Se observa que a los algoritmos Split-radix les toma más ciclos de reloj efectuar la transformada, ya que se utilizó una arquitectura secuencial con la finalidad de utilizar la menor cantidad de recursos de la tarjeta empleada, a diferencia en 6 se implementó una arquitectura en paralelo lográndose una ejecución más rápida.
En la tabla 7 no se establece una comparación con 7, 8 y 9, ya que en esos trabajos no se realizaron implementaciones iguales o superiores a 1024 puntos.
Tabla 7: Ciclos de Reloj Requeridos para la Obtención de la IFFT
| Arquitectura | N=1024 | N= 2048 | N=4096 | N=8192 |
| Split-radix asimétrico | 17250 | 49085 | 85596 | 184825 |
| Split-radix simétrico | 24500 | 52719 | 114260 | 246240 |
| Split-radix asimétrico (6) | 13551 | N/A | N/A | N/A |
Conclusiones
De las pruebas realizadas se puede concluir que con la programación propuesta en este proyecto, los algoritmos Split-radix, utilizan una cantidad media de recursos de la tarjeta FPGA en comparación a otros algoritmos existentes para el cálculo de la IFFT de un símbolo OFDM del estándar ISDBT-b. Comparada con 6, nuestra implementación requiere más ciclos de reloj, ya que la arquitectura propuesta en el presente trabajo no es en paralelo sino secuencial para tratar de optimizar los recursos utilizados. Además, se observa que, a diferencia de los trabajos mencionados en la bibliografía, en nuestro proyecto se implementa tanto el Split-radix simétrico como el asímétrico, permitiendo el cálculo de transformadas superiores a 1024 puntos (2048, 4096 y 8192) y se incluye un parámetro de análisis comparativo adicional como es el nivel de ruido SQNR generado por la representación en punto fijo de los datos. Además del análisis se obtuvo que el algoritmo que ocupa la menor cantidad de recursos de la tarjeta FPGA es el radix-2 lite. Se puede decir también que del análisis comparativo se observó que los algoritmos Split-radix permiten alcanzar un valor de SQNR más alto que el obtenido para los demás algoritmos, lo que implica que el error en el cálculo de la IFFT es menor en comparación a los otros algoritmos probados. Además, se tiene que al aumentar el modo de transmisión, en todos los algoritmos disminuye la precisión del cálculo de la IFFT, reflejándose en una disminución del SQNR en aproximadamente 4dB. Esto se debe a que el número de etapas requeridas para el cálculo se incrementa, y por ende el número de operaciones, con lo cual el error aumenta, disminuyendo el nivel de SQNR. Finalmente, del análisis realizado se obtiene que el algoritmo que ejecuta el cálculo más rápido es el Pipelined, mientras que los algoritmos que requieren más tiempo de procesamiento son los Split-radix.
