Introducción

El desarrollo de técnicas para el diseño de sistemas de control multivariable es de práctica común para sistemas complejos. Un método particular de diseño, es aquel que implica el uso de realimentación para conseguir estabilidad de sistemas de control de lazo cerrado (^{Ogata, 2008}). Con este método es a menudo de interés conocer si es posible o no lograr que las entradas controlen a las salidas independientemente, esto es, que una sola entrada influya en una sola salida (i.e., el tener un sistema desacoplado). Ya conseguido el desacoplamiento de un sistema multivariable MIMO (Multiple Input - Multiple Output), puede ser analizado mediante las técnicas clásicas para sistemas SISO (Single Input - Single Output) (^{Granizo, 1988}).

La problemática de desacoplar un sistema MIMO mediante el proceso analítico algebraico (^{Granizo, 1988}), es muy complicado y al mismo tiempo se alarga, a la vez que se aumente el número de entradas que es igual al número de salidas, y más por supuesto, si se aumenta también el orden del sistema (^{Montgomerie & Nicholson, 2015}).

Una de las formas para determinar el "desacoplamiento" de un sistema multivariable, es la técnica matriz función de transferencia mediante el análisis algebraico (^{Chen, 1970}), que para sistemas de dos entradas y dos salidas, son aplicaciones de fácil resolución; sin embargo, para sistemas de mayor número de entradas y salidas se recomienda el empleo de algoritmos computacionales, debido a que los elementos de las matrices son fracciones de polinomios, y por consiguiente, las operaciones matriciales normalmente son aplicadas a elementos numéricos (^{Frank, 1992}). Este trabajo desarrolla e implementa un programa computacional en lenguaje Pascal que determina un compensador de lazo cerrado que permite que el sistema acoplado multivariable pueda convertirse en un sistema desacoplado.

Con lo indicado anteriormente, un sistema multivariable de orden n, con m entradas y m salidas, en el que se asume m ≤ n, se define la matriz cuadrada función de transferencia G (s), que relaciona el vector de entrada m dimensional u (s) y el vector de salida m dimensional y (s), de la siguiente forma:

donde para que el sistema multivariable sea desacoplado, la matriz función de transferencia G (s) debe ser diagonal y no singular (^{Montgomerie and Nicholson, 2015}).

Del estudio del estado del arte en esta temática, no se ha encontrado algoritmos computacionales implementados en lenguajes de computación de alto nivel, que solucionen el desacoplamiento de sistemas multivariables.

El artículo tiene la siguiente estructura: en la sección II se trata brevemente la técnica de desacoplamiento mediante función de transferencia. En la sección III se expone la propuesta del algoritmo computacional de desacoplamiento de sistemas lineales invariantes en el tiempo (Linear Time-Invariant, LTI). En la sección IV se muestran los resultados que se obtienen al aplicar la propuesta del algoritmo computacional a sistemas MIMO. Finalmente, en la sección V se resumen las principales conclusiones de trabajo de investigación

Desacoplamiento de Sistemas Mimo por Matriz Función de Transferencia

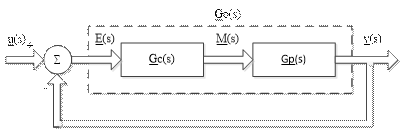
El desacoplamiento de sistemas MIMO por este método, consiste en obtener una matriz compensadora Gc (s) de dimensión (n x n) serie a la función de transferencia de paso directo Gp (s), tal que la matriz del sistema de lazo cerrado sea diagonal (^{Montgomerie and Nicholson, 2015}), como se puede observar en la Fig 1.

Fig 1 Sistema multivariable de orden n con realimentación unitaria y compensador serie. 

Donde u (s) es el vector de entrada n dimensional, y (s) es el vector de salida n dimensional, E (s) es el error entre el vector de entrada y el vector de salida, de orden n , M (s), es la nueva entrada de la planta Gp (s), Go (s) es la matriz función de transferencia de paso directo cuando se añade un compensador y Gp (s) es la matriz función de transferencia de paso directo de dimensión ( n x n ) de una planta.

El proceso para obtener el compensador Gc (s) se muestra a continuación, se debe tener en cuenta que cada elemento de la matriz Gp (s) es un polinomio en el dominio de s y que I es la matriz identidad (^{Montgomerie and Nicholson, 2015}):

La matriz diagonal G _d (s) es conocida por imposición de diseño en el desacoplamiento de sistemas MIMO mediante función de transferencia, es decir, cada término de la diagonal de G _d (s) corresponde con las especificaciones de diseño para que el sistema cumpla con las características, tales como: estabilidad relativa, velocidad de respuesta, entre otras.

Propuesta del Algoritmo Computacional de Desacoplamiento

La propuesta del algoritmo computacional para el desacoplamiento de sistemas MIMO mediante función de transferencia, se resume en los siguientes aspectos: algoritmo computacional principal, diagrama de flujo resumido del algoritmo principal y las subrutinas utilizadas. En los siguientes literales se describe cada aspecto:

El algoritmo computacional principal

El algoritmo computacional principal propuesto para el desacoplamiento de sistemas MIMO mediante función de transferencia, se muestra a continuación:

Entrada del orden de la matriz Gp (s), que corresponde al número de entradas o salidas del sistema, que se define con ENT#091;nENT#093;.

Entrada del mayor grado de los elementos de la planta Gp (s), luego de determinar el mínimo común múltiplo de sus denominadores, que se define con ENT#091;mENT#093;.

Entrada del mayor grado del mínimo común múltiplo de los denominadores de Gp (s), que es el orden del sistema, y se define con ENT#091;tENT#093;.

Entrada del mayor grado entre los numeradores y denominadores de los términos de la matriz diagonal Gd (s), que se define con ENT#091;m1ENT#093;.

Entrada de la matriz GpL (s), de dimensión ( n x n x m ) que es la matriz Gp (s) sin el mínimo común múltiplo de sus denominadores. m son planos que corresponden al grado de los polinomios de la matriz GpL (s) en s .

Entrada del mínimo común denominador, δ (s), de orden t .

Entrada de la matriz diagonal G _d (s), que tiene dimensión ( n x n x m1 ). m1 es similar a m .

Determinar la matriz Go (s), mediante:

donde:

Numerador _i de Go (s) = n _ii (s) ,i = 1, 2,...,n

Denominador _i de Go (s) = d _ii (s) - n _ii (s) ,i = 1, 2,...,n

Determinar la matriz GpL^-1 (s), mediante la subrutina: MatrizInversaPolinomial .

Determinar la matriz Gc (s), mediante el siguiente proceso:

10.1) Calcular:

nu _j (s) = δ(s) n _jj (s) , j = 1, 2, ... , n

10.2) Calcular denominador de Gc (s),

den _j (s) = dpl(s) ENT#091;d _jj (s) - n _jj (s)ENT#093; , j = 1, 2, ... ,n.

Siendo: i = Fila de matriz.

j = Columna de matriz.

Donde dpl(s), es mínimo común denominador de la matriz GpL^-1(s)

10.3) Calcular numerador de Gc (s),

num _ij (s) = nu _j (s) gl _ij (s) , i = 1, 2, ... , n

, j = 1, 2, ... , n

Donde gl _ij (s), son los elementos de la matriz GpL^-1 (s), sin la relación: δ(s) / dpl(s)

Obtener los compensadores PID,

P _k = num _ij (s) / den _j (s) , i = 1, 2, ... , n

, j = 1, 2, ... , n

, k = -1, 0, 1, 2.

Gc _ijk = P _k , i = 1, 2, ... , n

, j = 1, 2, ... , n

, k = -1, 0, 1, 2.

Imprimir el compensador serie Gc (s).

Fin.

Diagrama de flujo resumido del algoritmo principal

El diagrama de flujo resumido del algoritmo principal de la técnica desacoplamiento matriz función de transferencia, se muestra en la Fig 2.

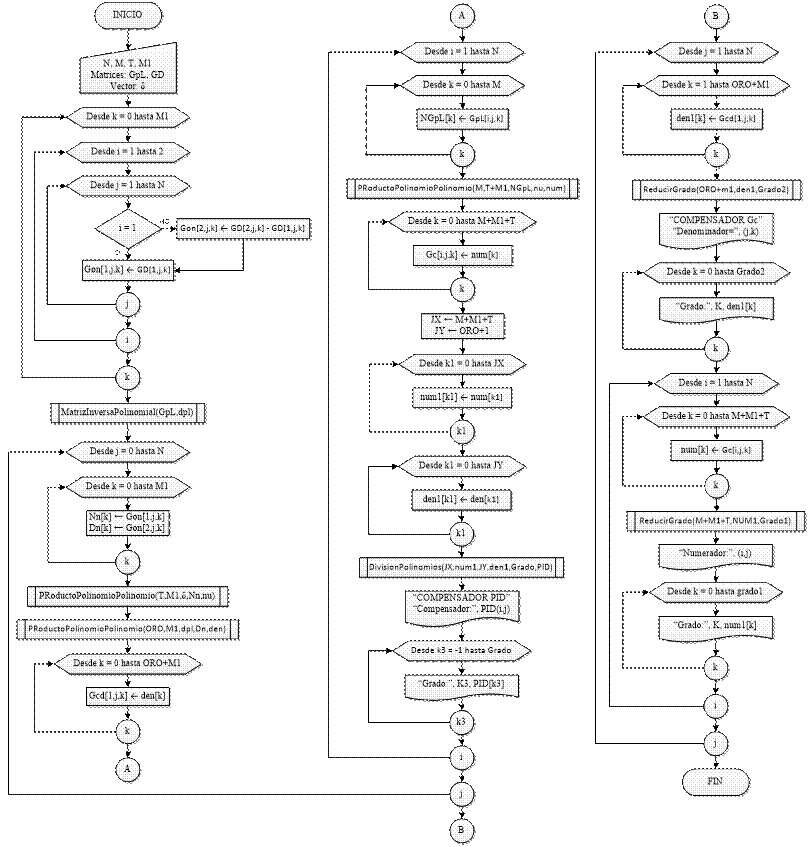
Fig 2 Diagrama de flujo resumido del algoritmo principal de la técnica desacoplamiento matriz función de transferencia. 

Las subrutinas utilizadas

Las subrutinas utilizadas en este método de desacoplamiento de sistemas MIMO, se describen a continuación:

Resultados Al Aplicar El Algoritmo Computacional

El programa computacional propuesto es muy amigable y de fácil uso, porque está implementado en lenguaje Pascal en modo consola, con la ventaja que puede ser implementado en cualquier Sistema Operativo de Windows. El limitante de este programa consiste en que no se puede utilizar en el caso de matrices no invertibles de la planta.

La matriz polinomial de la planta Gp (s) debe estar expresada de la siguiente forma:

donde GpL es la matriz polinomial en el dominio de s del numerador de la planta Gp (s) y DELTA es el polinomio mínimo común múltiplo de los denominadores de los elementos de la planta Gp (s).

Para introducir los datos de la matriz GpL, debe tenerse en cuenta que esta matriz tiene tres dimensiones, donde la tercera dimensión representa las matrices o planos que corresponden al grado creciente de los polinomios en el dominio de s .

Se recomienda que los valores de las entradas de datos: grado de la matriz Gp (N), mayor grado de los elementos de la matriz Gp una vez encontrado el mínimo común múltiplo de los deno minadores (M), y mayor grado de los numeradores y denominadores de los elementos de la matriz diagonal G _d (M1); no sobrepasen del valor de 10, debido a que el ingreso de la información es demasiado extenso y los resultados no se presentan de forma clara.

A continuación se presenta un ejemplo de aplicación que tiene el fin de comprobar que el algoritmo computacional cumple con el método matemático. Cabe destacar que el algoritmo computacional puede resolver ejercicios de grado mayor a dos, porque el programa computacional pue de aplicarse, no sólo a sistemas simples, sino también a sistemas complejos; cuyo desarrollo algebraico se tornaría largo y difícil, o inclusive impracticable.

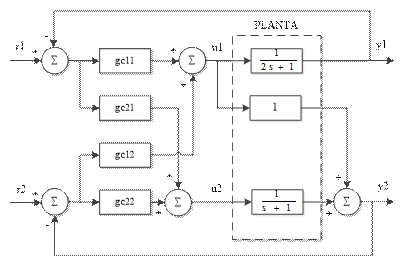
Sea el sistema MIMO de la Fig. 3, que está conformado por un sistema de dos entradas y dos salidas, con una matriz compensadora serie cuyos elementos son: gc₁₁, gc₂₁, gc₁₂ y gc₂₂.

Se determina la matriz del compensador serie Gc (s) del sistema de la Figura 3, tal que la matriz de la función de transferencia de lazo cerrado G _d (s), debe ser diagonal por diseño para que el sistema sea desacoplado, es decir, el sistema tenga cada salida dependiente únicamente de una entrada:

Fig 3 Sistema de dos entradas y dos salidas, con compensador serie. 

Por lo que al aplicar el método matemático descrito en (^{Montgomerie and Nicholson, 2015}), se obtiene la matriz del compensador serie Gc (s) añadido a la planta Gp (s):

Los elementos de la matriz (6) del compensador serie Gc(s) corresponden a los compensadores indicados en la Figura 3, los cuales tienen las estrategias de control proporcional, integral y derivativo (PID): gc ₁₁ (s)=2 + s ^-1 y gc ₂₂ (s)=0.2 + 0.2s ^-1 es control proporcional e integral; gc ₂₁ (s) = -2s - 3 - s ^-1 es control proporcional, integral y derivativo; y gc ₁₂ (s) = 0 indica no hay compensador.

En el análisis realizado no se consideran perturbaciones externas, y además se producen cancelaciones en el numerador y el denominador de Gc (s) y Gp (s), entonces aunque se han conseguido los resultados deseados de ausencia de interacciones entre una entrada y varias salidas, se debe analizar cuando se producen perturbaciones en el sistema por fuerzas externas, porque el sistema podría hacerse "incontrolable" por dichas cancelaciones.

Por otro lado, al aplicar el algoritmo computacional propuesto en la sección III, se obtiene el compensador serie GC de la siguiente manera:

COMPENSADOR SERIE GC

Compensador PID (1,1)

Grado:-1 1.000

Grado: 0 2.000

Compensador PID (2,1)

Grado:-1 -1.000

Grado: 0 -3.000

Grado: 1 -2.000

Compensador PID (1,2)

Grado (0): 0 *No hay compensador

Compensador PID (2,2)

Grado:-1 0.200

Grado: 0 0.200

El resultado del programa computacional propuesto muestra la matriz del compensador serie GC por columnas, de la siguiente forma: gc₁₁(s), gc₂₁(s), gc₁₂(s) y gc₂₂(s); donde cada elemento es un polinomio en el dominio s que se le aproxima a un controlador PID, debido a que el objetivo de este método de desacoplamiento es tener un controlador que se implemente mediante un control Proporcional, Integral y Derivativo. Este resultado del compensador serie GC expresado en forma matricial, sería:

Al comparar las matrices (6) y (7), se puede comprobar que existe correspondencia entre el cálculo de la solución del método matemático y el resultado que se obtiene con el algoritmo propuesto. Se debe tener en cuenta que el programa computacional propuesto muestra los datos en punto flotante, con tres cifras decimales.

Por último, se debe tener en cuenta cuando un elemento de la matriz del compensador G _C puede ser inadecuado, debido a que no se ajusta a un controlador PID, ya que el grado del numerador es mucho menor al grado del denominador, en dos o más; por lo que el programa computacional mostrará el mensaje "No hay aproximación". También, hay que tener en cuenta cuando un elemento de la matriz G _C puede ser cero, lo que implica que no existe compensador, el mensaje que mostrará el programa es "No hay compensador". Además, el programa mostrará el mensaje "ERROR está mal dada la matriz diagonal G _d ", cuando la matriz diagonal G _d es singular y uno de sus elementos es igual a cero.

Conclusiones

Para darle significado físico al resultado del compensador serie GC, cada elemento de la matriz es aproximado a un controlador PID, y debido a que las ecuaciones descritas son muy simples para desacoplar un sistema, permiten una fácil resolución algebraica para un sistema de dos entradas y dos salidas; sin embargo, ya que el proceso analítico es algebraico, el mismo que se puede alargar y complicar, a la vez que se aumente el número de entradas, salidas y el orden del sistema; por lo que se hace necesario el contar con un algoritmo computacional como el propuesto. Esta técnica de desacoplamiento mediante un algoritmo computacional, solo sirve para sistemas lineales invariantes en el tiempo.

Cabe indicar que existen otros métodos de desacoplamiento de sistemas MIMO, tales como: realimentación de estado y realimentación de salida; los cuales serán presentados en próximos artículos.