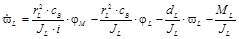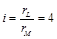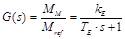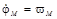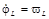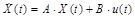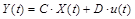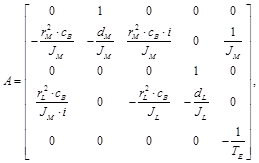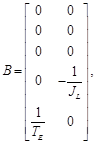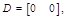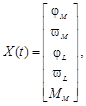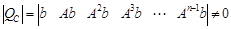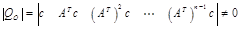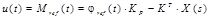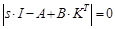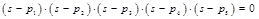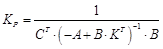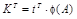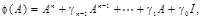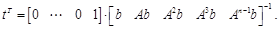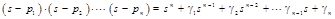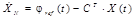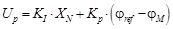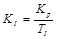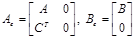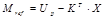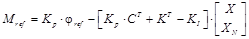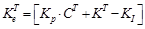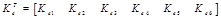Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Los sistemas de control se aplican en varios campos de la ingeniería como por ejemplo en ingeniería automotriz, aeroespacial, eléctrica, mecánica, hidráulica, etc. En este trabajo se aplica controladores a un sistema electromecánico que consiste en un motor de DC con dos masas, la primera masa está conectada al eje del motor y la segunda masa recibe el torque del motor a través de una banda.
Los sistemas de control en variables de estado caracterizan la configuración dinámica del sistema mediante la entrega de datos del estado actual de cada variable del sistema, el control mediante variables de estado se realiza a través de la realimentación de las variables de estado, por lo cual es necesario que estas variables sean medibles y disponibles para la realimentación de sus estados, de modo que aporten información del comportamiento dinámico del sistema.
En (Meah, 2007) presenta un controlador de velocidad para un motor de DC, el objetivo de (Meah, 2007) es presentar un procedimiento para realizar un control de velocidad mediante la plataforma dSPACE y Matlab; realiza una comparación entre los resultados simulados y los resultados medidos sobre el hardware. Del mismo modo que en (Meah, 2007) en este trabajo se utiliza una plataforma dSPACE y se realiza una comparación entre las pruebas realizadas sobre el sistema simulado y sobre el hardware. En este caso se implementa controladores para la posición angular del motor.
En (Manwong, 2008) presenta un controlador de velocidad para un motor de DC, con realimentación de las variables de estados y observador de estados, el controlador incorpora un integrador. En el presente trabajo dos de los controladores aplicados sobre el motor de DC son implementados mediante técnicas de realimentación de estados, y uno de ellos incorpora un control proporcional integral, pero a diferencia de (Manwong, 2008), se aplica control de posición en lugar de velocidad, y no se incluye observadores.
En (Shu, 2007) presenta un método de desarrollo rápido para controlar un motor de DC sin escobillas, en este artículo presenta principalmente el beneficio en cuanto a reducción de tiempo de desarrollo al utilizar la plataforma dSPACE y su comunicación con Matlab. Al igual que en (Shu, 2007) en este trabajo se utiliza la herramienta de software en tiempo real ControlDesk y un módulo dSPACE para la verificación y pruebas de los controladores diseñados.
En (He, 2010) presenta un controlador proporcional integral derivativo PID adaptativo para un motor de DC, el controlador es implementado en un módulo dSPACE. A diferencia de (He, 2010), en este trabajo se ha implementado un controlador PID simple, calibrado por dos métodos experimentales indicados en las siguientes secciones.
En este artículo se resume la implementación de tres controladores aplicados a un sistema electromecánico. Los controladores fueron diseñados con diferentes requerimientos para la posición angular del motor, por lo cual la función escalón de referencia tiene diferente amplitud en cada experimento. En este trabajo se presenta los resultados obtenidos de tres controladores implementados en un mismo hardware como experimentos independientes. Sin embargo se realiza una comparación entre los controladores, pero al no tener la misma amplitud de entrada no se concluye cual tiene el mejor rendimiento, pues los controladores no operan bajo las mismas condiciones.
Se realiza el diseño e implementación de tres controladores, un PID y dos controladores en variables de estado, el primero es un controlador con realimentación de variables de estado “state variable feedback” SVF y el segundo un controlador SVF que incluye un control proporcional integral PI.
Modelamiento de la Planta
Para diseñar los controladores se ha realizado previamente la identificación del sistema a través del uso de la herramienta System Identification Toolbox de Matlab, el cual permite construir el modelo matemático del sistema a través de las medidas de los datos de entrada y salida. El sistema contiene la parte mecánica y eléctrica. El sistema mecánico consta del eje del motor con dos masas, una en el lado del motor y la otra en el lado de la carga; las dos masas están conectadas entre sí mediante una banda que transfiere el torque del motor desde una masa a la otra. Se identificaron las inercias de cada masa, el coeficiente de amortiguamiento viscoso y la elasticidad de la banda. El sistema eléctrico corresponde al motor y al controlador del motor. Una vez realizada la identificación de la planta se la representa en variables de estado, y sobre este modelo matemático se basa los diseños de los controladores.
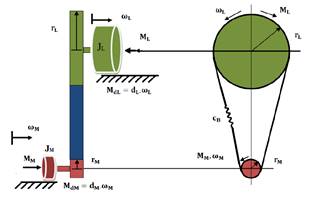
La Fig. 1 presenta los elementos de la parte mecánica del sistema, los cuales son las inercias de las dos masas, el coeficiente de rozamiento de cada inercia y el coeficiente de elasticidad de la banda que conecta las dos masas, en este modelo no se considera el rozamiento de la banda debido a que es mucho menor que el de las masas.
En la Tabla 1, se presenta las abreviaturas de los parámetros del sistema que se utilizan en la modelación del sistema.
TABLA 1 ABREVIATURAS DE LOS PARÁMETROS DEL SISTEMA (Palacios, 2010)
| Abreviatura | Significado |
|---|---|
| ϕ M | Posición angular en el lado del motor. |
| ϕ L | Posición angular en el lado de la carga. |
| ω M | Velocidad angular en el lado del motor |
| ω L | Velocidad angular en el lado de la carga |
| M M | Torque actual del motor |
| M L | Torque en la carga |
| M ref | Torque de referencia |
| c B | Coeficiente de elasticidad de la banda |
| d M | Coeficiente de amortiguamiento en el lado del motor |
| d L | Coeficiente de amortiguamiento en el lado de la carga |
| i | Relación de radios de las dos masas |
| J M | Momento de inercia en el lado del motor |
| J L | Momento de inercia en el lado de la carga |
| T E | Constante eléctrica de tiempo |
| r M | Radio de la masa en el lado del motor |
| r L | Radio de la masa en el lado de la carga |
La aceleración angular en el lado del motor está dada por (1) y en el lado de la carga por (2). Estas dos ecuaciones son deducidas de la suma de torques y pérdidas mecánicas (Lyshevski, 2008) en el lado del motor y en lado de la carga.
La relación de radios de las masas entre el lado de la carga y el lado del motor es:
La función de transferencia de la parte eléctrica está dada por:
De (4) se obtiene la ecuación que describe la relación entre el torque actual y el torque de referencia:
Las velocidades angulares están dadas por:
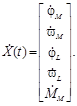
Mediante (1), (2) y de (5) a (7) se tiene la descripción del sistema en variables de estado. En (8) se presenta la ecuación de estado y en (9) la ecuación de salida (Williams & Lawrence, 2007).
Donde:
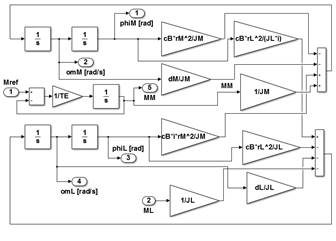
Las entradas del sistema son el torque de referencia y el torque en la carga y la salida es la posición angular en el lado del motor. La Fig. 2 presenta el sistema en diagrama de bloques que utiliza la descripción del sistema en el dominio de la frecuencia mediante el uso de la transformada de Laplace, lo cual se ha realizado para tener la visualización del sistema físico. Se utiliza torque para la entrada del sistema, el torque del motor es proporcional a la corriente de armadura del motor (Kremser, 2013), en este caso por un factor de 0.32 (N/A).
Controlador por Realimentación de Estados
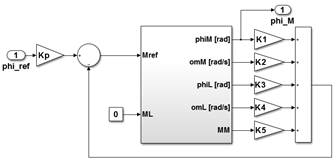
La Fig. 3 presenta un diagrama simplificado de la realimentación en variables de estado. El modelo del sistema es representado por un solo bloque. Las ganancias son asignadas a todas las variables de estado, por lo que para implementar este controlador se tiene sensores que miden las cinco variables de estado. Para realizar el diseño del controlador por realimentación de estados, el sistema debe ser controlable y observable, lo cual se verifica mediante la condición de controlabilidad dada por (10) y de observabilidad dada por (11) (Geering, 2013) .
Al reemplazar (12) en (8) y (9) se tiene la función de transferencia de la planta con el controlador en variables de estado en lazo cerrado dada por (13). Con la función de transferencia se calcula los polos de la planta en lazo cerrado. Se encuentran las ganancias de la realimentación de estados mediante una comparación de los coeficientes del polinomio característico de la planta dada por (15) y la ecuación característica de la función de transferencia dada por (14).
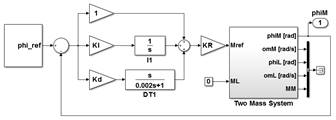
El parámetro K P indicado en la Fig. 3 es un factor necesario para tener una ganancia en estado estable igual a uno. El valor de K P se lo calcula con (16).
Una alternativa en lugar de realizar la comparación de coeficientes es el cálculo de las ganancias mediante la fórmula de Ackermann (Shinners, 1998) dada por (17). La fórmula de Ackermann generalmente se utiliza en sistemas de mayor complejidad, mediante el uso de Matlab esta fórmula permite localizar los polos en las posiciones deseadas.
Donde:
y
Los coeficientes γ i son tales que p1, p2,.. pn sean las raíces del polinomio.
La posición de los polos seleccionados es:
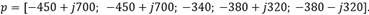Con estos polos se tiene el vector ganancias:
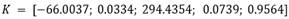y la ganancia del factor K
P
es 7.6052.
Controlador por Realimentación de Estados SVF con Controlador PI Integrado
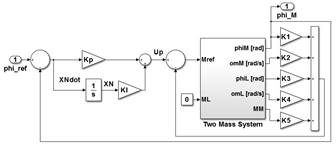
La Fig. 4 presenta el diagrama simplificado del controlador SVF con PI incluido, este tipo de controlador es un sistema servo (Ogata, 2010) que incluye un integrador y un control proporcional. Este controlador tiene un control PI que tiene como entrada la diferencia entre la posición angular del motor y un valor de referencia; la salida del control PI es comparada con la suma de todas las ganancias de realimentación de estados, cuyo resultado es la referencia de torque del sistema.
Este controlador añade una nueva variable de estado al sistema a causa del integrador del PI, esta variable de estado X N está dada por (19).
Al transformar (19) al dominio del tiempo se obtiene:
La salida del controlador PI está dada por:
Al sustituir de (19) a (21) en (8), se tiene la descripción de la dinámica del sistema en variables de estado que incluye la nueva variable XN.
Se definen las matrices extendidas:
En la Fig. 4 se observa que el torque de referencia es función de las ganancias de realimentación de estados, de Up y de las variables de estado.
Al reemplazar (21) en (25) se obtiene:
(25.a)
Donde el vector de ganancias K aparece en (26). Mediante el uso de la fórmula de Ackermann se calcula las ganancias a través de las matrices extendidas y la ubicación deseada de los seis polos, el sexto polo se forma debido a XN. El resultado de la fórmula de Ackermann está dado por (27), el cual debe ser comparado con (26) para obtener las ganancias de realimentación de estado y el coeficiente de integración KI.
Con lo cual se obtiene:
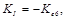
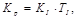
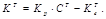La ubicación de los polos de este sistema es:
.
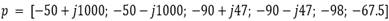De la fórmula de Ackermann se obtiene el vector de ganancias extendidas:
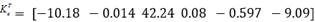. El vector de ganancias K
T
, y las ganancias K
I
y K
p
son:
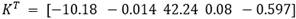, K
I
= 9.0926, K
p
= 0.1346.
Al tener un polo más este sistema se reduce la velocidad del controlador, sin embargo se ha elegido la ubicación de los polos después de varias pruebas y un mejor resultado en el sobre impulso y error en estado estable de la respuesta a la función escalón.
Los resultados del controlador SVF simple y del controlador SVF con PI integrado son comparados con el controlador PID para tener un punto de referencia del comportamiento de los controladores con realimentación de estado. En la siguiente sección se presenta el diseño del controlador PID.
Controlador Proporcional Integral Derivativo
El controlador PID se calibra directamente sobre el motor por medio del método de Ziegler-Nichols, el controlador es presentado en su forma aditiva en la Fig. 5. Para la parte derivativa del controlador PID se utiliza un DT1, el cual contiene un cero y un polo con una constante de tiempo pequeña, esto con el fin de que sea posible su implementación real. Adicional al método de Ziegler-Nichols, también se realiza un ajuste experimental del PID, al variar los parámetros de ganancia y los tiempos de integración sin exceder el 15% del valor de sobre impulso.
Para ajustar el PID por medio de Ziegler-Nichols, se incrementa el valor de ganancia KR desde un pequeño valor hasta que el sistema alcance su límite de estabilidad, en el cual se mide la ganancia crítica KR-critico y el periodo de oscilación Tcritico. Este método permite encontrar en forma experimental las constantes de tiempo del integrador TI y del derivador Td al utilizar la ganancia crítica y el periodo de oscilación, según los valores indicados en la Tabla 2. Se encontró los valores de ganancia crítica y periodo de oscilación crítico: KR-critico = 2 y Tcritico = 0.0658.
TABLA 2 PARÁMETROS DEL PID MEDIANTE ZIEGLER-NICHOLS (Palacios, 2010)
| Parámetro | Valor | |
|---|---|---|
| Ganacia del controlador K R | 0.45 K R-critica | 0.9 |
| Constante de tiempo del integrador TI | 0.5 T critico | 0.0329 |
| Constante de tiempo del derivador Td | 0.125 T critico | 0.008225 |
Procedimiento e implementación
Los controladores son simulados en Matlab y luego cargados en un módulo controlador dSPACE. A través del Interfaz en tiempo real RTI se pueden configurar las entradas y salidas del controlador gráficamente en Simulink (Meah, 2007). La plataforma dSPACE principalmente se utilizan para realizar pruebas en prototipos.
En este trabajo se ha implementado dos controladores SVF y un PID y comparado su desempeño en cuanto a tiempo de establecimiento, sobre impulso y error en estado estable. En este trabajo se realizan las pruebas sobre: 1) El motor físico y 2) La planta o modelo matemático del sistema a controlar. Se ha diseñado e implementado los controladores: PID, control por realimentación de estados SVF simple y control por realimentación de estados con control proporcional integral en la realimentación SVF-PI.
Pruebas Realizadas y Análisis de Resultados
Se realizan pruebas de funcionamiento de los tres controladores: 1) Controlador PID ajustado por Ziegler-Nichols y PID ajustado experimentalmente por prueba y error para limitar el sobre impulso, 2) Controlador SVF simple y 3) Controlador SVF con control PI integrado. Para los tres controladores se aplica una función paso y se mide el tiempo de establecimiento, el error en estado estable y el sobre impulso o sobrecarga. Las tres medidas son realizadas en el lado del motor. Para cada uno de los controladores se presentan dos figuras: posición angular y torque actual, tanto para el motor como para la planta.
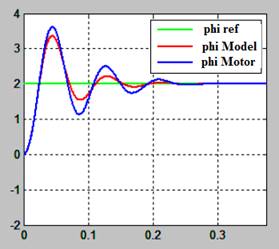
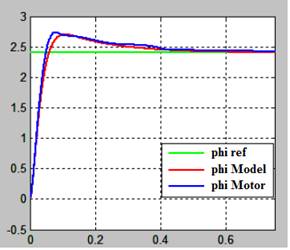
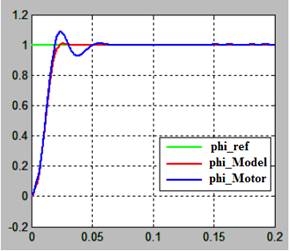
Posición angular: Contiene la gráfica de tres señales de la posición angular, la línea verde presenta la señal de referencia dada por la función paso, la línea roja corresponde al modelo matemático y la línea azul corresponde al motor físico.
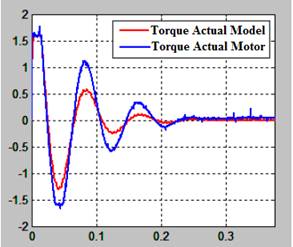
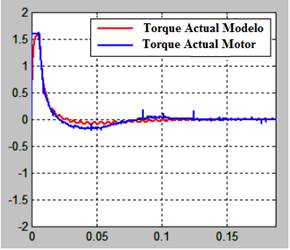
Torque actual: Contiene la gráfica de dos señales, la línea roja es el torque actual del modelo matemático y la línea azul es el torque actual del motor físico.
Las gráficas son realizadas mediante el software ControlDesk de la plataforma dSPACE.
Prueba de Funcionamiento del Controlador PID
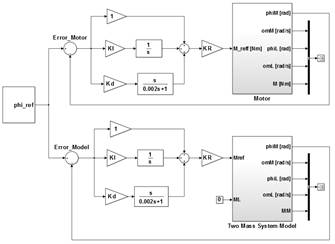
El controlador PID es ajustado 1) a través de la técnica de Ziegler-Nichols y 2) en forma experimental al variar sus parámetros mediante prueba y error. La Fig. 6 presenta el controlador PID sobre la planta y sobre el motor de DC. La función paso se aplica tanto al modelo matemático como al motor físico con el mismo nodo de conexión.
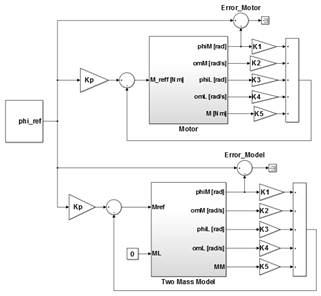
El bloque superior de la Fig. 6 enmascara las señales de entrada y salida, correspondientes a las variables de estado del sistema medidas en el motor; mientras que el bloque inferior de la Fig. 6 presenta al controlador PID aplicado sobre la planta del motor con dos masas. La única variable de estado que se utilizan en el control PID es la posición angular de salida en el lado del motor.
La Fig. 7 presenta la respuesta a la función paso del PID sintonizado con el método de Ziegler-Nichols.
La Tabla 3 contiene los resultados de la respuesta a la función paso para el motor y para la planta cuando se utiliza el controlador PID calibrado por Ziegler-Nichols. Debido a que es un controlador PID, la parte integral del controlador mantiene el error en estado estable en un valor prácticamente igual a cero pero el sobre impulso es bastante alto en el motor y la planta. El tiempo de establecimiento es de 0.29 segundos para el motor físico y 0.33 segundos para la planta simulada.
TABLA 3 RESULTADOS DEL CONTROLADOR PID POR ZIEGLER-NICHOLS (Palacios, 2010)
| Parámetro | Motor | Planta |
|---|---|---|
| Tiempo de establecimiento en segundos | 0.29 | 0.33 |
| Error en estado estable | 0.013% | 0.001% |
| Sobre impulso | 80.81% | 68.55% |
La Fig. 8 presenta el torque actual en el motor y en la planta. El torque en el motor tiene un valor más alto que el torque de la planta, pero no puede exceder 1.6 N, porque el motor dispone de un limitador de corriente para protección, lo cual limita la magnitud de torque aplicado.
Se calibra el controlador PID de la Fig. 6 en forma experimental mediante la variación de sus parámetros y al considerar no exceder el sobre impulso de 15%. Los resultados de esta calibración experimental en base a prueba y error se presentan en la Tabla IV. Se obtiene un sobre impulso 13.97% para el motor, lo cual es una reducción muy alta respecto al valor de 80.81% que se obtiene con Ziegler-Nichols. Sin embargo en este caso el tiempo de establecimiento es mucho más alto con un valor de 0.75 segundos lo cual es más del doble del valor obtenido con Ziegler-Nichols. El error en estado estable es bajo en ambos casos debido al integrador del controlador. Los datos de la Tabla IV se visualizan en la Fig. 9.
Los datos de la Tabla 4 para el motor y la planta son bastante similares en cuanto a tiempo de establecimiento y sobre impulso.
TABLA 4 RESULTADOS DEL CONTROLADOR PID EXPERIMENTAL (Palacios, 2010).
| Parámetro | Motor | Planta |
|---|---|---|
| Tiempo de establecimiento en segundos | 0.75 | 0.73 |
| Error en estado estable | 0.047% | 0.015% |
| Sobre impulso | 13.97% | 12.81% |
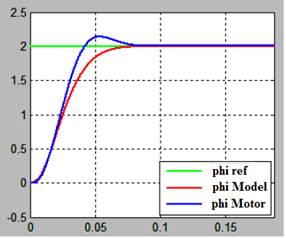
La Fig. 9 presenta la respuesta a la función paso del sistema con controlador PID ajustado experimentalmente, en la cual se observa una reducción significativa del sobre impulso y aumento del tiempo de establecimiento respecto al método de Ziegler-Nichols. La respuesta a la función paso es bastante similar para la planta y el motor.
La Fig. 10 presenta el torque actual del motor y de la planta con el ajuste experimental del PID, como se observa en la Fig. 10 el torque decrece sin oscilaciones del mismo modo que la respuesta a la función paso, la cual también tiene un sobre impulso bajo y sin oscilaciones. El torque actual en la planta y en el motor es bastante similar.
Prueba de Funcionamiento del Controlador SVF Simple
El controlador con realimentación de estados SVF se presenta en la Fig. 11. De igual modo que en el caso del PID se realizan las pruebas sobre la planta y sobre el motor de DC con dos masas. El bloque superior de la Fig. 11 enmascara las señales de salida y de entrada, correspondientes a las variables de estado medidas en el motor, mientras que el bloque inferior de la Fig. 11 contiene el modelo matemático del motor. Las magnitudes de las ganancias de realimentación de estados son las mismas para la planta y para el motor.
La Tabla 5 presenta los resultados de la respuesta a la función paso con el controlador SVF. El sobre impulso con este controlador y el tiempo de establecimiento es mucho menor que con el controlador PID.
TABLA 5 RESULTADOS DEL CONTROLADOR SVF SIMPLE (Palacios, 2010)
| Parámetro | Motor | Planta |
|---|---|---|
| Tiempo de establecimiento en segundos | 0.063 | 0.035 |
| Error en estado estable | 0.028% | 0% |
| Sobre impulso | 8.73% | 0.1% |
La Fig. 12 presenta la respuesta a la función paso por medio del controlador SVF sobre el motor y sobre la planta. En el modelo matemático no se tiene sobre impulso pero al aplicar la misma función paso sobre el motor real, se tiene un sobre impulso del 8.73%.
La Fig. 13 presenta el torque actual sobre la planta y el motor con un controlador SVF. El torque del motor es limitado por el elemento de protección que satura la corriente que alimenta al motor, para no exceder el torque máximo de 1.6 N.
Prueba de Funcionamiento del Controlador SVF con controlador PI integrado
El controlador con realimentación de estados SVF y controlador PI integrado se presenta en la Fig. 14. Se realizan las pruebas sobre la panta y sobre el motor de DC con dos masas. El bloque superior de la Fig. 14 enmascara las señales de salida y de entrada, correspondientes a las variables de estado medidas en el motor; mientras que el bloque inferior de la Fig. 14 contiene el modelo matemático del motor. Los valores de las ganancias de realimentación de estados son las mismas para la planta y para el motor. El controlador PI recibe la señal de error entre la referencia del motor y la posición angular del motor. El torque de referencia para el motor se calcula mediante la diferencia entre la salida del PI y las variables de estado multiplicadas por sus respectivas ganancias de realimentación, como se indica en la Fig. 14.
La Tabla 6 presenta los resultados de la respuesta a la función paso para el motor y para la planta con su respectivo controlador SVF-PI. El sobre impulso con este controlador para el motor es de 6.97% y el tiempo de establecimiento con este controlador es 0.08 segundos, lo cual es mucho menor que con el controlador PID.
TABLA 6 RESULTADOS DEL CONTROLADOR SVF CON CONTROLADOR PI (Palacios, 2010)
| Parámetro | Motor | Planta |
|---|---|---|
| Tiempo de establecimiento en segundos | 0.080 | 0.075 |
| Error en estado estable | 0.003% | 0% |
| Sobre impulso | 6.97% | 0% |
La Fig. 15 presenta la respuesta a la función paso al aplicar el controlador SVF-PI sobre el motor y sobre la planta. En la planta no existe sobre impulso pero al aplicar la función paso sobre motor físico, se tiene un sobre impulso del 6.97%. Con el controlador SVF-PI el error en estado estable es prácticamente cero, esto debido al integrador en lazo cerrado que elimina el error. El tiempo de establecimiento es de 0.08 segundos, lo cual es ligeramente más lento que el SVF simple que tiene un tiempo de establecimiento de 0.063 segundos.
La Fig. 16 presenta el torque actual sobre la planta y el motor con un controlador SVF-PI. Para esta magnitud de torque en el motor no se activa la saturación por torque, debido a que el valor del torque actual es inferior al máximo torque del motor. El torque pico en la Fig. 16 es 1.4 N, mientras que el torque máximo es 1.6 N.
Comparación de Resultados
Los controladores implementados han sido realizados independientemente, con requerimientos diferentes de la amplitud de la posición angular del motor, son experimentos separados. Por lo tanto la comparación de resultados solo indica una aproximación de la tendencia en los resultados. No se puede concluir que se obtendrá los mismos resultados para condiciones iguales en la señal de referencia. Para una comparación que defina el mejor rendimiento entre estos controladores se debe realizar pruebas adicionales con la misma referencia.
La Tabla 7 y Tabla 8 agrupan los resultados obtenidos con los tres controladores PID, SVF y SVF-PI; en estas tablas los títulos PID 1 corresponde a los resultados con el controlador PID ajustado por Ziegler-Nichols y PID 2 corresponde a los resultados con el PID ajustado experimentalmente mediante prueba y error.
La Tabla VII presenta los resultados para las pruebas sobre el motor físico, en la cual se observa que el menor tiempo de establecimiento se logra con el controlador SVF simple con un valor de 0.063 segundos, seguido por el controlador SVF-PI con un valor de 0.08 segundos. El PID tiene un tiempo de establecimiento mucho más lento, cuyo valor es de 0.29 segundos con la calibración por Ziegler-Nichols y de 0.75 segundos para la calibración mediante prueba y error.
El menor error en estado estable se obtiene con el controlador SFV- PI y después con el controlador PID. Tanto el PID como el SVF-PI tienen menor error en estado estable que el SVF, debido a que disponen de un integrador en el lazo de realimentación.
El menor sobre impulso se obtiene con el SVF-PI con un valor de 6.97% y segundo con el controlador SVF simple con un valor de 8.73%. Al utilizar la técnica de calibración de Ziegler-Nichols, el PID tiene un sobre impulso muy alto de 80.81%, sin embargo con la calibración experimental del PID mediante prueba y error, se obtuvo mejores resultados con un valor de 13.97%; pero el tiempo de establecimiento aumentó a 0.75 segundos.
TABLA 7 RESULTADOS DE LOS CONTROLADORES SOBRE EL MOTOR (Palacios, 2010)
| Parámetro | PID 1 | PID 2 | SVF | SVF -PI |
|---|---|---|---|---|
| Tiempo de establecimientoENT#091;sENT#093; | 0.29 | 0.75 | 0.063 | 0.080 |
| Error en estado estable | 0.013% | 0.047% | 0.028% | 0.003% |
| Sobre impulso | 80.81% | 13.97% | 8.73% | 6.97% |
La Tabla Tabla 8 presenta los resultados de las pruebas sobre la planta o modelo matemático del motor.
TABLA 8 RESULTADOS DE LOS CONTROLADORES SOBRE LA PLANTA (Palacios, 2010)
| Parámetro | PID 1 | PID 2 | SVF | SVF -PI |
|---|---|---|---|---|
| Tiempo de establecimiento ENT#091;sENT#093; | 0.33 | 0.73 | 0.035 | 0.075 |
| Error en estado estable | 0.001% | 0.015 | 0% | 0% |
| Sobre impulso | 68.55% | 12.81 | 0.1% | 0% |
Al igual que con el motor, el menor tiempo de establecimiento se logra con el controlador SVF, el menor sobre impulso con el SVF-PI y el menor error en estado estable es cero con los controladores SVF y cercano a cero con el PID 1. Sin embargo la planta es una aproximación matemática del motor físico por lo que existe cierta diferencia en los resultados especialmente en el de sobre impulso.
Conclusiones
Los resultados indican que los controladores con realimentación de variables de estado SVF tienen un tiempo de establecimiento mucho menor que los controladores PID. El sobre impulso de los controladores SVF es significativamente menor que el obtenido con los controladores PID. Los controladores SVF y SVF-PI solo pueden implementarse si se dispone de la realimentación de todas las variables de estado, si se requiere realizar un controlador SVF y no se dispone de todas las variables de estado, existe la alternativa de implementar un controlador con observadores de estado para las variables que no se pueden medir. Se ha obtenido mejores resultados en sobre impulso con el método experimental de prueba y error que con el método de Ziegler-Nichols, debido a que el método de Ziegler-Nichols se basa en el estudio experimental de múltiples respuestas de sistemas para definir las ganancias del PID, mientras que la calibración experimental del PID mediante prueba y error se ha realizado específicamente para este sistema electromecánico.
