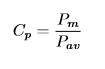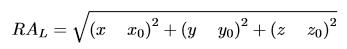I. INTRODUCCIÓN
Las lámparas de descarga de alta intensidad de haluros metálicos (HID-MH) son muy empleadas en aplicaciones de iluminación; especialmente en ambientes exteriores, debido a que presentan características de alta eficiencia (lm/) 1), (2), ya que basan su funcionamiento en la radiación de energía a temperaturas superiores en relación a las lámparas incandescentes. Presentan, además, muy buena reproducción de color, lo que las hace idóneas para aplicaciones donde esta característica es crítica. Sin embargo, su comportamiento no lineal en el transcurso del tiempo y la variación caótica de sus parámetros físicos proveen un comportamiento no deseable en la presión interna del tubo de descarga, lo que a su vez puede ocasionar una interrupción del arco eléctrico y en consecuencia un posible fallo en su funcionamiento. A este fenómeno se lo conoce como resonancia acústica (RA), que se manifiesta visualmente como una deformación en la trayectoria del arco dentro del tubo de descarga 3. El surgimiento de la RA, depende de varios factores, entre ellos la geometría del tubo de descarga, presión del gas de llenado, dispersión de la manufactura, potencia de la lámpara, temperatura de operación, frecuencia de operación y modos propios de RA de la cavidad, siendo que algunos de estos parámetros son cambiantes en el tiempo 4. El conocimiento del comportamiento dinámico de los parámetros representativos de la lámpara posibilitaría el diseño y posterior desarrollo de un balasto electrónico orientado a la operación estable de este tipo de luminarias. Por lo expuesto, es necesario detectar la presencia de RA. En este sentido, básicamente existen tres métodos de detección de RA: medición de las emisiones acústicas, eléctricamente al medir la impedancia equivalente de la lámpara y óptica al detectar desplazamientos o perturbaciones en el arco de descarga 5. En este trabajo se emplea una mezcla de los dos últimos métodos.
Además, se presenta un análisis del comportamiento de las variables de operación significativas de la lámpara a diferentes frecuencias. Finalmente, se plantea una técnica de reconstrucción del arco de descarga en 3D al considerar fotografías ortogonales del arco y a partir de esta se propone un método que permite cuantificar la amplitud de la resonancia acústica longitudinal.
II. DISEÑO DEL EXPERIMENTO
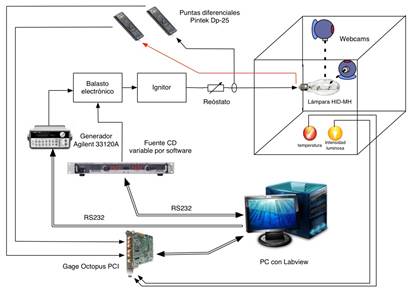
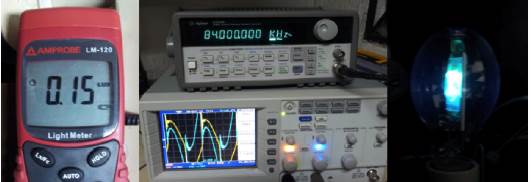
El esquema de experimentación empleado para obtener datos de las variables físicas y eléctricas de las lámparas HIDMH se presenta en la Figura 1, que es una adaptación del propuesto por 5. Se parte de un balasto electrónico que consiste de un inversor en conFiguración puente completo, el mismo que es alimentado por una fuente de corriente directa Kepko KLP600 cuya tensión de salida es variable por software. Las señales de conmutación de los mosfets IRF740 empleados en el inversor son suministradas mediante un driver IR2130 al que se le entrega una señal de onda cuadrada de alta frecuencia en el rango de 10 a 50 kHz proveniente del generador de señales Agilent 33120A, también controlado vía software. A este esquema se añade un ignitor tipo serie que es conectado y desconectado de la lámpara mediante un relé conforme se lo requiera. En el habitáculo donde se encuentra la lámpara existen dispuestas ortogonalmente dos cámaras web Genius iLook300 de 8 Mpixels protegidas mediante el empleo de filtros ópticos de densidad neutra y ganancia 1/1024, un sensor de intensidad luminosa DC-SS012V100 y una termocupla tipo K. La lámpara se encuentra en serie con un reóstato Terco de 1700W que se emplea como limitador de corriente debido a la característica de impedancia negativa de este tipo de lámparas 6. Para capturar las formas de onda de la tensión y corriente en la lámpara (esta última indirectamente tomada al medir la tensión en el reóstato), se emplearon puntas diferenciales Pintek DP-25 con una atenuación de 200. Las señales atenuadas de tensión y corriente se introducen en conjunto con las señales de los sensores de temperatura e intensidad luminosa a una tarjeta de adquisición de datos PCI modelo Gage Octopus de 250Ms/s.
Tanto el generador Agilent como la fuente DC kepko son controladas vía RS232 opto-aislado por un computador. El programa que automatiza la toma de datos de tensión, corriente, intensidad luminosa, temperatura, frecuencia de operación, las capturas de las imágenes provenientes de las cámaras web y el control de los instrumentos fue desarrollado en LabView 2012.
Las señales de tensión y corriente capturadas son procesadas en el computador para obtener su valor eficaz y así disponer de los valores que se presentan en la tabla I. Las imágenes ortogonales del arco de descarga son procesadas mediante un script realizado en Matlab que en base al estándar de iluminación monocromática del Comité Nacional del Sistema de Televisión 7, dado por (1) permite la conversión de la imagen capturada en formato RGB a una escala de grises.
Tabla I: Ejemplo de datos obtenidos
| Temperatura | Intensidad Luminosa | Voltage Ch2 | Voltage Ch1 | Potencia | Frecuencia |
|---|---|---|---|---|---|
| C | Lux | Vrms | Vrms | Wrms | Hz |
| 22,16 | 15700,00 | 112,00 | 145,80 | 175,59 | 10000,00 |
| 22,10 | 15400,00 | 115,40 | 174,60 | 216,65 | 15000,00 |
| 22,21 | 14800,00 | 114,40 | 185,00 | 227,57 | 20000,00 |
| 21,98 | 14000,00 | 111,80 | 165,80 | 199,32 | 25000,00 |
| 22,25 | 13220,00 | 111,20 | 170,00 | 203,27 | 30000,00 |
| 22,46 | 12810,00 | 112,60 | 188,00 | 227,62 | 35000,00 |
| 22,17 | 12400,00 | 111,20 | 193,20 | 231,01 | 40000,00 |
| 22,10 | 11870,00 | 113,80 | 186,80 | 228,58 | 45000,00 |
| 22,18 | 11250,00 | 111,80 | 202,00 | 242,83 | 50000,00 |
Donde Y es la luminancia monocromática y R,G y B son respectivamente las luminancias de los canales rojo, verde y azul. Una vez convertida la imagen en escala de grises se procede a binarizar la imagen de tal manera que se obtenga un uno donde exista un gris y un cero donde exista un blanco, así se obtiene una matriz de unos y ceros que representa el contorno del arco de descarga. A esta matriz mediante un escaneo fila-columna se procede a identificar la ubicación en coordenadas (x,y,z) de los pixeles correspondientes a un uno, obteniéndose el borde del arco de descarga. Para determinar las coordenadas del eje del arco de descarga se procede a determinar el punto medio entre los bordes de una columna de la matriz de la imagen. El mismo procedimiento se aplica a la imagen de la cámara ortogonal. En el procesamiento las dos imágenes tienen la misma dimensión de 1280x1024 pixels, además físicamente se han colocado las dos cámaras a la misma distancia respecto del eje entre los electrodos de la lámpara para evitar distorsiones en las imágenes.
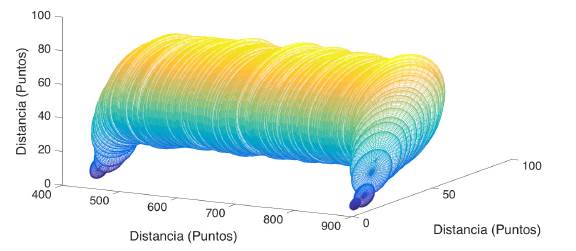
Para la reconstrucción del arco de descarga en 3D se procedió a definir cada punto del eje del arco en sus tres coordenadas rectangulares, este punto se constituirá en el centro de una elipse que pasa por los cuatro puntos correspondientes a los bordes del arco, la misma operación se repite para todos los puntos del eje del arco de descarga como se muestra en la Figura 2.
III. RESULTADOS
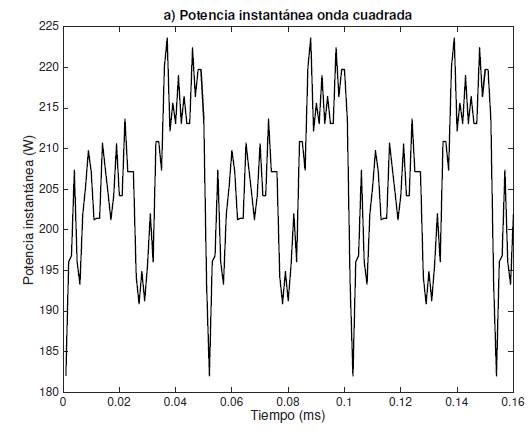
Al alimentar la lámpara con una onda cuadrada en tensión, se obtiene una potencia constante 8 como se puede observar en la Figura 3, que resulta del producto punto a punto de la tensión y la corriente.
La potencia no es modulada por ninguna frecuencia y es similar a la potencia que se entregaría por una fuente constante (CD), por ello la lámpara es inmune al problema de la RA 9 y, además la frecuencia de operación no es importante en estas condiciones, exceptuando las consideraciones de pérdidas por conducción y conmutación en los semiconductores.
Sin embargo, como se ha mencionado en 10)-(12 no es posible obtener una onda cuadrada perfecta y en consecuencia la potencia mostraría un rizado (ripple) con posibles cruces por cero, lo que podría llegar a excitar las RA. Por un lado, una manera de determinar el efecto que causa el rizado de la potencia instantánea en la existencia de las resonancias acústicas es el empleo del factor de cresta como se presenta en la ecuación (2).
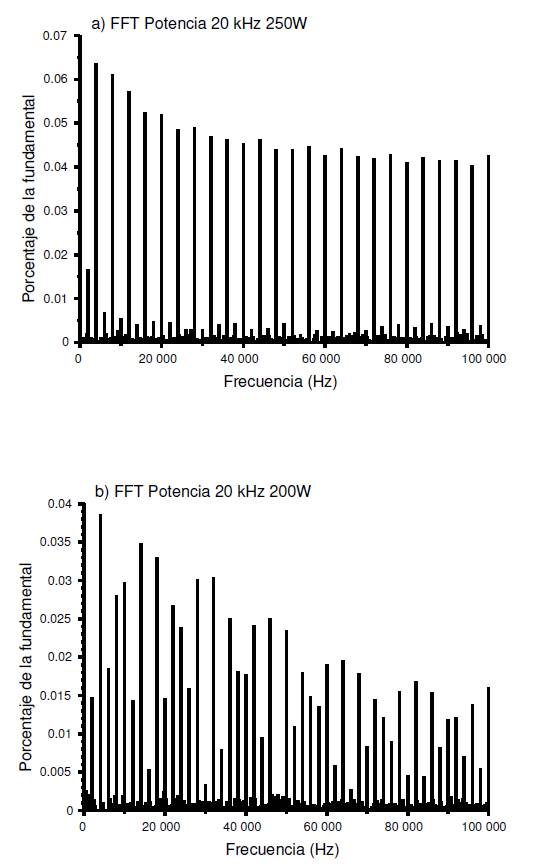
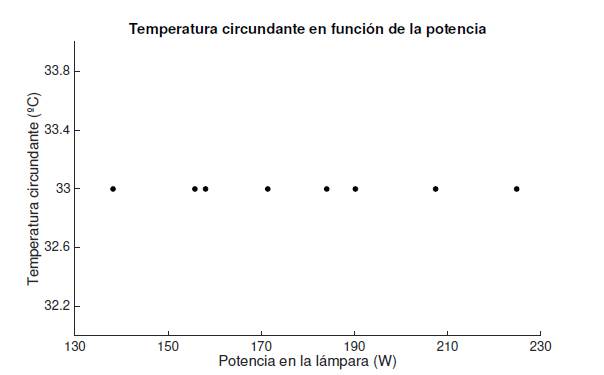
Donde P m es la potencia instantánea máxima y P av define la potencia media en la lámpara. Si el factor de cresta es la unidad, la probabilidad de que aparezca alguna RA es mínima, por otro lado si su valor es mayor a uno y conforme se incremente, las resonancias acústicas existirán y aumentarán 9. Por otro lado, en cuanto a la distribución espectral de potencia en la lámpara presentada en la Figura 4, esta varía considerablemente cuando la potencia media en la lámpara es reducida de su valor nominal (Figura 4a) a un 20% (Figura 4b). Además, se observa que la temperatura al ser una variable lenta no cambia significativamente frente a variaciones de la potencia media de alimentación de la lámpara tal como se muestra en la Figura 5.
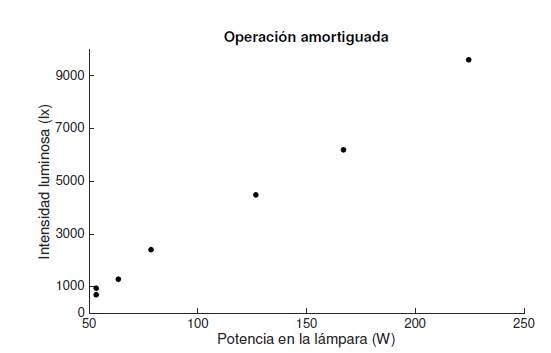
La radiancia luminosa de la lámpara (medida con el sensor ubicado ortogonalmente a 22,3 centímetros del eje entre los electrodos), se incrementa conforme la potencia media aumenta su valor a una frecuencia determinada de funcionamiento (10 kHz).
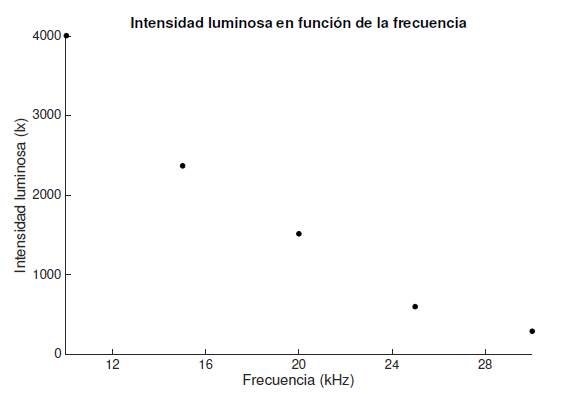
Mientras se observa que la luminancia decae conforme la frecuencia de operación se incrementa (Figura 6). Dentro del rango de frecuencias de análisis (10 kHz-50 kHz) la disminución de la intensidad luminosa fue del 85%.
Para la operación dimerizable 13, se observa que la intensidad luminosa decae considerablemente conforme la frecuencia se incrementa, encontrándose que para la lámpara de prueba (Philips MH/U 250W/640 E40 CL) al 10% de la potencia nominal y con 1,2 lux existe extinción del arco de descarga (Figura 7). La lámpara se encendió a 10 kHz y a potencia nominal, posteriormente se decrementó la potencia hasta llegar a 35 W y 10,5 lux. Se realizó un incremento de frecuencia llegando hasta los 110 kHz, donde la lámpara se apagó al ojo humano (0,1 lux en el luxómetro), sin embargo al disminuir la frecuencia se observó un “reencendido” y un incremento de la intensidad luminosa, parte de este proceso se puede observar en la Figura 8.
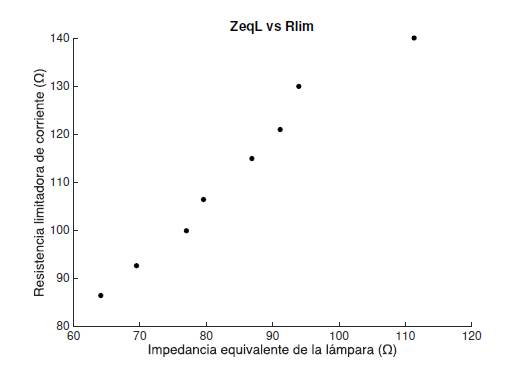
Un comportamiento no reportado en la literatura científica sobre lámparas HID-MH trata sobre la relación de la resistencia que cumple con la función de limitar la corriente (o impedancia limitadora en el caso de tratarse de una bobina) y la resistencia equivalente de la lámpara. Como se puede observar en la Figura 9, se puede afirmar que la relación es directamente proporcional y prácticamente lineal para el rango de frecuencias de operación estudiadas; es decir, mientras la resistencia limitadora aumenta, la resistencia equivalente de la lámpara incrementa su valor de forma lineal con correlación superior a 0,9 (0,9845 para el caso de la Figura 9), y mantiene, prácticamente, la proporción en el divisor de tensión constituido entre la lámpara y la impedancia limitadora de corriente.
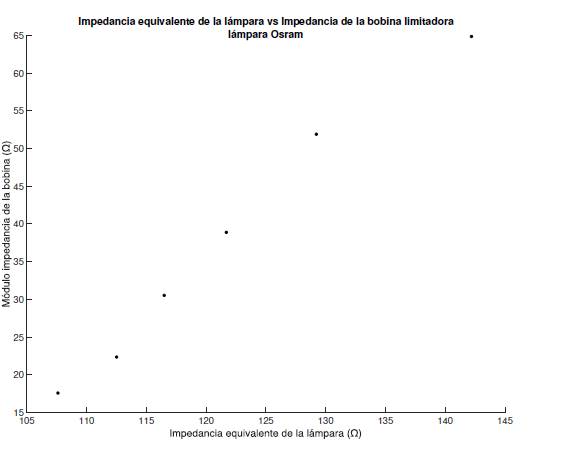
Para determinar el comportamiento de la lámpara, al emplear una bobina, para limitar la corriente se construyó un inductor variable de 118.63 uH a 238.17 uH y 3 A. La frecuencia de operación se mantuvo constante en 20 kHz, y al variar la inductancia en el rango indicado; se observó para las 5 lámparas de prueba que existe una relación proporcional prácticamente lineal entre la impedancia de la bobina que limita la corriente y la impedancia equivalente de la lámpara conforme se puede observar en la Figura 10. Este comportamiento corrobora lo establecido en la Figura 6, ya que al incrementarse la frecuencia, la impedancia de la bobina limitadora de corriente se incrementa y en consecuencia la impedancia de la lámpara, ocasionando un decremento en la corriente, la potencia y la intensidad luminosa. Aspectos que se deben considerar en el proceso de diseño de balastos electrónicos que emplan una impedancia limitadora.
Con el propósito de obtener una generalización respecto al comportamiento de la impedancia equivalente de las lámparas HID-MH, el experimento antes mencionado se ha repetido para diferentes luminarias y cuyo resultado se muestra en la tabla II, donde se puede observar la relación prácticamente lineal entre la impedancia limitadora de corriente y la impedancia instantánea de distintas lámparas.
Tabla II: Comportamiento RL - Zlim
| Phillips 1 | Phillips 2 | Osram | Silvania | ||||
|---|---|---|---|---|---|---|---|
| RL | Zlim | RL | Zlim | RL | Zlim | RL | Zlim |
| 108,1 | 7,454 | 91,69 | 26,41 | 107,6 | 17,60 | 69,94 | 10,18 |
| 113,9 | 14,91 | 92,24 | 29,81 | 112,5 | 22,36 | 113,9 | 29,81 |
| 121,1 | 29,81 | 96,82 | 35,21 | 116,6 | 30,53 | 119,2 | 40,71 |
| 126,6 | 37,27 | 102,7 | 44,89 | 121,7 | 38,91 | 122,3 | 44,01 |
| 131,8 | 50,88 | 112,2 | 59,86 | 129,2 | 51,88 | 130,0 | 51,88 |
| 141,4 | 74,82 | 113,3 | 74,82 | 142,2 | 64,85 | 141,0 | 59,86 |
| correlación=0,9929 | correlación=0,9725 | correlación=0,9930 | correlación=0,9698 | ||||
Para establecer la longitud del arco del modelo tridimensional expuesto en la Figura 2, se realiza un cálculo de distancia entre dos puntos tridimensionales consecutivos (3), igualmente se repite esta operación para todos los puntos del arco de descarga.
Donde RA L es la distancia entre dos puntos tridimensionales del arco de descarga dado por las coordenadas iniciales P 0 (x0,y0,z0) y finales P (x,y,z) obtenidas mediante el método descrito en el algoritmo de la Figura 11. Este cálculo se realiza en forma iterativa y acumulativa a lo largo del arco de descarga para obtener la longitud en pixeles del mismo. Luego, se realiza una relación proporcional entre la longitud del arco en condiciones de operación sin resonancia (longitud mínima del arco de descarga) y la calculada por el método descrito y se procede a normalizar estas magnitudes. La longitud se calcula para diferentes frecuencias de operación con el objetivo de obtener una medida de la deformación del arco de descarga o RA en su modo longitudinal, conforme se presenta en la Figura 12.

Figura 11: Porcentaje de incremento de la longitud del arco de descarga para diferentes frecuencias de operación
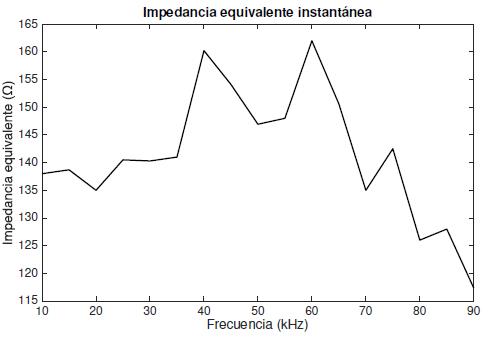
Finalmente, la amplitud de la desviación del arco de descarga, Figura 12, se presenta como una variación porcentual respecto a la longitud nominal del mismo. En la Figura 13 se verifica la validez del método propuesto para determinar la longitud del arco de descarga por medio de la reconstrucción 3D, en contraste al comportamiento de la impedancia equivalente de la lámpara de prueba frente a variaciones en la frecuencia de operación.
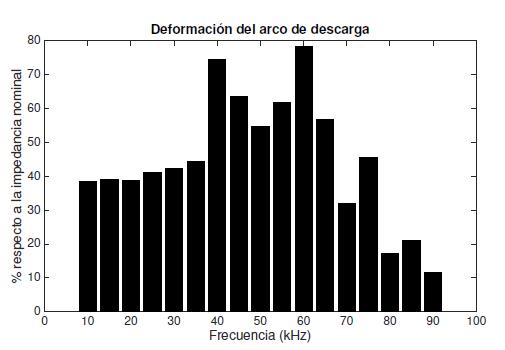
Figura 12: Porcentaje de incremento de la longitud del arco de descarga para diferentes frecuencias de operación
La validación del método propuesto, mediante la correlación entre la longitud del arco de descarga y la impedancia equivalente de la lámpara, se puede observar en la tabla III.
Tabla III: Correlación impedancia medida - impedancia calculada
| Frecuencia Hz | Longitud del arco mm | Resonancia % | Impedancia medida | Impedancia calculada | Error % | |
|---|---|---|---|---|---|---|
| 15 | 48,72 | 39,20% | 138,70 | 138,34 | 0,36% | |
| 20 | 48,55 | 38,71% | 135,00 | 138,71 | 2,75% | |
| 40 | 61,12 | 74,63% | 160,22 | 174,63 | 8,99% | |
| 45 | 57,28 | 63,66% | 154,12 | 163,66 | 6,19% | |
| 50 | 54,17 | 54,77% | 146,93 | 154,77 | 5,34% | |
| 55 | 56,66 | 61,89% | 148,00 | 161,89 | 9,38% | |
| 65 | 54,91 | 56,89% | 150,60 | 156,89 | 4,17% | |
| 70 | 46,17 | 31,91% | 135,00 | 131,91 | -2,29% | |
| 75 | 51,00 | 45,71% | 142,50 | 145,71 | 2,26% | |
| 90 | 39,02 | 11,49% | 117,34 | 111,49 | -4,99% | |
| Correlación impedancia medida - impedancia calculada por el método de reconstrucción del arco en 3D | 0,9851 | |||||
IV. CONCLUSIONES Y FUTUROS TRABAJOS
El empleo de dos cámaras dispuestas ortogonalmente para capturar el arco de descarga permite obtener la información a partir de la que se puede reconstruir el mismo tridimensionalmente. Con esta información es factible el calcular una medida que represente la amplitud de RA en su modo longitudinal.
Al variar el valor de la impedancia serie a la lámpara, se observó un cambio proporcional en la impedancia equivalente de la lámpara y el mantenimiento de la proporción en el divisor de tensión del conjunto lámpara impedancia limitadora.
La temperatura de la lámpara no varía significativamente frente a cambios en la frecuencia de operación en el rango de frecuencias de estudio.
Es posible obtener una operación amortiguada de las lámparas HID-MH incrementando la frecuencia de operación, sin embargo, es discutible la utilidad práctica de obtener una fuente luminosa que consume potencia y no entrega radiación lumínica.
Para medir la RA en sus tres modos (longitudinal, radial y acimutal), en un trabajo futuro se propone realizar una equivalencia respecto al volumen del arco de descarga, en base a la reconstrucción del mismo en tres dimensiones partiendo de fotografías ortogonales en escala de grises y proveyendo de valores a cada tonalidad de gris en cuanto a distancia respecto al eje del arco de descarga.