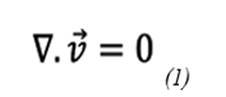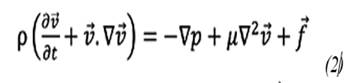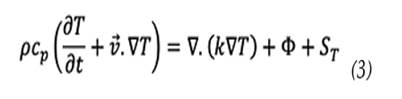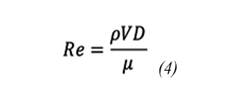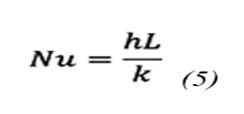I. INTRODUCTION

Heavy crude is characterized by its high density and viscosity. This type of oil is located at the lower end of the classification spectrum according to the API scale, indicating that it is denser and more viscous compared to other types of crude oil (⁽¹⁾. The exploitation and transportation of heavy crude present significant challenges for the oil industry, especially in areas with unique environmental conditions, such as the Ecuadorian east. Due to its high viscosity, heavy crude requires specialized technologies for efficient handling. One of the main challenges is to prevent temperature loss during transport, as this can significantly increase its viscosity and hinder its flow (⁽²⁾). The viscosity of crude oil, which is closely related to its temperature, has a significant impact on both the efficiency and cost of pumping through pipelines. Higher viscosity requires more energy to move the crude oil, thus increasing operational costs (⁽³⁾).

Cazorla et al. (⁽⁴⁾) they investigated the impact on production and recovery factor in ultra-heavy crude reservoirs through the application of electromagnetic waves in horizontal wells. The main objective was to study how electromagnetic heating can contribute to increasing the production of viscous hydrocarbons, specifically in the Orinoco Oil Belt in Venezuela. A numerical simulation was conducted to analyze the behavior of the reservoir and the effectiveness of this technology in reducing crude viscosity, which could lead to significant improvements in the extraction of these resources.

Tolentino et al. (⁽⁵⁾) they implemented a novel technology for heating oil fields using nuclear reaction capsules. A steady-state thermal simulation of an oil field similar to Cerro Negro was conducted using COMSOL Multiphysics software with the Finite Element Method. A nuclear reaction capsule was designed with specific dimensions to heat the porous medium, and 11 capsules were distributed throughout the reservoir to enhance the extraction of heavy and extra-heavy crude oil, thereby demonstrating the viability and effectiveness of this innovative technology.

Ramírez et al. ⁽³⁾ they carried out the prediction of temperature and viscosity profiles in heavy oil production wells by implementing an induction heater at the bottom of the well. The study focuses on the impact of electric heating on the viscosity of heavy oil, with the goal of improving crude mobility and well efficiency. A CFD model was developed to simulate the thermal and viscosity behavior of heavy oil in the well, demonstrating a significant reduction in the dynamic viscosity of the crude with electric heating. The results validate the effectiveness of induction heating in reducing the viscosity of heavy oil, which could have significant implications for oil production in heavy crude wells.

Pinilla et al. ⁽⁶⁾ they conducted a Computational Fluid Dynamics study on water production in mature heavy oil fields with horizontal wells. Numerical experiments were performed based on a complete set of 3D Navier-Stokes equations to simulate multiphase flows in porous media in horizontal heavy oil production wells. A sensitivity analysis was conducted on different rock and fluid properties, such as permeability and oil viscosity, assuming homogeneous porous media. The numerical model was verified with field data using two approaches: one assuming homogeneous rock properties and another using heterogeneous rock properties measured from well logs. The validation results showed that the numerical model could reproduce the observed field production trend with a deviation of 20 % compared to actual data. Additionally, critical hydraulic data in the well, such as pressure and velocity profiles, were obtained, which could be used to enhance production efficiency.

Zhang et al. ⁽⁷⁾ they conducted a three-dimensional numerical simulation to study the heat transfer behavior and flow of waxy crude oil in an inclined pipeline. The main objective was to analyze how the temperature and velocity fields of waxy crude oil vary in pipelines with different inclination angles, providing a theoretical guide for the safe operation of pipelines. Factors such as three-dimensional heat transfer, heat transfer in the surrounding soil, and changes in physical parameters with temperature were considered to develop a more accurate and realistic mathematical model.

Kumar et al. ⁽⁸⁾ they conducted a study using computational fluid dynamics analysis to investigate the flow behavior in the annular core of heat exchangers composed of nanoparticles, specifically employing a heat exchanger made up of nanoparticles. The study focused on the flow of crude oil and water in the annular pipe system, aiming to analyze the heat transfer efficiency, pressure drop, and overall performance of the system. Additionally, the flow characteristics and variations between the crude oil and water were explored, along with the molecular behaviors induced by the central channels. The research also aimed to enhance the understanding of heat generation and fluid flow within the annular core, in order to predict variations in annular flow and improve the control of fluid density within the annular core.

While research has focused on the analysis through CFD simulation of crude oil heating methods, as well as velocity, pressure, and temperature profiles, the heat loss of heavy crude during surface transport has received less attention. This critical aspect of heavy crude handling still requires detailed studies that could significantly improve efficiency in the transport and management of such hydrocarbons. In this context, the current study focuses on the simulation of surface pumping of heavy crude with an API gravity of 17.5, under the specific atmospheric conditions of eastern Ecuador. Using CFD, this research aims to analyze the temperature loss over a 50-meter pipeline section, in addition to determining the convective coefficient at which the fluid loses heat, knowing that the main mechanism by which heavy crude loses temperature is through convection with the environment.

This introduction to the problem and the methodological approach adopted lays the groundwork for a broader discussion on potential solutions and the practical implications of the findings, ultimately aiming to move towards more efficient and economically viable management of heavy crude.

II. MATERIAL AND METHODS

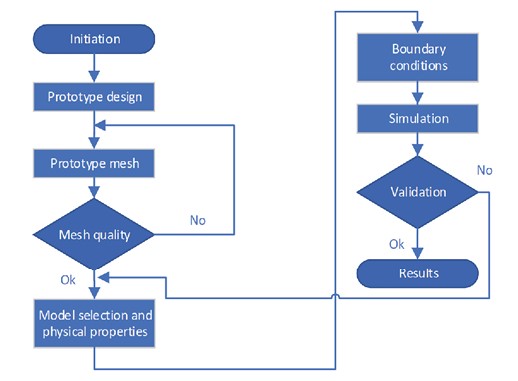
CFD simulation is widely used in the industry due to its multiple advantages, which include lower costs compared to experimental techniques and the ability to simulate complex physical phenomena. However, CFD simulation must be experimentally validated to confirm that the model configurations and parameters are appropriate for the case study ⁽⁹⁾, CFD has been widely used in the study of processes where there is mass and heat transfer in the air ⁽¹⁰⁾,⁽¹¹⁾. (Fig. 1), the methodology used for the CFD simulation can be observed.

The model used in the CFD simulation has the same dimensions as the actual pipeline. InFig. 2, you can see the model used in the simulation.

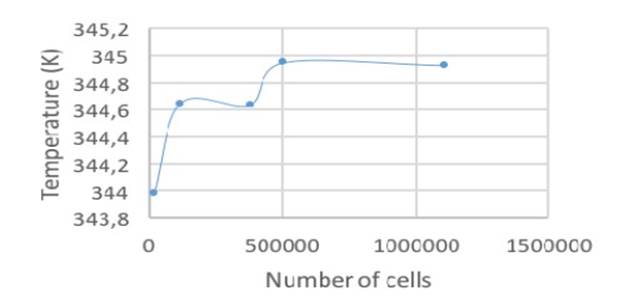
For meshing, Tetrahedron elements are used as can be seen inFig. 3. The Orthogonal Quality metric is used to measure the quality of the mesh ⁽¹³⁾, ⁽¹⁴⁾, in the simulation, 501 800 elements were used; this is the optimal number of elements because, beyond this number, the analyzed variable, which is temperature, stabilizes, as can be observed inFig. 4.

The properties of the pipeline and heavy crude can be seen inTable 1andTable 2, respectively.

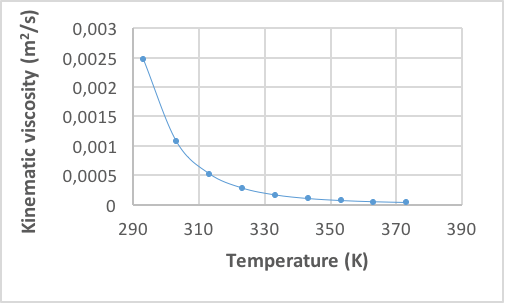
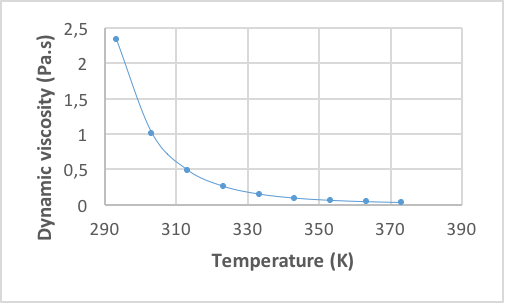
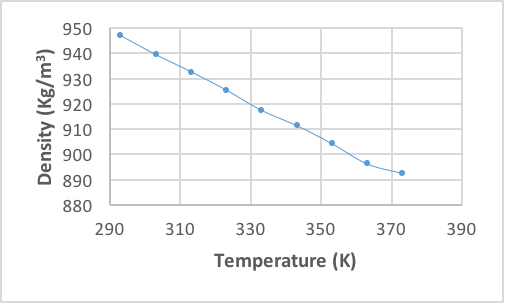
The fluid properties are determined from the curves obtained in the laboratory, which are shown in (Fig.5), (Fig. 6), and (Fig.7). This is done using an average temperature of 347.04 K.

In computational fluid dynamics simulations, phenomena are modeled using mathematical formulas, which are usually partial differential equations. To analyze the surface pumping of heavy crude, the Navier-Stokes equations are used, which describe the movement of fluids. When considering the fluid as incompressible, two fundamental equations are applied: the continuity equation (1), which ensures mass conservation, and the momentum equation (2), which describes the conservation of momentum ⁽¹⁵⁾, ⁽¹⁶⁾.

where ρ is the density of the fluid, v is the velocity field, p is the pressure, µ is the dynamic viscosity of the fluid and 𝒇 are external forces.

To model the heat transfer between the fluid flowing inside the pipeline and the external environment, the fluid is considered incompressible and not involved in chemical reactions. In this context, the heat transfer equation (3) is used, which allows for the calculation of the fluid’s thermal variation in response to environmental conditions and the characteristics of the pipeline.

where 𝑪 𝒑 is the specific heat at constant pressure, T is the temperature, k is the thermal conductivity, ᶲ represents heat generation by viscous dissipation and 𝑺 𝑻 is an additional source term that may include effects such as radiation heat transfer or internal or external heat sources.

The algorithm used for the numerical simulation of the equations is SIMPLE ⁽¹⁷⁾, for the spatial discretization of pressure, the method used is PRESTO ⁽¹⁸⁾, the flow of heavy crude oil through the pipeline is considered laminar since the Reynolds number is less than 2000. The equation used is equation (4).

where V is the velocity and D is the diameter of the pipe.

Given the exposure of the pipe to the environment, it is imperative to determine the convective heat transfer coefficient. For this purpose, the Nusselt number is used, a dimensionless magnitude that quantifies heat transport by convection. The correlation between the Nusselt number and the convective coefficient is established through equation (5):

where Nu is the Nusselt number, h is the convection heat transfer coefficient, L is the length of the pipe and k is the thermal conductivity of the pipe.

The Nusselt number for a flow like this case, which is developed both hydraulically and thermally, is 4.36 ⁽¹⁹⁾, ⁽²⁰⁾.

The boundary conditions used are as follows:

Inlet: the fluid enters at a speed of 0.73043 m/s, due to the analyzed well producing 2225 barrels and the internal diameter of the pipeline being 0.0848 m. The entering temperature is 348.15 K, a data point taken in the field.

Outlet: for simplicity in the simulation and considering that the objective is to calculate the temperature of the fluid at the outlet, it is assumed to be exposed to atmospheric pressure.

Outside of the pipeline: the exterior of the pipeline is exposed to an ambient temperature of 292.15 K.

To obtain temperature data in the field, bimetallic thermometers model E from Ashcroft were used, as shown inFigure 8.

III. RESULTS

For the validation of the simulation, the experimental outlet temperature of 345.93 K and the CFD simulation result of 344.95 K were used. With these values, a Mean Absolute Percentage Error (MAPE) of 0.28 % was obtained. Additionally, to validate the convective coefficient value obtained from the simulation of 52 W/m².K, it was compared with the analytically derived value of 52.9 W/m².K, resulting in a MAPE of 1.7 %. For a simulation to be considered a good approximation, the MAPE should not exceed 2 % ⁽²¹⁾, ⁽²²⁾.

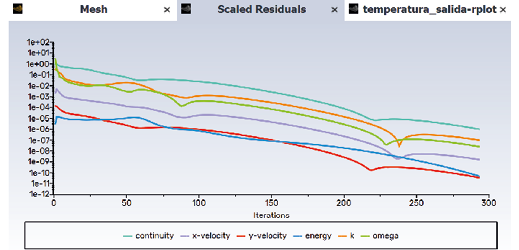
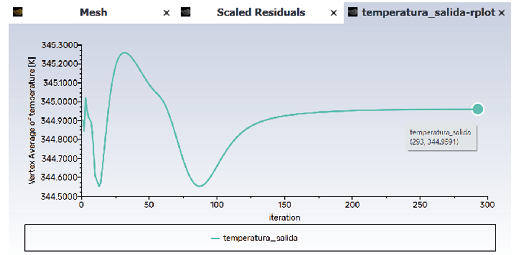
In Figure 9, the residuals are presented, which are essential for evaluating the convergence of numerical simulations. The residuals represent the difference between the calculated values and the expected values of the flow variables. For this specific case, an absolute convergence criterion of 1e-06 is used, ensuring adequate accuracy in the simulation results.

InFigure 10, the average temperature curve at the pipeline outlet can be observed. The temperature at which the simulation converges is 344.95 K, which is reached at iteration 293.

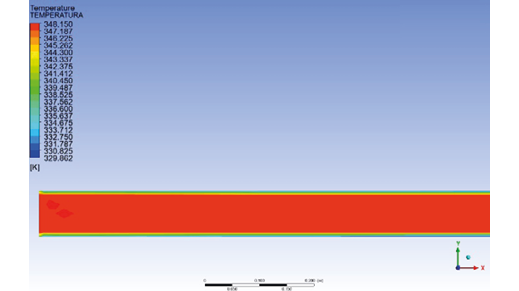
InFigure 11, the temperature profile at the pipeline inlet can be observed, representing the highest temperature recorded in this simulation. Specifically, the crude oil temperature at the inlet of the analyzed section is 348.15 K. It can be seen that the closer the heavy crude is to the surface of the pipeline, the lower the temperature.

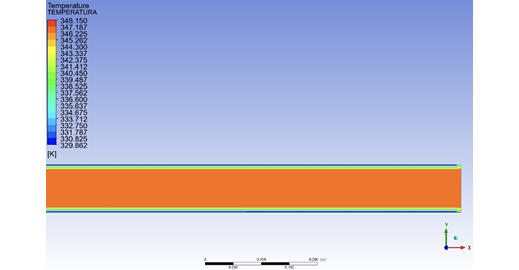
InFigure 12, the temperature profile at the pipeline outlet can be observed. This area has the lowest temperature recorded in this simulation. Specifically, the crude oil temperature at the outlet of the analyzed section is 344.95 K. Similar to the start of the analyzed section, it can be seen that the closer the heavy crude is to the surface of the pipeline, the lower the temperature.

IV. DISCUSSION

From the experimental and simulation results, it can be observed that there is a temperature reduction from 348.15 K at the starting point of the analysis to 344.95 K at the endpoint of the 50 m pipeline section. This temperature decrease is due to the ambient air temperature being 292.15 K. The primary reason for the heat loss is convection with the environment. The convective coefficient determined through the simulation is 52 W/m²·K. This coefficient can be used to evaluate the temperature loss over long pipeline sections, allowing for the determination of the heat that needs to be added to the fluid. Temperature loss in the pipeline during transport significantly affects the viscosity of heavy crude, which in turn influences the efficiency and costs associated with pumping it over long distances.

The simulation identifies that the variables most influencing this heat loss are the ambient temperature, the crude temperature, the convective heat transfer coefficient, and the crude velocity. Other parameters that also influence but cannot be modified include the area exposed to the environment, and the thermal properties of the pipeline and the fluid. Ambient temperature affects heat loss because, according to Newton’s law of cooling, the rate of heat loss from the pipeline is proportional to the temperature difference between the pipeline and the environment. Crude temperature is important in heat loss because a higher temperature implies a greater potential for heat loss to a cooler environment. The convective heat transfer coefficient is crucial in heat loss, as the loss occurs primarily through convection. The convective transfer coefficient is directly proportional to the heat loss. The crude flow velocity is critical since a higher velocity implies that the crude remains in contact with the environment for less time, resulting in lower heat losses. Conversely, a lower velocity means that the crude is exposed to the environment for a longer time, increasing the heat losses.

V. CONCLUSION AND RECOMMENDATIONS

Through the application of computational fluid dynamics, it was possible to quantify the temperature variation along a 50-meter segment of heavy crude oil transportation pipeline, determining that there is a 3.2 K reduction in the analyzed section. Additionally, the convective coefficient was found to be 52 W/m²·K. This analysis provided a detailed understanding of the temperature profiles and thermal dynamics involved, which is essential for optimizing transportation processes and ensuring the operational integrity of the system. The results obtained offer valuable insights for the design and improvement of thermal maintenance strategies, significantly contributing to the efficiency and safety in the management of heavy crude transportation.

The results obtained serve as a foundation for future studies that introduce heating technologies for heavy crude to maintain its viscosity within optimal ranges for efficient transportation.