1. Introducción
Comúnmente el agua y la energía están interrelacionadas dentro de un proceso. Si bien el uso mínimo de agua puede conllevar al ahorro de materias primas y del combustible utilizado para los procesos de calentamiento o enfriamiento, el suceso inverso también se manifiesta. Por consiguiente, los consumos de agua y energía deberían racionalizarse de forma simultánea. En este contexto, implementar alternativas para optimizar el uso de ambos recursos, cumpliendo con las regulaciones ambientales, constituye un reto global para ingenieros e investigadores (Ahmetović, Ibrić, Kravanja y Grossmann, 2015; Lorenzo-Llanes, Zumalacárregui-de Cárdenas y Mayo-Abad, 2016). A pesar de que esta premisa parece incuestionable en la actualidad, siempre existen posibilidades de mejora en el ámbito industrial.
El sistema estudiado en el presente trabajo constituye un elemento clave en la gestión energética de la planta de procesos químicos donde se encuentra instalado. El mismo está compuesto por dos intercambiadores de calor de tubos y coraza enchaquetados, cuya función es enfriar el sulfuro de hidrógeno desde 416.15 hasta 310.15 K y separar el azufre arrastrado por la corriente de gas. Son equipos que operan con tres fluidos y poseen dos vías principales de intercambio de calor, ya que el aislamiento térmico externo limita la transferencia con el entorno. A pesar de que el sistema de enfriamiento se diseñó para transferir una energía térmica equivalente a 138 kW, a través de un área efectiva de 49.2 m., actualmente no se alcanza el intercambio térmico proyectado. De una parte, el flujo de agua alimentado representa solamente entre un 53.5 y 56.6 % del valor de diseño, equivalente a 2.974 kg/s (Sánchez-Escalona, Góngora-Leyva, Zalazar-Oliva y Álvarez-Hernández, 2017). Por otra parte, la distribución de los flujos de agua no es óptima porque limita la eficiencia del proceso de transferencia de calor. Como la carga térmica de cada etapa de intercambio es diferente, y en la mayoría de los escenarios de operación analizados el agua no es la resistencia térmica controlante, no tiene sentido práctico distribuir los flujos equitativamente en cada intercambiador de calor. Ello provoca que los equipos se subutilicen desde el punto de vista energético y se desaproveche potencia de bombeo en el sistema de suministro de agua.
Aunque varios investigadores han analizado la disposición óptima de las corrientes para intercambiadores de calor aislados (Gaddis, 1986; Kumar-Singh, 2015) y para corazas múltiples en serie (Mukherjee, 2004; Kotiaho, Lampinen y Assad, 2015; Guo, Cui, Huai, Cheng y Zhang, 2019), con el fin de mejorar la efectividad térmica del sistema, la mayor parte de la literatura solo hace referencia a configuraciones en paralelo y contracorriente de los fluidos. El arreglo combinado, serie-paralelo, ha sido poco estudiado. Mukherjee (2004) analizó este escenario mediante una situación real presentada en una refinería, con un sistema de enfriadores de hidrocarburo líquido, y propuso dividir el flujo de agua entre las corazas de la primera y la segunda etapa, en la misma proporción de sus cargas térmicas. La complejidad de este caso no fue notable, porque los equipos analizados solo poseían dos fluidos y una vía principal de intercambio de calor. Un estudio posterior fue realizado por Sánchez-Escalona y Góngora-Leyva (2019), relacionado también con la disposición serie-paralelo pero considerando tres fluidos, en el cual se estableció un procedimiento para el análisis térmico de los intercambiadores de calor, que permitió proponer mejoras a las instalaciones industriales existentes. Aunque recomendaron incrementar el flujo de agua a cada intercambiador de calor hasta 7.5 kg/s, con el propósito de lograr la temperatura requerida de salida del gas, la optimización de los flujos hacia cada sección del sistema se reservó para estudios posteriores.
Otro grupo de investigadores han empleado métodos de optimización y técnicas de intensificación de la transferencia de calor para incrementar el rendimiento térmico de los equipos (Sheikholeslami, Gorji-Bandpy y Ganji, 2015; Reyes-Rodríguez y Moya-Rodríguez, 2016; Toimil y Gómez, 2017; Alam y Kim, 2018). En este ámbito, cuando se estudian las mejoras de redes preexistentes de intercambiadores de calor (HEN retrofit), se tienen en cuenta dos escenarios principales: estructura fija de la red, y modificación de la topología. Mediante la primera se persigue maximizar la recuperación de calor en la red utilizando superficies extendidas, insertos de cinta en espiral, deflectores helicoidales u otras técnicas. En cambio, mediante la segunda, se tienen en consideración todas las posibilidades de modificación de la red, incluyendo cambios del área de transferencia y nueva disposición de los sistemas de tuberías. Aunque la modificación de la topología permite mejor aprovechamiento del agua y la energía, también implica mayores costos capitales (Jiang et al., 2018). Además, en plantas de producción continua, por lo general se dificulta realizar este tipo de modificaciones, incitando preferencia por la primera opción.
La mejora de redes preexistentes de intercambiadores de calor ha sido ampliamente estudiada. Dentro de los trabajos más recientes se encuentran los de desarrollados por Jiang et al. (2018), Bütün, Kantor, Mian y Maréchal (2018), Biyanto et al. (2019), Klemeš et al. (2020), entre otros. Sin embargo, en las referencias consultadas no se han analizado intercambiadores de calor con tres fluidos, ni se consideró la optimización de los flujos de las corrientes secundarias como uno de los métodos de intensificación de la transferencia de calor sin modificar la topología existente. Teniendo en cuenta lo anterior, el objetivo de este trabajo consiste en proponer un esquema optimizado de distribución de agua a los intercambiadores de calor, que posibilite un aumento de la termotransferencia en el sistema de enfriadores de sulfuro de hidrógeno, manteniendo una estructura fija de la red. El enfoque presentado logra una solución factible y sencilla de un problema industrial.
2. Materiales y métodos
2.1. Metodología de optimización
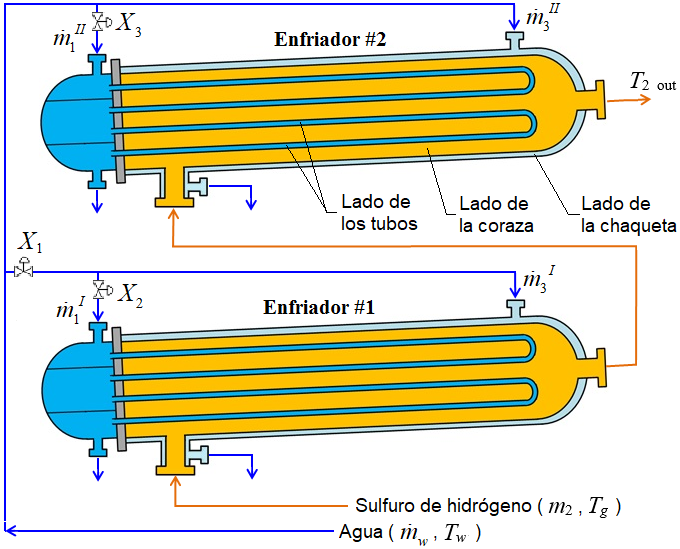
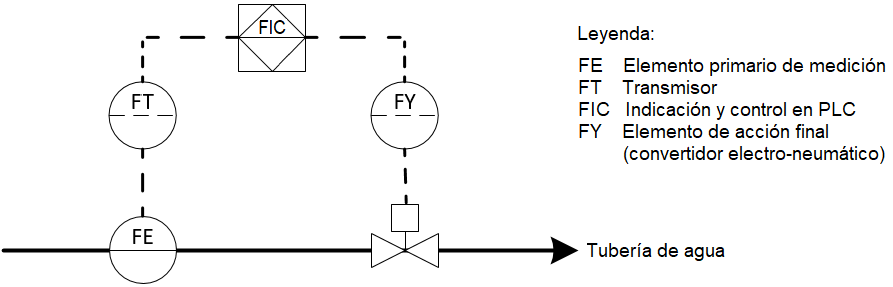
El sistema de enfriamiento estudiado está compuesto por dos intercambiadores de calor de tubos y coraza enchaquetados, instalados en un arreglo serie-paralelo (flujo de gas en serie, y los de agua en paralelo). En cada uno de ellos el sulfuro de hidrógeno hace su recorrido del lado de la coraza en un paso, mientras que el agua circula del lado de los tubos, con cuatro pasos, y también por la chaqueta exterior (figura 1). Sus dos vías principales de intercambio de calor son: coraza-tubos y coraza-chaqueta. Los equipos operan ocho horas en modo de enfriamiento del gas, y luego se sacan de operación para suministrarle vapor (por el lado de los tubos y por la chaqueta), durante cuatro o seis horas con el objetivo de eliminar el azufre incrustado en su interior.
La optimización de los flujos de agua en este sistema se realizó mediante algoritmos genéticos, utilizando un modelo basado en el método de la Efectividad - Número de Unidades de Transferencia (ɛ-NUT), para la simulación de los intercambiadores de calor. La metodología empleada constó de los siguientes pasos:
1. Diagnóstico termoenergético del objeto de estudio.
2. Selección de las variables y diseño experimental.
3. Modelación del sistema de intercambiadores de calor.
4. Validación del modelo.
5. Cálculo de las temperaturas de salida y la cantidad de calor transferida para el caso base (la operación actual).
6. Optimización de los flujos de agua mediante algoritmos genéticos.
7. Cálculo de las temperaturas de salida y la cantidad de calor transferida para el caso mejorado.
8. Comparación de los resultados.
9. Determinación de las funciones para solución tecnológica del problema investigado.
2.2. Selección de las variables y diseño experimental
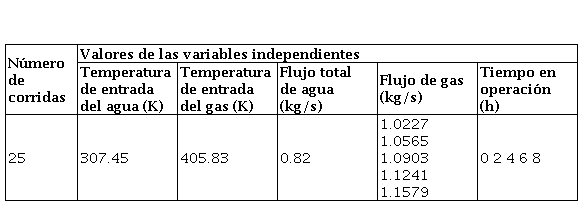
Como variables del estudio se emplearon los parámetros operacionales que tienen un efecto notable en el proceso de intercambio térmico analizado. Por lo tanto, las variables independientes seleccionadas fueron las temperaturas de entrada de los fluidos, los flujos másicos y el tiempo en operación, mientras que las variables dependientes consistieron en las temperaturas de salida de las tres corrientes. El tiempo en operación se incluyó como variable independiente, en este caso particular, debido a su influencia significativa en el factor de incrustaciones y, consecuentemente, su efecto negativo en el coeficiente global de transferencia de calor (Sánchez-Escalona y Góngora-Leyva, 2018). Los niveles de cada variable se obtuvieron a partir de los parámetros de trabajo del objeto de estudio.
Los cálculos se efectuaron destacando dos variables predictoras: flujo másico de sulfuro de hidrógeno y tiempo en operación transcurrido. El resto de los parámetros se consideraron constantes, debido a su comportamiento estable durante el proceso productivo. El número de corridas se obtuvo mediante un diseño multifactorial 5., de acuerdo con los niveles determinados para cada una de las variables, como muestra la tabla 1 (Edmonds y Kennedy, 2017).
2.3. Modelación matemática de los intercambiadores de calor
Uno de los aspectos más importantes para garantizar el éxito del proceso de optimización es la correcta formulación del modelo, ya que debe reflejar el problema real, con precisión suficiente para que los resultados tengan significación práctica (Biegler, 2014). En este contexto, para el cálculo de las temperaturas de salida de los tres fluidos que intervienen en el proceso de termotransferencia, se empleó el modelo analítico propuesto por Sánchez-Escalona y Góngora-Leyva (2018), incorporando algunas mejoras. Este modelo, representado de forma simplificada, mediante la expresión 1, se sustenta en la ecuación de la cantidad de calor transferida (según la Primera Ley de la Termodinámica), la ecuación de balance energético, así como las expresiones propias del método ɛ-NUT, particularizadas a intercambiadores de calor con tres fluidos y dos vías principales de intercambio térmico. Para ello se asumieron flujos monofásicos, propiedades termo-físicas constantes, a través del intercambiador de calor, operación en condiciones de estado estacionario y transferencia de calor nula hacia el medio ambiente.
Donde: .1 out - temperatura de salida del agua del lado de los tubos (K); .2 out - temperatura de salida del gas que fluye por la coraza (K); .3 out - temperatura de salida del agua del lado de la chaqueta (K); . - cantidad de calor total transferido en el intercambiador (W); .. - temperatura de entrada del gas (K); .. - temperatura de entrada del agua (K);
.. - flujo másico de agua del lado de los tubos (kg/s); .. - flujo másico de gas (kg/s); .. - flujo másico de agua del lado de la chaqueta (kg/s); . - tiempo en operación (h). Para este caso de estudio .2 in = T. y .1 in = .3 in = T..
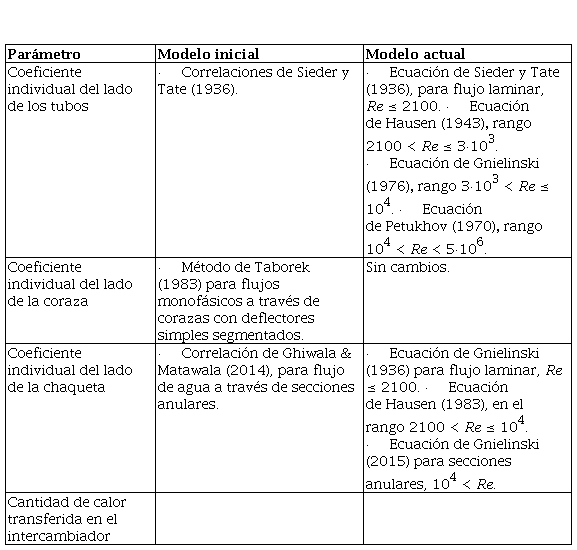
Las mejoras del modelo se introdujeron en los módulos de cálculo de los coeficientes individuales de transferencia de calor, y en la ecuación para determinar la cantidad de calor transferida (tabla 2).
Donde: Re- número de Reynolds; .. - cantidad de calor absorbida por el agua del lado de los tubos (W); .. - cantidad de calor cedida por el gas (W); .. - cantidad de calor absorbida por el agua del lado de la chaqueta (W).
2.4. Validación del modelo
Para validar el modelo se ejecutaron tres observaciones experimentales en días alternos, durante ocho horas, a partir de la puesta en funcionamiento de los intercambiadores de calor en modo de enfriamiento. Durante cada ciclo se ejecutaron 20 mediciones del flujo másico y las temperaturas de entrada y de salida de cada fluido, en ambos intercambiadores de calor, obteniéndose una base de datos con 120 registros. Instrumentación utilizada:
· Temperaturas: termopozos y termómetros bimetálicos industriales Ashcroft, con precisión de 0,1 K.
· Flujo de agua: caudalímetro ultrasónico Proline Prosonic Flow 93T, con precisión de 6.3·10-6 m./s.
· Flujo de sulfuro de hidrógeno: señal de proceso 4-20 mA que se envía a un PLC Siemens S7-400 y sistema Citect SCADA 7.10, con precisión 10-4 kg/s.
Los resultados predichos por el modelo se compararon con los valores de temperatura de salida medidos experimentalmente. Los parámetros estadísticos utilizados para cuantificar la precisión fueron el coeficiente de determinación (..), el error relativo promedio (eave ) y el error relativo máximo (emax ), calculados mediante las ecuaciones 2-4 (Tamayo-Ávila et al., 2015; Li y Lu, 2018; Tuyen, Hap, y Phu, 2020).
Donde: . - valor de temperatura medido experimentalmente (K); T’ - valor de temperatura predicho por el modelo (K); . - valor i-ésimo de la muestra; . - cantidad total de observaciones efectuadas.
2.5. Algoritmo de optimización
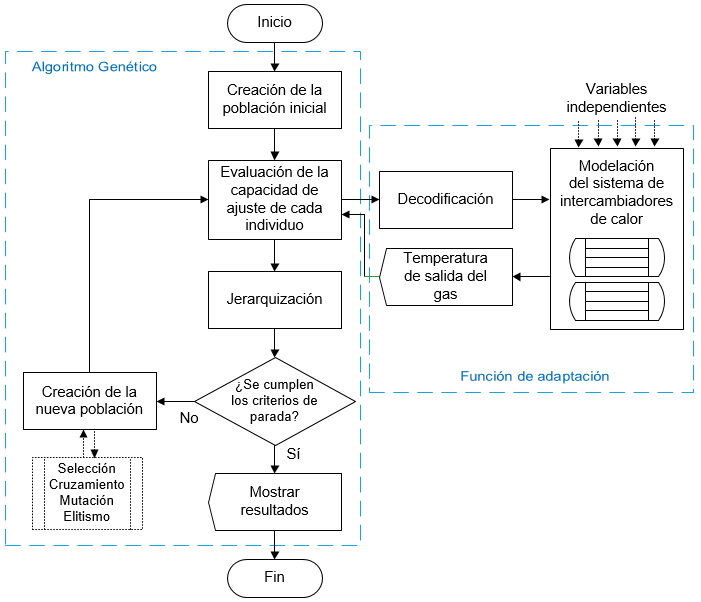
Los elementos indispensables en la formulación de problemas de optimización incluyen el modelo matemático del sistema, una función objetivo (o función de adaptación), que cuantifique el criterio que será minimizado o maximizado; variables que se puedan emplear para la toma de decisiones y, opcionalmente, las restricciones (Biegler, 2014). En tal sentido, el presente trabajo empleó la lógica que muestra el esquema de la figura 2.
El proceso de optimización se realizó mediante algoritmos genéticos, por las ventajas que ofrece esta técnica estocástica de búsqueda iterativa, inspirada en los principios de selección natural. La solución del problema se realiza imitando los mecanismos de evolución de las especies, aplicando operadores genéticos básicos: selección, cruzamiento y mutación. Como concepto, un conjunto de individuos (población) cambia de generación en generación, sufriendo un proceso de evolución y adaptándose cada vez mejor al entorno. Su analogía matemática consiste en disponer de una función a maximizar o minimizar y una zona de búsqueda del elemento deseado, de manera que a cada punto del espacio de búsqueda le corresponde un valor de la función objetivo, y la meta es encontrar el punto que optimice dicha función (Reyes-Rodríguez y Moya-Rodríguez, 2016; Najarro, López, Racines y Puris, 2017; Moslemi y Keshtkar, 2018).
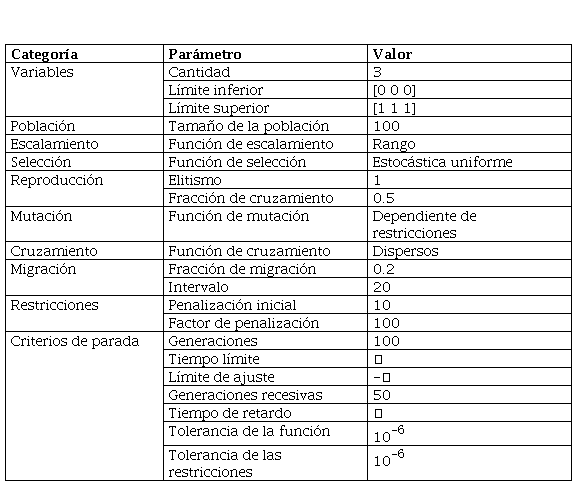
En la investigación se utilizaron funciones desarrolladas en Matlab® para efectuar la optimización. Los parámetros relacionados con la configuración del algoritmo se detallan a continuación (tabla 3).
En el presente estudio la función de adaptación a minimizar consistió en la temperatura del gas a la salida del enfriador 2 (.. II out ). Para su cálculo se utilizó el modelo descrito en el acápite 2.3. El módulo de decodificación, que utiliza las variables del algoritmo genético (.., .. y ..), para establecer los flujos de agua a cada sección del sistema de intercambiadores de calor, se basó en las ecuaciones 5-8.
Distribución de los flujos de agua en el enfriador 1 (etapa I):
Distribución de los flujos de agua en el enfriador 2 (etapa II):
Donde: m. - flujo total de agua alimentado al sistema de intercambiadores de calor, equivalente a 0.82 kg/s. Los superíndices I y II representan la primera y la segunda etapa de enfriamiento, respectivamente.
Desde el punto de vista práctico, el parámetro .. denota la fracción del flujo total de agua que se bombea hacia el primer enfriador, siendo 1 – .. la fracción remanente hacia el segundo equipo. Por otra parte, .. representa la fracción del flujo de agua en el primer intercambiador que se hace fluir a través de los tubos, mientras que 1 – .. constituye la porción que circula por la primera chaqueta. De forma análoga, .. describe la fracción que fluye por los tubos del segundo enfriador, y 1 – .. la que circula por la segunda chaqueta. Para el caso base (la operación actual del sistema de enfriamiento), se comprobó experimentalmente que .. = 0,500 y .. = .. = 0,723, con tendencia invariable.
2.6. Funciones para solución tecnológica del problema investigado
Para correlacionar los flujos de agua óptimos hacia cada sección de los intercambiadores de calor, en función del flujo másico de sulfuro de hidrógeno y del tiempo en operación, se aplicó un análisis de regresión lineal múltiple. El cálculo de los coeficientes en este modelo tuvo como base el método de mínimos cuadrados, debido a su conveniencia matemática y a la posibilidad de obtener expresiones explícitas de las ecuaciones de regresión (Bhattacharya y Burman, 2016). El análisis de la varianza, determinación de la bondad de ajuste y verificación de las hipótesis del modelo, se realizaron con el programa computacional Statgraphics.
3. Resultados y discusión
3.1. Modelación matemática
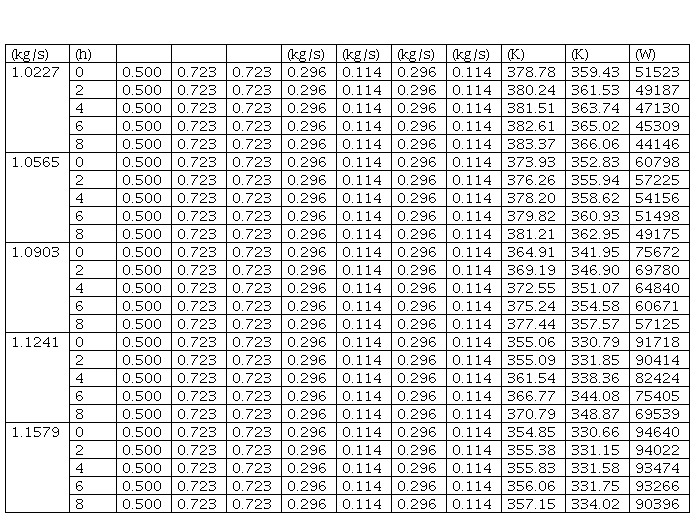
El sistema de enfriamiento de sulfuro de hidrógeno se estudió a partir de la matriz experimental diseñada. Los principales resultados obtenidos para el caso base se muestran a continuación (tabla 4).
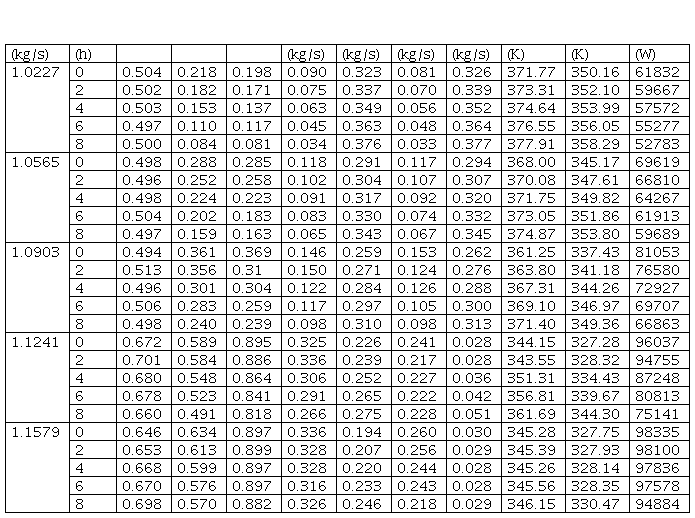
Por otra parte, al optimizar los flujos de agua hacia cada sección del sistema de intercambiadores de calor, mediante algoritmos genéticos, se obtuvieron los valores de temperaturas de salida y cantidad de calor transferida para el caso mejorado (tabla 5).
Donde: ...out - temperatura del gas a la salida del primer enfriador (K); .. II out - temperatura del gas a la salida del segundo enfriador (K); Q. - cantidad de calor total transferida en el sistema, incluyendo ambas etapas (W).
La precisión del modelo analítico utilizado para simular el desempeño térmico de los intercambiadores de calor, garantizó confiabilidad de los resultados. Al comparar las predicciones con los valores de temperatura de salida medidos experimentalmente se observó fuerte grado de asociación entre las variables y bajos índices de error (figura 3).
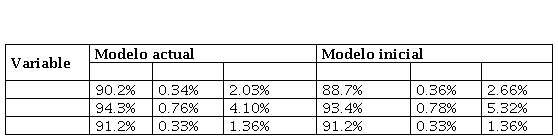
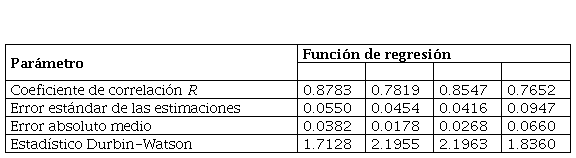
Las mejoras al modelo inicial publicado por Sánchez-Escalona & Góngora-Leyva (2018), introducidas en este estudio, posibilitaron incrementar la correlación y reducir ligeramente las desviaciones (tabla 6).
3.2. Comparación del caso mejorado con el caso base
Operar con flujos de agua estables y balanceados hacia las diferentes secciones del sistema de intercambiadores de calor, impide alcanzar mayores niveles de eficiencia térmica. Como los dos intercambiadores poseen el mismo tamaño y capacidad, la coraza más caliente entrega mayor carga térmica que la otra, en virtud de una mayor diferencia media de temperaturas (Mukherjee, 2004; Sánchez-Escalona y Góngora-Leyva, 2017). Esto provoca que el agua de enfriamiento, bombeada al intercambiador de calor de la primera etapa, absorba más calor y de cierta manera se subutilice la capacitancia térmica de la corriente de agua a través de la segunda etapa. Además, como el agua no es el fluido controlante, cualquier exceso de flujo solo tendrá una influencia imperceptible en los coeficientes globales de transferencia de calor.
Teniendo esto en consideración, los valores óptimos de termotransferencia se estimaron para flujos de agua variables, que deben ajustarse en función del nivel productivo de sulfuro de hidrógeno y del tiempo en operación transcurrido. El hecho de que la transferencia óptima de energía térmica dependa de flujos de agua variables, también obedece al uso de intercambiadores de calor con más de una vía de intercambio térmico, ya que la efectividad máxima solo se alcanza cuando la sumatoria de todas las cantidades de calor transferido sea superior. Bajo estas circunstancias, las corrientes de agua pueden dividirse coordinadamente hacia las diferentes secciones de los intercambiadores de calor, abasteciendo con mayor flujo a la vía de intercambio de calor, que ofrece menor resistencia térmica. En este caso de estudio, las resistencias térmicas controlantes son el coeficiente individual de transferencia de calor del lado de la coraza y el factor de incrustaciones, por lo que estas definen la matriz de distribución de los flujos de agua.
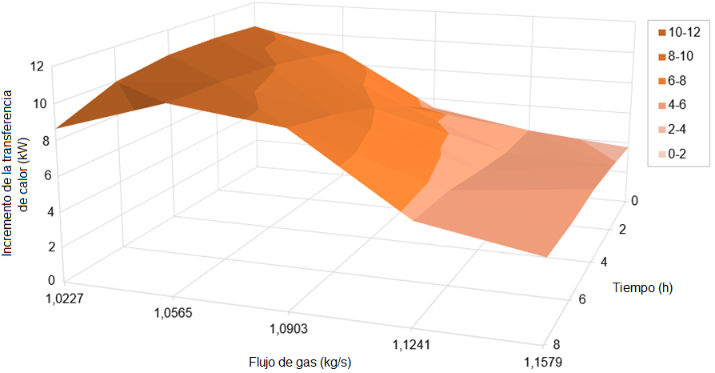
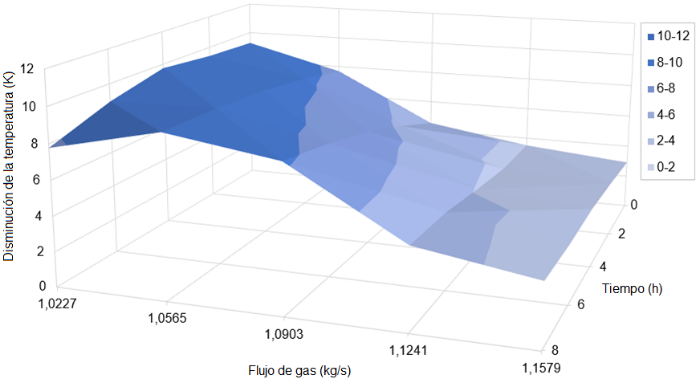
El esquema de optimización propuesto permite incrementar la cantidad de calor transferida entre 3695 y 10514 W (figura 4). Consecuentemente, se logra disminuir la temperatura del gas a la salida del sistema de enfriamiento entre 2.9 y 9.8 K (figura 5). Este hecho no solo favorece un uso racional del agua, sino también un mejor aprovechamiento de la potencia de bombeo y, por consiguiente, un uso más eficiente de la energía eléctrica generada. El impacto primario de esta mejora, en materia de utilización de recursos, consiste en lograr que se transfiera una mayor cantidad de energía térmica sin la necesidad de incrementar el flujo total de agua de enfriamiento, que es bombeado a través del sistema de intercambiadores de calor.
Según Jiang et al. (2018), cuando se aplican técnicas de mejora de las redes de intercambiadores de calor (HEN retrofit), imponiendo estructura fija de la red (uso de superficies extendidas, insertos de cinta en espiral, deflectores helicoidales, etc.), la recuperación termoenergética puede elevarse hasta un 7.69 %. En el presente caso de estudio se determinaron niveles de recuperación comparables, que oscilan entre 3.90 y 22.16 %, con 12.44 %, como promedio.
3.3. Propuesta de funciones para la implementación práctica
Los flujos de agua óptimos, hacia cada sección de los intercambiadores de calor, se correlacionaron con el flujo másico de sulfuro de hidrógeno y el tiempo en operación, como muestran las ecuaciones 9-12:
Al ajustar los modelos de regresión lineal múltiple se caracterizó la significancia estadística de cada función, determinándose una correlación moderada-fuerte (tabla 7). Como el valor-P resultante de los análisis de varianza fue menor que 0.05 en todos los casos, existe una relación estadísticamente significativa entre las variables con un nivel de confianza del 95 %.
A partir de estos resultados se propone instalar una válvula automática con lazo de control de flujo (figura 6), en cada ramal de las tuberías de agua, hacia los intercambiadores de calor, incorporando las funciones obtenidas en un autómata programable (PLC) Siemens S7-400 disponible en la planta.
Este sistema permite mejorar el intercambio térmico manteniendo constante el flujo total de agua, porque se fundamenta en una distribución inteligente y dinámica de los caudales hacia las diferentes secciones de los intercambiadores de calor, sin tener que modificar el sistema de bombeo existente. En investigaciones precedentes sobre el mismo objeto de estudio (Sánchez-Escalona y Góngora-Leyva, 2019) se recomendó incrementar el flujo de agua a cada equipo, sin optimizar su distribución, pero ello implicaría continuar operando de modo menos eficiente, y demandaría la sustitución de todo el sistema de bombeo y suministro de agua por otro de mayor caudal, con costos más elevados.
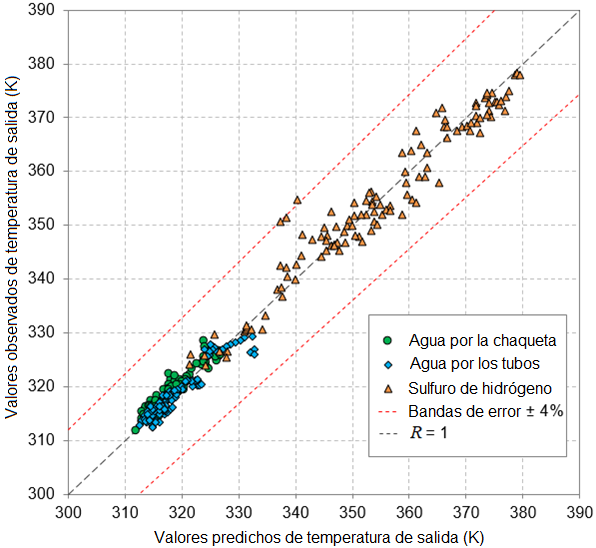
Figura 3 Validación del modelo. Las mejoras al modelo inicial publicado por Sánchez-Escalona & Góngora-Leyva (2018), introducidas en este estudio, posibilitaron incrementar la correlación y reducir ligeramente las desviaciones(tabla 6).
4. Conclusiones
Se propuso un esquema optimizado de distribución de agua a los intercambiadores de calor (manteniendo constante el flujo total alimentado al sistema, m. = 0.82 kg/s), que mejora la eficiencia térmica del sistema de enfriamiento de sulfuro de hidrógeno sin realizar modificaciones constructivas importantes en la red. La solución del problema de optimización se desarrolló satisfactoriamente, empleando algoritmos genéticos. El modelo utilizado para la simulación de los intercambiadores de calor se considera confiable, a partir de los valores de los parámetros estadísticos calculados: coeficiente de determinación ascendente a 94.3 %, y error relativo máximo equivalente a 4.1 %.
Los valores óptimos de termotransferencia se estimaron para flujos de agua variables, determinados en función del flujo másico de sulfuro de hidrógeno y del tiempo en operación. Se estimó un incremento del calor transferido entre 3695 y 10514 W, así como una disminución de la temperatura del gas a la salida del sistema entre 2.9 y 9.8 K. La recuperación termoenergética calculada osciló entre 3.90 y 22.16%, con 12.44 % como promedio. El trabajo aporta una solución tecnológica del problema investigado, que consiste en la instalación de válvulas automáticas con lazos de control de flujo gobernados desde un PLC.
Las oportunidades futuras de investigación deberían enfocarse en el empleo de otras técnicas de regresión, para mejorar la bondad de ajuste de las funciones que correlacionan los flujos de agua óptimos con el flujo de sulfuro de hidrógeno y el tiempo en operación. También podría estimarse el impacto económico que introduce un proceso de transferencia de calor más eficiente, que a su vez implica un mejor aprovechamiento de la potencia de bombeo de agua.