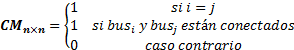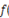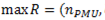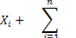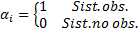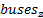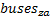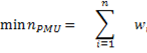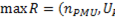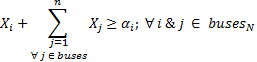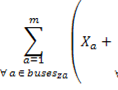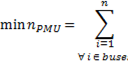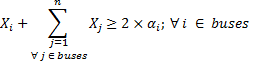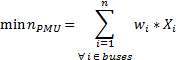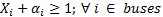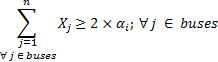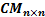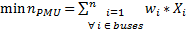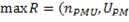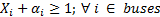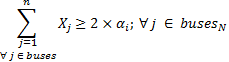Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introducción
Los sistemas eléctricos de potencia (SEP) no solo están conformados por elementos eléctricos, como generadores, cables, transformadores, entre otros; sino que se apoyan en las nuevas tecnologías para que su operación cumpla los parámetros de calidad, confiabilidad y seguridad exigidas por los usuarios (Carrión, González, Isaac, López, y Cardona, 2017; Guerrón, García, y Montero, 2014; Maldonado, 2017; Ruíz, Masache, y Domínguez, 2018). De allí es que nace el concepto de red inteligente, donde los sistemas eléctricos apoyados de las comunicaciones se convierten en sistemas más eficientes; en los cuales se tiene un mejor control de los diferentes parámetros eléctricos (Carrión, García, et al., 2017; García, López, y Millán, 2018; García y Millán, 2018).
La medición de los parámetros eléctricos en los SEP se la realiza mediante unidades de medición fasorial (PMU) en su etapa de transmisión, y medidores inteligentes (SM) en la etapa de distribución (Cevallos, Intriago, Plaza, e Idrovo, 2018; Sánchez y Carrión, 2017). Las PMU, poseen un reloj de tiempo real (RTC) y un sistema de posicionamiento global (GPS); cuya función es medir los fasores de tensión y corriente del SEP y enviarlos al centro de control en donde se analiza el comportamiento del SEP en tiempo real (Arciniegas, Imbajoa, y Revelo, 2017; Jiang, Li, Wang, y Wang, 2012; Jiang, Miao, Xu, Liu, y Zhang, 2012; Mccamish et al., 2017; Song, Ma, Wu, Quan, y He, 2009).
La ubicación de las PMU a lo largo de los SEP es un tema de estudio que busca minimizar la cantidad de unidades desplegadas en el sistema de potencia, con la característica que la observabilidad del SEP se mantenga. Para el despliegue óptimo de PMU se utilizan técnicas numéricas de optimización, técnicas heurísticas y técnicas de inteligencia artificial (Huang et al., 2014; Mori y Tsuzuki, 1991).
Las técnicas de optimización numéricas más utilizadas son: programación lineal entera mixta (MIP) y programación no lineal entera mixta (MINP) (Carrión, González, Isaac, y López, 2017; Gou, 2008; Bei Gou, 2008); las técnicas heurísticas de mayor uso son: búsqueda tabú (TS), recocido simulado (SA), optimización de enjambre de partículas (PSO), optimización mediante colonia de hormigas (ACO) y búsqueda armónica (HS) (Kekatos, Giannakis, y Wollenberg, 2012; Korres, Georgilakis, Koutsoukis, y Manousakis, 2013; Manousakis, Korres, y Georgilakis, 2011; Nuqui y Phadke, 2005; Taher, Mahmoodi, y Aghaamouei, 2016) y las técnicas de inteligencia artificial para la ubicación de PMU más frecuentes son: algoritmos genéticos (GA), redes neuronales (NN) y control difuso (FL). Por otro lado, están las técnicas basadas en la teoría de grafos (GT) como son las técnicas de clusterización mediante k-means y k-medioids (Carrión, Inga, González, e Hincapié, 2016; Grigoras, Cartina, y Gavrilas, 2009; Inga, Carrión, Águila, García, y Hincapié, 2016; Ketabi, Nosratabadi, y Sheibani, 2012; Srivastava, 2015; Werho, Member, Vittal, Kolluri, y Wong, 2016; Zhu, Duan, Zhang, Qi, y Huang, 2013).
El problema de minimizar la cantidad de PMU desplegadas en los SEP es un problema de optimización NP-Completo con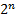 
posibles soluciones en un SEP de n-buses, lo cual representa un problema combinacional. Al reducir las PMU se logra minimizar la cantidad de datos que son transmitidos al centro de control, reduciendo las necesidades informáticas para almacenar la base de datos (Correa, Inga, Inga, e Hincapié, 2018; Inga Ortega, Inga, Correa, e Hincapié, 2018; Moscoso-Zea y Lujan-Mora, 2017).
Los sistemas de potencia están conformados por buses PV que tienen al menos un generador conectado a dicho bus; buses PQ que representan los buses en los cuales se tiene carga; buses ZIB en los cuales no existe generación ni carga y buses SLACK que representa el bus principal del SEP; en (Akhlaghi, 2016) se analiza la ubicación óptima de PMU considerando buses ZIB, mejorando las propuestas en las cuales no se realizaba dicha consideración.
La ocurrencia de contingencias en los SEP es una situación que se debe considerar al analizar el comportamiento del sistema eléctrico, en (Aminifar, Khodaei, Fotuhi-Firuzabad, y Shahidehpour, 2010; Esmaili, Shayanfar, y Gharani, 2014; Paudel, Xu, Balasubramaniam, y Makram, 2015; Rahman y Zobaa, 2016; Sodhi, Srivastava, y Singh, 2009) se considera la ubicación óptima de PMU y otros dispositivos de medición en caso de contingencia en el SEP, considerando como contingencia la salida de operación de una línea de transmisión y en (Akhlaghi, 2016) se considera la salida de operación de una PMU.
El objetivo de la presente investigación, que es una extensión de Carrión y González (2018), es minimizar la cantidad de PMU desplegadas en el SEP, respetando restricciones de observabilidad, redundancia, buses ZIB y contingencias N-1. Como supuestos de la investigación se considera como contingencia la salida de operación de cualquier elemento del SEP, incluso la falencia de una PMU; también se supone que la red de comunicaciones está desplegada y funciona correctamente. Para verificar el modelo propuesto se utilizaron los sistemas de prueba del IEEE de 9, 14, 30 y 118 barras, verificando la utilidad del algoritmo al comparar la cantidad de PMU con y sin restricción de contingencia N-1.
En adelante, el artículo se organiza de la siguiente manera: en la sección 2 se introducen los fundamentos de la ubicación óptima de PMU; en la sección 3 se describe la formulación del problema, en la sección 4 se analiza el desempeño de la metodología propuesta bajo diversas condiciones; finalmente, las conclusiones del trabajo se presentan en la sección 5.
2. Ubicación óptima de Unidades de medición fasorial
Para el despliegue óptimo de PMU en los sistemas de potencia se debe identificar la matriz de conectividad (CM), la cual es diferente para cada SEP. CM es una matriz cuadrada de dimensión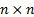 
, cuyos valores 
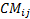son 1 o 0; 
es la cantidad de buses del sistema. CM representa la topología del SEP y se la puede determinar mediante la Ecuación 1.
(1)
Donde:
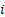; representa el nodo de salida
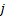; representa el nodo de llegada
La observabilidad del SEP se fundamentes en tres reglas, con las cuales se puede tener la medición directa o indirecta de los fasores de tensión y corriente (Carrión y González, 2018).
Regla 1: Si se conocen el voltaje y la corriente en un lado de cualquier ramal, aplicando la Ley de Ohm se puede determinar sus valores en el otro lado del ramal.
Regla 2: Las ZIB y sus incidencias, si solo un bus es inobservable mediante la ley de Kirchhoff de corriente el bus se lo puede hacer observable.
Regla 3: Si se conoce el fasor de voltaje en ambos lados del ramal, los fasores de corriente se los puede obtener.
2.1 Despliegue óptimo de PMU con restricciones de observabilidad y redundancia
En la Ecuación 2 se tiene la función objetivo para minimizar la cantidad de PMU a ser colocadas; si solo se consideran las restricciones de observabilidad y redundancia. En las Ecuaciones 3, 4 y 5, se encuentran las restricciones del problema de optimización respetando la observabilidad del sistema del 100 % y redundancia de mediciones (Jaramillo y Carrión, 2016).
F.O.:
(2)
Sujeto a:
(3)
(4)
(5)
Donde:
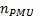; representa el número de PMUs
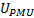; representa el nodo de ubicación
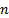; representa el número de nodos del sistema
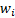; es el peso de acuerdo al costo de implementación por PMU en el bus i
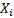; representa una variable binaria de ubicación de PMU
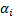; representa una variable binaria de observabilidad
2.2 Despliegue óptimo de PMU considerando buses ZIB
Al considerar adicional el efecto de los buses ZIB en el problema de optimización anterior se debe tomar en cuenta la modificación que sufre la CM y que la observabilidad quede garantizada, los buses se dividen en dos grupos:
ZIB 
o ZIB adyacentes 
El resto de buses 
o buses normales
La minimización de PMU se la realiza aplicando (6); restringido por (7) que indica que al menos el sistema posee una PMU, (8) maximiza la redundancia del sistema y (9) y (10) limitan la observabilidad al 100 %.
F. O.:
(6)
Sujeto a:
(7)
(8)
(9)
(10)
Donde:
; representa una variable binaria de ubicación de PMU en los nodos adyacentes.
2.3 Despliegue óptimo de PMU con restricciones de contingencia
Las contingencias son eventos que se presentan en los SEP con mucha frecuencia, por ello los sistemas de medición deben tener la capacidad de mantener el registro de los parámetros eléctricos aun cuando la contingencia esté presente. Para desplegar PMU de manera óptima, considerando lo expuesto anteriormente, se deben tomar en cuenta dos condiciones de contingencia: que salga de operación una línea de transmisión (L/T) o que se pierda una PMU.
Pérdida de PMU
Al igual que en el caso anterior se busca mantener la observabilidad completa del SEP para lo cual cada bus debería ser observado por 2 PMU. Mediante (11) se logra minimizar las PMU; restringido por (12) que indica que al menos el sistema posee una PMU (13) maximiza la redundancia del sistema y (14) limitan la observabilidad al 100 %
F.O.:
(11)
Sujeto a:
(12)
(13)
(14)Pérdida de línea de transmisión
En caso de que la contingencia sea la salida de una L/T se parte del concepto que cada bus debe tener instalada una PMU o que cada bus sea monitoreado por dos PMU; lo cual exigirá de muchos recursos informáticos en el centro de control, pero se tendrá la seguridad de no perder la observabilidad del sistema.
Para minimizar la cantidad de PMU desplegados óptimamente en el SEP se aplica (15); restringido por (16) que indica que al menos el sistema posee una PMU, (17) maximiza la redundancia del sistema y (18) y (19) limitan la observabilidad al 100 %.
F. O.:
(15)
Sujeto a:
(16)
(17)
(18)
(19)
3. Formulación del problema
La estimación de estado y verificación del comportamiento de un SEP, en tiempo real, se solucionó con el despliegue de PMU, por ello en la actualidad los sistemas de potencia consideran a las PMU uno de los elementos esenciales. La presente investigación se plantea el problema mantener la observabilidad del SEP ante una contingencia mediante el despliegue óptimo de PMU. Por ello se propone desarrollar una metodología que minimice la cantidad de PMU instaladas en un SEP considerando contingencias N-1, el cual se lo puede aplicar a un SEP que ya tenga desplegadas PMU y no haya considerado dicha restricción.
En el Algoritmo 1 se muestra la metodología a seguir para minimizar la cantidad de PMU, considerando restricciones de observabilidad, redundancia, ZIB y contingencias N-1. Lo primero que se realiza es identificar la CM con la cual se tiene la topología del SEP, así como también se logra identificar las ZIB; luego de ello se considera que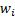 
, que representa el costo de implementación de la PMU, tiene el mismo valor para cada una de la PMU que se van a instalar y con ello se simplifica el cálculo. Posteriormente se aplica el modelo de optimización para minimizar la cantidad de PMU, considerando restricciones de observabilidad, redundancia, ZIB y contingencia N-1.
Algoritmo 1: Ubicación óptima de PMU bajo contingencia N-1
Paso 1: Input
; matriz de conectividad
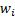; tiene el mismo valor para todas las PMU
Paso 2: Aplicar reglas de observabilidad
Paso 3: Minimización de PMU
F.O.:
Paso 4: Mostrar resultados de la optimización
Como casos de estudio se toman en consideración los modelos de prueba del IEEE de 9, 14, 30 y 118 barras; en los cuales se realizó un despliegue óptimo de PMU sin considerar la restricción de contingencia N-1, para luego aplicar el modelo con la restricción y comparar sus resultados.
4. Análisis de resultados
Para explicar los resultados obtenidos se utiliza el modelo de prueba de 30 buses del IEEE. Sobre el modelo de 30 buses en un inicio se realiza una ubicación óptima de PMU sin consideración de restricciones de ZIB ni de contingencias, lo que se puede apreciar en la Figura 1, en la cual se puede identificar que como resultado del Algoritmo se deben colocar 10 PMU, desplegadas en los buses 1, 2, 6, 10, 11, 12, 15, 19, 25 y 29.
Si ahora se consideran las restricciones de ZIB y contingencias la cantidad de PMU y su ubicación, cambian en comparación de la modelación anterior, para lo cual se aplica el Algoritmo 1. La variable 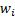sigue teniendo el mismo valor para todas la PMU, la matriz de conectividad no se ve afectada, pero se debe tener en consideración que en el bus 7; que es ZIB, no se puede instalar una PMU. Basado en todas las consideraciones anteriores ahora se tienen 16 PMU desplegadas en el SEP en los nodos 2, 3, 7, 8, 10, 11, 12, 13, 15, 16, 19, 21, 24, 26, 27 y 29; como se aprecia en la Figura 2; en comparación con la modelación anterior, la cantidad de PMU crece en 6 unidades.
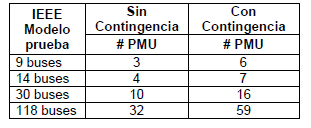
Aplicando el Algoritmo 1 para todos los modelos propuestos se logra determinar la cantidad mínima de PMU que se necesitan desplegar en cada uno de los SEP, considerando que en los mismos se puede producir contingencias. En la Tabla 1 se puede apreciar la diferencia en la cantidad de PMU que se necesitan en cada uno de ellos con y sin la restricción de contingencia.
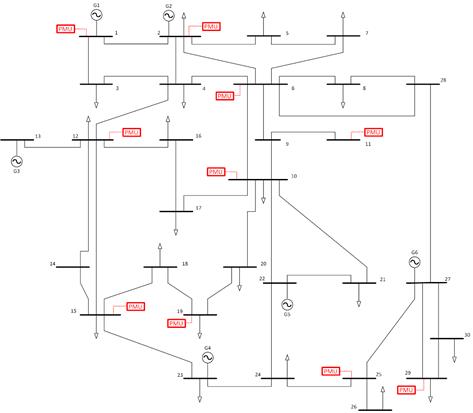
Figura. 1: Ubicación óptima de PMU en el sistema de 30 buses del IEEE sin restricciones de ZIB ni de contingencias.
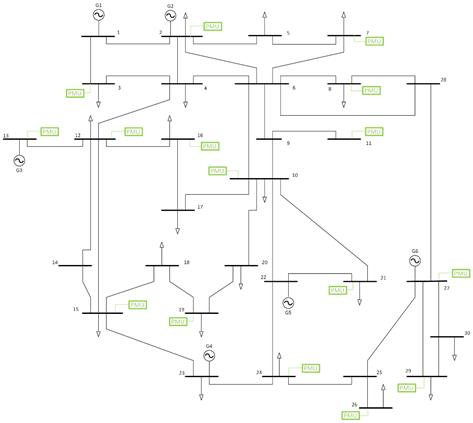
Figura. 2: Ubicación óptima de PMU en el sistema de 30 buses del IEEE con restricciones de ZIB y de contingencias.
Al comparar los resultados mostrados en las Figuras 1y 2, así como los de la Tabla 1, cuando se considera la presencia de contingencias, aumenta la cantidad de PMU que se deben desplegar en el sistema de potencia. Los costos asociados al incremento de PMU en el sistema de potencia se ven justificados en el caso de que algún elemento del SEP salga de la operación; la estimación del estado del SEP se la hará con el 100 % de observabilidad.
En la Tabla 2 se muestran los buses en los que se deben colocar las PMU para cada uno de los casos estudiados, en las cuales se puede apreciar que los ZIB no contienen PMU; debido a la restricción correspondiente.
5. Conclusiones y recomendaciones
Al igual que en la planificación de los sistemas de potencia en donde se considera el concepto de contingencia N-1 para el despliegue óptimo de PMU, también es necesario considerarlo y en el caso de sistemas que ya dispongan de PMU instalados se puede aplicar la metodología propuesta y reubicar las mismas en caso de ser necesario.
Los buses ZIB pueden ser despreciados en los sistemas de potencia en el tema de planificación de ubicación de PMU; con ello la complejidad matemática del análisis se ve reducida.
Las necesidades de la red de comunicaciones y de la capacidad de los servidores, en donde se almacenará la base de datos; son mayores cuando se considera la presencia de contingencias en comparación de cuando no se toma en cuenta dicha restricción.
La metodología planteada para ubicar las PMU en los sistemas de potencia con consideraciones de contingencias N-1, observabilidad del 100 % y redundancia puede ser aplicada tanto para SEP nuevos como para expansiones de los mismos.
