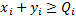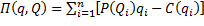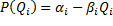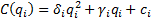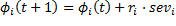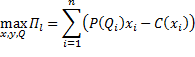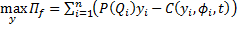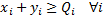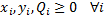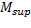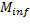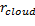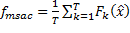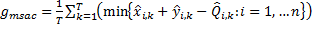1. Introducción
En el ámbito económico varios escenarios de decisión jerárquicos pueden ser modelizados como problemas de competencia de Stackelberg (von Stackelberg, 1952), como parte de la Teoría de Juegos en el ámbito de la Investigación de Operaciones. Específicamente, se trata modelos de optimización de dos niveles (Benoít Colson, Marcotte, & Savard, 2005; Benoît Colson, Marcotte, & Savard, 2007), en los que en una firma líder (asociada a un modelo de optimización superior) tiene por objetivo encontrar la mejor decisión, teniendo en cuenta la reacción óptima de otra firma subordinada (modelo de optimización inferior). Aunque la literatura ha abordado ampliamente los problemas de competencia de Stackelberg, (León & Navarro, 2013; Nakamura, 2015; Nie, 2012; Øksendal, Sandal, & Ubøe, 2013; Wahab, Bentahar, Otrok, & Mourad, 2016; Wang et al., 2016), es importante resaltar que muy pocos estudios asumen que el modelo presenta incertidumbre de algún tipo. En algunos casos, esta incertidumbre pudiera venir dada por la variabilidad en el tiempo de condiciones (decisiones) del adversario (competencia), lo cual es típico de escenarios económicos complejos.
En particular, los problemas de competencia de Stackelberg dinámicos pueden ser abordados desde dos puntos de vista. Por un lado, existen escenarios que pueden ser modelados como problemas de programación dinámica, en los que enfoques clásicos de la Investigación de Operaciones pueden aplicarse sin mayores dificultades. Otra alternativa es asumir que la naturaleza de la dinámica del problema es desconocida, esto es, cómo y cuándo ocurrirán los cambios en el modelo. Obviamente este último enfoque es más general pero debe tener en cuenta una mayor complejidad en el problema. Como consecuencia, los métodos usuales de optimización deben ser adaptados para enfrentar esta incertidumbre. Hasta donde se conoce no existen investigaciones abordando este último enfoque.
Por las razones anteriormente expuestas y con la intención de contribuir a desarrollar este campo de investigación, el presente trabajo tiene por objetivo general: proponer un enfoque computacional evolutivo para la solución de problemas de competencia Stackelberg dinámica. Específicamente, se propone un método metaheurístico (Boussaïd, Lepagnot, & Siarry, 2013) que combina enfoques computacionales evolutivos provenientes de la optimización de dos niveles (Talbi, 2013), y la optimización dinámica evolutiva (Nguyen, Yang, & Branke, 2012).
Para una mejor comprensión de la propuesta, el resto del trabajo queda estructurado de la forma siguiente: en la Sección 2 se describe el modelo que será objeto de estudio y el método de solución desarrollado para resolverlo. La Sección 3 está dedicada a presentar y discutir los resultados obtenidos de los experimentos computacionales realizados. Finalmente, la Sección 4 brinda las conclusiones y trabajos futuros de derivados de la investigación.
2. Materiales y métodos
En la presente sección se describe en detalle el problema a resolver a través de su modelización matemática, y más adelante, el método computacional propuesto.
2.1 Modelo de competencia de Stackelberg dinámica
El modelo de competencia de Stackelberg dinámico que será objeto de estudio en la presente investigación queda establecido informalmente como sigue:
Una firma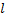 desea maximizar sus ganancias a partir del nivel de producción y nivel de demanda de
desea maximizar sus ganancias a partir del nivel de producción y nivel de demanda de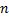 productos, teniendo en cuenta la reacción óptima de un competidor
productos, teniendo en cuenta la reacción óptima de un competidor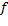 que produce los mismos productos que ésta a lo largo del tiempo. Se asumen conocidas las funciones de ingresos y costos de los productos para ambas compañías.
que produce los mismos productos que ésta a lo largo del tiempo. Se asumen conocidas las funciones de ingresos y costos de los productos para ambas compañías.
Más formalmente el modelo matemático es el siguiente:
Datos:
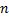 : cantidad de productos que producen tanto la compañía
: cantidad de productos que producen tanto la compañía 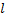 como
como 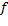 .
.
Se asumen además conocidas las constantes que definen a las funciones de precio de venta y de costo de producción de cada producto (véase más adelante el apartado sobre Funciones objetivo).
Variables de decisión:
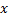 : nivel de producción de los productos de la firma
: nivel de producción de los productos de la firma 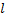 . Donde
. Donde 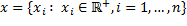 siendo
siendo 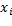 el nivel de producción del producto
el nivel de producción del producto 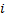 .
.
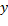 : nivel de producción de los productos de la firma
: nivel de producción de los productos de la firma 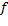 . Donde
. Donde 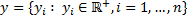 siendo
siendo 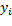 el nivel de producción del producto
el nivel de producción del producto 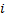 .
.
Restricciones:
Como restricción funcional tendremos la relacionada con el cumplimiento de la demanda para todo producto 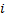 :
:
Adicionalmente se considera que las variables son no negativas, esto es, 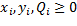 para todo producto
para todo producto 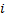 .
.
Finalmente, es importante mencionar que el problema de optimización correspondiente a la compañía competidora 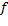 es al mismo tiempo una restricción para el problema principal, esto es, para el modelo correspondiente a la compañía líder
es al mismo tiempo una restricción para el problema principal, esto es, para el modelo correspondiente a la compañía líder 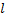 .
.
Funciones objetivo:
De manera general se asumirá que ambas compañías tienen por objetivo maximizar sus respectivos beneficios globales, a partir de la siguiente relación:
donde 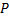 y
y 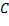 son funciones correspondientes al precio de venta y al costo de producción, respectivamente. Además,
son funciones correspondientes al precio de venta y al costo de producción, respectivamente. Además, 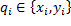 representa el nivel de producción de producto
representa el nivel de producción de producto 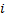 de cada compañía según sea el caso, mientras que
de cada compañía según sea el caso, mientras que 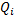 es la demanda del producto
es la demanda del producto 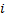 .
.
Aunque las funciones 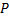 y
y 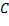 pueden exhibir distintas formas según sea el escenario económico, para los propósitos de la presente investigación será suficiente abordar por cada producto
pueden exhibir distintas formas según sea el escenario económico, para los propósitos de la presente investigación será suficiente abordar por cada producto 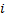 , las siguientes variantes (Sinha, Malo, & Deb, 2014; Sinha, Malo, Frantsev, & Deb, 2014):
, las siguientes variantes (Sinha, Malo, & Deb, 2014; Sinha, Malo, Frantsev, & Deb, 2014):
Donde 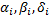 y
y 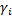 son constantes positivas conocidas, y
son constantes positivas conocidas, y 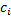 es un costo fijo establecido por la compañía en cuestión.
es un costo fijo establecido por la compañía en cuestión.
En particular consideraremos el escenario en el que los costos asociados a la compañía 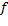 pueden variar en el tiempo. Este dinamismo pudiera tener sus causas en la inestabilidad del mercado y en una estrategia del oponente
pueden variar en el tiempo. Este dinamismo pudiera tener sus causas en la inestabilidad del mercado y en una estrategia del oponente 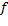 para reaccionar de manera inesperada ante su adversario, que sería la compañía
para reaccionar de manera inesperada ante su adversario, que sería la compañía 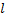 . Concretamente, modelaremos esta cuestión de la siguiente manera. Considere que los costos de la compañía
. Concretamente, modelaremos esta cuestión de la siguiente manera. Considere que los costos de la compañía 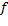 varían en el tiempo de acuerdo a la siguiente regla de transición para cada producto
varían en el tiempo de acuerdo a la siguiente regla de transición para cada producto 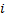 :
:
Siendo 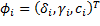 el conjunto de constantes que definen a la función de costos
el conjunto de constantes que definen a la función de costos 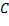 ,
, 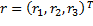 un vector de números aleatorios generados a partir de una distribución normal estándar, y
un vector de números aleatorios generados a partir de una distribución normal estándar, y 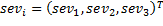 un vector de escalares indicando la severidad de los cambios para cada constante. Es importante notar que otros tipos de cambio para estas constantes son también posibles. Por ejemplo, cambios correlacionados, cíclicos, caóticos, lineales con paso constante, entre otros. Sin embargo, estamos convencidos de que para los propósitos de la presente investigación es suficiente el tipo de cambio definido por la expresión anterior, pues se asume que los cambios siguen una distribución normal, la cual está muy presente en fenómenos reales.
un vector de escalares indicando la severidad de los cambios para cada constante. Es importante notar que otros tipos de cambio para estas constantes son también posibles. Por ejemplo, cambios correlacionados, cíclicos, caóticos, lineales con paso constante, entre otros. Sin embargo, estamos convencidos de que para los propósitos de la presente investigación es suficiente el tipo de cambio definido por la expresión anterior, pues se asume que los cambios siguen una distribución normal, la cual está muy presente en fenómenos reales.
A partir de las consideraciones anteriores queda claro que el modelo a estudiar queda resumido de la siguiente manera:
sujeto a
Si se observa con detenimiento el modelo anterior, el lector podrá apreciar tres características que lo diferencian de los modelos tradicionales de optimización. En primer lugar, que una de las restricciones es al mismo tiempo un problema de optimización, esto es, correspondiente a la compañía 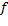 . En segundo lugar, que se trata de un modelo jerárquico en tanto que la compañía
. En segundo lugar, que se trata de un modelo jerárquico en tanto que la compañía 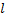 tiene prioridad sobre su competidora
tiene prioridad sobre su competidora 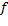 . Esta es precisamente la naturaleza de los modelos de optimización en dos niveles, que no solo incluyen como un caso particular a los de competencia Stackelberg. Finalmente, la presencia de parámetros que varían en el tiempo en la función de costos, convierte al modelo en dinámico.
. Esta es precisamente la naturaleza de los modelos de optimización en dos niveles, que no solo incluyen como un caso particular a los de competencia Stackelberg. Finalmente, la presencia de parámetros que varían en el tiempo en la función de costos, convierte al modelo en dinámico.
Las características antes mencionadas indican que se requieren de métodos especiales para resolver eficientemente este modelo. Una posible variante es abordarlos analíticamente, aprovechando las características de las funciones objetivo y restricciones. Sin embargo, en cuanto el número de variables crece y aparecen funciones no lineales más complejas, ya las técnicas analíticas resultan imposibles o con poca utilidad práctica. Es importante notar que esta complejidad pudiera verse aumentada también por la naturaleza dinámica del problema, la cual se asume desconocida por parte de la compañía 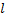 . En ese sentido, la siguiente sección expone el método computacional propuesto, que resuelve de manera aproximada el problema planteado.
. En ese sentido, la siguiente sección expone el método computacional propuesto, que resuelve de manera aproximada el problema planteado.
2.2 Método computacional propuesto
De acuerdo a (Talbi, 2013), desde el punto de vista de métodos metaheurísticos, existen cuatro enfoques para resolver un problema de optimización de dos niveles. El primero es el denominado anidado secuencial, en el que por cada solución candidata del modelo superior se resuelve el modelo inferior. Este enfoque es el más intuitivo si se tiene en cuenta que conceptualmente el modelo indica que, para que una solución cualquiera del modelo superior sea factible, se tiene que resolver el problema inferior. Sin embargo, este enfoque puede resultar excesivamente costoso computacionalmente, por ejemplo en casos donde sea complejo optimizar el problema inferior. De manera alternativa, algunos autores transforman el modelo de dos niveles de manera que pueda ser resuelto por técnicas de optimización tradicionales. Ese es el caso de los enfoques de transformación de un solo nivel y transformación multi-objetivo. No obstante, es importante notar que ambos enfoques asumen que el modelo del problema es conocido explícitamente, y que existe alguna certeza matemática de que tales transformaciones llevan a un problema equivalente, en el que su solución óptima coincide con la del problema original. Finalmente, el cuarto enfoque son los algoritmos coevolutivos, un concepto biológico que ha inspirado a varios autores en el ámbito de la computación evolutiva. La idea detrás de este enfoque es la optimización en paralelo de partes del problema original. En el caso de modelos de dos niveles, se divide el problema en dos subproblemas de optimización, esto es uno por cada nivel, los cuales son resueltos al mismo tiempo. Cada cierto tiempo, una determinada información de los dos procesos de optimización es intercambiada con el objetivo de que la búsqueda sea más exacta, esto es, dirigirla hacia soluciones cercanas a la óptima del problema principal.
Por otro lado, en el caso de la optimización dinámica evolutiva (Cruz, González, & Pelta, 2011; Nguyen et al., 2012), en la literatura se reflejan varias alternativas dependiendo igualmente de las característica del problema, y de la información que asume conocida el investigador. Por lo general predomina la aplicación de metaheurísticas poblacionales (Novoa-Hernández, Corona, & Pelta, 2011; Novoa-Hernández, Pelta, & Corona, 2010). De acuerdo a Jin & Branke, 2005 existen cuatro enfoques principales que se han propuesto en el contexto de las metaheurísticas poblacionales: 1) introducir diversidad después de los cambios, 2) mantener la diversidad durante la ejecución, 3) uso de memorias, 4) enfoques multi-poblacionales. Más recientemente, Nguyen et al., 2012 indica que un quinto enfoque efectivo es el empleo de técnicas auto-adaptativas (Meyer-Nieberg & Beyer, 2007). Estas técnicas dotan de estrategias inteligentes al algoritmo para lidiar con diversos escenarios complejos, minimizando el tiempo de ajuste de parámetros del propio algoritmo por parte del investigador (Novoa-Hernández, Cruz Corona, & Pelta, 2016).
Un análisis sencillo sobre los enfoques mencionados que han sido propuestos para problemas de dos niveles y para problemas dinámicos, nos indica intuitivamente que un método efectivo puede derivarse de la combinación adecuada de técnicas de ambos mundos. Precisamente, en la presente investigación proponemos un algoritmo coevolutivo que incluye una estrategia de diversidad durante la ejecución. Para su concepción se ha tomado en cuenta investigaciones previas como Legillon, Liefooghe, & Talbi (2013); Oduguwa & Roy (2002), para el caso del enfoque de coevolución, y en Blackwell & Branke (2006), para el caso de la estrategia de diversidad durante la ejecución. Además, se ha empleado como paradigma computacional a la Evolución Diferencial (Storn & Price, 1997). Estos tres componentes incluidos en la propuesta han mostrado excelentes resultados en sus respectivos escenarios. Sin embargo, hasta donde se conoce no existen investigaciones que las combinen para resolver problemas de dos niveles dinámicos.
Los pasos generales del algoritmo, que hemos denominado CQDEA (Coevolutionary Quantum Differential Evolution Algorithm), son los siguientes:
Algoritmo CQDEA:
Datos de entrada:
Subalgoritmos 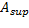 y
y 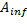 que incluyen Evolución Diferencial y Estrategia de diversidad.
que incluyen Evolución Diferencial y Estrategia de diversidad.
Frecuencia de intercambio de información 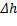 .
.
Paso 1. Crear una población 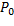 con
con 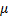 individuos (soluciones candidatas) aleatoriamente siguiendo una distribución uniforme. Inicializar contador de iteraciones
individuos (soluciones candidatas) aleatoriamente siguiendo una distribución uniforme. Inicializar contador de iteraciones 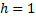 .
.
Paso 2. Inicializar 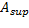 y
y 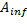 con copias de la población
con copias de la población 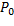 .
.
Paso 3. Detectar cambios en el ambiente mediante la reevaluación de las mejores soluciones de 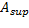 y
y 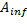 en sus respectivas funciones objetivo. Si se detectan cambios, entonces ir al Paso 4, en caso contrario ir al Paso 5.
en sus respectivas funciones objetivo. Si se detectan cambios, entonces ir al Paso 4, en caso contrario ir al Paso 5.
Paso 4. Reevaluar todas las soluciones en 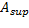 y
y 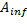 . Ir al Paso 8.
. Ir al Paso 8.
Paso 5. Chequear si es tiempo de intercambiar información 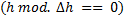 . Si lo es entonces ir al Paso 6, de lo contrario ir al Paso 7.
. Si lo es entonces ir al Paso 6, de lo contrario ir al Paso 7.
Paso 6. Intercambiar la mejor solución entre 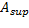 y
y 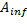 . Primero
. Primero 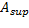 le envía su mejor solución a
le envía su mejor solución a 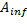 quien distribuye la parte
quien distribuye la parte 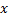 en toda su población y la reevalúa. La mejor solución de
en toda su población y la reevalúa. La mejor solución de 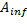 en términos de
en términos de 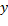 es enviada a
es enviada a 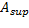 quien la distribuye en su población y la reevalúa. Ir al Paso 8.
quien la distribuye en su población y la reevalúa. Ir al Paso 8.
Paso 7. Actualizar a las población de 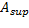 y
y 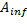 según los pasos del paradigma Evolución Diferencial (Storn & Price, 1997), y la estrategia de diversidad basada en partículas quantum de (Blackwell & Branke, 2006). Actualizar la mejor solución encontrada por
según los pasos del paradigma Evolución Diferencial (Storn & Price, 1997), y la estrategia de diversidad basada en partículas quantum de (Blackwell & Branke, 2006). Actualizar la mejor solución encontrada por 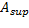 y
y 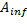 .
.
Paso 8. Chequear si se cumple la condición de parada. Si se cumple, entonces detener la ejecución, si no, incrementar contador de iteraciones (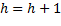 ) e ir al Paso 3.
) e ir al Paso 3.
Es importante resaltar que cuando se dice evaluar o reevaluar una solución se está haciendo alusión no solo al valor correspondiente de la función objetivo, sino también al nivel de cumplimiento de dicha solución en la restricción funcional relacionada con la demanda. En este sentido, el enfoque adoptado por nuestro algoritmo para determinar si una solución es mejor que otra involucrará ambos criterios, esto es, el valor de la función objetivo y el grado de factibilidad según la restricción de la demanda. Concretamente, se ha seguido el enfoque empleado por (Sinha, Malo, & Deb, 2014), y que consiste en los siguientes pasos para comparar dos soluciones:
Paso 1. Si una de las dos soluciones es factible y la otra no, entonces la factible es la mejor. En caso contrario ir al Paso 2.
Paso 2. Si las dos soluciones no son factibles, entonces la mejor es la que tenga un grado de incumplimiento menor en las restricciones. En caso contrario ir al Paso 3.
Paso 3. Si las dos soluciones son factibles, entonces la mejor es aquella con más calidad de acuerdo a su valor en la función objetivo.
3. Resultados y discusión
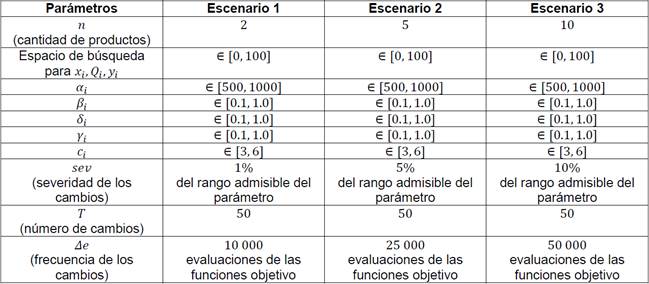
Con el objetivo de analizar y evaluar el método propuesto en la sección anterior, en lo que sigue se describirán los resultados obtenidos a partir de los experimentos computacionales realizados. Para simular algunas situaciones reales se consideraron los escenarios mostrados en la Tabla 1, que corresponden al modelo a resolver.
Tabla 1 Escenarios del problema de competencia Sctackelberg dinámico considerados en los experimentos.
Como principal medida de rendimiento se seleccionó la media de la calidad (valor de la función objetivo) de la mejor solución del algoritmo antes del cambio (Novoa-Hernández et al., 2011, 2010). La fórmula matemática correspondiente a esta medida es la siguiente:
Donde 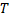 es la cantidad de cambios que experimentará el ambiente,
es la cantidad de cambios que experimentará el ambiente, 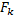 es la función objetivo en el ambiente
es la función objetivo en el ambiente 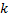 , y
, y 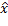 es la mejor solución obtenida por el algoritmo antes de ocurrir el cambio
es la mejor solución obtenida por el algoritmo antes de ocurrir el cambio 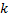 . Es importante destacar que, dado que el modelo que nos ocupa está orientado a maximizar las ganancias, un valor alto de la medida anterior indicará un buen rendimiento para el algoritmo, y un bajo rendimiento en caso contrario. Adicionalmente hemos considerado una medida para determinar el nivel de cumplimiento de la restricción funcional del modelo. De manera similar a la expresión anterior, se agrupará este nivel de incumplimiento a través de la media:
. Es importante destacar que, dado que el modelo que nos ocupa está orientado a maximizar las ganancias, un valor alto de la medida anterior indicará un buen rendimiento para el algoritmo, y un bajo rendimiento en caso contrario. Adicionalmente hemos considerado una medida para determinar el nivel de cumplimiento de la restricción funcional del modelo. De manera similar a la expresión anterior, se agrupará este nivel de incumplimiento a través de la media:
Donde 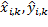 y
y 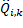 son las
son las 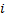 -ésimas componentes de la mejor solución del algoritmo antes del cambio
-ésimas componentes de la mejor solución del algoritmo antes del cambio 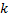 . En este caso, un valor negativo indica que se incumple con la restricción, mientras que uno positivo o igual a cero que se cumple.
. En este caso, un valor negativo indica que se incumple con la restricción, mientras que uno positivo o igual a cero que se cumple.
En relación al algoritmo propuesto, se consideraron las variantes mostradas en la Tabla 2, las cuales fueron derivadas de las combinación de parámetros cruciales para el enfoque coevolutivo, y para el enfoque de diversidad durante la ejecución. Estos son la frecuencia de intercambio de información entre los subalgoritmos (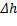 ), y el radio de diversidad de la estrategia propuesta por (Blackwell & Branke, 2006).
), y el radio de diversidad de la estrategia propuesta por (Blackwell & Branke, 2006).
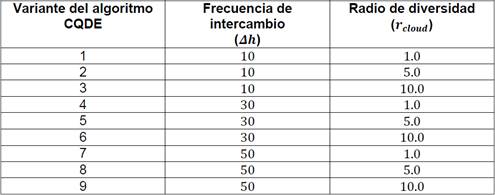
Tabla 2 Variantes del algoritmo propuesto según los valores de tiempo de intercambio y radio de diversidad.
En sentido general se realizaron 30 ejecuciones (simulaciones) por cada par problema-algoritmo. En cada una con semillas aleatorias diferentes. La plataforma empleada fue el software Matlab 2015b, en una PC con 8 GB de RAM y procesador Intel i5 a 2.7 GHz.
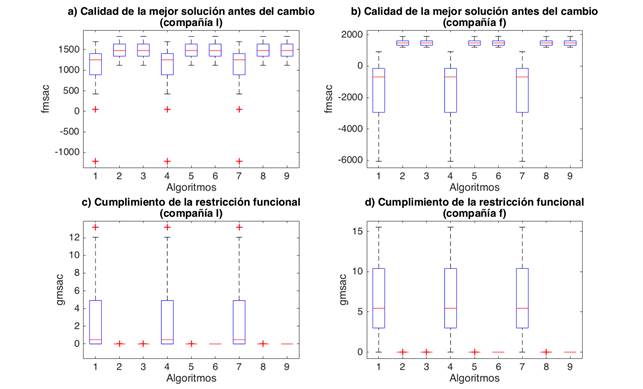
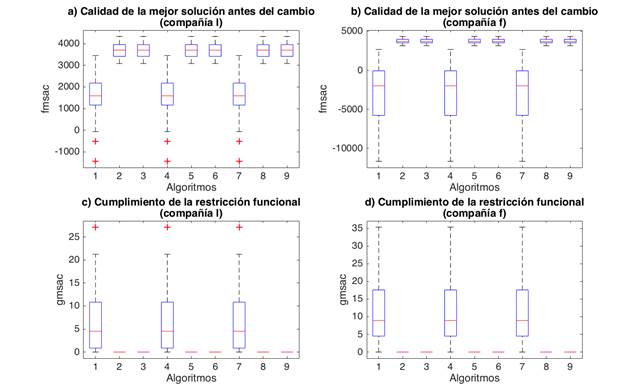
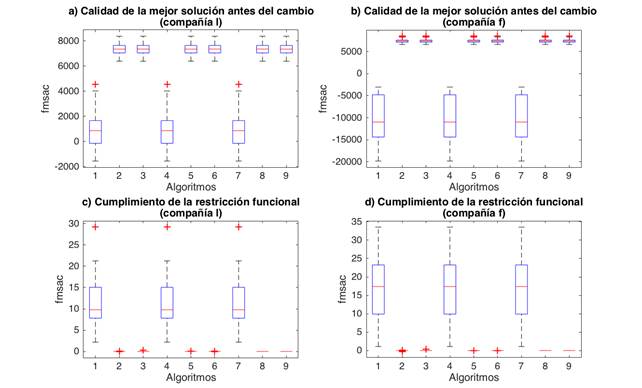
Los resultados obtenidos se resumen en las figuras 1, 2 y 3, a través de gráficos de caja, para los escenarios 1, 2 y 3, respectivamente. En cada figura se ha incluido la calidad y el grado de cumplimiento de la restricción funcional del problema, para ambos submodelos. Por ejemplo, los gráficos a) y b) de las figuras 1, 2 y 3, corresponden a la media de la calidad de la mejor solución antes del cambio obtenida en el modelo superior (compañía l), y en el modelo inferior (compañía f), respectivamente. Similarmente, los gráficos c) y d) de las figuras mencionadas, corresponden a la media del grado de cumplimiento en la restricción funcional para la mejor solución antes del cambio, en el modelo superior e inferior, respectivamente.
Observe que en las tres figuras aparecen patrones similares en cuanto al rendimiento de los nueve algoritmos. En particular se aprecia que las variantes 1, 4 y 7 son las que peor resultados exhiben. Esto indica que el radio de diversidad igual a 1.0 no resulta suficiente para lidiar con los efectos producidos por los cambios. En contraste con estos resultados, el resto de las variantes muestran un mejor rendimiento al emplear un radio de diversidad mayor.
Observe que las mejores variantes, esto es 2, 3, 5, 6, 8 y 9, también exhiben una menor dispersión en los resultados en comparación con las variantes 1, 3, y 7. Esto es fácilmente apreciable a partir de las dimensiones de las cajas. Otro aspecto a destacar en relación a la calidad de los algoritmos es que como tendencia general, se observa que esta tiende a degradarse para las variantes 1, 3, y 7, conforme aumenta la complejidad del problema. Esta afirmación se puede verificar comparando los gráficos a) y b) de las figuras 1, 2, y 3, para las variantes mencionadas. Como resultado se podrá apreciar un estancamiento en el valor de la media, y la presencia de valores muy inferiores de calidad, incluso negativos.
En relación al grado de cumplimiento de la restricción funcional (gráficos c) y d) de las figuras 1, 2, y 3), el lector puede apreciar que todos los algoritmos mantiene valores no negativos en los resultados. Esto indica que todas las variantes obtuvieron soluciones factibles. Sin embargo, es importante destacar que los valores correspondientes a las variantes que peor calidad poseen (1, 4, y 7) son en su mayoría superiores a 0, mientras que en el resto la tendencia es acercarse a 0.
Para confirmar las afirmaciones anteriores, y determinar más específicamente cuál o cuáles variantes son las mejores, se aplicaron pruebas estadísticas no paramétricas, de acuerdo a lo sugerido por García, Molina, Lozano, & Herrera (2009). En este sentido, los datos empleados para las pruebas fueron los resultados en términos de 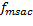 en todas las ejecuciones, y agrupándolas en modelo superior, modelo inferior, y ambos modelos.
en todas las ejecuciones, y agrupándolas en modelo superior, modelo inferior, y ambos modelos.
Primeramente, se aplicó la prueba de Friedman para determinar si existían diferencias a nivel de grupo, y al mismo tiempo determinar un ordenamiento (ranking) promedio de las variantes. Los p-valores correspondientes a esta prueba para los tres conjuntos de datos mencionados fueron menores que 0.05, mientras que las posiciones promedio son las mostradas en la Tabla 3. Obsérvese que la mejor variante es la 5 aunque no difiere mucho su posición en relación a 2, 3, 6, 8 y 9. Sin embargo, esta sí se diferencia de manera apreciable si se compara con las variantes 1, 4, y 7, esto es, las de peor calidad.
A partir del resultado obtenido en la prueba anterior, se procedió con una prueba de Holm para determinar si existen diferencias con respecto a la mejor variante. En la Tabla 3 se puede apreciar que las suposiciones anteriores quedan confirmadas por la prueba de Holm. Esto es, aquellas variantes con posiciones medias cercanas a la mejor, no son significativamente diferentes a esta; mientras que el resto sí lo son.
Tabla 3 Resultados de las pruebas estadísticas de Friedman y Holm (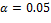 ) para las variantes del algoritmo CQDE, en relación a la calidad del modelo superior, modelo inferior, y ambos modelos.
) para las variantes del algoritmo CQDE, en relación a la calidad del modelo superior, modelo inferior, y ambos modelos.
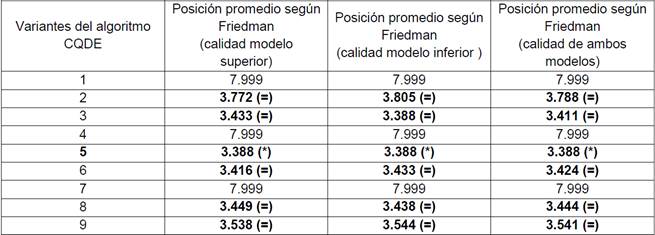
(*) Mejor variante, (=) Variante con diferencias no significativas con respecto a la mejor variante, según la prueba de Holm.
4. Conclusiones y recomendaciones
En este trabajo se abordó la solución del problema de competencia Stackelberg en su versión dinámica. Dada la incertidumbre presente en el modelo considerado se propuso un método computacional basado en enfoques de la optimización en dos niveles, y de la optimización dinámica evolutiva. Los resultados de los experimentos revelan que el método propuesto resuelve de manera efectiva tres escenarios del problema objeto de estudio. Especialmente, cuando un parámetro de la estrategia de diversidad aplicada, se hace cercano en magnitud a la severidad del problema.
Como trabajos futuros se planea analizar y proponer medidas de rendimiento más efectivas en la evaluación de algoritmos metaheurísticos en problemas de optimización de dos niveles dinámicos. Además, la aplicación de enfoques auto-adaptativos que minimicen el esfuerzo del investigador en establecer parámetros tan influyentes como el radio de diversidad. Existen evidencias de que estos enfoques contribuyen significativamente en el rendimiento del algoritmo durante la ejecución (Novoa-Hernández, Corona, & Pelta, 2013).
Finalmente, es conveniente mencionar que el código fuente relacionado con los experimentos desarrollados en esta investigación estará disponible para su uso por parte de la comunidad científica a través de la red ResearchGate , y a través de solicitud por correo electrónico a los autores. Con esta acción deseamos motivar el interés por el estudio de este problema económico-matemático en la comunidad científica.