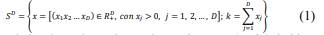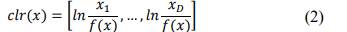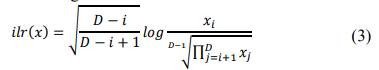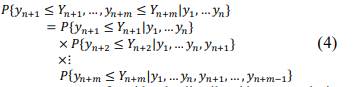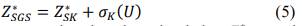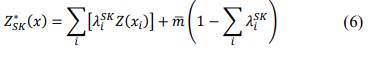1. INTRODUCCIÓN
(Lishchuk & Pettersson, 2021); sin embargo, esta fase implica un riesgo significativo de las inversiones mineras, tomando en cuenta que 1 de cada 100 zonas exploradas presenta un potencial económico para su explotación (Pachas, 2014). En este entorno, también son frecuentes los impasses políticos y socioambientales; estos aspectos incluso han hecho que varios países se interesen por el desarrollo de la exploración minera espacial (Hickson et al., 2020; Wouters et al., 2021), no obstante, es evidente que la única fuente de estos recursos a corto, mediano y largo plazo es nuestro planeta, por lo cual, esta fase inicial de la minería es una de las más importantes. Ecuador presenta un gran potencial minero, donde principalmente existe interés común por los metales preciosos como el Oro (Au) y la Plata (Ag), y metales base desde las fases de exploración hasta la explotación de estos recursos. En tal sentido, es notorio que otros elementos traza y Tierras Raras (REE) simplemente son estudiados como indicadores geoquímicos (IG), a pesar de que en varios yacimientos pueden representar un valor económico equivalente para la industria metalúrgica, lo que limita su aprovechamiento; debido a que países importadores de concentrado como China, Alemania, Estados Unidos y Japón, obtienen un valor agregado de estos elementos, además, penalizan de manera económica el Cd, As, Pb, etc. (Gulley et al., 2018). Adicionalmente, es fundamental tener en cuenta la presencia de elementos perjudiciales en los procesos metalúrgicos de recuperación, ya que influyen negativamente en la rentabilidad de proyectos mineros; por lo cual, integrar aspectos metalúrgicos desde la exploración minera reduce el riesgo, sin embargo, esto no forma parte de los estudios actuales (Ghasemzadeh et al., 2019; Habib et al., 2019).
Ante esto, la geología, minería y metalurgia se han integrado en una ciencia denominada geometalurgia, cuyo objetivo es maximizar el valor económico de un proyecto, minimizar el riesgo técnico, generar una operación más resiliente desde su fase exploratoria y comprender la variabilidad de sus atributos geometalúrgicos (AG) a partir de muestras distribuidas espacialmente (Dominy et al., 2018). En tal sentido, los AG son cualquier propiedad de la roca que influye de manera positiva o negativa en el valor de un recurso mineral (Ramos & Calderón, 2022). Se clasifican en primarios y de respuesta o secundarios (Coward et al., 2009). Los AG primarios son propiedades de la roca medidas de forma directa, por ejemplo, ley mineral, alteración, concentración de indicadores geoquímicos y/o de elementos perjudiciales en los procesos metalúrgicos (Ramos & Calderón, 2022); mientras que, los AG secundarios se expresan como respuesta a un proceso o aplicación de energía, por ejemplo: recuperación metalúrgica, consumo de reactivos, moliendabilidad (Coward et al., 2009). En la etapa exploratoria la geoquímica, es fundamental en la localización de elementos y minerales de interés geoeconómico-metalúrgico, no obstante, las técnicas tradicionalmente utilizadas en la actualidad para el procesamiento de los datos presentan ciertas limitantes. En tal sentido, existen importantes investigaciones sobre las técnicas estadísticas avanzadas como el Análisis Composicional (CoDa) propuesto por Aitchison (1986), el cual se busca reducir la dimensionalidad de un conjunto de datos cerrados para evaluar sus D partes y sus Componentes Principales (PC) por medio de transformaciones log-ratio aditiva (alr), log-ratio centrada (clr) y log-ratio isométrica (ilr) (Egozcue et al., 2003). Los recursos auríferos en la corteza terrestre son una fuente agotable, en ese sentido, la exploración es cada vez mayor.
Por lo cual, en los trabajos realizados por Zhou et al. (2020), Zuo (2021) y Zheng et al. (2023) en zonas prospectivas de China se han obtenido resultados de anomalías geoquímicas que se correlacionan positivamente con datos de yacimientos conocidos, no obstante, estos estudios se enfocan en la evaluación de IG y no consideran el concepto geometalúrgico. A pesar de esto, en algunas zonas mineralizadas se cuenta con cierta información metalúrgica durante la prospección, por ejemplo, el estudio realizado por Ichau (2019) quien ha considerado la información de una zona con potencial geológico-minero ubicada en Ecuador, enfocada en la recuperación de Oro mediante lixiviación en muestras correspondientes a un cuerpo vetiforme, del cual su balance metalúrgico indica una ley de 57.45 g/t Au y recuperación mayor al 90 %. A lo largo de dicha zona, también es prominente la investigación científica realizada por Álvarez y Lovera (2022), en la cual los autores obtuvieron resultados positivos respecto a la correlación entre planos de anomalías y datos de depósitos ubicados en la zona de estudio, no obstante, las estimaciones se elaboraron por medio de Kriging Ordinario (OK), cuya limitante es el suavizamiento de la realidad del fenómeno.
En este aspecto, existen técnicas estocásticas como la simulación geoestadística que consiste en obtener varias realizaciones para reproducir las estadísticas de la data original respetando su variabilidad espacial (Narciso et al., 2019) y una representación no suavizada de la realidad. En este contexto, se cuenta con la simulación secuencial gaussiana de tipo condicional que requiere distribución normal en las muestras, es decir, con media 0 y varianza 1 (Abzalov, 2016).
Por lo tanto, el objetivo de esta investigación es realizar la simulación geometalúrgica para la exploración de ocurrencias minerales de Oro y Plata, a través de la integración de información geológica, geoquímica y de elementos perjudiciales en la lixiviación, mediante análisis CoDa con la finalidad de conformar grupos multivariables de elementos y la aplicación de técnicas geoestadísticas estocásticas para el procesamiento del conjunto de datos geoquímicos de 37 elementos en 448 muestras de sedimentos fluviales provenientes de una zona prospectiva ubicada al NW del Ecuador.
2. METODOLOGÍA
2.1 Ubicación y Contexto Geológico del Área de Estudio
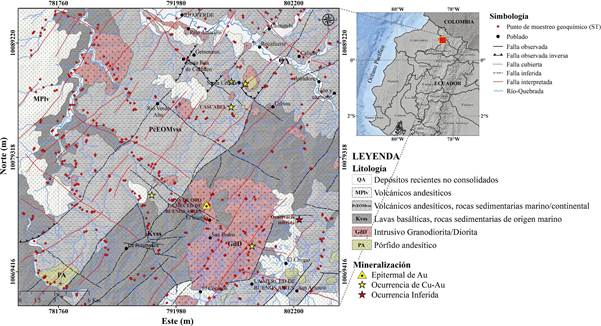
La zona prospectiva se ubica al NW del Ecuador en la Provincia de Imbabura, entre los poblados de La Merced de Buenos Aires al S y Río Verde al N (Figura 1). Presenta un basamento de corteza oceánica acrecionada al continente predominado por lavas basálticas y rocas sedimentarias de origen marino de edad Cretácica (Kvss), están sobreyacidas por rocas sedimentarias marino/continentales y por grupos volcánicos andesíticos de la actividad volcánica transicional del Paleoceno, Eoceno y del Mioceno (PcEOMvss - MPlv), completan la columna estratigráfica los depósitos recientes no consolidados del Cuaternario (QA) (Boland et al., 2000; Vallejo et al., 2019). Asimismo, destaca la presencia de cuerpos intrusivos Granodioríticos/Dioríticos (GdD) y porfiríticos andesíticos (PA) producto del magmatismo del terciario (Boland et al., 2000); la mineralización metalífera se asocia directamente a estos cuerpos magmáticos, la cual también se relaciona con zonas de debilidad producto de la interacción entre el sistema de fallas principal con rumbo NESW y el sistema de fallas secundario (Álvarez & Lovera, 2022).
2.2 Tratamiento de Datos Geoquímicos
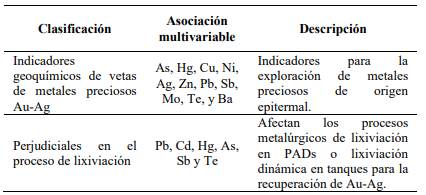
Inicialmente, se elaboró la normalización del conjunto de datos geoquímicos de 37 elementos (medidos en ppm) correspondientes a las 448 muestras (Data disponible en https://github.com/GeologicalSciences/GEOCHEMICALDATABASE), lo cual consistió en dividir a los elementos Zn, Ni, Ti, Ba, Cd, Co y la ∑ 𝑅𝑅𝑅𝑅𝑅𝑅 (elementos Itrio y Escandio) para el Fe, y los elementos Pb, Hf, Th, Te, Mo, y ΣREE para el Mn; ya que estos dos elementos cuando precipitan en la naturaleza como Óxidos o Hidróxidos tienden a atrapar cationes metálicos debido a su alto potencial Óxido-Rédox, lo que puede originar anomalías erráticas (Chao y Theobald, 1976; Hein et al., 2013). Luego, se realizó su análisis composicional definiendo dos grupos multielementales, el primero de IG de vetas de metales preciosos para Au, Ag y el segundo de elementos perjudiciales en el proceso de lixiviación. Finalmente, se elaboró la simulación para ambos grupos y la probabilidad de ocurrencia en cada uno de ellos.
2.3 Análisis Composicional (CoDa)
Un conjunto de datos cerrados como los geoquímicos son vectores aleatorios, que en términos estadísticos sus componentes se representan en un espacio muestral denominado Simplex (𝑆𝑆) (Aitchison, 1986; Egozcue et al., 2003), dichos vectores equivalen a proporciones, porcentajes (%) o partes por millón (ppm), para su tratamiento se aplica el principio de escalabilidad invariable, por lo cual, los datos composicionales viven dentro del Simplex debido a la restricción de la sumatoria constante (k) de las D partes; por lo tanto, si se trabaja en % la suma equivale a 1 y si es en ppm la suma equivale a 106 (Oñate, 2018). En tal sentido, en el Simplex (𝑆𝐷) = 𝑅+ 𝐷-1 se reduce la dimensionalidad en D-1 con respecto al espacio euclidiano real (𝑅+) y está definido por:
donde los datos de x solo pueden variar entre 0 y k (Aitchison, 1986), por lo cual, se entiende que si dos partes se mueven de forma proporcional dentro del Simplex, su relación se mantiene constante y el logaritmo de dicha relación tiene varianza cero:
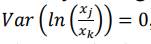 , como resultado se obtiene una matriz de variación cuadrada (j=1, 2,…, D; k=1, 2,…, D). En este contexto, se tiene las trasformaciones log-ratio aditiva (alr), log-ratio centrada (clr) y log-ratio isométrica (ilr), las cuales se basan en el principio del Simplex (Jones & Aitchison, 1987). Las transformaciones más aplicadas en el campo científico son clr e ilr debido a que la transformación alr carece de simetría, por lo tanto, no permite representar las coordenadas producto de la transformación D-1 dentro de los ejes ortogonales (Egozcue et al., 2003). La transformación clr está representada por:
, como resultado se obtiene una matriz de variación cuadrada (j=1, 2,…, D; k=1, 2,…, D). En este contexto, se tiene las trasformaciones log-ratio aditiva (alr), log-ratio centrada (clr) y log-ratio isométrica (ilr), las cuales se basan en el principio del Simplex (Jones & Aitchison, 1987). Las transformaciones más aplicadas en el campo científico son clr e ilr debido a que la transformación alr carece de simetría, por lo tanto, no permite representar las coordenadas producto de la transformación D-1 dentro de los ejes ortogonales (Egozcue et al., 2003). La transformación clr está representada por:
Donde la función 
Donde 𝑥1, 𝑥2, … , 𝑥𝐷 son las variables disponibles y 𝑥𝑗 es la variable estudiada. 𝐷 es el número de variables e 𝑖 es el número de variables estudiadas. El denominador es la raíz total de todas las variables (excepto la variable en el numerador).
2.4 Simulación Secuencial Gaussiana (SGS)
Es un algoritmo ampliamente utilizado para la caracterización estocástica de propiedades en diversas disciplinas de ciencias de la tierra (Manchuk & Deutsch, 2012) y especialmente en geometalurgia (Hosseini & Asghari, 2015) de tipo condicional que permite obtener múltiples realizaciones de la variable en estudio. El principio de la simulación secuencial se basa en la factorización de la probabilidad conjunta (𝑃) de un conjunto de m variables aleatorias (𝑅V), 𝑌, y 𝑛 datos condicionantes (Ecuación 4) (Manchuk & Deutsch, 2012). El conjunto de 𝑚 variables aleatorias puede representar los nodos de una cuadrícula que discretiza el domino a modelar, o podría representar varios atributos diferentes en la misma ubicación, o una combinación de estos.
Cada componente es una función de distribución acumulativa condicional (ccdf). Si estos se pueden calcular, entonces la simulación de los valores 𝑦𝑖, 𝑖 = 𝑛 + 1 … 𝑛 + 𝑚, se logra extrayendo secuencialmente una muestra aleatoria de cada ccdf. El conjunto de todos los valores extraídos comprende una realización de la función aleatoria 𝑌. Cuando esta función es gaussiana, la ccdf se determina mediante Kriging Simple (𝑆K) y el valor simulado se establece por medio de la Ecuación 5 (Abzalov, 2016).
Donde 𝑍SGS ∗ corresponde al valor simulado, 𝑍SK ∗ es la estimación por Kriging Simple, 𝜎𝜎𝐾𝐾 es la desviación estándar de estimación por Kriging y 𝑈 una función normal aleatoria. Cabe notar que la Simulación Secuencial Gaussiana se aplica a funciones aleatorias normales, sin embargo, generalmente las variables geometalúrgicas no tienen distribución simétrica (Adeli, 2018), por lo tanto, previamente debe efectuarse su anamorfosis gaussiana. En lo referente al 𝑆K, se utiliza para calcular las ccdfs para SGS, que requiere conocer el valor medio m de la variable en estudio, expresado a través de la Ecuación 6 (Abzalov, 2016).
Donde 𝜆𝑖 sk son los pesos de 𝑆K asignados a cada dato 𝑍(𝑥i). La 𝑆GS implica modelar variogramas para establecer direcciones de anisotropía y el desempeño del modelo se evalúa por medio de validación cruzada “dejando uno fuera” (Ekolle et al., 2022) y también de tipo jackknife (Rossi & Deutsch, 2014), procurando que el coeficiente de correlación en su gráfico de dispersión entre valores predichos y reales sea cercano a 1 y que su histograma de errores tienda a un comportamiento simétrico.
3. RESULTADOS Y DISCUSIÓN
3.1 Análisis Composicional y Definición de Grupos Multielementales
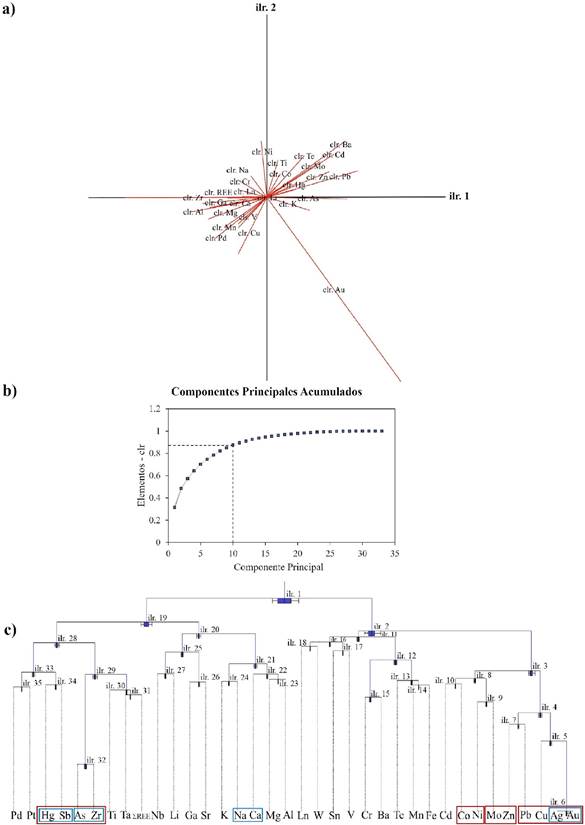
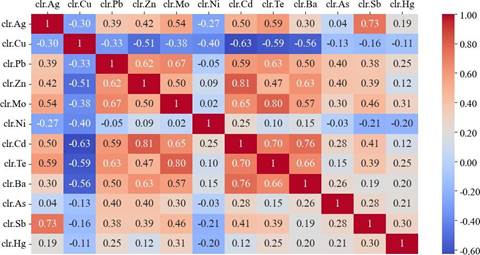
Para realizar un análisis geoestadístico con datos geoquímicos, es necesario convertirlos a un sistema abierto (Talesh et al., 2018) en el cual, los elementos sean independientes entre sí, lo que permite hacer el análisis de las D partes de un todo dentro del Simplex para la conformación de grupos multivariables y de sus Componentes Principales (PC). Por lo tanto, el Análisis Composicional elaborado con el software CoDaPack, ha permitido la representación vectorial de los 37 elementos geoquímicos en un biplot (Figura 2a) después de pasar de unidades en ppm a valores adimensionales transformados mediante clr y/o ilr, donde es posible interpretar que los vectores con mayor longitud tales como el Au y el Zr aportan con mayor información en este estudio y los vectores con cierta perpendicularidad tienen una mejor correlación, en tal sentido, se tiene que el Au se correlaciona con elementos como el Cu, Ag, Zn, Hg, Ba, Te, Mo, entre otros; lo que ha permitido inferir los IG más representativos. Asimismo, en la Figura 2b correspondiente a los Componentes Principales Acumulados, se han definido como más representativas las 10 primeras clases, dado que a partir de estas la curva tiene un comportamiento asintótico. En este contexto, se tienen relaciones multielementales a saber, Ni/Au, Ni/Hg, Pb/As y Pb/Hg definidas como indicadores geoquímicos de vetas de Au-Ag y/o perjudiciales en los procesos de recuperación metalúrgica. Adicionalmente, cabe mencionar el análisis correlacional (coeficiente de Pearson Rho entre 0 y 1) para los elementos que conforman los grupos multielementales (ver Anexo 1), donde los valores > 0.5 matemáticamente son los más representativos, por ejemplo, el Pb tiene un Rho de 0.6 con respecto al Zn definidos como IG de metales preciosos/base, el Rho de 0.6 entre el Pb y Cd como elementos perjudiciales en el proceso de lixiviación de Au. Además, se ha representado el dendrograma de clústeres (Figura 2c) donde es prominente la conformación de grupos y subgrupos, tales como el Cu-Au-Ag que responde a elementos de interés económico, el grupo del Hg, Sb y As que se interpretó como indicadores geoquímicos de Au-Ag, y el subgrupo conformado por el K-Na que indican procesos metasomáticos de mineralización. Este análisis se ha complementado con la interpretación de los Componentes Principales, análisis correlacional de Pearson y datos bibliográficos para IG propuestos por Korshunova y Charykova (2019) y de elementos perjudiciales en el proceso de lixiviación recomendado por Lane et al. (2016). Esto permitió seleccionar 12 de los 37 elementos para definir los grupos multielementales indicados en la Tabla 1.
3.2 Simulación Geometalúrgica
3.2.1 Análisis Exploratorio de Datos y Anamorfosis Gaussiana
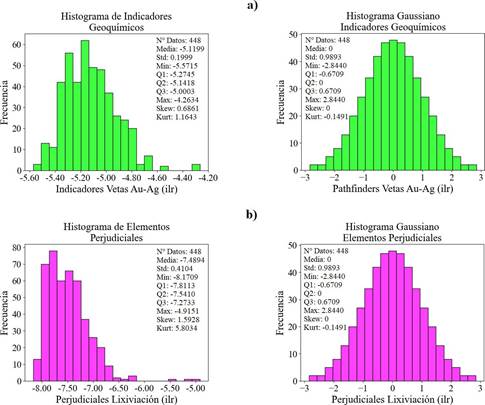
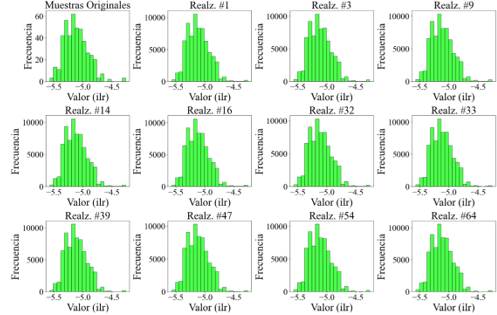
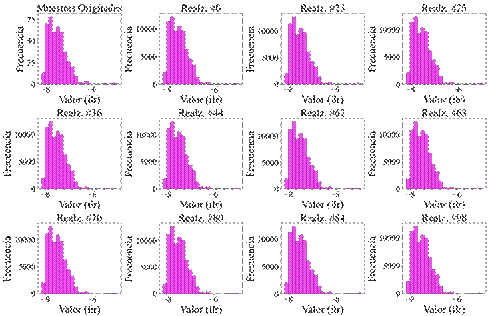
Las estadísticas descriptivas e histogramas de las 448 muestras en cada grupo multielemental se ilustra en la Figura 3. Para indicadores geoquímicos (Figura 3a), su media es -5.1199 con desviación estándar (Std) igual a 0.1999 y valor mínimo de -5.5715; el primer, segundo y tercer cuartil (Q) es -5.2745, -5.1418, -5.0003 respectivamente, mientras que, el valor máximo es de -4.2634; el coeficiente de asimetría (Skew) es igual a 0.6861, en consecuencia, su distribución es asimétrica positiva y al tener curtosis (Kurt) de 1.1643 se trata de un histograma leptocúrtico. Por otro lado, para elementos perjudiciales (Figura 3b) su media es -7.4894 y desviación estándar igual a 0.4104 con valor mínimo de -8.1709; su primer, segundo y tercer cuartil es -7.8113, -7.5410 y -7.2733 respectivamente, en tanto que, su valor máximo igual a -4.9151; el coeficiente de asimetría es igual a 1.5928, por ende, su distribución es asimétrica positiva al estar la mayor cantidad de muestras agrupadas a la izquierda y al ser su curtosis mayor a 0 el histograma es leptocúrtico. Debido a que las muestras no siguen una distribución normal fue necesario aplicar anamorfosis gaussiana en ambos casos, ya que la SGS requiere que los valores tengan distribución simétrica, es decir, con media 0 y varianza 1 (Abzalov, 2016).
3.2.2 Modelamiento Variográfico
Para encontrar direcciones de anisotropía se modelaron variogramas de tipo exponencial (Figura 5) con las muestras transformadas en el software SGeMS. El área de búsqueda es elíptica, en donde la dirección principal del variograma que contiene el alcance máximo representa el eje mayor de la elipse y la dirección secundaria perpendicular a este es el eje menor. El número de lags son 12, separación de lag 1 200 m y tolerancia de lag 600 m. La búsqueda consideró 8 direcciones, inicialmente en azimut 0° con intervalos de 22.5° hasta 157.5° y buzamiento de 0° en todos los casos; la tolerancia angular es 22.5° y el ancho de banda 2.5 m. El efecto pepita y meseta es 0.25 y 0.5 en indicadores geoquímicos, mientras que en perjudiciales es 0.3 y 0.7
Para evaluar los modelos variográficos se aplicó la validación cruzada dejando uno fuera “LOOCV” y jackknife (Figuras 4 y 5). En LOOCV cada muestra observada se elimina de forma sucesiva del conjunto total de datos y una nueva es predicha en ese lugar; de esta manera la diferencia entre la muestra predicha y observada indica hasta qué punto el valor de las muestras es ajustada a la vecindad de datos cercanos. Mientas que, la técnica jackknife tiene como objetivo remuestreo sin reemplazo cuando se vuelve a predecir valores de datos alternativos a partir de otro conjunto de datos que no se superpone. Para lo cual, Abildin et al. (2019) recomiendan dividir aleatoriamente el número total de muestras en dos partes, considerando el 80 % para modelamiento variográfico y el 20 % para su validación (Figura 4), valores sugeridos por Battalgazy et al. (2023) y Gholamy et al. (2018).
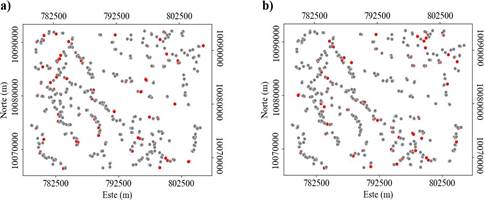
Figura 4 Visualización de muestras para modelo variográfico (gris) y de análisis jackknife (rojo). a) Indicadores geoquímicos. b) Elementos perjudiciales. Se ilustra que, al realizar la división del conjunto de datos en cada grupo multielemental se han obtenido 358 muestras (80 %) para elaborar el modelo variográfico y las 90 muestras (20 %) restantes que no serán consideradas para esto, se utilizarán para su reestimación y evaluar la calidad del modelo
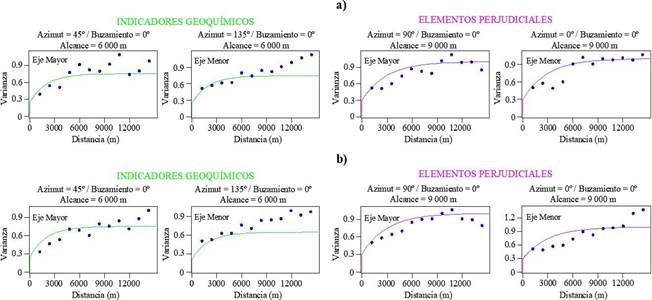
Figura 5 Variogramas experimentales (azul) y ajustados a modelo exponencial. a) LOOCV - El modelo de variograma considera el conjunto total de datos correspondientes a 448 muestras. b) Jackknife - Toma en cuenta para el modelamiento variográfico únicamente el 80 % del total de datos, es decir, 358 muestras
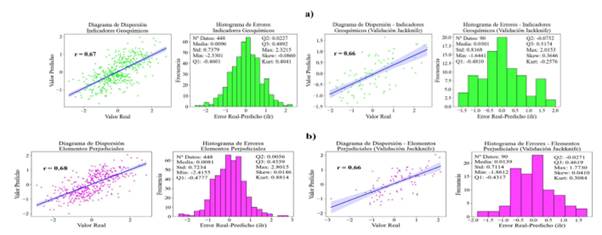
De acuerdo con los resultados obtenidos en la Figura 5, se aprecia que, tanto para IG como para elementos perjudiciales el modelamiento variográfico es isotrópico. Además, el diagrama de dispersión (Figura 6) entre valores reales 𝑧(𝑥𝛼) y predichos 𝑧∗(𝑥𝛼) muestra resultados similares entre LOOCV y jackknife, con coeficiente de correlación (r) mínimo de 0.66; asimismo, en ambos casos se establece que el histograma de errores tiene distribución simétrica, por lo tanto, se corrobora que la media de errores es 
3.2.3 Multielementales
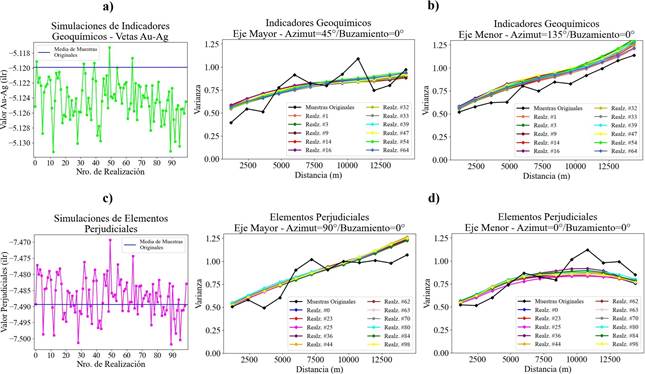
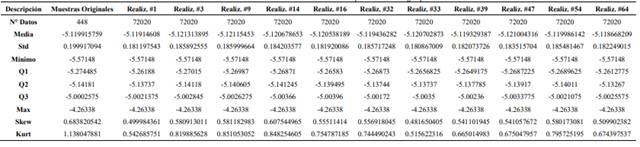
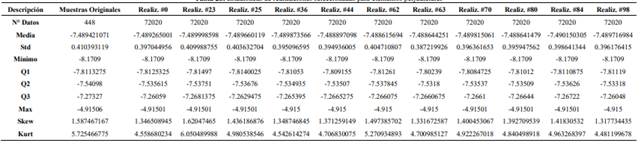
Para elaborar la SGS se configuró en el software SGeMS la grilla bidimensional sobre la cual se efectuaron las realizaciones. El tamaño de cada celda es de 100 m * 100 m; sus límites mínimo y máximo en el eje Este son 778 500 m y 806 200 m respectivamente, mientras que, en el eje Norte 1 006 6300 m y 1 009 2300 m. Por lo tanto, se simularon 72 020 celdas con las muestras transformadas y se generaron 100 realizaciones para cada grupo multielemental, al ser este valor recomendable para la SGS de variables geometalúrgicas (Goovaerts, 1999; Hosseini & Asghari, 2015); después de la simulación, las muestras de cada grupo se volvieron a transformar a sus valores iniciales mediante anamorfosis inversa. Luego fueron seleccionadas las 11 realizaciones (Figura 7 y Anexos 2, 3) que más se vinculan a los datos de muestreo. Desde el punto de vista estadístico para indicadores geoquímicos y elementos perjudiciales, las realizaciones óptimas que reproducen mejor la media (Figuras 7a, 7c y Anexo 2) e histogramas (Anexo 3) de muestras originales son la #54 y #25 respectivamente. En tanto que, bajo un enfoque geoestadístico el análisis entre variogramas de realizaciones óptimas en ambos grupos (Figuras 7b y 7d) muestra que su reproducción es adecuada en comparación a los variogramas de datos originales. La Figura 8 ilustra los mapas obtenidos para los dos grupos multielementales.
3.3 Discusión
En la Figura 7a correspondiente a la Realización #54, se evidencian zonas con valores superiores a -4.4 (ilr) que se interpretan como zonas anómalas para elementos indicadores de depósitos de Oro y Plata, sin embargo, con la finalidad de definir de manera optimista estas anomalías se ha determinado la probabilidad al considerar valores superiores a -4.05 (ilr) (Figura 7c) en base a la clasificación de anomalías de IG de vetas de Au-Ag del estudio realizado por Álvarez y Lovera (2022). En tal sentido, resaltan zonas con una probabilidad de ocurrencias de anomalías mayores al 60 % en la parte central y SE del área de estudio, lo cual coincide con la Mina La Merced de Buenos Aires (Figura 7c). Además, estos resultados tienen una correlación significativa con la ley de 57.45 g/t Au obtenida en un balance metalúrgico realizado por Ichau (2019) en muestras provenientes de dicha mina.
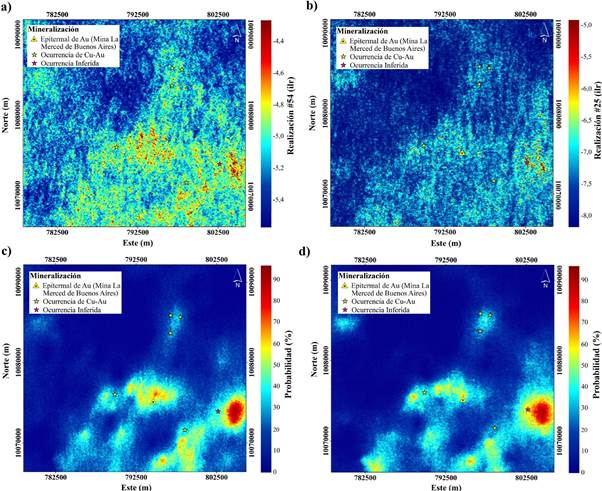
Figura 8 a) Mapa de realización óptima #54 para indicadores geoquímicos de Au-Ag. b) Mapa de realización óptima #25 de elementos perjudiciales. c) Mapa de probabilidad de ocurrencias anómalas de Au-Ag. d) Mapa de probabilidad de ocurrencias anómalas de elementos perjudiciales
Asimismo, en la Figura 7b se tienen los resultados de la realización #25 correspondiente a elementos perjudiciales en el proceso de recuperación por lixiviación, donde se evidencia valores por encima de -6.5 (ilr), lo que sugiere la presencia de zonas anómalas en la parte central y SE del plano geoquímico, no obstante, con la finalidad de interpretar zonas anómalas de mejor manera, se ha determinado la probabilidad por encima de -7.07 (ilr) en base a la clasificación realizada por Álvarez y Lovera (2022) para este grupo multielemental (Figura 7d). En ese sentido, se evidencia la presencia de elementos perjudiciales en el proceso de lixiviación sobre la Mina La Merced de Buenos Aires con una probabilidad mayor a 50 %, sin embargo, en el estudio realizado por Ichau (2019) no se ha tomado en cuenta estos elementos durante las pruebas para el balance metalúrgico antes mencionado, lo que probablemente afecte el porcentaje de recuperación en la planta de procesos a gran escala. En este contexto, se evidencia fuerte correlación entre los resultados de los planos multielementales, adicionalmente, tanto el grupo de indicadores geoquímicos y de elementos perjudiciales tiene un comportamiento similar lo que probablemente se debe a que muchos elementos que se clasifican como IG también actúan negativamente en los procesos físico-químicos de recuperación metalúrgica. Además, geoestructuralmente las anomalías responden al rumbo del sistema de fallas principal en dirección NE-SW y a la presencia de cuerpos intrusivos en zonas específicas del área de estudio; lo que a su vez ha permitido inferir una ocurrencia de mineralización al SE (Figura 7). Por otra parte, el método de SGS en esta investigación ha permitido ilustrar la variabilidad de la concentración de IG y elementos perjudiciales, considerando que, al calcular múltiples realizaciones para anomalías geoquímicas de la zona de estudio se puede evaluar escenarios posibles que reproduzcan adecuadamente las estadísticas (Anexo 2, 3) y variogramas (Figuras 7b y 7d) de cada grupo multielemental, demostrando la efectividad de la SGS. En consecuencia, se corrobora en este estudio que al aplicar Simulación Secuencial Gaussiana se tiene una representación no suavizada de la realidad, respetando la variabilidad espacial de las muestras originales. Además, tradicionalmente en los estudios geoquímicos se definen anomalías por medio del background, umbral y anomalías (baja, media y alta) a partir de los datos estimados y la suma de la desviación estándar (Álvarez & Lovera, 2022) lo que genera cierto grado de incertidumbre; por lo cual, en la presente investigación se ha optado por determinar la probabilidad en porcentaje de ocurrencias minerales al considerar un valor optimista por encima del umbral para los dos grupos multielementales, esto ha permitido una mejor interpretación de zonas anómalas (Figuras 7c y 7d), por lo tanto, esta metodología ofrece una mayor precisión por encima del 60 %, lo que es favorable en estudios exploratorios para definir de manera más precisa zonas para labores prospectivas a detalle o puntos de perforación. Este aspecto no se ha considerado en los trabajos desarrollados por Álvarez y Lovera (2022), Zheng et al. (2023), Zhou et al. (2020) y Zuo (2021), en consecuencia, esta investigación constituye un complemento fundamental para la exploración de minerales metálicos en el futuro, ya que al utilizar técnicas estocásticas se obtienen resultados más realistas. Asimismo, la integración de variables tal como la concentración de elementos perjudiciales en el proceso de lixiviación de Oro, ratifica la importancia del enfoque geometalúrgico desde la fase inicial de la minería propuesto por Álvarez y Lovera (2022), el cual debe ser parte de los diagramas de flujo en la planificación de labores prospectivas.
4. CONCLUSIONES
En los estudios de exploración minera, al elaborar el procesamiento de datos geoquímicos es conveniente tomar en cuenta su naturaleza composicional para convertirlos de un sistema cerrado a un sistema abierto por medio de transformaciones clr e ilr, las cuales permiten realizar un mejor análisis correlativo del conjunto de muestras al eliminar la problemática relacionada con valores atípicos, aprovechar toda la información disponible y evitar falsas correlaciones. Además, el potencial de estas transformaciones radica en hacer análisis multivariables independientemente de la existencia de relación de dependencia, lo que hace que sea factible aplicar el criterio del investigador, la experiencia y la realidad del fenómeno, tal como se evidenció en la presente investigación al conformar los dos grupos multielementales de IG y perjudiciales. Por ende, esto permite corroborar la efectividad del análisis composicional, aplicable desde la fase exploratoria de la minería para estudios geometalúrgicos. Los planos de indicadores geoquímicos para Oro y Plata y de elementos perjudiciales en el proceso de lixiviación determinados a partir de Simulación Secuencial Gaussiana, evidencian resultados más acordes con la realidad ya que reproducen de mejor manera las estadísticas y su variabilidad espacial, en ese sentido, reducen significativamente el grado de incertidumbre presente en otros métodos de estimación geoestadística. Igualmente, las anomalías obtenidas se correlacionan positivamente con información de la Mina La Merced de Buenos Aires, las cuales siguen a su vez un comportamiento estructural similar al sistema de fallas principal, lo que también tiene relación con la presencia de cuerpos intrusivos. Asimismo, al considerar la evaluación del porcentaje de probabilidad de ocurrencias minerales de Au-Ag y de elementos perjudiciales en el proceso de lixiviación, no solo facilita la interpretación de zonas anómalas, sino también garantiza áreas más susceptibles para labores de exploración a detalle y/o de perforación.
Adicionalmente, cabe notar que es indispensable la integración del enfoque geometalúrgico desde los estudios prospectivos, exploratorios y en las subsiguientes etapas en la cadena de valor de la minería; esto permitirá tener un mayor grado de confianza especialmente en distritos con potencial minero donde se dispone de información geometalúrgica y, también, reducir el riesgo asociado a las inversiones en las fases iniciales de un proyecto, mejorando el aprovechamiento de los recursos metalíferos.