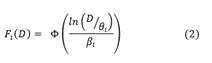1. INTRODUCCIÓN
El desempeño sísmico de las estructuras puede ser afectado por la presencia de irregularidades en la configuración estructural. En pasados terremotos (Japón, 1995; Chile, 2010; Ecuador, 2016), se ha evidenciado la incidencia de las irregularidades estructurales en el comportamiento sísmico de las estructuras (Aguilar et al., 2016; EERI, 2016; FEMA P-2012, 2018; Páez et al., 2017; Sritharan et al., 2014; Tena, 2010). El FEMA P-2012 (2018) menciona que las irregularidades estructurales pueden ser abordadas de tres maneras: removiendo las irregularidades del diseño estructural, tomando en cuenta las irregularidades por medio de un procedimiento analítico o tratando las irregularidades desde un enfoque de diseño. En el caso de este estudio, las irregularidades son abordadas por medio del procedimiento analítico.
Una de las irregularidades estructurales en planta es la irregularidad torsional (IT), la cual se encuentra definida como, la relación entre la deriva máxima de piso ( ∆ max ) incluyendo la torsión accidental y la deriva promedio ( ∆ 𝑝𝑟𝑜𝑚 ) de los extremos del mismo entrepiso. Si la relación entre deriva máxima de piso y deriva promedio es mayor o igual a 1,2 se considera que la estructura tiene irregularidad torsional (ver Ecuación (1)) y si la relación entre deriva máxima de piso y deriva promedio es mayor o igual a 1,4 se considera que la estructura tiene irregularidad torsional extrema (ASCE, 2016).
Los códigos de diseño cumplen la función de dar recomendaciones prescriptivas para procurar un buen comportamiento estructural ante solicitaciones externas como son los terremotos. Varias normativas (ASCE, 2016; NORMA E030, 2020; NSR-10, 2012) presentan límites y condiciones para el nivel de IT que pueden tener las estructuras dependiendo de la categoría de diseño sísmico o categoría de la edificación. Estas recomendaciones y restricciones se basan en: el tipo de análisis numérico al que debe ser sometida la estructura, aumento en las solicitaciones de los elementos estructurales por medio del factor de amplificación de la torsión accidental o coeficientes de irregularidad que afecta al porcentaje de corte basal, y limitaciones en el uso de estructuras con niveles de IT mayores a 1,4. La Norma Ecuatoriana de la Construcción (NEC-SE-DS, 2015) en su capítulo de diseño sísmico ubica a la irregularidad torsional dentro del grupo de irregularidades horizontales. Debido a que la NEC-SE no tiene límites ni restricciones adicionales cuando las estructuras tienen una relación de irregularidad torsional extrema, se plantea evaluar el desempeño sísmico en función de este parámetro.
Este estudio busca evaluar la variabilidad del desempeño sísmico en función del nivel de irregularidad torsional. Por lo que se plantea el diseño y evaluación de tres arquetipos, cada uno con un nivel de IT diferente (IT 1.0, IT 1.2 e IT 1.4), de 16 pisos de altura conformados por un sistema dual de hormigón armado (pórticos y muros especiales). Se desarrollan modelos no lineales con elementos tipo fibra con una formulación basada en fuerzas (infrmFB) para las secciones de muros estructurales y columnas, mientras que los elementos vigas son representados con elementos de plasticidad concentrada (infrmFBPH). Los análisis no lineales son evaluados ante once registros sísmicos seleccionados de la base de datos PEER. Para elaborar las curvas de fragilidad se toman como parámetro de demanda ingenieril (EDP) las derivas de piso y deformaciones unitarias. Por último, se desarrollan curvas de fragilidad para los niveles de desempeño de ocupación inmediata (OI), seguridad de vida (SV) y prevención de colapso (PC), y se obtienen los coeficientes de margen (MR) de cada uno de los niveles de desempeño. Los coeficientes de margen representan la razón entre la intensidad mediana de los niveles de desempeño y la aceleración espectral del diseño elástico.
Finalmente, se cuantificó la probabilidad de alcanzar el nivel de desempeño de prevención de colapso ante el sismo máximo considerable para los modelos IT 1.0, IT 1.2 e IT 1.4, siendo esta el 3,54 %, 18,29 % y 31,60 %, respectivamente. Por lo que se concluye que a mayor nivel de irregularidad torsional mayor es la probabilidad de alcanzar el nivel de desempeño de prevención de colapso.
Para investigaciones futuras, se recomienda evaluar la incidencia en el desempeño sísmico en las estructuras con IT 1,4 cuando presentan valores de derivas de piso totales menores al 50 % de la deriva máxima recomendada por el código (NORMA E030, 2020) o se amplifica la fuerza sísmica en las combinaciones de carga por un factor igual a 1,3 para el diseño de los elementos estructurales (ASCE, 2016).
2. DEFINICIÓN, ANÁLISIS Y DISEÑO DE LOS ARQUETIPOS
2.1 Definición de arquetipos
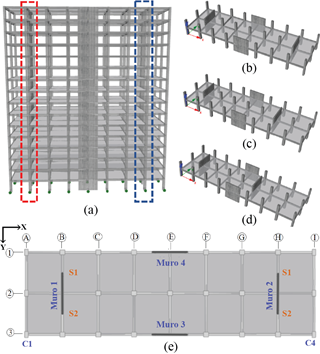
Para medir la variabilidad del desempeño sísmico, se plantean tres arquetipos con diferentes niveles de irregularidad torsional (IT 1.0, IT 1.2 e IT 1.4). En la Figura 1, se presenta el modelo base, el cual consta de 16 pisos y un sistema estructural de muros y pórticos especiales de hormigón armado. Los tres arquetipos tienen similares dimensiones en planta (ancho: 12,0 m y largo: 40,0 m) y un entrepiso constante de 2,9 m (altura total del edificio: 46,4 m). La separación perpendicular entre los pórticos direccionados en el sentido X y Y es 6,0 m y 5,0 m, respectivamente. Como se observa en la Figura 1(a), el muro señalado con un cuadro color azul (muros en sentido Y) se va a mover de posición de derecha a izquierda, y así imponer diferentes niveles de IT. Al muro señalado con un cuadro rojo se le denomina Muro 1 y al muro señalado con un cuadro azul se le denomina Muro 2. Cabe mencionar que se mantienen las mismas dimensiones de los elementos estructurales (vigas, columnas y muros) en los tres modelos.
La Figura 1(b) presenta el esquema del modelo con un nivel de irregularidad torsional igual a 1,0 (Modelo IT 1.0). Las Figura 1(c) y Figura 1(d) presentan la configuración estructural de los modelos con irregularidad torsional mayores a 1,2 (Modelo IT 1.2) y 1,4 (Modelo IT 1.4), respectivamente. La Figura 1(e) presenta un esquema en planta de la ubicación de los muros estructurales (Muro 1 y Muro 2), ubicación de las columnas y esquinas de losa (C1 y C4) que sirven de referencia para cuantificar la relación de irregularidad torsional, y los sectores S1 y S2 que son las zonas donde se evaluarán las deformaciones unitarias a compresión y tensión debido a las solicitaciones sísmicas.
Se comprueba que el modelo IT 1.0 tiene niveles de IT iguales a la unidad en ambos sentidos (X y Y), el modelo IT 1.2 presenta niveles de IT de 1,0 (sentido X) y 1,37 (sentido Y), y el modelo IT 1.4 tiene niveles de IT de 1,0 (sentido X) y 1,6 (sentido Y). Se observa que la relación de irregularidad torsional se mantiene constante (IT = 1,0) en el sentido X, mientras que en el sentido Y se presenta 3 diferentes niveles de irregularidad torsional debido al cambio de ubicación del Muro 2.
2.2 Análisis y diseño de los arquetipos
A continuación, se presenta el procedimiento de diseño de los tres arquetipos seleccionados. El espectro elástico de diseño fue determinado con los coeficientes y parámetros que estipula la NEC (2015). Los tres arquetipos se encuentran ubicados en la ciudad de Quito sobre un suelo tipo D. En la Figura 2, se grafica el espectro elástico de diseño (DBE; 10 % de probabilidad de excedencia en 50 años), el espectro del sismo máximo considerable (MCE; 2 % de probabilidad de excedencia en 50 años) y el espectro del sismo de servicio (SE; 50 % de probabilidad de excedencia en 50 años). Los espectros MCE y SE fueron determinados de manera aproximada al multiplicar el espectro DBE por 1,5 y 0,5, respectivamente (Cagua, 2022).
El factor de importancia es 1,0, y el tipo de uso es residencial para todos los arquetipos. El valor de la sobrecarga es 29,24 MPa y 19,61 MPa para carga muerta y viva, respectivamente. El valor del esfuerzo de compresión del concreto es 27,45 MPa y el esfuerzo de fluencia del acero es 411,88 MPa. El valor del módulo de elasticidad del hormigón es igual a 24 778,59 MPa (NEC-SE-HM, 2015). Se usaron las combinaciones de carga tal como se especifica en la NEC-SE-CG (2015).
Los elementos estructurales vigas, columnas, muros y losas fueron agrietados por los siguientes coeficientes: 0,5, 0,8, 0,6 y 0,35, respectivamente (NEC-SE-DS, 2015). El factor de reducción de resistencia sísmica (R) es 7. Todos los arquetipos fueron diseñados con un porcentaje de corte basal igual a 9,3 % (V= 6 728,64 kN). Se verifica que los muros estructurales en ambos sentidos absorben más del 75 % del corte basal. Los muros en sentido X, al no tener un cambio en la irregularidad torsional, mantienen constante el porcentaje de corte basal absorbido por los muros (75,6 %). En el sentido Y, el porcentaje de corte absorbido por los muros estructurales varía, ya que en este sentido los niveles de irregularidad torsional también varían (IT 1.0: 77 %, IT 1.2: 76,6 % e IT 1.4: 74,6 %). Todos los arquetipos cumplen con el límite de deriva permisible del 2,0 %.
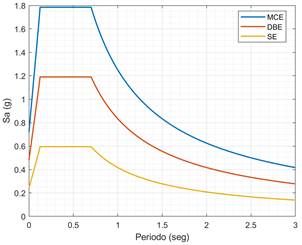
Figura 2 Espectros elásticos según NEC-SE-DS. Sismo máximo considerado (MCE), sismo de diseño (DBE) y sismo de servicio (SE)
El diseño estructural fue elaborado con las recomendaciones del ACI 318-19 (2019) y NEC-SE- HM (2015). Los refuerzos longitudinales de columnas fueron obtenidos ante las solicitaciones de flexo - compresión, por lo que fue necesario revisar los diagramas de interacción (axial - momento) para verificar su cumplimiento. El diseño a corte de las columnas se lo realizó con los criterios de diseño por capacidad en donde se involucran los momentos máximos probables de las columnas para poder obtener el corte de diseño (ACI 318-19, 18.7.6.1.1). Los espaciamientos de estribos y chequeo de confinamiento en columnas fueron revisados con ACI 318-19,18.7.5. El diseño a corte de vigas se lo realizó con los criterios de diseño por capacidad en donde se involucran los momentos máximos probables en vigas para poder obtener el corte de diseño (ACI 318-19, 18.6.5.1). Los espaciamientos de estribos se especificaron acorde a ACI 318-19,18.6.4.
Los aceros longitudinales del alma y cabezales de los muros estructurales fueron obtenidos con el diseño a flexo - compresión. La longitud de los elementos de borde se obtuvo con las expresiones mencionadas en el ACI 318-19,18.10.6.2 y NEC-SE-HM,6.1.5.C, las cuales involucran el cálculo del eje neutro (c) al presentarse una deformación unitaria igual a 0,003 en el extremo del muro que se encuentra a compresión. Los elementos de borde o cabezales cumplen con las exigencias de confinamiento mencionadas en ACI 318-19,18.7.5. Para el diseño a corte de los muros estructurales se consideró el factor de sobre-resistencia ( Ω 𝑣 ) y el factor de amplificación dinámica de corte ( 𝜔 𝑣 ). Al determinar cada uno de los coeficientes y tomando en cuenta el límite establecido en el ACI 318-19,18.10.3.1, las solicitaciones a corte en todos los muros fueron amplificados por un factor igual a 3. Finalmente, se verificó el chequeo de la conexión viga-columna especificado en el ACI 318-19,18.7.3. Esta recomendación exige que la sumatoria de momentos nominales de las columnas deben ser 1,2 veces mayor a la sumatoria de los momentos nominales de vigas.
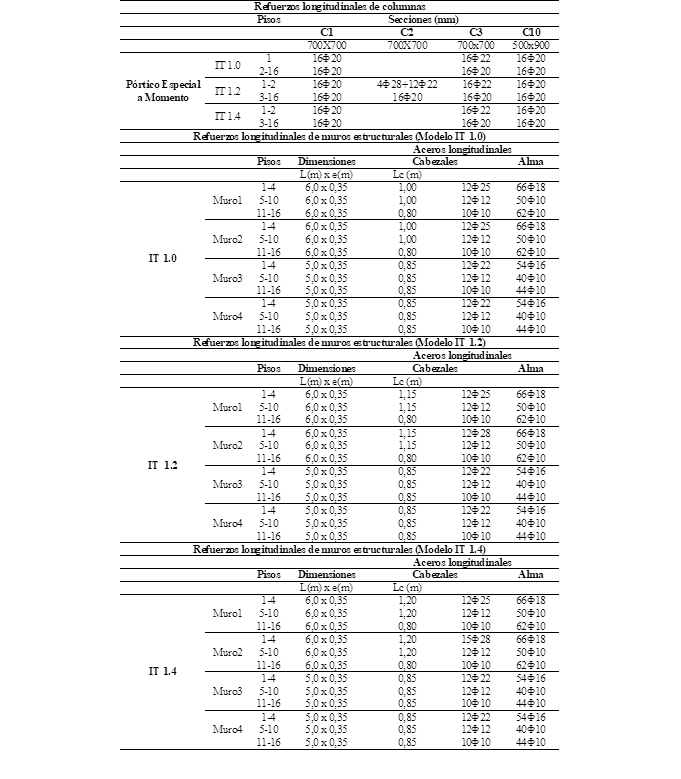
En la Tabla 1 (Ver Anexo), se presentan las secciones finales de columnas y muros estructurales de los tres arquetipos y sus respectivos refuerzos longitudinales. Los pórticos exteriores (Eje A y Eje I) de los tres arquetipos tienen columnas tipo C10. Las columnas de los ejes B y H tienen secciones tipo C3 en el modelo IT 1.0. Las columnas del eje B tienen secciones tipo C2 y las columnas del eje G tienen secciones tipo C3 en el modelo IT 1.2. Las columnas del eje B y F tienen secciones tipo C3 en el modelo IT 1.4. El resto de las columnas tienen una sección tipo C1. En todos los arquetipos, los muros estructurales direccionados en el eje Y (Muro 1 y Muro 2) tienen una longitud (L) de 6,0 m y un espesor (e) de 0,35 m. Los muros direccionados en el eje X tienen una longitud de 5,0 m y un espesor de 0,35 m. las longitudes de los cabezales (Lc) o elementos de borde varían entre 1,20 m y 0,85 m, dependiendo de la ubicación en altura del muro. Los aceros horizontales de los Muro 1, Muro 3 y Muro 4, en los cuatro primeros pisos de todos los arquetipos, son 2Ф16mm @ 100 mm. El refuerzo horizontal del Muro 2 del modelo IT 1.0 es 2Ф16mm @ 100 mm, mientras que el Muro 2 para los modelos IT 1.2 e IT 1.4 se refuerza con 2Ф18mm @ 100 mm. Las vigas tienen una dimensión de 300 mm x 500 mm en todos los entrepisos de todos los arquetipos.
3. CALIBRACIÓN DEL ELEMENTO TIPO FIBRA PARA EL MODELO DE MUROS ESTRUCTURALES
La calibración consiste en estimar la respuesta (global o local) de un elemento estructural mediante el uso de un modelo matemático de elementos finitos y luego comparar los resultados analíticos con resultados experimentales obtenidos en ensayos de laboratorio. Mediante este procedimiento de calibración es posible establecer parámetros para la generación de los modelos constitutivos de los materiales (acero y concreto) y las características que deben tener los elementos modelados (número de fibras, puntos de integración, número de elementos y convergencia). Actualmente para calibrar el modelo matemático de un muro de corte es posible usar dos tipos de modelos: macroscópicos y microscópicos (Almeida et al., 2014; Fischinger et al., 2019; Kolozvari et al., 2018).
Los modelos macroscópicos o macroelementos tienen la característica de tener una mayor robustez en sus formulaciones y los parámetros de ingreso. A pesar de esta característica, los macroelementos han logrado capturar las respuestas globales y locales de elementos estructurales con cierto grado de exactitud. Uno de los beneficios de tener formulaciones más robustas es el menor tiempo de ejecución para realizar las evaluaciones y un menor costo computacional. Los macroelementos están definidos por fibras, resortes o armaduras. Multiple Vertical Line Element Model (MVLEM), Shear-Flexure Interaction Multiple Vertical Line (SFI-MVLEM) y modelos de fibras de plasticidad distribuida son algunos de los macro modelos existentes en la actualidad.
El modelo MVLEM tiene la característica de que captura la respuesta global del elemento tiendo en cuenta la interacción axial - flexión, pero desacoplando la acción del cortante. El modelo SFI-MVLEM se caracteriza por tener una interacción corte - axial - flexión. El modelo SFI-MVLEM al tener este tipo de interacción se lo conoce como un modelo acoplado y tiene la posibilidad de lograr capturar las deformaciones debido al corte (Kolozvari et al., 2015). Los modelos MVLEM y SFI-MVLEM se encuentran en la plataforma Opensees (McKenna et al., 2000).
Los modelos de plasticidad distribuida (elemento tipo fibra) tienen varias secciones transversales (secciones Gauss), las cuales se encuentran conformadas por n número de fibras. Cada fibra tiene una relación uniaxial esfuerzo - deformación que caracteriza el modelo constitutivo del material (concreto o acero). La respuesta histerética del elemento queda implícitamente representada al incorporar los modelos constitutivos de los materiales en cada una de las fibras (Seismosoft, 2022). Este tipo de elemento logra capturar la interacción axial - momento. El cortante en este elemento se encuentra desacoplado. Adicionalmente, se puede usar dos tipos de formulaciones: formulación basada en fuerzas (FB) y formulación basada en desplazamientos (DB). Gharakhanloo (2014) menciona que una de las principales diferencias entre los elementos con formulación DB y FB es que los elementos con formulación DB requiere un mayor número de elementos para modelar un mismo miembro y logar obtener respuestas similares a los elementos con formulación FB. Esta diferencia hace que se requiera un mayor tiempo de análisis y uso de memoria del ordenador en el caso de usar elementos con formulación DB. Por este motivo, los elementos estructurales (columnas y muros de corte) fueron modelados con elementos tipo fibra con formulación basada en fuerzas.
Los micro modelos son modelos desarrollados por elementos finitos más refinados. Estos tipos de modelos logran captura de mejor manera las respuestas estructurales locales y globales obtenidas en ensayos de laboratorio. En los micro modelos es posible considerar las deformaciones por corte, las cuales tienen una gran contribución en el comportamiento de muros bajos. Debido al refinamiento del modelo matemático los micro modelos pueden capturar respuestas más detalladas tales como el aplastamiento el concreto en muros esbeltos ante grandes cargas axiales con elementos de borde con poco confinamiento o la diagonal a tensión en muros donde predomina el corte (Fischinger et al., 2019).
Los muros estructurales se clasifican según su relación de aspecto (altura del muro/longitud del muro o h/lw), ya que de esta relación depende el comportamiento del muro estructural. Los muros estructurales esbeltos son los que tienen una relación de aspecto mayor a 3 (h/lw >3) y su comportamiento es gobernado por la flexión. En los muros esbeltos la mayoría de las deformaciones es ocasionada por la flexión. Los muros estructurales con estas características pueden ser analizados con los modelos MVLEM o elementos tipo fibra, ya que las deformaciones que predominan son las de flexión. Los muros estructurales bajos son los que tienen una relación de aspecto menor a 1 (h/lw <1) y su comportamiento es gobernado por el corte. En el caso de este tipo de muros las deformaciones por cortante son representativas por lo que las deformaciones totales del muro son limitadas por las deformaciones a corte. Este tipo de muros estructurales pueden ser analizados por medio del modelo SFI-MVLEM, ya que este modelo matemático incorpora la interacción corte - axial - flexión. Dado que los muros estructurales usados en los tres arquetipos tienen una relación de aspecto mayor a 3, se analiza el muro RW2 presentado en el estudio de Thomsen y Wallace (2004) para la calibración del modelo matemático.
3.1 Ensayo experimental en muros
El muro RW2 se encuentra en el estudio y ensayo experimental realizado por Thomsen y Wallace (2004). El muro RW2 tiene una relación de aspecto igual a 3 por lo que el comportamiento predominante será la flexión. Las dimensiones del muro RW2 son: 1 219 mm, 102 mm y 3 658 mm (longitud, espesor y altura, respectivamente). El espécimen fue sometido a desplazamientos laterales cíclicos por medio de un actuador hidráulico horizontal. Los patrones de desplazamientos laterales pueden ser revisados en el estudio realizado por Orakcal y Wallace (2006). Adicionalmente, se aplicó una carga axial (P= 0,007 Ag f´c, donde Ag es el área bruta de la sección transversal y f´c es el esfuerzo a compresión del concreto) en la parte superior del muro, la cual fue constante en todo el ensayo. El esfuerzo de compresión del concreto al momento del ensayo presentó un rango entre 28,7 MPa a 58,4 MPa y un esfuerzo de compresión promedio de 34 MPa. El refuerzo longitudinal del muro tenía varillas No. 2 (32,17 mm2) para el alma del muro y No. 3 (70,88 mm2) para el sector de los cabezales. El refuerzo transversal del alma del muro tenía un diámetro de No. 2 (32,17 mm2) y 3/16 in (17,81 mm2) para el sector de los cabezales.
3.2 Modelo matemático del muro experimental
El muro estructural RW2 se modeló en SeismoStruct con elementos inelásticos de pórtico con formulación basada en fuerzas (infrmFB). El elemento infrmFB está conformado por 5 secciones de integración y 500 fibras en sus secciones transversales. La base del muro se encuentra empotrada y en la parte superior de muro se aplica una carga axial constante igual a 0,007 Ag f´c.
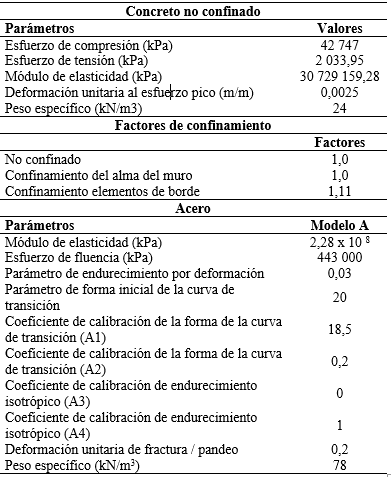
Para representar el concreto se usó el modelo “con_ma”, el cual usa las reglas constitutivas propuesta por Mander et al. (1988) y las leyes del comportamiento no lineal cíclico propuestas por Martinez-Rueda y Elnashai (1997). Para los valores de esfuerzo de compresión, esfuerzo de tensión y módulo de elasticidad se tomó como referencia los parámetros recomendados por Orakcal y Wallace (2006) (Ver Anexo, Tabla 2).
El acero de refuerzo fue representado por el modelo de acero “stl_mp”, el cual usa la relación esfuerzo - deformación propuesta por Menegotto-Pinto (1973) y las leyes de endurecimiento isotrópico propuestas por Filippou et al. (1983). Para el valor del esfuerzo de fluencia se tomó como referencia los valores presentados en Echeverría-Landeta et al. (2022) y Orakcal y Wallace (2006); el parámetro de endurecimiento por deformación usado fue 0,03 al tomar como referencia el estudio de Gallardo et al. (2021); el parámetro de forma inicial de la curva de transición (R) es 20 según Echeverría-Landeta et al. (2022) y los valores por defecto que recomienda SeismoStruct (2022); los coeficientes de calibración A1, A2, A3 y A4 fueron tomados de acuerdo a las recomendaciones por defecto que proporciona SeismoStruct (2022) (Ver Anexo, Tabla 2).
3.3 Comparación de los resultados del modelo analítico y modelo experimental
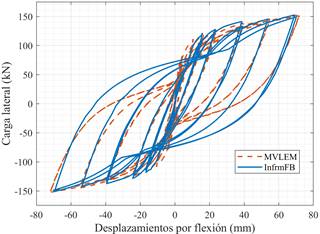
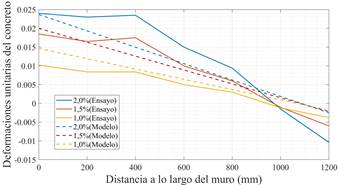
En el estudio de Orakcal y Wallace (2006), se detallan los valores de los desplazamientos en el tope del muro durante el ensayo experimental. Adicionalmente, menciona que existen tres tipos de desplazamientos medidos: a) desplazamiento superior aplicado, b) desplazamiento superior con la contribución del movimiento del pedestal restado y c) desplazamiento superior con el movimiento del pedestal y deformaciones de corte restadas. Debido a que el macro modelo usado solo contempla la interacción axial - momento, es importante comparar las respuestas de desplazamiento superior, pero por flexión, tal como lo detalla Orakcal y Wallace (2006). La respuesta del modelo numérico se obtuvo con la ayuda del modelo MVLEM (multiple-vertical-line-element model) que se puede encontrar en la plataforma de OpenSees. Debido a que la respuesta numérica obtenida con el modelo MVLEM tiene una buena aproximación a la respuesta experimental (Orakcal & Wallace, 2006), se procedió a comprar la respuesta analítica obtenida en Opensees con la respuesta analítica con el modelo infrmFB (ver Figura 3). En la Figura 4 se compara las deformaciones unitarias obtenidas en el ensayo experimental (Orakcal & Wallace, 2006; Thomsen & Wallace, 2004) y las deformaciones unitarias obtenidas con el modelo infrmFB.
La Figura 3 muestra como el modelo infrmFB logra capturar valores similares de desplazamiento máximo (70,12 mm) y carga lateral máxima (149 kN) con respecto a los resultados obtenidos con el modelo MVLEM. A pesar de que el modelo infrmFB no logra capturar la disminución de la pendiente de la curva histerética mientras aumentan los ciclos del ensayo, los valores de deformaciones unitarias a tensión en el extremo del muro son relativamente similares con respecto a los ensayos experimentales, especialmente cuando los valores de derivas de piso se encuentran entre 1,5 % y 2,0 % (ver Figura 4).
4. MODELO NO LINEAL DE LOS ARQUETIPOS
En función de los parámetros encontrados en la calibración del modelo matemático se procedió a elaborar los modelos no lineales de los tres arquetipos. El valor de esfuerzo a compresión del concreto es 27,45 MPa y el esfuerzo de fluencia del acero es 411,88 MPa. Para el modelo de los muros y columnas se usó elementos inelásticos de pórtico con formulación basada en fuerzas (infrmFB) y para las vigas se usó elementos inelásticos de pórtico de rótula plástica con formulación basada en fuerzas (infrmFBPH). El número de fibras en las secciones transversales usadas son: 131, 400 y 150 para columnas, muros y vigas, respectivamente. Se consideraron tres tipos de materiales: hormigón no confinado (con_ma), hormigón confinado y acero de refuerzo (stl_mp).
5. NIVELES DE DESEMPEÑO SÍSMICO
En el presente estudio, se usan los valores de derivas de piso y deformaciones unitarias para poder definir los diferentes niveles de desempeño estructural y estados límite. Adicionalmente, se buscará encontrar una relación entre derivas de piso y deformaciones unitarias para especificar varios niveles de desempeño estructural, y poder comprar ambas metodologías de evaluación por medio de la elaboración de curvas de fragilidad con ambas medidas de daño.
Los niveles de desempeño estructural cuando se toma como parámetro las derivas de piso son: ocupación inmediata (OI; 0,5 %), seguridad de vida (SV; 1%) y prevención de colapso (PC; 2 %), tal como lo detalla FEMA 356 (2000). Debido a que los valores de derivas indicados en el FEMA 356 pretenden ser descripciones cualitativas del comportamiento aproximado de las estructuras que cumplen dichos niveles; y no reemplazan la evaluación local de los límites de deformación de los componentes estructurales (FEMA 356, 2000). También se propone la evaluación del desempeño sísmico por medio de la medición de deformaciones unitarias en los elementos críticos que forman parte del sistema resistente a carga lateral.
Al tomar como parámetro de evaluación las deformaciones unitarias, los estados límite evaluados son: fluencia, servicio y colapso. El valor de deformación unitaria para el estado límite de fluencia es 𝜀 𝑠 = 𝑓 𝑦 / 𝐸 𝑠 y 𝜀 𝑐 =0,002 (Priestley & Kowalsky, 2000); donde 𝜀 𝑠 es la deformación unitaria a tensión del acero de refuerzo, 𝑓 𝑦 es el esfuerzo de fluencia, 𝐸 𝑠 corresponde al módulo de elasticidad del acero de refuerzo y 𝜀 𝑐 es la deformación unitaria a compresión del concreto. Los valores de deformación unitaria para el estado límite de servicio son: 𝜀 𝑠 =0,015 y 𝜀 𝑐 =0,004 para el acero de refuerzo a tensión y el concreto a compresión, respectivamente (Priestley & Kowalsky, 2000). Para definir el colapso se tomó en cuenta los siguientes criterios: (1) inestabilidad lateral dinámica, dicha inestabilidad se produce cuando las cargas verticales generan un efecto desestabilizador (efecto P - Δ) que supera a la resistencia lateral de la estructura, por lo que, la respuesta de desplazamiento aumenta significativamente ante variaciones de intensidades pequeñas (Araya-letelier et al., 2019; Cando, 2020), (2) falla ante cargas axiales, la falla ante cargas axiales se relaciona con el valor de la deriva lateral que puede llegar a alcanzar el edificio, para edificios de mediana altura se establece un valor de deriva límite igual al 5% según las recomendaciones de Gogus y Wallace (2015) y (3) el 50 % de los muros estructurales que conforman el sistema resistente a carga lateral presentan cualquiera de las siguientes fallas: pandeo del acero, fractura del acero, aplastamiento del hormigón (Cando, 2020) e inestabilidad de pandeo fuera del plano (Haro et al., 2019).
La fractura o pandeo del acero de refuerzo se produce cuando la deformación unitaria axial (tensión o compresión) del refuerzo alcanza un valor de 0,05 (ACI-318, 2019; Cando et al., 2020; Dabaghi et al., 2019; Gogus & Wallace, 2015). El aplastamiento en el concreto se produce cuando la deformación unitaria axial del concreto (compresión) supera el límite de aplastamiento según la curva esfuerzo - deformación. El punto límite de aplastamiento (deformación unitaria después de alcanzar el esfuerzo pico del concreto confiando) se produce cuando el concreto alcanza un valor residual de esfuerzo igual al 20 % del esfuerzo pico del concreto confinado (Dabaghi et al., 2019; Gogus & Wallace, 2015).
Haro, Kowalsky & Chai (2019), relacionan las deformaciones debido a cargas en el plano con la inestabilidad de pandeo fuero del plano del muro estructural. En el presente estudio, los valores límite de deformación unitaria a tensión para evitar la inestabilidad de pandeo fuera del plano ( 𝜀 𝑠𝑚 ) en el Muro 2 son: 0,056, 0,054 y 0,051 para los modelos IT 1.0, IT 1.2 e IT 1.4, respectivamente. Los valores de 𝜀 𝑠𝑚 fueron calculados con las expresiones detalladas en los estudios de Haro, Kowalsky & Chai (2019) y Sarango, Haro, Acuña & Caiza (2021).
6. SELECCIÓN DE REGISTROS SÍSMICOS
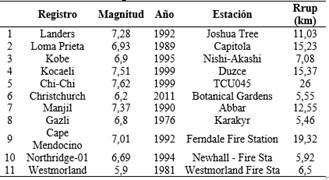
Los registros sísmicos fueron obtenidos de la base de datos del PEER Ground Motion Database (PEER, 2002), plataforma web que almacena la información de cientos de eventos sísmicos. Se utilizaron los criterios usados en el estudio probabilista de amenaza sísmica de Cagua (2022) para definir las características de los registros sísmicos seleccionados. Los criterios utilizados para la selección de registros sísmicos son los siguientes: magnitudes mayores a M 5,9, aceleraciones del suelo (PGA) mayores a 0,25 (g), suelo tipo D (Vs > 200m/s) y distancia Rrup > 5 (km).
En la Tabla 3 (Ver Anexo), se presenta la lista de los 11 registros seleccionados. Debido a que los análisis dinámicos incrementales tienen una demanda computacional alta, en tiempos de ejecución y memoria computacional, dada la gran cantidad de análisis no lineales necesarios para crear las curvas IDA, se realizó el procedimiento de Intensidad de Arias con la finalidad de disminuir el tiempo de los registros sísmicos. Se tomó dos tiempos representativos para acortar el registro sísmico. El tiempo inicial corresponde al tiempo en el que la energía del terremoto alcanza un 5 %, y el tiempo final, corresponde al tiempo en el que la energía del terremoto alcanza un 95 %.
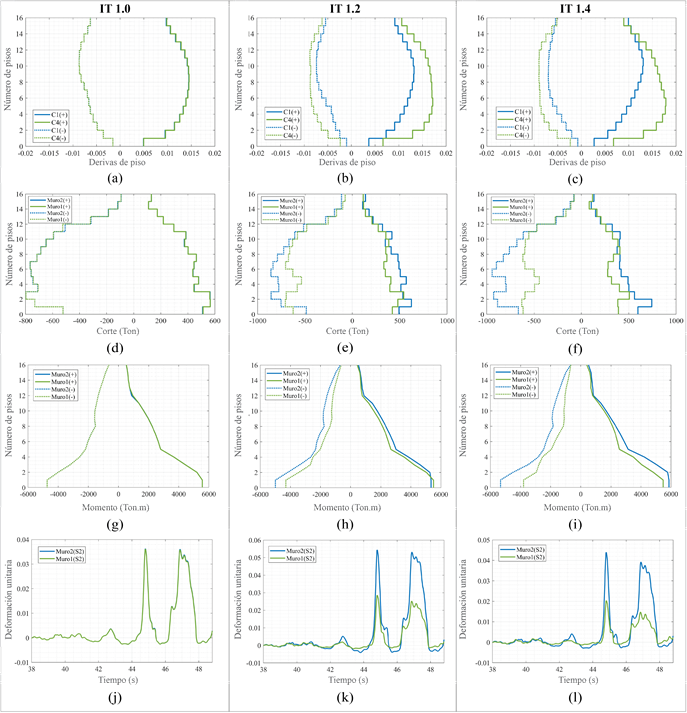
Figura 5 Respuestas globales y locales de los tres arquetipos ante el registro sísmico de Chi-Chi (Sa(T1,5%) = 0.6g): (a) Derivas de piso (IT 1.0), (b) Derivas de piso (IT 1.2), (c) Derivas de piso (IT 1.4), (d) Distribución de corte (IT 1.0), (e) Distribución de corte (IT 1.2), (f) Distribución de corte (IT 1.4), (g)
Distribución de momento (IT 1.0), (h) Distribución de momento (IT 1.2), (i) Distribución de momento (IT 1.4), (j) Distribución de deformaciones unitarias (IT 1.0), (k) Distribución de deformaciones unitarias (IT 1.2), y (l) Distribución de deformaciones unitarias (IT 1.4)
7. RESPUESTAS GLOBALES Y LOCALES DEL ANÁLISIS NO LINEAL
Se presentan los resultados del análisis no lineal (tiempo - historia) de los tres arquetipos tomando como amenaza el registro sísmico de Chi-Chi. El registro sísmico se encuentra escalado a un valor de Sa (T1,5%) igual a 0,6 (g). La Figura 5 presenta una comparación de las solicitaciones globales (derivas de piso) y locales (corte, momento, deformaciones unitarias) de cada uno de los arquetipos.
En la Figura 5(a), se puede observar que los valores de derivas de piso del modelo IT 1.0 son similares en ambas esquinas. En la Figura 5(b) y Figura 5(c), se puede verificar que mientras mayor es el nivel de irregularidad torsional mayor es la diferencia relativa de deriva de piso entre C1 y C4. Al comparar las derivas de piso de la esquina C4 entre los tres arquetipos, se puede observar que el modelo IT 1.4 es el modelo que mayor deriva de piso genera, a pesar de que los tres modelos fueron analizados con la misma amenaza. Las derivas de piso (piso 1- 6) del modelo IT 1.4 y Modelo IT1.2 son 1,38 y 1,35 veces mayores que las derivas de piso del Modelo IT 1.0, respectivamente. La Figura 5(d) muestra la distribución del corte, en ambos sentidos, del Muro 1 y Muro 2 del modelo IT 1.0; se puede verificar que se mantiene una relación de igualdad de cortantes entre ambos muros, a lo largo de toda la altura, al tener un modelo con una relación de IT cercana a la unidad.
En la Figura 5(e) y Figura 5(f), se detalla la distribución del corte del Muro 1 y Muro 2 de los modelos con IT 1.2 e IT 1.4, respectivamente; se puede comprobar que mientras mayor es el nivel de irregularidad torsional mayor es la diferencia de cortantes entre muros. Además, el Muro 2 aumenta su nivel de solicitación con respecto al Muro 1 (el Muro 1 disminuye su solicitación) mientras aumenta el nivel de irregularidad torsional. El Muro 2 (Piso 6) absorbe 1,89 y 1,37 veces más cortante que el Muro 1 en el modelo con IT 1.4 y IT 1.2, respectivamente. Al comparar la distribución de cortantes entre los tres arquetipos se verifica que el modelo IT 1.4 tiene un perfil de cortantes con mayores solicitaciones que los modelos IT1.0 e IT 1.2. En la Figura 5(g), se puede verificar que el porcentaje de momento absorbido por el Muro 1 y Muro 2 es igual, a lo largo de toda la altura del edificio, cuando el nivel de irregularidad es 1.0. La Figura 5(h) y Figura 5(i) muestran la variación de momento absorbido por el Muro 1 y Muro 2 cuando el nivel de la IT es 1.2 y 1.4. Se comprueba que el Muro 2 absorbe 1,74 veces más momento que el Muro 1 en el Piso 9 y 1,52 veces más momento que el Muro 1 en el Piso 2, cuando el nivel de irregularidad es IT 1.4. Se verifica que a mayor nivel de irregularidad torsional mayor es el valor de momento absorbido por el Muro 2, mientras disminuye el valor del momento en el Muro 1. Prácticamente en toda la altura del muro existe una variación de momentos dependiendo del nivel de irregularidad torsional, siendo los pisos altos los que mayor variación presentan.
En la Figura 5(j), Figura 5(k) y Figura 5(l), se presentan la distribución de las deformaciones unitarias en los sectores de evaluación S1 y S2 de los diferentes muros estructurales. Los sectores S1 y S2 están conformados por varias fibras de concreto no confinado, concreto confinado y aceros longitudinales.
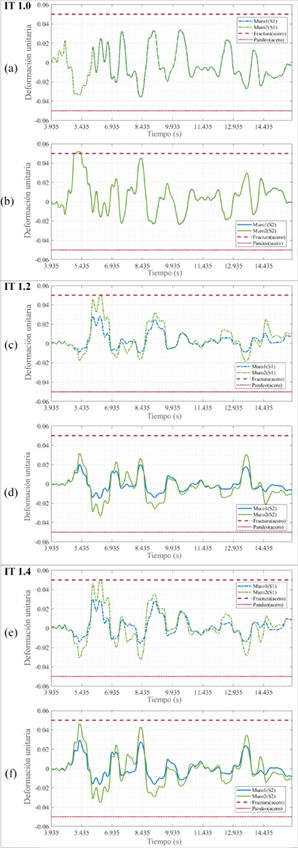
Figura 6 Registros de deformaciones unitarias (Registro de Loma Prieta): (a), (b) modelo IT 1.0, (c), (d) modelo IT 1.2 y (e), (f) modelo IT 1.4
Nuevamente se puede verificar que al tener una relación de IT 1.0 las solicitaciones locales (deformaciones unitarias) se mantienen con la misma distribución en los cuatro sectores de ambos muros estructurales. Las Figura 5(k) y Figura 5(l) muestran cómo se disminuye los valores de deformaciones unitarias en el sector S2 del Muro 1 mientras aumenta el nivel de irregularidad torsional.
8. EVALUACIÓN DE LOS ESTADOS LÍMITE EN LOS REGISTROS DE DEFORMACIONES UNITARIAS
En la Figura 6, se presentan algunas respuestas en términos de deformaciones unitarias de la base de los muros estructurales en ambos sectores extremos (S1 y S2), para los modelos con IT 1.0, IT 1.2 e IT 1.4. Se usa el registro de Loma Prieta con diferentes niveles de intensidad del suelo con la finalidad de encontrar los valores de la Sa (T1,5%) que provoquen la fluencia, servicio y colapso en alguno de los muros estructurales. Los valores de Sa (T1,5%) que alcanzan la fluencia son: 0,1 (g), 0,075 (g) y 0,07 (g) para los modelos con IT 1.0, IT 1.2 e IT 1.4, respectivamente. Los valores de Sa(T1,5%) que alcanzan el servicio son: 0,75 (g), 0,44 (g) y 0,35 (g) para los modelos con IT 1.0, IT 1.2 e IT 1.4, respectivamente. Los valores de Sa (T1,5%) que alcanzan el colapso son: 3,1 (g), 1,18 (g) y 1,17 (g) para los modelos con IT 1.0, IT 1.2 e IT 1.4, respectivamente.
Todas las gráficas de la Figura 6 presentan el momento en que se alcanza un valor de deformación unitaria igual a 0,05; valor al cual se ha definido como estado límite de colapso. Adicionalmente, se verificó que el mayor valor de deformación unitaria se presenta en la base del muro estructural.
9. ANÁLISIS DINÁMICO INCREMENTAL
El Análisis Dinámico Incremental (IDA, siglas en inglés) es un estudio paramétrico utilizado para evaluar el desempeño sísmico de una estructura. Para realizar el IDA es necesario tener uno o varios registros sísmicos que serán escalados a diferentes niveles de medida de intensidad (MI) de la aceleración máxima del terreno (Vamvatsikos & Allin Cornell, 2002). El IDA es una metodología usada para verificar como varía algún parámetro de demanda ingenieril según la intensidad del registro símico. Mediante el uso del análisis no lineal dinámico se calcula algún parámetro de demanda ingenieril (EDP), el cual servirá de referencia para la evaluación de la estructura ante los diferentes niveles de intensidad establecidos. Finalmente, se procede a graficar los valores de EDP obtenidos dado una MI y se obtiene las curvas IDA.
Las diferentes medidas de intensidad pueden ser representadas por: PGA (aceleración máxima del terreno), PGV (velocidad máxima del terreno), Sa (T1,5%) (aceleración espectral con un amortiguamiento del 5% correspondiente al periodo del primer modo de vibración). Los parámetros de demanda ingenieril pueden ser los siguientes: derivas de piso, derivas totales,
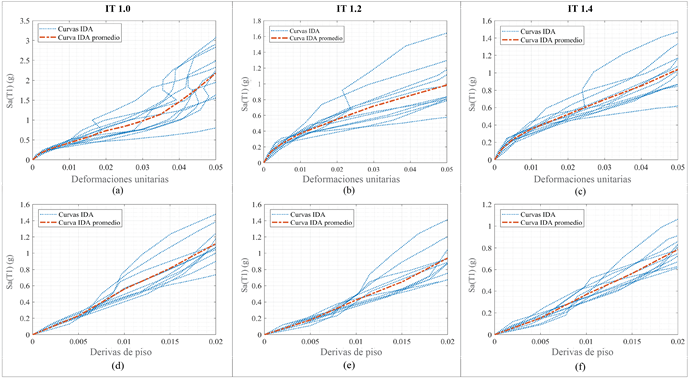
Figura 7 Curvas IDA de los tres arquetipos con diferentes EDP: (a) Modelo IT 1.0 y EDP de deformaciones unitarias, (b) Modelo IT 1.2 y EDP de deformaciones unitarias, (c) Modelo IT 1.4 y EDP de deformaciones unitarias, (d) Modelo IT 1.0 y EDP de deriva de piso, (e) Modelo IT 1.2 y EDP de deriva de piso, y (f) Modelo IT 1.4 y EDP de deriva de piso
deformaciones unitarias, corte basal, rotaciones nodales e índice de daño. En el presente estudio, se usa como MI a la Sa(T1,5%) y como EDP a las derivas de piso y deformaciones unitarias.
9.1 Curvas IDA
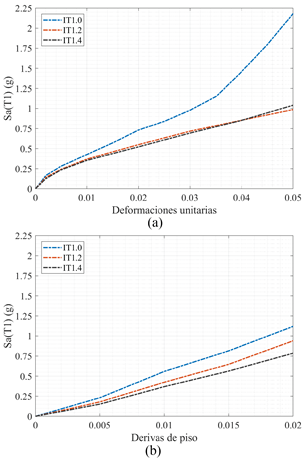
En la Figura 7, se presenta el grupo de curvas IDA para los diferentes arquetipos evaluadas con diferentes EDP (deformaciones unitarias y derivas de piso). Se puede observar que mientras aumenta el nivel de IT, las pendientes de las curvas IDA y los valores máximos de Sa(T1,5%) disminuyen. Se comprueba que el modelo IT 1.0 presenta el estado límite de colapso con valores de deriva de piso mayores al 2 %, si la evaluación estructural es con EDP de deformaciones unitarias. En el modelo IT 1.0, solo con 45,4 % de los registros se presenta el estado límite de colapso cuando las derivas de piso se encuentran entre 2,0 % y 3,5 % (ver Figura 8). La máxima Sa(T1,5%) promedio evaluada con deformaciones unitarias (2,18 g) es mayor que la máxima Sa(T1,5%) promedio evaluada con derivas de piso (1,12 g) (ver Figura 7(a) y Figura 7(d)). Esto sucede debido a que el estado límite de colapso de la estructura se presenta con valores de derivas mayores al 2% y valores de pseudo aceleración espectral mayores a 1,12 (g).
En el modelo IT 1.2 varios registros presentan el colapso antes de un valor de deriva de piso del 2 %. En este modelo con el 100 % de los registros, se presenta el estado límite de colapso cuando las derivas de piso se encuentran entre 2,0 % y 3,5 % (ver Figura 8). La máxima Sa(T1,5%) promedio evaluada con deformaciones unitarias (0,99 g) es mayor a la máxima Sa(T1,5%) evaluada con derivas de piso (0,94 g) (ver Figura 7(b) y Figura 7(e)).
Cuando el valor de la IT es mayor a 1,4, más del 90% de los registros logran esforzar a la estructura hasta alcanzar un estado límite de colapso cuando el valor de la deriva de piso se encuentra entre 2,0 % y 3,5 % (Ver Figura 8). Para el modelo IT 1.4, el valor máximo de Sa(T1,5%) promedio obtenido con deformaciones unitarias (1,04 g) es mayor que el valor máximo Sa(T1,5%) promedio obtenido con un EDP de derivas (0,79 g) (ver Figura 7(c) y Figura 7(f)). En todos los casos el valor promedio máximo de Sa(T1,5%) se encuentra en las curvas IDA elaboradas con un EDP de deformaciones unitarias.
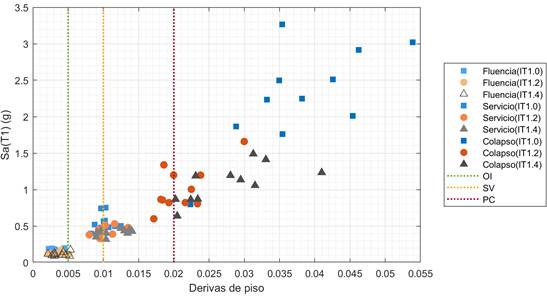
En la Figura 8, se grafican los valores de Sa(T1,5%) y derivas de piso a los cuales se presentan los estados límites de fluencia, servicio y colapso. Se puede observar que los puntos de fluencia se presentan antes de alcanzar un valor de deriva de piso igual a 0,5 %. El estado límite de servicio se presenta cuando la deriva de piso es alrededor del 1,0% y la mayor parte de puntos de colapso se encuentran luego de alcanzar una deriva de piso igual al 2,0 %. Tomando en cuenta que los valores de deriva de piso de 0,5 %, 1,0 % y 2,0% representan un nivel de desempeño según el FEMA 356, se procedió a relacionar el estado límite de fluencia con el nivel de desempeño de OI, el estado límite de servicio con el nivel de desempeño de SV y el estado límite de colapso con el nivel de desempeño de PC. De esta manera, se elaborará las curvas de fragilidad para los diferentes niveles de desempeño (OI, SV y PC), pero basados en dos parámetros de evaluación: derivas de piso y deformaciones unitarias.
9.2 Comparación de curvas IDA promedio
Al comparar los valores máximos de Sa(T1,5%) promedio (evaluado con deformaciones unitarias) de los tres modelos analizados, se puede observar que la curva correspondiente al modelo con IT 1.0 presenta valores de Sa (T1,5%) 2,20 y 2,09 veces mayor que los modelos con IT 1.2 y IT 1.4, respectivamente (ver Figura 9(a)). Además, las curvas IDA promedio de los modelos con IT 1.2 y IT 1.4 presentan una pendiente similar pero menor a la pendiente de la curva del modelo IT 1.0.
El valor máximo de Sa(T1,5%) que produce el nivel de desempeño de prevención de colapso en las curvas IDA promedio (evaluadas con derivas de piso) del modelo IT 1.0 es 1,19 y 1,42 veces mayor que el valor obtenido con los modelos IT 1.2 y IT 1.4, respectivamente (ver Figura 9(b)). Todos los modelos presentan curvas IDA promedio con diferentes pendientes. Adicionalmente, el modelo con IT 1.4 es el que menor valor de Sa (T1,5%) promedio alcanza cuando la deriva tiene un valor igual a 2 %.
10. CURVAS DE FRAGILIDAD
Vielma et al (2014) mencionan que las curvas de fragilidad permiten establecer la probabilidad que tiene una estructura o un elemento de exceder cierto estado límite de daño ante alguna acción sísmica. Los estados límites de daño pueden ser cuantificados por derivas de piso, deformaciones unitarias, o aceleraciones de piso. La función de fragilidad está representada por una distribución acumulativa log normal. La siguiente expresión (Ecuación (2)) representa la función de fragilidad:
Donde el valor de la mediana de la distribución de probabilidad es representado por θ; β es la desviación estándar logarítmica; Ф representa la función de la distribución acumulativa estándar; 𝐹 𝑖 (𝐷) representa la probabilidad condicional de que un elemento sea dañado y D es el parámetro de demanda ingenieril (FEMA P-58, 2018).
La Figura 10 presenta las curvas de fragilidad de los diferentes arquetipos, pero tomando en cuenta dos distintas medidas de daño (derivas de piso y deformaciones unitarias). Figura 10(a) y Figura 10(d) muestran las curvas de fragilidad para un nivel de desempeño de ocupación inmediata (OI) evaluadas con deformaciones unitarias y derivas de piso. La Figura 10(b) y Figura 10(e) muestran las curvas de fragilidad para un nivel de desempeño de seguridad de vida (SV). La Figura 10(c) y Figura 10(f) grafican las curvas de fragilidad para un nivel de desempeño de prevención de colapso (PC) evaluadas con las diferentes medidas de daño (MD) anteriormente mencionadas.
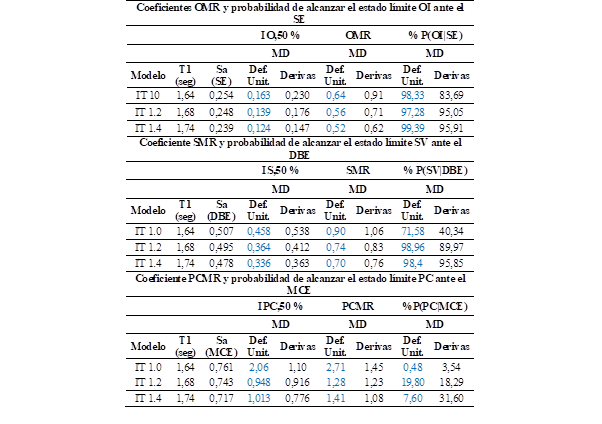
La Tabla 4 (Ver Anexo) muestra el coeficiente de margen de ocupación inmediata (OMR), coeficiente de margen de seguridad de vida (SMR) y coeficiente de margen de prevención de colapso (PCMR). Los coeficientes de margen representan la razón entre la intensidad de OI mediana, la intensidad de SV mediana o la intensidad de PC mediana y la aceleración espectral del periodo fundamental de la estructura ante el SE, DBE o MCE, respectivamente (FEMA, 2010). Los valores de intensidad mediana (IO,50%; IS,50%; IPC,50%) representan el valor de la pseudo aceleración espectral a la cual el 50 % de los registros alcanzan un determinado nivel de desempeño. En los tres modelos analizados, se puede observar que las curvas de fragilidad para un nivel de desempeño de OI y SV presentan una mayor probabilidad de alcanzar dicho estado límite, si la evaluación de las curvas IDA se las realiza con la MD de deformaciones unitarias (ver Figura 10(a), Figura 10(b), Figura 10(d) y Figura 10(e)).
Las curvas de fragilidad para el estado límite de PC presentan una mayor probabilidad de alcanzar dicho estado límite, si la evaluación se la realiza con la MD de derivas de piso (ver Figura 10(c) y Figura 10(f)). En la Figura 10(a) y Figura 10(b) se puede observar que el modelo IT 1.4 es el más propenso a alcanzar los estados límites OI y SV, si el parámetro de evaluación es la deformación unitaria. Cuando el parámetro de evaluación es la deriva de piso, el modelo IT 1.4 es el más propenso a alcanzar todos los estados límites (Ver Figura 10(d), Figura 10(e) y Figura 10(f)).
Los coeficientes OMR de cada uno de los arquetipos disminuyen mientras aumenta el nivel de irregularidad torsional (Ver Anexo, Tabla 4). Además, el modelo IT 1.4 es el modelo que mayor P(OI|SE) (probabilidad de alcanzar el estado límite de Ocupación Inmediata ante el Sismo de Servicio) presenta de los tres arquetipos. La Tabla 4 (Ver Anexo) también muestra los coeficientes SMR de los tres arquetipos al ser evaluados ante el sismo de diseño (DBE). Se puede verificar que mientras aumenta el nivel de irregularidad torsional los coeficientes SMR disminuyen. Por ejemplo, los modelos IT 1.2 e IT 1.4 (evaluados con deformaciones unitarias) presentan una disminución del 18,6% y 22,19% de su coeficiente SMR con respecto al modelo IT 1.0. Además, se muestra que mientras mayor es el nivel de irregularidad torsional mayor es la probabilidad de alcanzar el estado límite de SV. Por ejemplo, la P(SV|DBE) (probabilidad de alcanzar el estado límite de Seguridad de Vida ante el Sismo de Diseño) del modelo IT 1.2 es 1,38 y 2,23 veces más grande que la probabilidad del modelo IT 1.0, y la P(SV|DBE) del modelo IT 1.4 es 1,37 y 2,37 veces más grande que la del modelo IT 1.0.
Los coeficientes PCMR de los tres arquetipos fueron evaluados ante el MCE (Ver Anexo, Tabla 4). Se verifica que mientras aumenta el nivel de irregularidad torsional los coeficientes PCMR disminuyen. Por ejemplo, los modelos IT 1.2 e IT 1.4 (evaluados con derivas de piso) presentan una disminución del 14,71 % y 25,17 % de su coeficiente PCMR con respecto al modelo IT 1.0. Adicionalmente, se muestra la variabilidad de la probabilidad de prevención de colapso ante diferentes niveles de irregularidad torsional. El modelo IT 1.2 evaluado con deformaciones unitarias tiene la mayor P(PC|MCE) (probabilidad de alcanzar el estado límite de Prevención de Colapso ante el Sismo Máximo Considerable) entre el modelo IT 1.0 e IT 1.4. Cuando la evaluación se realiza por medio de derivas de piso el modelo IT 1.4 es el más crítico, ya que tiene una P(PC|MCE) 8,92 veces más grande que la probabilidad del modelo IT 1.0. De forma general, se puede verificar que la variación de la irregularidad torsional aumenta la probabilidad de alcanzar el estado límite de prevención de colapso.
Finalmente, se determina la probabilidad de alcanzar el estado límite de prevención de colapso ante el sismo de diseño (DBE). Dicha probabilidad resulta ser máximo 1,19% entre todos los arquetipos con ambas medidas de daño.
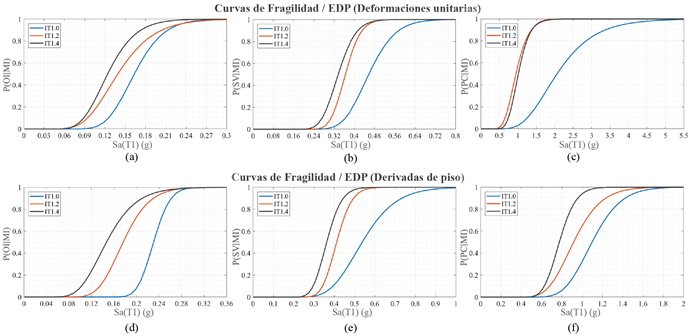
Figura 10 Curvas de fragilidad para los tres arquetipos: (a) Ocupación Inmediata, EDP: deformaciones unitarias, (b) Seguridad de Vida, EDP: deformaciones unitarias, (c) Prevención de Colapso, EDP: deformaciones unitarias, (d) Ocupación Inmediata, EDP: derivas de piso, (e) Seguridad de vida, EDP: derivas de piso, y (f) Prevención de Colapso, EDP: derivas de piso
11. CONCLUSIONES
Con la finalidad de verificar la variabilidad del desempeño sísmico ante la variación del nivel de irregularidad torsional, se desarrolló tres modelos no lineales los cuales fueron evaluados ante once registros sísmicos. Las derivas de piso y deformaciones unitarias fueron tomadas como parámetros de demanda ingenieril y medidas de daño. Por medio del procedimiento IDA se obtuvo el grupo de curvas IDA de cada uno de los arquetipos con los dos diferentes parámetros de demanda ingenieril. Finalmente, se relacionan los diferentes estados límite con los niveles de desempeño, y se crean curvas de fragilidad dependiendo del nivel de irregularidad torsional y medida de daño. A continuación, se describen los principales hallazgos:
Por medio de los análisis estáticos y dinámicos no lineales, se comprobó que en los modelos con IT 1.2 e IT 1.4 existe una redistribución de esfuerzos entre los elementos resistentes a carga lateral, siendo unos elementos más esforzados que otros. Además, se comprobó que al aumentar el nivel de irregularidad torsional las respuestas globales (derivas de piso) y demandas locales (momento, corte, deformaciones unitarias) aumentan.
Por medio de las curvas IDA, se comprobó que el modelo IT 1.0 logra alcanzar valores más altos de pseudo aceleración espectral (Sa (T1,5%)) con respecto a los modelos con IT 1.2 e IT 1.4. Además, se evidenció que mientras aumenta el nivel de irregularidad torsional disminuye las pendientes de las curvas IDA.
Al comparar las curvas de fragilidad con las diferentes medidas de daño, se concluye que la evaluación con deformaciones unitarias para los niveles de desempeño de Ocupación Inmediata y Seguridad de Vida, resultan ser más conservadoras, ya que es posible alcanzar dichos niveles de desempeño con menores Sa(T1,5%). Para el nivel de desempeño de Prevención de Colapso, la medida de daño de deriva de piso resulta ser la más crítica, ya que solo el 27 % de los análisis obtuvieron valores de derivas de piso cercanos o iguales al 2,0% cuando se presenta el estado límite de colapso.
Se concluye que a mayor nivel de irregularidad torsional mayor es la probabilidad de alcanzar el nivel de desempeño de prevención de colapso. Las probabilidades de alcanzar el nivel de desempeño de prevención de colapso ante el sismo máximo considerable para los modelos IT 1.2 e IT 1.4 son 18,29 % y 31,60 %, respectivamente; mientras que el modelo IT 1.0 solo tiene una probabilidad del 3,54 % de alcanzar el nivel de desempeño de prevención de colapso. Se verificó que el nivel de irregularidad torsional mayor a 1,4 aumenta la probabilidad de alcanzar el nivel de prevención de colapso 8,92 veces más que el modelo con irregularidad torsional igual a 1,0.
Al evaluar la probabilidad de alcanzar el estado límite de Seguridad de Vida ante el Sismo de diseño, nuevamente se verificó que el nivel de irregularidad torsional incrementa la probabilidad de alcanzar dicho estado límite. El modelo IT 1.0 tiene una probabilidad del 40,34 %, mientras que el modelo IT 1.4 tiene una probabilidad del 95,85 % de alcanzar el estado límite de Seguridad de Vida.
Finalmente, se concluye que el nivel de irregularidad torsional afecta al desempeño estructural, por lo tanto, es importante tener un nivel de irregularidad torsional máximo permisible que permita tener estructuras con bajas probabilidades de alcanzar el nivel de desempeño de prevención de colapso.