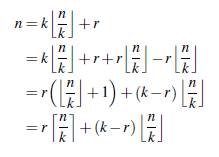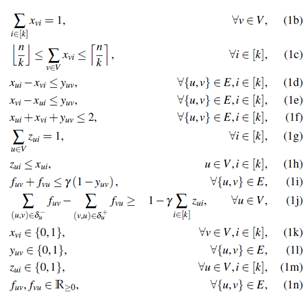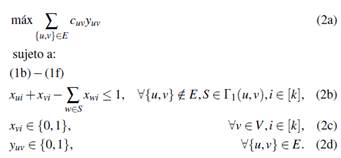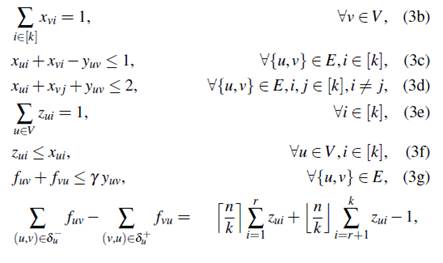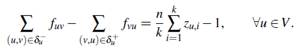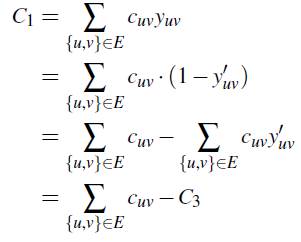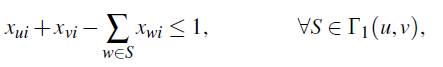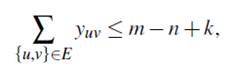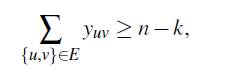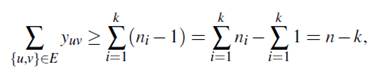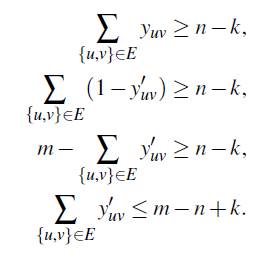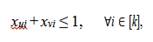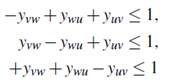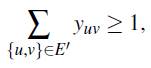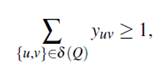INTRODUCCIÓN

Una tarea frecuente en múltiples áreas consiste en particionar un conjunto de objetos en varios subconjuntos tal que cada subconjunto cumpla con ciertos requerimientos como número mínimo o máximo de elementos u homogeneidad sobre los atributos cuantificados. Al asociar los objetos a nodos, la relación entre pares de objetos con la existencia de una arista y la similitud o disimilitud con una función de costo sobre dichas aristas, se podría pensar que el problema puede ser modelado usando teoría de grafos.

Un problema específico consiste en particionar el conjunto de nodos de un grafo de modo que el número de nodos en cada partición no exceda al resto de partes en más de una unidad y que en cada parte exista al menos un camino entre cada par de nodos. A esta variante se la conoce como el problema de k-equiparticionamiento en componentes conexas. Enfrentar este problema desde el punto de vista matemático es una tarea compleja, ya que se conoce que es un problema NP-duro, incluso en el caso en el de que se elimine la restricción de la cantidad de nodos en cada subconjunto de la partición (, ).

El problema de particionamiento de grafos ha sido ampliamente aplicado en diferentes campos, tales como procesamiento de imágenes (, ), diseño de distritos territoriales y políticos (, ), procesamiento en paralelo ( , ), diseño de circuitos VLSI (, ), deportes (, ), entre otros. Múltiples aplicaciones y una completa revisión bibliográfica del problema de particionamiento de grafos pueden ser encontradas en () y ().

El problema de particionamiento de grafos ha sido ampliamente estudiado y diferentes técnicas han sido usadas para su solución. Por ejemplo, () presentaron un método heurístico que permite particionar grafos arbitrarios con costos sobre las aristas en subconjuntos de nodos de tamaño conocido. Extensiones del trabajo anterior pueden ser encontradas en métodos heurísticos recientes como METIS (, ) o Kahip (, ) que permiten particionar grafos de gran tamaño considerando costos sobre las aristas y múltiples pesos sobre los nodos. Mediante el uso de la programación cuadrática, () reportaron un modelo que utiliza variables binarias e incluyeron varias reformulaciones y métodos de solución para aplicaciones prácticas. Con la aplicación de la programación semidefinida, () propone una nueva relajación para el problema de particionamiento general de grafos y compara los resultados teóricos y numéricos con trabajos previos. Por otro lado, () reportan una heurística de ordenamiento glotón basado en particionamiento espectral, donde los vectores propios del grafo son usados para construir una representación geométrica del mismo.

Nuestro interés se enfoca en métodos exactos basados en programación lineal entera. Así, () estudian el problema sobre grafos completos introduciendo el problema de particionamiento en cliques, donde los autores proponen una formulación lineal y un algoritmo tipo Branch & Cut. Enfocados en el problema anterior, () imponen restricciones de tamaño sobre el número de nodos en cada conjunto de la partición y aportan con un estudio poliedral del mismo. () presentaron un modelo de programación lineal entera para el problema de k-particionamiento junto con varias familias de desigualdades válidas y facetas para el poliedro asociado. En el caso de que se fije el número de particiones a dos, el problema de bisección puede ser identificado en ().

Requerimientos de conectividad son frecuentes en múltiples trabajos reportados en la literatura. Por ejemplo, () estudian desigualdades válidas que inducen facetas para el problema de encontrar el subgrafo conexo con peso máximo en un grafo. () proveen de condiciones necesarias para obtener conexidad en un subgrafo y de una herramienta para identificar si un grafo admite un particionamiento donde el peso en cada partición no exceda un valor fijo y se induzca un subgrafo conexo. Para el caso que se requiere particionar un grafo en componentes conexas, () buscan maximizar los costos de las aristas que pertenecen al corte. Los autores utilizan variables binarias para la elección de los arcos usados en la solución y variables continuas de flujo para garantizar la conexidad de las componentes. Adicionalmente, () plantean dos formulaciones para una versión del k-particionamiento conexo balanceado, es decir, se busca particionar un grafo con pesos sobre los nodos en un número fijo de componentes conexas de pesos similares. Los autores proponen una formulación basada en conjuntos separadores que incluye un gran número de restricciones que potencialmente pueden ser implementadas en tiempo polinomial. El trabajo anterior es complementado con una segunda formulación basada en flujos.

El problema de equiparticionamiento en componentes conexas usando Programación Lineal Entera es estudiado en este artículo, donde tres formulaciones para resolver el problema junto con varias familias de desigualdades válidas para el poliedro asociado son propuestas. Las desigualdades encontradas fueron incluidas como cortes en un algoritmo exacto de solución tipo Branch & Cut y son probadas en varias instancias simuladas.

El presente trabajo se encuentra organizado de la siguiente forma: En la Sección se introduce la notación y tres modelos de programación lineal entera mixta que describen el problema del equiparticionamiento de grafos en k−componentes conexas. En la Sección se detallan varias familias de desigualdades válidas para las formulaciones diseñadas. Finalmente, en la Sección se exponen amplia- mente los resultados computacionales obtenidos.

Notación y formulaciones enteras

Notación

Sea G = (V , E) un grafo no dirigido, donde V = {1, . . . , n} es el conjunto de nodos y E ⊂ {{i, j} : i, j ∈ V , i ̸= j} es el conjunto de aristas. Además, sobre el conjunto de aristas se define una función de costos d: E → R⁺ y sea k un entero mayor o igual a dos que denota el número de componentes en las que será particionado el grafo G. Notaremos por [k] = {1, . . . , k}.

Sobre un grafo G, se define un camino P de v ₁ a v _k (v ₁-v _k -path) como una secuencia v ₁, v ₂, ..., v _k ∈ V tal que {v _i , v _i+1 } ∈ E para i = 1, . . . , k − 1 y k ≥ 0. El número de aristas en P se conoce como la longitud del camino. Así, para dos nodos u, v ∈ V se define d(u, v) como la longitud más corta desde el nodo u hasta el nodo v. El grafo G es llamado conexo si existe un u-v-path, para todo u, v ∈ V . Por otro lado, para un subconjunto de nodos X ⊂ V , se define el conjunto de aristas δ (X ) = {{u, v} ∈ E: u ∈ X , v ∈ V \ X } también llamado el corte de X . Si tomamos un subconjunto X ⊂ V , entonces podemos ver que si eliminamos el conjunto de aristas δ (X) se generan al menos dos componentes conexas.

Lo anterior nos permite definir la idea de conjuntos separadores. Sea u, v ∈ V dos nodos no adyacentes de G, entonces diremos que el conjunto X ⊂ V \ {u, v} es un (u, v)-separador si u y v pertenecen a diferentes componentes conexas en el subgrafo inducido por V \ X . Si el nodo w es el único elemento del conjunto separador, entonces diremos que w es un nodo de articulación. Se define Γ₁(u, v) como el conjunto de todos los (u, v)-separadores de cardinalidad mínima en G.

El problema de equiparticionamiento en componentes conexas (PE C C ) consiste en encontrar una k-partición {V ₁,V ₂, . . . ,V _k } tal que cada subconjunto V _i induce una componente conexa, ⌊n/k⌋ ≤ |V _i | ≤ ⌈n/k⌉, y el costo total de las aristas en la misma componente es minimizado.

Es fácil notar que, si el número de particiones divide exactamente al número de nodos del grafo, todas las particiones tendrán n/k nodos. Por otro lado, si dicha división no es exacta, entonces existirá una o varias particiones que posean un nodo adicional. El siguiente resultado permite conocer el número de nodos contenidos en cada subconjunto de la partición.

Teorema 1. Dado un grafo G = (V , E), un entero k ≥ 2 y r = n mod k. Entonces en una k− partición se tienen r componentes con [n/k] nodos y k − r componentes con [n/k] nodos.

Demostración. Si se tiene que k divide exactamente a n, entonces r = 0 y cada componentes contiene n/k nodos y el resultado es trivial. Por otro lado, si n/k no es entero, entonces existen dos números enteros q y r tal que n = kq + r y r < k. Ahora, si tomamos q = [n/k] tenemos que:

Esto implica que el conjunto de n nodos puede ser particionado en r subconjuntos de tamaño [n/k] y k − r subconjuntos de tamaño [n/k], demostrando el teorema.

Primer modelo

Para el primer modelo es necesario construir la versión dirigida del grafo de entrada. Así, sea G = (V , E) un grafo no dirigido y se define el digrafo D = (V , A) que dispone del mismo conjunto de nodos y sus arcos son creados de la siguiente manera: si la arista {u, v} ∈ E, entonces los arcos anti-paralelos (u, v), (v, u) ∈ A, es decir, una arista del grafo original está asociada con dos arcos en el grafo dirigido. Sobre la versión dirigida se define δ u − como el conjunto de arcos salientes del nodo u, mientras que δ 𝑢 + representa el conjunto de arcos entrantes al nodo u.

El primer modelo dispone de las siguientes variables: Se definen las variables x _vi que toman el valor de uno si el nodo v pertenece a la partición i, o cero si esto no sucede, y variables y _uv que se les asigna un valor igual a uno si la arista {u, v} pertenece al corte, o toman el valor de cero si y solo si los vértices que unen la arista {u, v} son localizados en la misma partición. Para satisfacer el requerimiento de conexidad, se propone enviar unidades de flujo entre los nodos de la misma componente conexa. Para este efecto, definimos z _ui que toma el valor de uno si el nodo u es un nodo sumidero, o cero si no lo es. Además, sobre la versión dirigida se definen variables f _uv

que representan la cantidad de flujo sobre el arco (u, v) que debe ser un número real positivo incluido el cero. El modelo puede ser escrito de la siguiente forma (FG -1):

sujeto a:

donde γ = n−k+1.

La función objetivo () maximiza el costo total de las aristas en el corte, produciendo que las aristas de menor costo no sean seleccionadas y se ubiquen en los subgrafos inducidos por la partición. Se pueden identificar un bloque de restricciones que se concentran en equiparticionar el grafo. Así, () asegura que cada nodo sea asignado exactamente a un solo subconjunto, () limita la cantidad de nodos en cada subconjunto entre ⌊n/k⌋ y ⌈n/k⌉, () y () obligan a que si la arista {u, v} no pertenece al corte, entonces los nodos u y v se encuentren en el mismo subconjunto. Además, la restricción () afirma que si los nodos u y v se encuentran en la misma componente, entonces la arista {u, v} no debe encontrarse en el corte. Por otro lado, un segundo grupo de restricciones asegura la conexidad de la partición. Así, la restricción () exige que exactamente un solo nodo sea asignado como sumidero para cada subconjunto, mientras que () es una restricción de acoplamiento de variables e indica que únicamente los nodos que pertenecen a un subconjunto son candidatos para ser sumideros. Finalmente, las restricciones () y () permiten calcular el flujo en los arcos. En () se tiene que si la arista {u, v} pertenece al corte, entonces no debe existir un flujo por sus arcos asociados en el grafo dirigido. Por otro lado, si la arista no es asignada al corte, entonces puede existir flujo sobre dichos arcos y la suma no debe superar n − k + 1 unidades. Finalmente, () es una restricción de conservación de flujo. Las restricciones antes mencionadas producen que los nodos en un mismo subconjunto de la partición se encuentren conectados y se conviertan en componentes conexas a través del flujo. El primer modelo es derivado de ().

Segundo modelo

La siguiente formulación plantea modelar la conexidad usando conjuntos separadores. Las variables usadas en esta formulación están asociadas a los nodos y las aristas del grafo. La variable x _vi toman el valor de uno si el nodo v pertenece a la partición i, o cero en caso contrario, mientras que la variable y _uv toma en valor de uno si la arista {u, v} pertenece al corte, o cero en otro caso.

El segundo modelo para el problema de equiparticionamiento en componentes conexas (FG -2) puede ser escrito de la siguiente forma:

De forma similar que en el modelo FG -1, la función objetivo () maximiza las aristas del corte y las restricciones () - () buscan equiparticionar el grafo. Por otro lado, la restricción () impone que si dos nodos no adyacentes u, v ∈ V se encuentran en el mismo subconjunto, entonces necesariamente debe existir al menos un nodo de cada conjunto separador S ∈ Γ₁(u, v) en el mismo subconjunto para asegurar que exista comunicación entre ellos. Esta formulación desciende de ().

Tercer modelo

A diferencia de los modelos anteriores, en la presente sección se introduce una nueva formulación que considera desigualdades dife- rentes a las reportadas en la literatura que permiten modelar la conexidad de cada partición. Así, en este modelo se cambia el sentido de la optimización y se propone minimizar el costo total de las aristas en las componentes conexas. Este hecho provoca una modificación en la naturaleza de las variables asociadas a las aristas y se define y _uv = 1 si la arista {u, v} pertenece a alguna de las componentes conexas o y _uv = 0 en otro caso. Por el contrario, las variables binarias x _vi mantienen su interpretación y toman el valor de uno si el nodo v se encuentra en la partición i, o cero en caso contrario. Además, las variables z _ui identifican si el nodo u es un nodo fuente de la componente i y las variables f _uv representan la cantidad de flujo enviado por el arco (u, v) en la versión dirigida.

El modelo puede ser expresado de la siguiente forma (FG -3):

Sujeto a:

donde γ = n − k + 1 y r = n mod k.

La función objetivo () apunta a minimizar el costo total de las aristas con nodos finales en la misma componente conexa. La restricción () garantiza que cada nodo sea asignado exactamente a una sola componente conexa. La desigualdad () muestra que si dos nodos incidentes u y v son asignados a un mismo subconjunto, entonces la arista que los conecta debe ser incluida en la solución. Adicionalmente, en () se asegura que, si dos nodos incidentes se encuentran en diferentes subconjuntos de la partición, entonces la variable asociada a dicha arista debe tomar el valor de cero. Con estas dos últimas restricciones describimos completamente la relación existente entre nodos y aristas dentro y fuera de una componente conexa. La restricción () asigna un único nodo fuente en cada subconjunto de la partición, mientras que la restricción () permite a un nodo ser fuente si y solo si primero pertenece a dicho subconjunto. Finalmente, () es una restricción de conservación de flujo y muestra que se seleccionan r nodos fuente que envían

⌈n/k⌉− 1 unidades de flujo y k − r nodos fuente que envían ⌊n/k⌋− 1 unidades de flujo. Además, si un nodo no es fuente, entonces será un sumidero con demanda igual a una unidad. El lado derecho de la restricción claramente es justificado por el Teorema y es fácil ver que, si n divide exactamente a k, entonces r es igual a cero y la restricción () puede ser escrita de la siguiente forma:

2.5 Relaciones entre los modelos

Los siguientes resultados establecen una correspondencia entre el conjunto de puntos de los poliedros asociados a cada una de las formulaciones reportadas. Para ello, sean P¹ = {y ∈ {0, 1} ^|E| , x ∈ {0, 1} ^|V|×k , z ∈ {0, 1} ^|V|×k , f ∈ R_≥0: () - () son satisfechas}, P² = {y ∈ {0, 1} ^|E| , x ∈ {0, 1} ^|V|×k : () - () y () son satisfechas} y P³ = {y ∈ {0, 1} ^|E| , x ∈ {0, 1} ^|V|×k , z ∈ {0, 1} ^|V|×k , f ∈ R_≥0: () - () son satisfechas} los poliedros asociados a la formulación FG -1,FG -2 y FG -3, respectivamente.

Teorema 2. Un punto (x, y, z, f ) ∈ P¹ si y sólo si (x, y) ∈ P².

Demostración. Sea (x, y, z, f ) un punto en P¹ que genera una solución de costo C₁, entonces podemos elaborar una solución (x^′, y^′) para P² con costo C₂. Dado que las variables sobre nodos y aristas poseen la misma interpretación se tiene una relación directa, es decir, x^′ = x y y^′ = y. Notemos que, utilizando dicha relación, las variables x^′ satisfacen la restricción (), ya que x garantiza conectividad en P¹. Esto se tiene ya que si x^′ _ui = x^′ _vi = 1, para nodos u, v no adyacentes y algún i ∈ [k], entonces cualquier conjunto separador S debe contener al menos un nodo en V _i \ {u, v}, asegurando de este modo que ∑ _w∈S x^′ _wi ≥ 1 y por tanto el cumplimiento de la restricción mencionada. Además, se tiene que C₂ = C₁.

La otra implicación sigue inmediatamente tomando x = x^′, y = y^′ y seleccionando aleatoriamente un nodo sumidero en cada V _i , para i ∈ [k]. Finalmente, los valores de las variables de flujo pueden ser polinomialmente obtenidas asegurando la conservación de flujo sobre cada una de las componentes conexas.

Teorema 3. Un punto (x, y, z, f ) ∈ P¹ si y sólo si (x, 1 ^|E| − y, z, f ) ∈ P³.

Demostración. Sea (x, y, z, f ) un punto en P¹ que genera una solución de costo C₁, entonces podemos construir una solución (x^′, y^′, z^′, f ^′) para P³ con costo C₃. Así, se pueden encontrar las aristas en la solución de P³ tomando 𝑦 𝑢𝑣 ′ = 1 − y _uv para todo {u, v} ∈ E, y para los nodos utilizando 𝑥 𝑢𝑖 ′ = x _ui , para todo u ∈ V y i ∈ [k]. Además, los nodos fuente pueden ser identificados a partir de los nodos sumideros eligiendo 𝑧 𝑢𝑖 ′ = z _ui , para todo u ∈ V y i ∈ [k]. Finalmente, las variables f ^′ son reveladas mediante 𝑓 𝑢𝑣 ′ = f _vu para todo{u, v} ∈ E.

Adicionalmente, el valor de la función objetivo depende de las variables asociadas a las aristas y se tiene:

Por otro lado, si se dispone de un punto factible (x^′, y^′, z^′, f ^′) para P³ con costo C₃, se puede notar que mediante las igualdades anteriores es posible construir fácilmente un punto (x, y, z, f ) en P¹ con costo C₁.

Por el Teorema y se tiene el siguiente resultado:

Corolario 1. Un punto (x, y) ∈ P² si y sólo si (x, 1 ^|E| − y, z, f ) ∈ P³.

3. DESIGUALDADES VÁLIDAS

En esta sección, varias familias de desigualdades válidas asociadas a los poliedros del problema de equiparticionamiento de grafos en componentes conexas son presentadas. Los primeros resultados se derivan de las desigualdades válidas introducidas en () y ().

Teorema 4. Sea ℓ ∈ V un nodo de articulación y sean u, v ∈ V nodos en diferentes componentes conexas en el subgrafo inducido por V \ {ℓ}. Entonces las desigualdades:

x _ui + x _vi − x _ℓi ≤ 1, ∀i ∈ [k],

son válidas para FG -1 y FG -3.

El resultado anterior puede ser generalizado usando la noción de conjuntos separadores.

Teorema 5. Sean u y v dos nodos no adyacentes en V y Γ₁(u, v) sus conjuntos separadores. Entonces las desigualdades:

son válidas para FG -1 y FG -3.

El tercer tipo de desigualdades identifica el número mínimo de aristas necesarias para asegurar la conexidad de una solución factible, lo que permite mejorar la cota inferior de los distintos modelos. La desigualdad tiene la siguiente estructura:

Teorema 6. La desigualdad:

es válida para FG -1 y FG -2, y la desigualdad:

es válida para FG -3

Demostración. Sea n _i el número de nodos de la componente i, para i ∈ [k], tal que ∑ _i∈[k] n _i = n y (n/k) ≤ n _i ≤ (n/k). Es conocido que se necesitan al menos n _i − 1 aristas para que la componente i sea conexa. Para la formulación FG -3 se tiene:

es decir, se necesitan al menos n − k aristas para obtener un equiparticionamiento conexo. Por otro lado, las desigualdades para los casos de maximización (FG -1 y FG -2) se obtienen mediante las equivalencias del Teorema y del Corolario usando la relación y^′ = 1 ^|E| − y. Así,

El cuarto tipo de desigualdades identifica los pares de nodos que no pueden ser incluidos en la misma componente conexa. Puede se expresado por el siguiente resultado:

Teorema 7. Sean u y v dos nodos de G tal que d(u, v) ≥ ⌈n/k⌉, entonces las desigualdades:

son válidas para FG -1, FG -2 y FG -3.

Demostración. Tomemos dos nodos u y v, se conoce que el tamaño máximo de una componente es ⌈n/k⌉. Como se tiene que d(u, v) ≥⌈n/k⌉, entonces cualquier camino que permite conectar a los nodos u y v en el grafo utiliza al menos ⌈n/k⌉ aristas. Esto implica que, si alguna componente conexa contiene a los nodos u y v, entonces dicha componente debe tener al menos ⌈n/k⌉ + 1 nodos violando de este modo la condición de equipartición.

El quinto tipo se deriva de las desigualdades triangulares introducidas por (), que indican que, si tres nodos se encuentran dentro de un mismo subconjunto, entonces las aristas que los conectan también deben ser usadas en la solución. Así, dados tres nodos u, v, w ∈ V tal que {u, v},{v, w},{u, w} ∈ E, entonces las desigualdades:

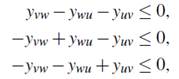son válidas para FG -3. Utilizando la equivalencia entre las formulaciones se tiene que:

son desigualdades válidas para FG -1 y FG -2.

El sexto tipo de desigualdades es útil en grafos densos. La idea consiste en identificar cliques con k + 1 nodos y por el hecho de que el grafo debe ser particionado en k componentes, entonces al menos 2 nodos de la clique deben ser asignados al mismo subconjunto. El resultado es presentado en el siguiente teorema:

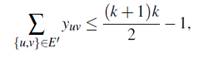Teorema 8. Sea T = (T ^′, E^′) una clique en G con |T ^′| = k + 1 nodos, entonces la desigualdad:

es válida para FG -1 y FG -2. Además, la desigualdad:

es válida para FG -3.

Demostración. Sea T = (T ^′, E^′) una clique con k + 1 nodos contenida en G . Es fácil notar que jamás podría presentarse el caso de que los nodos de la clique sean asignados a componentes diferentes ya que se tiene k + 1 nodos en T ^′ y tan solo k subconjuntos en los que debe ser particionado el conjunto de nodos. Esto implica que al menos dos nodos en T ^′ deben ir juntos en una misma componente conexa, es decir, al menos una arista perteneciente a E^′ debe ser elegida en la solución. Para la formulación FG -3 se tiene:

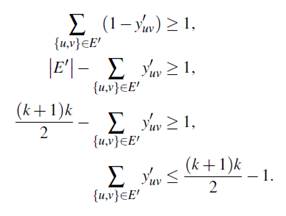
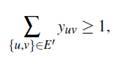Las desigualdades para los casos de maximización (FG -1 y FG -2) se obtienen mediante las equivalencias del Teorema . Así,

Las desigualdades del anterior tipo pueden ser separadas por un algoritmo de fuerza bruta en un tiempo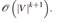

El último tipo de desigualdades válidas se centran en eliminar subconjuntos de nodos que no satisfacen las condiciones de equiparticionamiento, es decir, realizar una búsqueda de aquellos subconjuntos que disponen de máximo ⌊n/k⌋ − 1 nodos y asegurar que exista una arista en el corte para garantizar la conexidad de la solución. El resultado es formalizado de la siguiente forma:

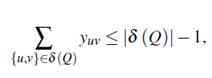Teorema 9. Sea Q ⊂ V tal que 1 ≤ |Q| ≤ ⌊n/k⌋ − 1, entonces la desigualdad:

es válida para FG -1 y FG -2. Además, la desigualdad:

es válida para FG -3.

Demostración. Sea Q ⊂ V tal que 1 ≤ |Q| ≤ ⌊n/k⌋ − 1. Dado que cada componente debe tener al menos ⌊n/k⌋ nodos, entonces al menos un nodo en la vecindad debe ser incluido en el conjunto Q para alcanzar el número mínimo de nodos en la componente conexa y satisfacer la condición de equipartición. Esto implica que para la formulación FG -3 debe existir al menos una arista en el corte de 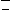Q. Por otro lado, para las formulaciones FG -1 y FG -2 se puede usar el mismo argumento, es decir, para asegurar que el conjunto Q se transforme en una componente conexa, a lo más |δ (Q)| − 1 aristas deben ser incluidas en el corte. Si Q contiene nodos de varios subconjuntos de la partición, entonces más de una arista en δ (Q) será incluida en la solución.

4. RESULTADOS COMPUTACIONALES

En esta sección, se reportan los resultados computacionales obtenidos con las formulaciones FG -1, FG -2, y FG -3 junto con las desigualdades válidas reportadas en el presente trabajo. Todos los experimentos computacionales fueron realizados en un computador Intel Core i7-9700K CPU 3.60 Ghz con 32 GB de memoria RAM bajo el sistema operativo Windows 10 Education. Además, se utilizó la versión 9.1.1 del solver de optimización Gurobi (, ) a través de la distribución Anaconda. Adicionalmente, se programó en la aplicación Jupyter Notebook mediante el lenguaje de programación Python.

Las instancias utilizadas fueron simuladas de la siguiente forma: se generaron aleatoriamente n puntos (x, y) en el plano, donde x ∈ [0; 200] e y ∈ [0; 200]. La posición de cada nodo fue asociada a cada punto (x, y). Para cada par de puntos u, v ∈ V con u ̸= v, se generó una arista con costo c _uv igual a la distancia euclidiana entre los puntos extremos de dicha arista. Además, un número real en el intervalo [0, 1] fue considerado, de forma que la arista existe basada en una probabilidad igual a dicho valor. Dependiendo del número de aristas y nodos, diremos que el grafo generado tiene densidad igual a d = 2|E|/(|V |(|V | − 1)).

Iniciamos comparando los tamaños de los modelos, donde se puede notar que las formulaciones FG -1 y FG -3 dependen únicamente de n = |V | y m = |E| por lo que su tamaño crece polinomialmente en función de la instancia de entrada. Por otra parte, el modelo FG -2 precisa de la cardinalidad del conjunto Γ₁ lo que produce que el número de restricciones crezcan exponencialmente. La Tabla muestra los tamaños de los modelos, donde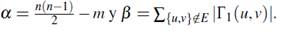

Tabla 1 Tamaño de los modelos 

Se plantea resolver los modelos enteros incluyendo diferentes configuraciones de desigualdades válidas y comparar sus comportamientos. Para las diferentes formulaciones se incluyeron las desigualdades de tipo: Separador (Teorema ), Cota (Teorema ), Camino (Teorema ), Clique (Teorema ), Corte (Teorema ) y Triángulo (desigualdades triangulares). Para todas las instancias, los algoritmos de separación utilizados son del tipo fuerza bruta y los cortes del solver Gurobi fueron deshabilitados. Es importante notar que el número de desigualdades de tipo Cota y Camino tienen un orden polinomial por lo que fueron añadidas en el nodo raíz. En la formulación FG -2, las restricciones relacionadas con los conjuntos separadores fueron incluidas como desigualdades tipo lazy.

En un primer experimento, se resolvieron los modelos FG -1, FG -2 y FG -3 sobre instancias pequeñas (n ≤ 20) con la finalidad de identificar la validez de las desigualdades reportadas y determinar el mejor comportamiento del algoritmo exacto de solución respecto al tiempo de ejecución, la cantidad de nodos explorados y el valor de la brecha de optimalidad.

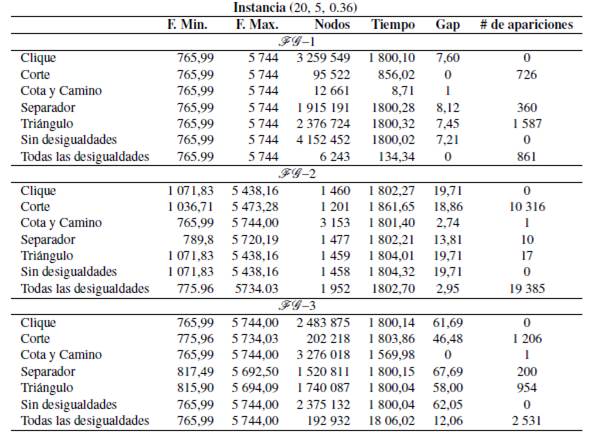
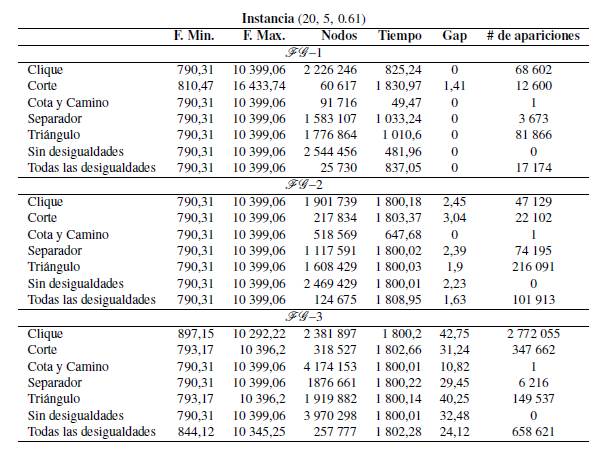
Para cada instancia (n, k, d) se reportan los experimentos utilizando varias configuraciones de desigualdades, con todas las desigualdades y sin usar ninguna de ellas. Las Tablas - reportan los resultados de cada caso y se encuentran organizadas de la siguiente forma: las dos primeras columnas reportan el valor de la función objetivo considerando el sentido de minimización y su valor equivalente en el sentido de maximización; las tres columnas siguientes indican el número de nodos explorados en el proceso de optimización, el tiempo de ejecución en segundos y la brecha de optimalidad en porcentaje. La última columna representa el número total de apariciones de todas las desigualdades válidas en cada experimento. El tiempo máximo de ejecución para los experimentos se fijó en 1800 segundos.

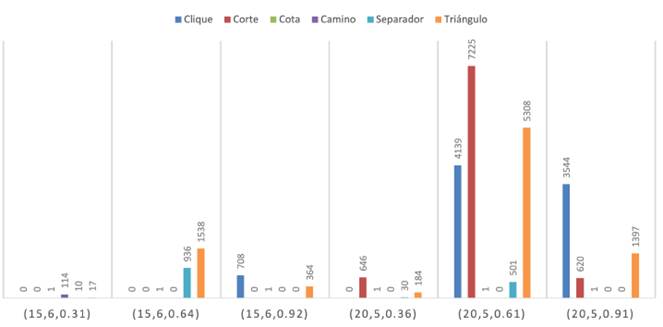
La diferencia en la densidad de los grafos de entrada permite evidenciar que las desigualdades tipo Camino aparecen cuando el grafo es disperso, mientras que las desigualdades tipo Clique surgen cuando el grafo es denso. Respecto a la desigualdad tipo Cota se puede ver que su inclusión es favorable, ya que genera una importante disminución en el tiempo de ejecución respecto al caso sin desigualdades. Usando las desigualdades tipo Separador, se evidencia la gran cantidad de desigualdades que son incluidas en una instancia, pero no tienen un efecto significativo en la solución. Las desigualdades tipo Triángulo no tienen un gran impacto en el tiempo de ejecución, pero en algunas instancias ayudan a encontrar la solución óptima explorando una menor cantidad de nodos. Además, es importante notar que en la gran mayoría de los modelos existe al menos una estrategia que mejora el tiempo de ejecución respecto al caso en el que no se incluyen desigualdades válidas, verificando la validez del método de solución diseñado en el presente trabajo. Para el modelo FG -1, la Figura muestra la distribución del número total de apariciones de los tipos de desigualdades válidas en las instancias consideradas en este experimento.

Por otro lado, podríamos afirmar que el modelo que mejor se comporta respecto al tiempo de ejecución en estas instancias es el modelo FG -1, ya que independientemente de la desigualdad aplicada y la densidad de la instancia, el algoritmo asociado termina en un menor tiempo comparado con los otros dos modelos. Además, podemos descartar al modelo FG -2 para el resto de experimentos, pues al depender de los conjuntos separadores, el tamaño del modelo crece al punto en que se vuelve computacionalmente intratable.

Adicionalmente, debido al número de elementos en el conjunto Γ₁ en instancias de mayor tamaño, las desigualdades válidas tipo Separador también las podemos excluir para los siguientes análisis.

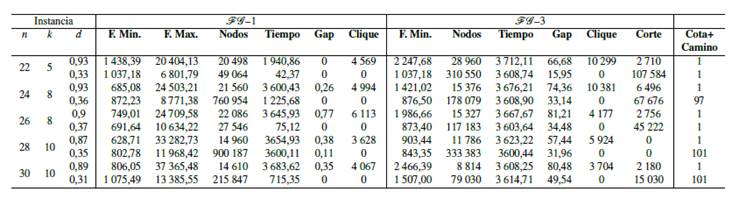
En un segundo experimento, se procede a resolver los modelos FG -1 y FG -3 sobre instancias de mayor tamaño, cada uno usando las estrategias que mejoran su eficiencia según los análisis anteriores. Las nuevas instancias consideran grafos con n ∈ {22, 24, 26, 28, 30} y la cantidad de subconjuntos en la que debe ser particionado el grafo varía entre 5 y 10. De la misma forma que en las instancias anteriores, se consideran experimentos con grafos usando densidad alta y baja, pues de esto depende la existencia de varios tipos de desigualdades. La Tabla reporta los resultados obtenidos para este experimento y se encuentra organizada de la siguiente forma: las tres primeras columnas muestran las características de la instancia (n, k, d); las siguientes seis columnas son asociadas al modelo FG -1 y reportan el valor de la función objetivo transformada al caso de minimización, el valor de la función objetivo, la cantidad de nodos explorados en el proceso de optimización, el tiempo de ejecución en segundos, la brecha de optimalidad y la cantidad de desigualdades tipo Clique incluidas en el proceso de solución; las subsiguientes seis columnas están asociados al modelo FG -3 e indican el valor de la función objetivo, la cantidad de nodos explorados en el proceso de optimización, el tiempo de ejecución en segundos, la brecha de optimalidad, el número de desigualdades tipo Clique y el número de desigualdades tipo Corte incluidas en el proceso de solución. Se aplicaron el mismo número de desigualdades válidas tipo Cota y Camino en ambos modelos en el nodo raíz y los valores se indican en la última columna. El tiempo máximo de ejecución para los experimentos mencionados se ha extendido a 3600 segundos.

Tabla 2 Comparación de los modelos FG -1, FG -2 y FG -3 con instancias de densidad baja 

Tabla 3 Comparación de los modelos FG -1, FG -2 y FG -3 con instancias de densidad media 

Tabla 4 Comparación de los modelos FG -1, FG -2 y FG -3 con instancias de densidad alta 

Figura 1 Distribución de apariciones de las desigualdades válidas en el modelo FG -1 

Tabla 5 Comparación de los modelos FG -1 y FG -3 

Al comparar los modelos FG -1 y FG -3 se puede observar un mejor comportamiento del modelo FG -1, ya que en muchas instancias se obtiene la solución óptima y en el resto de ellas el valor del gap se aproxima a cero. Por otro lado, la tercera formulación reporta altos valores del gap en todas las instancias, con un valor promedio del 52.52 %. Lo anterior nos permite concluir que el modelo FG -3 no presenta un desempeño satisfactorio para resolver el problema sobre instancias de mayor tamaño y es descartado para los siguientes experimentos.

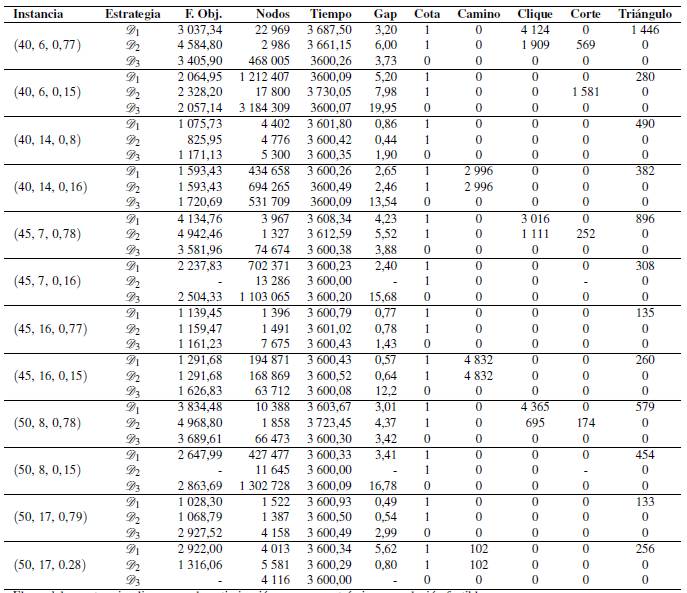
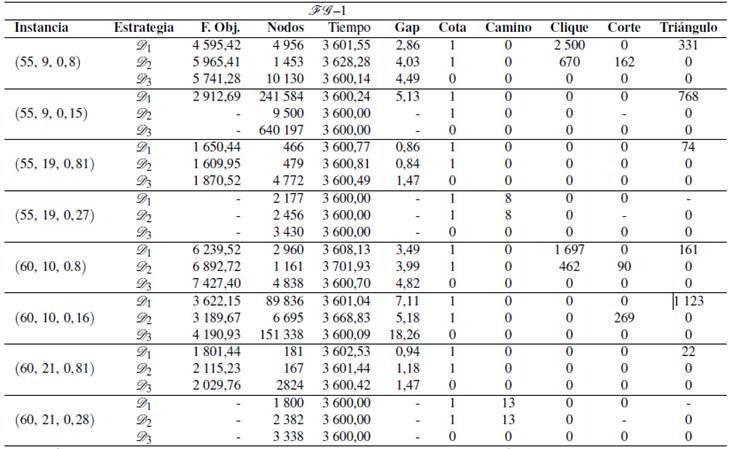
En las Tablas - , se reportan experimentos sobre instancias con grafos de 40 ≤ n ≤ 60 nodos y con 6 ≤ k ≤ 21 subconjuntos usando exclusivamente el modelo FG -1 bajo dos tipos de estrategias notadas por D₁ y D₂. En ambas estrategias, se incluyen las desigualdades tipo Cota, Camino y Clique, ya que en los experimentos anteriores disminuyeron la cantidad de nodos explorados y el tiempo de ejecución. Además, la estrategia D₁ admite la desigualdad tipo Triángulo, mientras que D₂ admite la desigualdad tipo Corte. Estas dos estrategias son comparadas con una tercera (D₃) en la que no se incluyen desigualdades válidas. Para cada instancia y estrategia, el valor de la función objetivo, el número de nodos explorados, el tiempo de ejecución en segundos, la brecha de optimalidad en porcentaje y el número de desigualdades de cada tipo incluidas en el proceso de solución son reportadas.

De las 20 instancias presentadas, dos de ellas no se resolvieron mediante ninguna estrategia. En 15 instancias sucedió que al- guna de las estrategias D₁ y D₂ reportó un mejor comportamiento que el caso sin desigualdades, ya que encontró una solución con menor valor en la función objetivo. En las tres instancias faltantes, el caso sin desigualdades obtuvo una mejor solución, pero en dos de ellos el valor del gap es mayor. Cabe notar que en la mayoría de las instancias, las estrategias D₁ y D₂ obtuvieron sus soluciones con menor cantidad de nodos explorados respecto al caso sin desigualdades. En los reportes anteriores, se evidencia que en instancias grandes las desigualdades válidas propuestas en el presente trabajo reducen el valor del gap y la 18/01 de nodos explorados. Comparando las estrategias D₁ y D₂, se muestra que D₁ en 12 ocasiones encontró una mejor solución con un menor valor del gap.

Tabla 6 Modelo FG -1 para grafos con n ∈ {40, 45, 50} 

El uso del caracter - implica que en la optimización no se encontró ninguna solución factible.

El uso del caracter - implica que en la optimización no se encontró ninguna solución factible.

Conclusiones

En este artículo se estudia el problema de equiparticionamiento de grafos en un número fijo de componentes conexas. El problema consiste en particionar un grafo no dirigido con costos sobre las aristas en un número fijo de componentes conexas, tal que el número de nodos en cada componente difiera en a lo más una unidad. El objetivo busca minimizar el costo total de las aristas con nodos finales en la misma componente. Tres modelos de programación lineal entera junto con varias familias de desigualdades válidas e incluidas en un algoritmo exacto tipo Branch & Cut fueron propuestos para resolver el problema. La efectividad de las desigualdades válidas fueron probadas computacionalmete al obtener una significativa reducción en el número de nodos explorados, tiempo de ejecución y brecha de optimalidad. Al comparar las tres formulaciones se pudo concluir que la formulación FG -1 es la que se comporta de mejor forma. Al igual que otros algoritmos exactos para el problema de particionamiento de grafos reportados previamente en la literatura, nuestro método permite resolver instancias de hasta 60 nodos.

Los resultados obtenidos muestran la funcionalidad del modelo FG -1 ya que se alcanzan valores cercanos al óptimo usando las distintas estrategias de solución D₁ y D₂. La brecha de optmalidad en promedio es igual al 3 % y en algunos casos menor que 1 %. Esto implica que se dispone de una formulación estable y un algoritmo exacto tipo Branch & Cut adecuado para resolver el problema de equiparticionamiento de grafos generales en componentes conexas.

Como trabajo futuro se podría pensar en mejorar las rutinas de separación y explorar otros tipos de desigualdades válidas para las formulaciones FG -2 y FG -3. Finalmente, este trabajo puede ser extendido a problemas de equiparticionamiento considerando pesos sobre los nodos, de modo que no solo se busque un equiparticionamiento, si no también se obtenga un balance respecto al peso impuesto sobre los nodos.