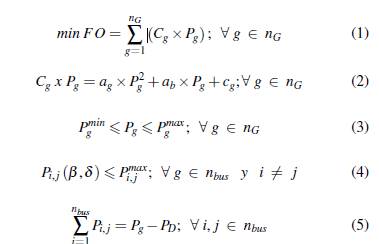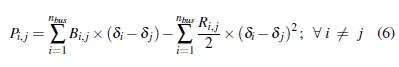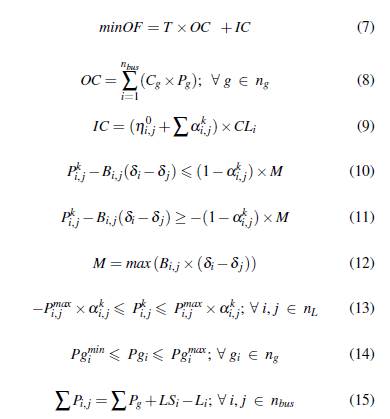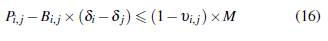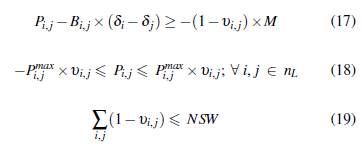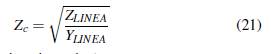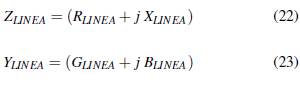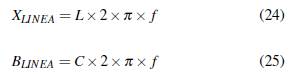INTRODUCCIÓN
En la actualidad, diferentes empresas que conforman el sector eléctrico han mantenido procesos de modernización y automatización del equipamiento de los sistemas de potencia y sistemas de distribución, lo cual deriva en la mejora de la infraestructura de los sistemas eléctricos (, ). Las empresas eléctricas, con la finalidad de mejorar la calidad de servicio eléctrico, han realizado diversas inversiones en sus sistemas eléctricos de potencia (SEP) buscando automatizar sus procesos de operación, lo cual les ha permitido tener control del equipamiento de corte y seccionamiento de forma remota, a través de un sistema SCADA, y de esta forma, reducir tiempos de respuesta ante contingencias o eventos de falla, permitiéndoles mejorar sus indicadores de calidad del servicio eléctrico.
Algunos SEP en condiciones normales operan con una topología en función de sus necesidades, manteniendo un esquema definido el cual puede variar ante contingencias. Uno de estos esquemas podría considerar que todas las líneas de transmisión se encuentren conectadas o energizadas, independiente de las condiciones de cargabilidad de los elementos del sistema de transmisión.
Si el SEP se ve afectado por una contingencia o falla eléctrica en la red de transmisión, se desconectarían líneas por la actuación del sistema de protecciones, ocasionando que las líneas de transmisión operativas experimenten incrementos en su cargabilidad, dicho escenario puede originar la desconexión de líneas adicionales por sobrecarga, lo que deriva en escenarios de desconexión de carga masiva y afecta directamente el servicio eléctrico.
Como se indicó anteriormente, los equipamientos que pueden verse afectados por exceso de cargabilidad en un SEP (, ) son las líneas de transmisión (LT), estas soportan incrementos súbitos de carga, debido a trasferencias de potencia o desconexión de equipos por cortocircuitos. Este tipo de maniobras manuales o automáticas permiten mantener la transmisión de energía, lo cual evita colapsos del sistema (Blackout).
En ese sentido, cabe indicar que los SEP son objeto de constante cambio debido a los requerimientos de la demanda, por lo que ca- da año es necesario repotenciar dicho sistema, instalando nuevas centrales de generación o líneas de transmisión, lo cual requiere la planificación de la expansión de la transmisión (TEP) (, ; , ). Esto conlleva a considerar algunas restricciones como por ejemplo la cargabilidad de las líneas de transmisión, perfiles de voltajes en las barras del sistema, desviación angular, balance de potencia y pérdidas del sistema, lo cual permite una operación segura y confiable del SEP ante probables escenarios de contingencia (, , b).
La TEP se puede considerar como un problema de optimización, el cual presenta una cantidad de variables de decisión que a través de una función objetivo, permite minimizar costos o maximizar los beneficios en función de un conjunto de restricciones, dichas restricciones permiten modelar criterios técnicos, económicos y de confiabilidad del SEP (, ).
Para la solución de la TEP, se han aplicado técnicas de optimización (, ; , ; , ; , ) tradicionales: la programación lineal, programación no lineal, programación dinámica y programación entera mixta; sin embargo, los mejores resultados se han obtenido cuando se aplican técnicas heurísticas y metaheurísticas (MH). Este tipo de metodologías al no ser matemáticamente robustas pueden presentar resultados no confiables para redes complejas, a pesar de esta falencia existen muchos trabajos de investigación que aplican modelos MH los cuales permiten encontrar soluciones alternativas a los problemas de optimización (, ; , ).
Con este antecedente, el presente estudio pretende desarrollar un modelo matemático que plantee una solución al problema de expansión de la transmisión en SEP aplicando conmutación óptima de líneas transmisión (OTS) (, ; , ; , ; , ) ante eventos de contingencia ( , ; , ; , ; , ),lo cual permita apreciar sus efectos en la cargabilidad de las líneas de transmisión y en la estabilidad del SEP (, ; , ) minimizando costos de operación.
Cabe indicar que la OTS es una metodología que permite aliviar el estrés operativo de ciertos elementos de un SEP, bajo ciertas con- sideraciones de funcionamiento del sistema, las LT son desconectadas para redirigir un flujo de potencia en exceso (, ; , ; , ; , ; , ).
OTS fue desarrollada como una solución para aliviar la congestión de los sistemas de potencia y la subutilización de los elementos ante escenarios de baja demanda (, ). Los eventos de contingencias son considerados para la planificación operativa en (, ) en donde se aplica OTS para forzar el camino de los flujos de potencia y para la restauración de la operación posterior a contingencias en (, ) se aplica OTS hibridado con el índice contingencias para determinar el orden de reincorporación de los elementos del SEP.
La planificación de los SEP ha sido muy poco abordada empleando OTS, la mayoría de los estudios se enfoca en la robustez de los algoritmos desarrollados en base a OPF AC y DC, y a modelación del SEP posterior a la conmutación de líneas (, ; , ).
En el presente estudio, se contempla la definición de cargabilidad y máxima capacidad de las líneas de transmisión ( , ; , ), lo cual permitirá definir los límites de potencia transmisión de una línea (, ; , ; , ), para que en base a ello se formule las propuestas de expansión de los sistemas de potencia considerando flujos óptimos de potencia DC, siendo esto el principal aporte en comparación de la expuesto en literatura científica.
El estudio está organizado de la siguiente manera: Sección contiene la planificación de la expansión y formulación del SIL, Sección presenta la formulación del problema, Sección tiene el análisis de resultados y en la Sección se muestran las principales conclusiones de la investigación.
Planificación de la expansión
El estudio TEP puede ser desarrollado mediante la aplicación de flujos óptimos de potencia DC (OPF-DC), donde el problema se limita a la optimización lineal en el cual solo se toma en cuenta la potencia activa, ya que la afectación en el voltaje y la potencia reactiva se considera como mínima (, ; , ).
Dentro de las aplicaciones OPF-DC en los SEP, se encuentra el despacho económico, que permite equilibrar la generación y la demanda a un mínimo costo, otras aplicaciones relevantes de la OPF-DC es el análisis y estudio de la cargabilidad de líneas de transmisión, ángulos de voltaje y las pérdidas que se producen (, ; , ; , ).
2.1. Flujo de Potencia Óptimo DC (OPF-DC)
El flujo de potencia óptimo se caracteriza por el análisis del SEP, dejando de lado la potencia reactiva, que cuantifica las pérdidas y considera los voltajes de barra sean iguales 1 pu (, ; , ).
Adicionalmente, permite minimizar los costos en beneficio de los usuarios finales con un servicio eléctrico de buena calidad, en ese sentido, la función objetivo busca minimizar los costos de producción ()- (), sujeto a restricciones que condicionan las características de los generadores (), el flujo de potencia máximo de una línea de transmisión la cual se puede verificar en () y el equilibrio entre generación y demanda (), es decir:
Las pérdidas se definen con la siguiente expresión:
2.2 Planificación de la Expansión de la Transmisión(TEP)
La planificación de un sistema de potencia debe ser implementado previo a las actividades de diseño y construcción, y debe considerar procesos definidos a corto, mediano y largo plazo, tomando en cuenta que una planificación a corto plazo está relacionada con limitaciones en la operación del sistema, que deben ser solventadas para evitar inconvenientes con el abastecimiento de la demanda, mientras que la planificación a mediano plazo está relacionado con la repotenciación del SEP manteniendo un criterio de respaldo o redundancia que permita tener confiabilidad del sistema.
La planificación a largo plazo está orientada a la construcción de nuevas instalaciones en función del crecimiento proyectado de la demanda (Alhamrouni et al., 2014; Carrión et al., 2021).
La función objetivo para el TEP se define en la ecuación (7), sujeto a las restricciones expresadas en (8) y (9), las cuales están relacionadas con los costos de operación e inversión inicial.
Se puede verificar en la ecuación (), el SIL es directamente proporcional al cuadrado del voltaje de línea, e inversamente proporcional a la raíz de la división entre la inductancia, y capacitancia de la línea, se deduce que al incrementar el voltaje el nivel del SIL es mayor, por otro lado también se verifica que al incrementar el número de conductores por fase, la Z c característica se ve disminuida, por lo que el nivel del SIL también se incrementa (, ).
Adicionalmente se aplican los criterios de cargabilidad máxima de líneas de transmisión expresadas en (10), (11), (12), (13), también se consideran los límites de potencia de los generadores en (14) y el equilibrio entre la demanda y generación expresada en (15).
A continuación se describen las ecuaciones:
2.3 Conmutación Óptima de Transmisión (OTS)
La conmutación de líneas de transmisión (OTS) para la redistribución de flujos de potencia, representa una solución innovadora en la operación del SEP con el fin de evitar congestionamiento del SEP disminuyendo costos operativos (Fisher et al., 2008; Jabarnejad, 2018), lo cual permite solucionar problemas de forma
práctica y oportuna, cabe indicar que este tipo de soluciones es adaptable para escenarios de contingencia, donde se requiere reconfigurar el sistema para redistribuir los flujos de potencia, y así aumentar su confiabilidad (Lu et al., 2018; Zhang et al., 2017).
En varias publicaciones científicas relacionadas con OTS se han incrementado restricciones las cuales están relacionadas con la confiabilidad, pérdidas, congestión y estabilidad, manteniendo los criterios establecidos en OPF-DC (Abdi-Khorsand et al., 2017; Yang et al., 2015; Aazami et al., 2015; Bai et al., 2017; Li et al., 2017; Gupta et al., 2017; Carrión et al., 2021; Masache et al., 2021).
Para el presente estudio se consideran las siguientes restricciones, las cuales están relacionadas con las líneas que pueden dejar de operar al alcanzar su límite máximo de cargabilidad.
Lo indicado se expresa en las ecuaciones (16), (17), (18) y la ecuación (19) representa el máximo número de líneas conmutadas.
2.4 Cargabilidad de Líneas de Transmisión
La capacidad de líneas de transmisión está definida en el sector eléctrico, como uno de los problemas más relevantes al momento de definir la ampacidad o límite térmico ante condiciones máximas de flujo de carga en líneas de transmisión.
La planificación y la operación de un SEP se vuelven cada vez más complejas, y requiere un análisis más profundo al momento de definir la carga máxima que puede transportar una línea en escenarios de demanda máxima, evitando de esta manera que la línea sea afectada eléctrica y mecánicamente.
El aumento de la demanda y el crecimiento de fuentes de generación eléctrica y eventos de contingencia, pueden provocar que las líneas de transmisión experimenten aumento en su cargabilidad, para solventar esta problemática se puede operar el equipamiento de transmisión hasta su capacidad nominal, en lugar de estimar una capacidad que puede comprometer la estabilidad del SEP ante un escenario de máxima transmisión de flujo de potencia (Karimi et al., 2018), hay que recalcar que la capacidad de transferencia de carga de una línea de transmisión está principalmente limitada por tres factores: estabilidad, voltaje y límite térmico (Karimi et al., 2018).
Cabe señalar de acuerdo a Karimi et al. (2018) que los límites térmicos se definen no solo por problemas de confiabilidad, ya que se debe relacionar con los problemas que se pueden presentar con la seguridad de las líneas, pues esta debe mantener un rango de capacidad libre y evitar el aumento de la temperatura del conductor.
Hay una serie de factores básicos que limitan o determinan la capacidad de una línea de transmisión, varios de estos factores y la afectación en las líneas de transmisión. El voltaje es uno de factores más relevantes a tomar en cuenta al momento definir la capacidad de una línea de transmisión, la cual variará directamente como el cuadrado del voltaje y deja expresada la carga en kilovatios en términos de kV2.
Un criterio práctico o punto de referencia establecido, para definir la capacidad de una línea, es determinar el SIL (Surge Impedance Load), cuyo valor numérico tiene como característica principal, definir los límites del flujo de potencia de una línea de transmisión, el cual permitirá mantener al SEP dentro de un margen de estabilidad y operación óptima.
En ese contexto, para efecto del presente estudio se utilizará el valor de la potencia real para definir la cargabilidad de la línea, donde el requerimiento de potencia reactiva es igual a cero, a esta se la conoce como SIL o potencia natural de la línea, la cual se encuentra en función de la inductancia, capacitancia y voltaje entre fases de la línea de transmisión (Castellanos-Bustamante, 2014).
El SIL está definido mediante la siguiente ecuación:
La impedancia característica Zc se expresa de la siguiente manera:
La impedancia y la admitancia equivalen a:
Donde:
Considerando para un caso especial de una línea sin pérdidas donde la conductancia y la resistencia son igual a cero, la impedancia característica queda definida de la siguiente manera:
Se remplaza (24) y (25) en (21),
Finalmente, la potencia SIL queda definida de la siguiente manera (Castellanos-Bustamante, 2014):
Se remplaza (26) en (20),
Se puede verificar en la ecuación (27), el SIL es directamente proporcional al cuadrado del voltaje de línea, e inversamente proporcional a la raíz de la división entre la inductancia, y capacitancia de la línea, se deduce que al incrementar el voltaje el nivel del SIL es mayor, por otro lado también se verifica que al incrementar el número de conductores por fase, la Zc característica se ve disminuida, por lo que el nivel del SIL también se incrementa (Castellanos-Bustamante, 2014).
Cuando la potencia activa que circula por una línea es igual al SIL, la potencia capacitiva producida es igual a la potencia inductiva que consume la línea. Bajo este escenario la línea no inyecta potencia reactiva al sistema pero tampoco recibe (, ).
Si el flujo de potencia activa en una línea de transmisión supera el valor del SIL, la potencia reactiva consumida por la línea es mayor a la potencia reactiva generada por la misma, en estas condiciones la línea demanda potencia reactiva de las fuentes del SEP (, ).
Formulación del Problema
La planificación de la expansión de un SEP tiene como objetivo, definir el equipamiento a instalarse en un sistema eléctrico, el cual permita la operación confiable del sistema, minimizando los costos de inversión y de operación.
En la literatura relacionada, al análisis del TEP se puede evidenciar la aplicación de esta herramienta en diversos sistemas de análisis (, ; , ), como son los de 6 barras, 14 barras. Para el presente estudio se utilizará el sistema de 118 barras del IEEE el cual será objeto de análisis, y se verifica su comportamiento aplicando la TEP ante el incremento de la demanda y contingencias en el sistema.
El Algoritmo formula la expansión de un SEP aplicando OTS, basado en flujos óptimos de potencia OPF-DC. En el paso 1 se inicia el proceso, en el cual se declara el número de barras, líneas de transmisión, parámetros de conectividad, cargas y generadores con sus características.
En el paso 2, se procede con la obtención de las LT conmutadas con la aplicación de OTS y se mantiene el criterio de OPF-DC. En el paso 3, se ejecuta la TEP considerando al SIL como el máximo valor de cargabilidad de la línea transmisión, se aplica un periodo de planificación con incremento de la demanda a corto plazo de 2 años y largo plazo a 10 años.
Los datos de inductancia y capacitancia de las líneas para obtener el SIL son los definidos por la IEEE para un sistema de 118 barras, para el caso de barras conectadas a través de transformadores, estos se definen con un máximo de capacidad de 100 MVA.
En el paso 4, se muestra los resultados obtenidos por la metodología propuesta, hay que indicar que el algoritmo no toma en cuenta deslastre de carga, es decir considera la desconexión de LT y transformadores y no contempla la desconexión de generación.
Análisis de Resultados
La simulación se realizó con un procesador AMD Rysen 5 2500U with Radeon Vega Mobile Gfx 2,00 GHz, RAM 16 GB, 64 bit, para la optimización se empleó GAMS y para contrastar los resultados de flujos de potencia y costos de operación, se utilizó el programa PowerFactory DIgSILENT.
Se definió un primer caso de análisis el cual contempla la aplicación de la TEP sin considerar ninguna línea conmutada. Adicionalmente y en función de lo obtenido por el OTS, se definió un número máximo de ocho líneas o transformadores que pueden quedar fuera de servicio, cuyos escenarios fueron analizados con la TEP, y se obtuvieron diferentes resultados en relación a los costos de operación e inversión que debe realizarse en el sistema.
Los costos de operación de los 54 generadores térmicos se definieron en función de lo establecido por el IEEE para un sistema de 118 barras. Para el presente estudio se considera las curvas lineales de costo.
De igual manera, para todos los casos de estudio se definió el costo de 0,25E+06 $/km de construcción de línea, y de 1,50E+06 $ para transformador de potencia de 100 MVA, cabe indicar que estos valores se definieron en función de cotizaciones y precios de referencia que actualmente se encuentran en el mercado, esta información se ingresa al Algoritmo .
4.1. Tablas de Resultados
En la Tabla se describen los resultados obtenidos producto de la metodología aplicada, se puede verificar el número de equipos con- mutadas, y las líneas o transformadores que deben ser construidas en función del análisis de la TEP, para un periodo de planificación de 2 años con un incremento de la demanda del 2 % respecto al año cero.
De acuerdo con lo indicado en la Tabla , se puede verificar que para el caso sin líneas conmutadas para 2 años de planificación, la TEP nos proyecta la instalación de nuevos trasformadores de 100 MVA en la barras 8-5, 30-17 y 38-37. Se evidencia la necesidad de construir un nuevo circuito entre las barras 85-86 y dos circuitos adicionales entre las barras 86-87, además se puede verificar que el costo de inversión es de 49,5 M$.
En la Tabla , se describen los resultados obtenidos producto de la metodología aplicada, se puede verificar el número de equipos con- mutados, y las líneas o transformadores que deben ser construidos en función del análisis de la TEP, para un periodo de planificación de 10 años con un incremento de la demanda del 10 % respecto al año cero.
Para el caso sin conmutaciones con una planificación a 10 años, se puede verificar en la Tabla que la TEP proyecta la instalación de dos nuevos transformadores de potencia de 100 MVA entre las barras 8-5 y 38-37, de un trasformador de 100 MVA en las barras 30-17, 63-59.
Adicionalmente, se evidencia la construcción de dos nuevos circuitos entre las barras 49-66, 86-87 y de un circuito entre las barras 5-11, 26-25, 25-27, 85-86, el costo de inversión es de 135,5 M$.
El análisis planteado anteriormente es aplicable para todos los escenarios donde se utiliza la TEP, los resultados se encuentran descritos en la Tabla y . Cabe señalar que, para todos los escenarios planificados, la TEP proyecta la instalación de un nuevo circuito entre las barras 85-86 y dos circuitos en las barras 86-87, estas inversiones permiten minimizar costos de operación al facilitar el despacho del generador G39, el cual tiene un costo de operación mínino.
4.2 Resultados del Ángulo de Voltaje aplicando la TEP
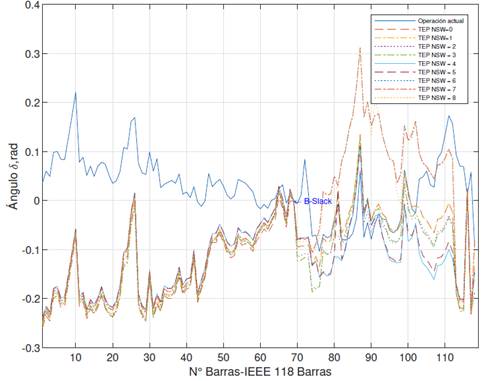
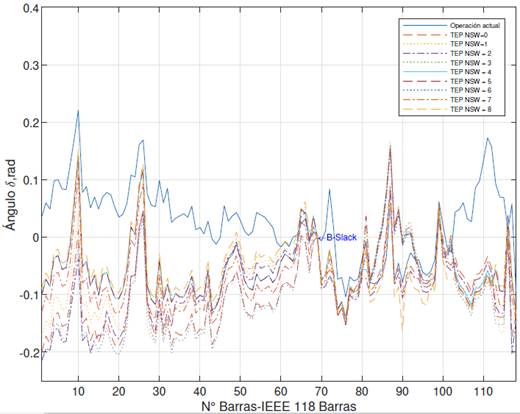
A continuación, se visualiza en las Figuras y el comportamiento del ángulo de voltaje del SEP, para los escenarios de estudio planteados para un periodo de planificación de 2 y de 10 años, respectivamente.
En la Figura se puede verificar la tendencia que mantiene el ángulo de voltaje del SEP en condiciones actuales, respecto a la tendencia del ángulo de voltaje del SEP aplicando la TEP para un periodo de planificación de 2 años, con un escenario sin conmutación de equipos y ocho escenarios con conmutación de líneas o transformadores.
Se evidencia que la tendencia del ángulo del voltaje se mantiene estable, además se verifica que el ángulo presenta fluctuaciones a partir de la barra 69 (Slack).
De igual manera, en la Figura se verifica que el ángulo de voltaje del SEP, aplicando la TEP para un periodo de planificación de 10 años, se mantiene estable y se evidencia mayor fluctuación del ángulo de voltaje en las barras del sistema.
4.3. Resultados Flujos de Potencia aplicando la TEP
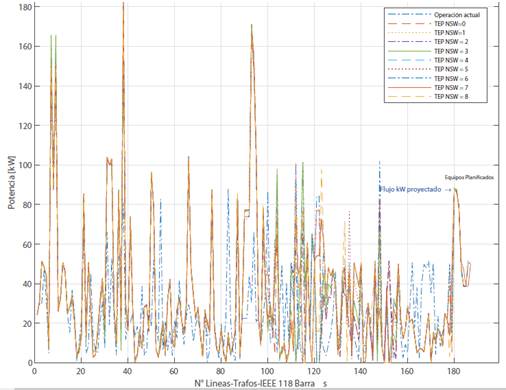
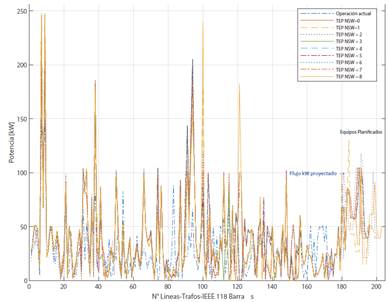
En las Figuras y , se evidencia el comportamiento del flujo de potencia en las líneas del SEP aplicando el criterio del SIL, el cual para el presente estudio define la máxima cargabilidad de la línea en condiciones ideales de operación. Estos flujos de potencia son el resultado de la aplicación de la TEP para diversos escenarios definidos en función de los equipos conmutados, considerando un periodo de planificación de 2 y de 10 años.
Cabe indicar que, en las figuras antes mencionadas, el eje x hace referencia al número de equipos tales como líneas o transformadores que conformar el Sistema de 118 Barras del IEEE.
En la Figura , se puede verificar los flujos de potencia que se obtuvieron como resultado de la aplicación de la TEP para un periodo de 2 años. Se evidencia que los flujos presentan un incremento de potencia en líneas cuyo SIL es mayor, como por ejemplo la línea que conecta las barras 26-30 que transmite un promedio de 180 MW. Se puede indicar que el SIL de dicha línea es de 324,93 MW. De igual manera ocurre con la línea que conecta las barras 38-65 que transmite un promedio de 168 MW y que tiene un SIL de 325,71 MW. Lo indicado anteriormente, también se lo puede verificar en la Figura .
En la Figura , se puede verificar los flujos de potencia de las líneas y transformadores a instalarse en el SEP para el periodo de planificación de 2 años.
En la Figura , se puede comprobar la cantidad de equipamiento a instalarse en el SEP, producto de la aplicación de la TEP para un periodo de planificación de 10 años.
4.4 Resultados de los Costos de Operación Aplicando la TEP
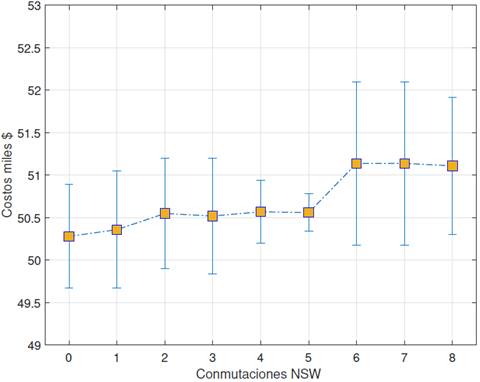
En las Figuras y , se muestran los costos de operación calculados por el programa de optimización GAMS, respecto a los costos calculados mediante el optimizador del PowerFactory DIgSILENT, se contempla para el análisis los escenarios en los cuales se aplicó la TEP para 2 y 10 años de planificación. Es necesario señalar que en las gráficas antes mencionadas se muestra la diferencia de costos de operación a través de barras de error.
En la Figura , se puede evidenciar los costos de operación para un periodo de planificación de 2 años y un incremento de la demanda de 2 % respecto al año cero. Se evidencia una tendencia uniforme de los costos hasta el escenario donde se conmuta el quinto equipa- miento (línea o transformador), a partir de esta se verifica un ligero incremento.
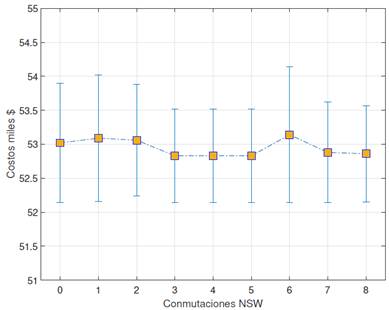
Para el periodo de planificación de 10 años (Figura ) con un incremento de la demanda de 10 % respecto al año cero, se evidencia un comportamiento más uniforme de los costos para los diferentes escenarios donde se aplicó la TEP.
Adicionalmente, se verifica que el error en los datos de los costos obtenidos entre programa GAMS respecto a los del DIgSILENT están en un promedio del 1,5 % para el periodo de planificación de 2 años y de 1,3 % para el periodo de planificación de 10 años.
CONCLUSIONES
Basándose en el análisis global, las contingencias en el SEP pueden realizarse a través del OTS, ya que la metodología permite desconectar equipamiento de la red, lo cual puede considerarse como un evento de contingencia, también puede servir como una herramienta de operación en caso de que el equipo entre en mantenimiento.
La cargabilidad de la líneas de transmisión se obtuvo a través del valor del SIL el cual se dedujo en base a las curvas obtenidas en del modelo de Saint Claire. Al tratarse el presente estudio de un análisis a través de flujos óptimos de potencia OPF-DC, el valor del SIL se define como un valor constante, el cual varía en función de las características de las líneas de transmisión (capacitancia e inductancia).
Se verifica que al aplicar la TEP en el SEP, los flujos de potencia se encuentran dentro de los rangos establecidos de cargabilidad de las líneas, que para el presente estudio está definido por un SIL ideal. Cabe indicar que lo indicado anteriormente se cumple para un escenario sin conmutaciones y con conmutaciones.
Se verifica que la aplicación de la TEP permite obtener información valiosa, sobre el comportamiento del SEP en probables escenarios de operación como pueden ser contingencias, mantenimiento o por minimización de costos por pago de peaje.
La aplicación de la TEP proporciona información importante sobre la repotenciación estratégica de nuevo equipamiento en la red, que permitirá el despacho de Centrales de Generación cuyo costo de operación sea menor.
La aplicación de la TEP permite definir los costos de operación e inversión de un sistema de Potencia considerando la variación de la demanda definida en el tiempo.
Se verifica que, al implementar el concepto del SIL para definir la cargabilidad de las líneas, este limita el flujo de potencia a través de la misma, por lo que la TEP define la instalación del nuevo equipamiento para mantener los valores del SIL. Si bien esta condición de operación es ideal, hay que considerar que de aplicarla se reduciría el costo de producción de reactivos.
Dentro del análisis de los resultados obtenidos en este estudio, se realizó una contrastación de costos de operación generados por el optimizador del GAMS versus el PowerFactory DIgSILENT, obteniendo errores que se encuentran entre 0,4 % y 1,8 %, tanto para el periodo de planificación de 2 como de 10 años.
La instalación del nuevo equipamiento en el SEP, producto de la aplicación de la TEP, para el periodo de planificación de 2 y 10 años, se debe al crecimiento de la demanda y conmutación de equipos en la red, esto como resultado de la metodología aplicada en el presente estudio.
Abreviaturas
Las abreviaturas utilizadas en el presente artículo son las siguientes: