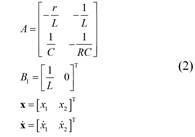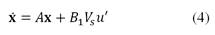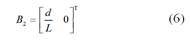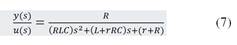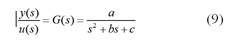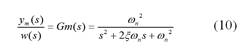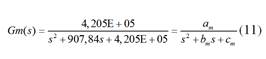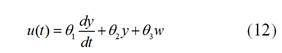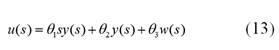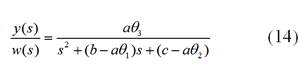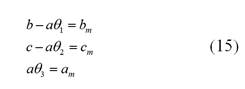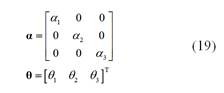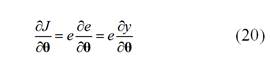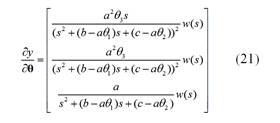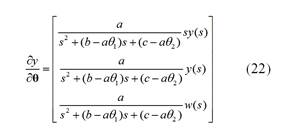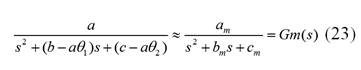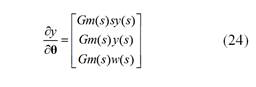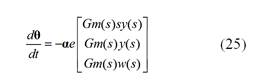Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. INTRODUCCIÓN
Los convertidores DC-DC reductores de voltaje son dispositivos ampliamente utilizados en aplicaciones en las que se requiere disminuir el voltaje de entrada y mantenerlo dentro de las especificaciones de diseño. Están presentes en cargadores de baterías, vehículos eléctricos y en aplicaciones relacionadas con energías renovables. En Roy et al. (2017) y Aliaga et al. (2019), se presenta un estudio detallado del rendimiento de convertidores reductores aplicados en el control de motores de corriente continua y sistemas fotovoltaicos, respectivamente.
El reto en el modelado y control del convertidor radica en que la dinámica de este cambia por la apertura y cierre de un conmutador, es por esto que la planta del convertidor es no lineal y discontinua. Además, la rápida dinámica del convertidor obliga a que la estrategia de control deba resolverse en intervalos de tiempo en el orden de los microsegundos.
El convertidor reductor puede funcionar en un modo de conducción continua y discontinua, y existen varias formas de representar matemáticamente la dinámica del convertidor, entre las más destacables se pueden mencionar (Erickson y Maksimović, 2020): modelo no lineal, reducido y de pequeña señal. Otros trabajos recientes proponen modelos matemáticos basados en lógica difusa (Cervantes et al., 2015). Si el convertidor funciona en conducción continua, éste se puede representar mediante el modelo matemático de pequeña señal. Dicho modelo es ampliamente usado en sistemas de control que requieren de un modelo lineal e invariante en el tiempo (Gaouzi et al., 2018), (Ardhenta et al., 2018). Este modelo posee una dinámica de segundo orden, por lo que existe la presencia de sobreimpulsos en la respuesta al escalón. Un análisis detallado en el dominio de la frecuencia del modelo promedio de pequeña señal se puede encontrar en Suskis y NiKonorov (2018).
Es común que, en un convertidor cambie el voltaje de alimentación, el voltaje de referencia y la resistencia de carga, esto representa un reto adicional para el diseño de la estrategia de control. Por lo tanto, el controlador debe lidiar con la incertidumbre de los parámetros del convertidor.
El controlador clásico proporcional, integral y derivativo (PID) ha demostrado ser eficiente en la corrección del error en estado estacionario, frente a cambios tanto en el voltaje de referencia como en la resistencia de carga (Shinde et al., 2018). Por otro lado, la respuesta dinámica depende de los parámetros de la planta, y si estos cambian, la respuesta transitoria bajo el controlador clásico PID se vuelve impredecible. Los controladores basados en lógica difusa han logrado resolver esta problemática (Swathy et al., 2018), (Patil y Jagtap, 2015), (Bendaoud et al., 2017), debido a que el diseño de estos no xpert del modelo matemático de la planta, sin embargo, se xpert del conocimiento de un xpert para plantear la base de reglas de inferencia difusa.
Los esquemas de control adaptativo directo e indirecto, han demostrado ser una buena solución al control de plantas con una dinámica cambiante en el transcurso del tiempo (Anfinsen y Aamo, 2019). Un controlador adaptativo indirecto estima los parámetros de la planta y luego modifica la estrategia de control (Andries et al., 2017). Este controlador se puede combinar con otras estrategias de control, como el control por modos deslizantes (Kannabiran y Alagarsamy, 2016) y predictivo (de León Puig et al., 2020).
El controlador adaptativo directo modifica los parámetros del controlador de tal manera que se minimiza una función de costo. Los métodos más usados para el ajuste de parámetros en el control adaptativo es la regla del MIT y la teoría de estabilidad de Lyapunov. Este último método garantiza la estabilidad del sistema, y en recientes trabajos ha sido aplicado con éxito en esquemas de control inteligente adaptativo (Nizami y Mahanta, 2016), (Khan Nizami et al., 2017). El método de ajuste de los parámetros del controlador utilizando la regla del MIT tiene la ventaja de ser un método matemático relativamente sencillo, lo cual permite evaluar sin contratiempos, la estabilidad del sistema mediante ensayos de simulación antes de su implementación.
En concreto, el aporte de este artículo es aprovechar las características del control adaptativo para regular el voltaje de salida de la planta de un convertidor DC-DC reductor de voltaje. Además, se presenta detalladamente la metodología para desarrollar un controlador adaptativo por modelo de referencia (MRAC, por sus siglas en inglés). Mediante simulación se verifica la estabilidad del control en múltiples escenarios, y finalmente la teoría se verifica mediante experimentos.
El artículo se estructura como sigue. En la sección 2 se presenta el modelado matemático del convertidor reductor. En la sección 3 se muestra la metodología del diseño del controlador MRAC. El ajuste de los parámetros del controlador se realiza mediante la regla del MIT. En la sección 4, mediante simulación numérica, se evalúa el rendimiento del controlador frente a escenarios donde cambia: el voltaje de referencia, el voltaje de alimentación, la resistencia de carga, y los parámetros de la planta en general. Finalmente, en la sección 5 se muestran los resultados del controlador funcionando en un convertidor reductor real. Las conclusiones se resumen en la sección 6.
2. MODELADO MATEMÁTICO DEL CONVERTIDOR REDUCTOR
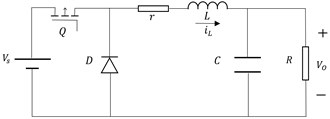
El convertidor reductor mostrado en la Figura 1 es un dispositivo conmutado de corriente continua. El voltaje de salida (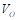
) es la variable a controlar y siempre es menor al voltaje de entrada (
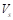). El circuito consta de un interruptor (
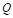), un diodo (
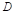), un inductor (
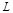) con resistencia en serie (
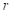), un capacitor (
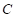) y la resistencia de carga (
).
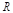Cabe recalcar que, en aplicaciones prácticas, los capacitores e inductores presentan características no ideales. En el caso del capacitor, estas características se pueden modelar mediante un resistor R c conectado en serie a dicho capacitor. Sin embargo, 𝑅 𝑐 toma valores típicos en el rango de los mili ohmios (Kimball et al., 2005), y al estar conectado en paralelo a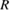 
, su efecto puede ser despreciado siempre que 𝑅≫ 𝑅 𝑐 . Por otro lado, el efecto de la resistencia parásita del inductor 
puede provocar caídas de tensión (dadas por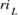 
) considerables en la carga, sobre todo para corrientes relativamente grandes.
En lo siguiente, se asumirá que 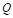, 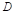y 𝐶 son ideales, y que la fuente reductora funciona en modo de conducción continua (
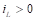). Se considera 
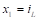y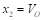 
.
2.1 Modelo no lineal
Cuando el interruptor 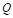cierra, 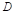se polariza en inversa, se obtiene el siguiente modelo:
Donde:
Cuando el interruptor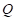 
abre,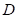 
se polariza en inversa, el sistema se puede expresar como:
El modelo no lineal conmuta entre los subsistemas de la Ecuación (1) y (3), según el estado de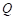 
.
2.2 Modelo no lineal reducido
A continuación, se muestra el modelo matemático no lineal del convertidor expresado en forma reducida, tomando en cuenta el modelo del convertidor con el interruptor abierto y con el interruptor cerrado de las Ecuaciones (1) y (3), respectivamente:
Donde 𝑢′ es una variable discreta adimensional, que toma únicamente dos valores: 𝑢 ′ =1 cuando 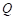permanece cerrado y 𝑢 ′ =0 cuando 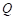se encuentra abierto.
2.3 Modelo lineal
A partir del modelo de la Ecuación (4), se puede obtener el modelo matemático lineal de la planta, o modelo promedio de pequeña señal. Para esto, es necesario tomar en consideración que el interruptor es controlado mediante modulación de ancho de pulsos. Si el ciclo de trabajo de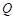 
se escribe como 
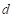, el modelo promedio se expresa como:
Donde:
2.4 Función de transferencia
A continuación, derivado de la Ecuación (5) se expresa la relación entre la salida (𝑦= 𝑉 0 ) y la entrada (𝑢=𝑑 𝑉 𝑠 ) de la
planta en el dominio complejo de la transformada de Laplace:
Como caso de estudio, los valores de los elementos del convertidor fueron tomados de tal manera que el convertidor funcione en modo de conducción continua (Erickson y Maksimović, 2020), y se muestran en la Tabla 1. La frecuencia de conmutación de 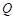se simboliza con 
.
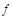Si se reemplazan los valores de la Tabla 1 en la Ecuación (7), se obtiene:
Donde 𝑎=4,058E+05, b= 251,6 y c=4,205E+05.
3. DISEÑO DEL CONTROLADOR MRAC
3.1 Modelo de referencia
Un paso preliminar al diseño del controlador adaptativo es elegir un modelo de referencia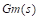 
que debe ser realizable por la planta del convertidor (Astrom y Wittenmark, 2008). Como modelo de referencia se ha escogido una planta de segundo orden (Ecuación (10)), con un factor de amortiguamiento relativo 
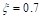y frecuencia angular natural 
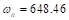rad/s:
Donde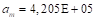 
, 
, 
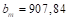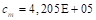y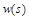 
es la entrada de referencia.
Para que la planta de la Ecuación (9) sea capaz de reproducir el modelo de la Ecuación (11), se propone el siguiente controlador:
Donde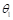 
, 
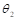y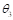 
son los parámetros del controlador que serán optimizados usando la regla del MIT, de tal manera que el sistema reproduzca el modelo de referencia. Si se reemplaza el controlador 
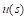en la planta de la Ecuación (9), se obtiene la siguiente función de transferencia:
Por simple inspección, al comparar las Ecuaciones (11) y (14) se puede concluir que la planta imitará perfectamente el modelo de referencia, si se cumple que:
3.1 Ley de adaptación del MIT
La ley de adaptación del MIT tiene por objetivo ajustar los parámetros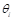 
del controlador para minimizar una función de costo 
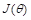(Astrom y Wittenmark, 2008). La función de costo elegida en el presente trabajo es:
Donde 𝑒 es la diferencia entre la salida de la planta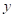 
y el modelo de referencia 
:
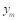La ley de adaptación del MIT para el controlador propuesto, se establece como:
Donde:
Los valores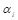 
son cantidades escalares adimensionales y positivas, que determinan la velocidad con la que se ajustan los parámetros 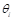. Valores relativamente pequeños de 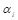provocan una convergencia lenta, valores relativamente altos pueden llevar al sistema a la inestabilidad, por lo tanto, dichos valores tienen una gran importancia en la sintonización del controlador y deben ser determinados mediante simulación usando un procedimiento de ensayo y error.
Para obtener la ley de adaptación, es necesario desarrollar la Ecuación (18):
Si se considera los resultados obtenidos en la Ecuación (14):
La Ecuación (22) no puede usarse directamente, y es necesario hacer las siguientes aproximaciones (Astrom y Wittenmark, 2008):
Se obtiene:
Finalmente, la ley de adaptación de los parámetros del controlador es:
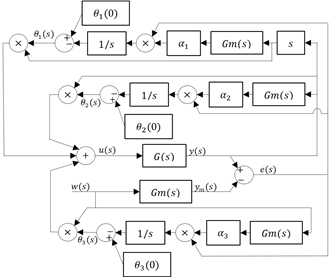
En la Figura 2 se muestra el diagrama de bloques de la planta con el controlador MRAC. Como se puede observar, se consideran los valores iniciales de los parámetros del controlador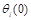 
, mismos que juegan un papel importante en
el rendimiento inicial del controlador. Los valores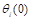 
se escogen de tal manera que se cumpla la Ecuación (15).
4. RESULTADOS DE LA SIMULACIÓN NUMÉRICA
Con el propósito de evaluar el rendimiento del controlador MRAC en condiciones cercanas a las reales, se presentan los resultados obtenidos mediante simulación de la planta de la Figura 1 usando el software Simulink. Dicha planta simulará
factores que no han sido tomados en cuenta en la fase del modelado matemático del convertidor, como: caída de voltaje en el diodo, pérdidas de conmutación y modo de conducción discontinua del convertidor. Las señales de disparo de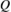 
se generan mediante una modulación de ancho de pulsos (PWM, por sus siglas en inglés) clásico, es decir, comparando 
con una portadora triangular de frecuencia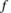 
.
Los ensayos que se enumeran a continuación son de gran utilidad para escoger los valores adecuados de las constantes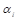 
, que como se mencionó anteriormente, son importantes para la sintonización del controlador MRAC.
4.1 Cambios tipo escalón en el voltaje de referencia
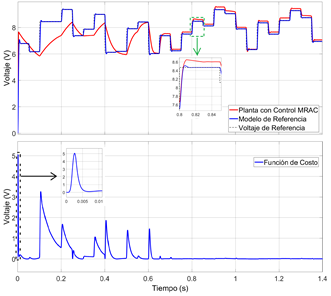
En la presente sección, se muestra la respuesta de la planta con el controlador MRAC cuando hay cambios del tipo escalón en el voltaje de referencia. Un escenario realista para esta prueba es, por ejemplo, cuando se utiliza el convertidor reductor para controlar la velocidad de un motor de corriente continua (Roy et al., 2017). En la Figura 3, se puede observar que, con el transcurso del tiempo, la respuesta de la planta con el controlador MRAC se acerca a la del modelo de referencia, y la función de costo tiende a cero.
La función de costo toma su máximo valor en el instante inicial, debido a que hay un rápido cambio de la referencia de
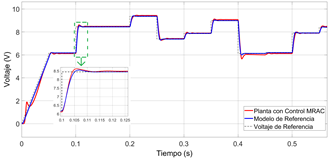
Figura 4 Respuesta a cambios tipo escalón en el voltaje de referencia con entrada inicial tipo rampa
0 a 7V. Esto provoca que los parámetros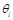 
comiencen a cambiar rápidamente, aun cuando no haya necesidad de ello.
Para evitar este efecto adverso presente en el algoritmo de adaptación, se recomienda que la entrada de referencia sea del tipo rampa hasta alcanzar el punto de trabajo, como se muestra en la Figura 4.
4.2 Cambios tipo escalón en el voltaje de alimentación
A continuación, se evaluará la capacidad del controlador para corregir el error de estado estacionario cuando cambia el voltaje de alimentación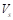 
, escenario común en aplicaciones fotovoltaicas (de León Puig et al., 2020). En el siguiente experimento numérico, se mantiene el voltaje de referencia a 6V. Inicialmente, 
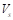es 12V cuando el tiempo de simulación 
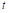es de 0,2s 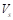cambia a 10V para volver nuevamente a 12V cuando 𝑡=0,5s.
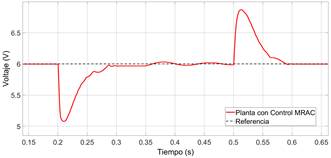
En la Figura 5, se puede observar que el controlador es capaz de corregir el error en estado estacionario, y le toma un tiempo de 0,11s llevar el error en estado estacionario a un valor menor del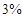 
, sin importar si el voltaje de alimentación aumenta o disminuye.
4.3 Cambios tipo escalón en la resistencia de carga
En el siguiente experimento numérico, se mantiene constante el voltaje de alimentación y referencia, y se modifica la resistencia de carga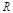 
. Un escenario real de esta prueba es cuando el convertidor funciona como fuente de alimentación y se conectan o desconectan dispositivos. Inicialmente 𝑅=5Ω, cuando 𝑡=0,15s la resistencia de carga cambia a 𝑅=10Ω, finalmente cuando 𝑡=0,25s la resistencia de carga vuelve a ser 𝑅=5Ω.
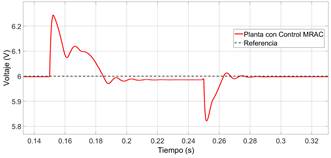
En la Figura 6, se observa que el controlador es capaz de corregir el error en estado estacionario, el mismo es llevado a un valor menor al 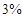en un tiempo aproximado máximo de 60 ms.
4.4 Dinámica no modelada y variabilidad en los parámetros
Finalmente, se simula la respuesta del controlador frente a dinámicas no modeladas y a variabilidad de los parámetros de la planta en general. Condiciones que están presentes en una implementación real por múltiples factores, por ejemplo, cambios de resistencia por temperatura, mala estimación en los parámetros de la planta, ruido de medición, conducción discontinua del convertidor, etc. Para esta prueba, se han aumentado los valores de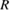 
, 
, 
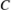y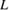 
de la Tabla 1 en un 10% respecto a sus valores iniciales. En este apartado, la respuesta del control MRAC se contrasta con un control PID clásico. Este último ha sido diseñado a partir del método de cancelación de polos y ceros, como se detalla en Medina y Naranjo (2021), tomando en cuenta el modelo con los parámetros originales y las especificaciones de diseño de la Sección 3.1, es decir, 
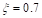y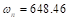 
rad/s.
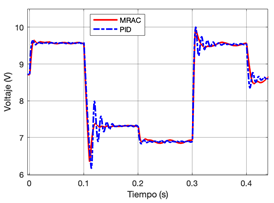
Figura 7 Comparación del controlador MRAC versus PID. a) Planta con los parámetros originales (ver Tabla 1). b) Planta con parámetros subestimados
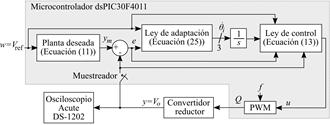
Figura 8 Esquema de la implementación práctica del sistema de control MRAC a la planta del convertidor reductor.
La respuesta de los controladores diseñados con los parámetros originales de la planta se puede observar en la Figura 7(a). Tanto el controlador MRAC como el PID tienen una respuesta transitoria y estacionaria aceptable y dentro de las especificaciones de diseño. Por otro lado, en la Figura 7(b) se observa la respuesta cuando se considera la variabilidad de los parámetros de la planta (aumentados en un 10%). En este caso, el control PID presenta un deterioro considerable en la respuesta transitoria, mientras que el controlador MRAC exhibe aproximadamente el mismo comportamiento que con la planta original.
5. RESULTADOS DE IMPLEMENTACIÓN PRÁCTICA
Con el objetivo de validar experimentalmente los resultados obtenidos en la fase de diseño y simulación, se implementó el controlador MRAC en un convertidor reductor real con las
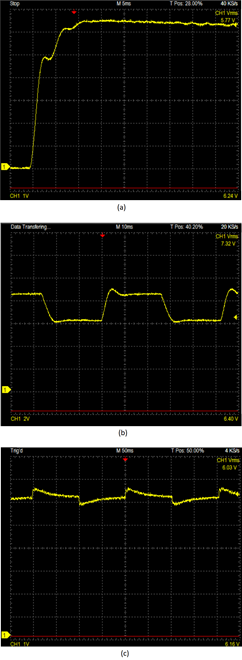
Figura 9 (a) Voltaje de salida a una entrada escalón. Escala: vertical 1V/Div; horizontal 5ms/Div. (b) Voltaje de salida frente a cambios en el voltaje de referencia. Escala: vertical 2V/Div; horizontal 10ms/Div. (c) Voltaje de salida frente a cambios de la resistencia de carga. Escala: vertical 1V/Div; horizontal 50ms/Div.
características mencionadas en la Tabla 1. El esquema de la Figura 8 resume la implementación práctica. El algoritmo de control es implementado en un microcontrolador dsPIC30F4011 funcionando a 30 mega instrucciones por segundo, con un tiempo de muestreo de 647𝜇s. Para el registro de los voltajes de salida, se utilizó el osciloscopio de computador Acute DS-1202. A continuación, se exponen los detalles de los experimentos realizados.
En la Figura 9(a), se observa la respuesta de la planta frente a una entrada de tipo escalón. El voltaje de referencia se fija a 6V. Se registra un tiempo de subida de 6,25ms, un sobreimpulso de 8,33% y un tiempo de establecimiento de 45,3ms. Luego de este tiempo, la planta alcanza la referencia. Cabe mencionar que el tiempo de establecimiento es relativamente largo debido a que los parámetros del controlador aún no han tenido tiempo para ajustarse finamente.
En la Figura 9(b), se muestra la respuesta de la planta frente a cambios de tipo escalón en el voltaje de referencia. El voltaje de referencia conmuta cada 30ms entre los valores de 6V y 8,5V. Se registra un tiempo de subida de 2,5ms, un tiempo de establecimiento de 8,13ms y un sobreimpulso del 20%. El algoritmo de control es capaz de seguir satisfactoriamente el voltaje de referencia.
La respuesta de la planta frente a cambios de carga se muestra en la Figura 9(c). El voltaje de referencia se mantiene fijo en 6V y la resistencia de carga cambia cada 100ms. En la gráfica, la resistencia inicialmente es de 𝑅=5Ω, luego cambia a 𝑅=10Ω, y el ciclo se vuelve a repetir. El error de estado estacionario toma un valor menor al 3% en un tiempo aproximado de 35ms. El controlador es capaz de corregir el error en estado estacionario cuando hay cambios en la resistencia de carga.
6. CONCLUSIONES
El controlador adaptativo aplicado a un convertidor reductor DC-DC reductor de voltaje, en múltiples escenarios, ha sido capaz de eliminar el error en estado estacionario, así como de cumplir con los requerimientos de una respuesta transitoria especificada por un modelo de referencia. Mediante la regla del MIT se ha derivado la ley de adaptación de los parámetros del controlador, y su estabilidad ha sido probada mediante simulación. Adicionalmente, presenta características superiores en la respuesta transitoria frente a un controlador PID convencional, en condiciones de dinámicas no modeladas o incertidumbre en los parámetros de la planta.
Adicionalmente, se proponen posibles temas derivados de la presente investigación con aplicación al convertidor reductor: aplicar sistemas de saturación de los integradores de la ley de control; diseñar un controlador con una planta de referencia de primer orden; desarrollar una regla de adaptación mediante teoría de estabilidad de Lyapunov, etc.
