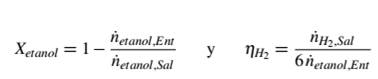1. INTRODUCCIÓN

Aproximadamente, el 80% de la demanda energética mundial es satisfecha por los combustibles fósiles, dichas fuentes de energía tienen asociadas una alta emisión de gases de efecto invernadero (fundamentalmente dióxido de carbono). Además, estas fuentes fósiles de energía están limitadas, por ser un recurso no renovable lo que implica que a futuro se presente un agotamiento de los hidrocarburos en el mundo.

En los últimos años, han surgido alternativas a partir de recursos renovables que permiten dar solución a los problemas de las fuentes de combustibles fósiles, entre las cuales se destacan las celdas fotovoltaicas, los aerogeneradores y las celdas de combustibles. Estas últimas han captado una mayor atención en términos de investigación tecnológica, siendo las celdas PEMFC (proton-exchange membrane fuel cell), las más destacadas por introducir mejoras en términos de eficiencia energética y selectividad en el transporte de los iones hidronio (H+). Estas celdas utilizan hidrógeno gaseoso como combustible, por lo que la demanda inmediata es por procesos que produzcan hidrógeno de manera limpia. Aparecen en este grupo los procesos de reformado de etanol como promisorios y de alto rendimiento, con la ventaja de disponer de etanol desde procesos fermentativo a partir de biomasa (García, 2012).

Existen diferentes estudios (García, 2012; ^{Akande et al., 2006}), que dan cuenta de la eficiencia del proceso de reformado de etanol con vapor de agua para la producción de hidrógeno molecular, el cual luego se usa como alimento para pilas de combustible. El proceso de reformado, específicamente el reformado de alcoholes con vapor de agua para la producción de hidrógeno, es un sistema complejo en el que se presentan múltiples reacciones. Particularmente, en ^{Francesconi (2008}) el reformado se hace con temperaturas de operación superiores a 503 K, siendo el metano, óxidos de carbono e hidrógeno los principales productos. La pureza final del hidrógeno que se obtiene depende de la ocurrencia o no de reacciones indeseadas, especialmente las reacciones que tengan como productos al metano, acetona y etileno, puesto que compiten con el hidrógeno molecular por el hidrógeno atómico.

En la actualidad, el proceso de reformado de etanol se lleva a cabo en reactores catalíticos de tamaño laboratorio (García, 2012). Generalmente, los catalizadores usados en el reformado de etanol consisten en un metal soportado en un óxido inorgánico. El soporte ejerce una influencia importante sobre el proceso actuando como elemento dispersante y estabilizante de las partículas metálicas del catalizador. La elección del soporte es un factor clave para una buena estabilidad del catalizador, teniendo un efecto muy fuerte sobre la actividad y la selectividad del metal (^{Fogler, 2004}). El escalado a nivel industrial de los reactores catalíticos ha sido un paso limitante, principalmente por el correcto dimensionamiento de los volúmenes del reactor, los caudales de alimento y por problemas de operación como las sobrepresiones, puntos calientes en el reactor, compactación del catalizador y obstrucciones en el reactor (Francesconi, 2008). Estos problemas se pueden solucionar contando con un modelo lo más preciso posible del proceso. Contando con el modelo, el diseño, el escalado y la operación pueden optimizarse para resolver los problemas de la catálisis.

El proceso de reformado de etanol con vapor de agua resulta particularmente difícil de modelar debido a la existencia de varios catalizadores en el reactor, así como múltiples reacciones y variables de proceso involucradas. Sin embargo, existen trabajos que ofrecen una interpretación efectiva de la cinética química, lo que es un punto de partida para abordar el modelado del reactor. ^{Cifuentes et al. (2019}) proponen un modelo no isotérmico tridimensional para un reactor de reformado de etanol de paredes catalíticas. La base para ese modelo es una simulación en CFD (computational fluid dynamics). Los autores modelan mediante diferencias finitas tres reacciones bajo diferentes condiciones de operación. Los resultados de la simulación del modelo arrojaron un rendimiento máximo de producción de hidrógeno de 80 % a una temperatura de 1150 K y una presión de 4 bar. Por su parte, en ^{Afolabi et al. (2021}) reportan el reformado de etanol usando un modelo micro-cinético validado con datos experimentales de un reformado sobre un catalizador de Ni/SiO2.

La mayoría de los modelos propuestos en la literatura para el proceso de reformado de etanol con vapor de agua en un reactor de paredes catalíticas, se ha enfocado en ecuaciones diferenciales (EDs) de segundo orden en el espacio y en el tiempo, con ajuste paramétrico desde datos experimentales (Cifuentes et al., 2019). Esa tendencia, aunque efectiva y confiable, interfiere directamente en la interpretabilidad del modelo y presenta una mayor dificultad en términos de simulación e interpretabilidad, comparada con modelos que usan EDs de primer orden. Siguiendo esa línea, el presente trabajo aborda el modelado del proceso de reformado de bioetanol para la obtención de hidrógeno, pero usando EDs de primer orden, con parámetros concentrados.

El modelo obtenido es una herramienta para diseñar, escalar y optimizar la operación del proceso. Con esto, se facilita la toma de decisiones en las aplicaciones futuras de esta tecnología para la producción de energías limpias. Este trabajo está organizado de la siguiente manera: en la Sección 2 se presenta la pre-construcción del modelo, que comprende los pasos 1 y 2 del procedimiento de modelado que se sigue (^{Alvarez, 2017}). Luego, en la Sección 3 se desarrolla la construcción del modelo (pasos 3 a 7), mientras que en la Sección 4 se finaliza la aplicación del método con la solución y validación del modelo (pasos 8 a 10). Se cierra con las conclusiones y trabajos futuros^.

2. PRE-CONSTRUCCIÓN DEL MODELO

Este es el primer bloque de desarrollo del modelo siguiendo la metodología mencionada para el modelado. Se recurre a presentar el modelo por bloques para hacer más clara su deducción^.

2.1. Descripción del proceso y objetivo de modelado

El proceso a modelar es el reformado de bioetanol con vapor de agua, del cual se obtienen hasta seis moléculas de hidrógeno ( H2) por cada molécula de etanol (C2H5OH). La reacción global del proceso (Ecuación ) implica el rompimiento de un enlace C-C, por lo cual es necesario el catalizador adecuado y la energía disponible suficiente^.

C2H5OH+3H2O → 6H2+2CO2 (1)

El proceso de reformado se lleva a cabo en un reactor monolítico de tres etapas, cilíndrico de material cerámico, al cual se alimenta etanol y agua, ambos como vapores. El reactor tiene un calentamiento externo para garantizar la temperatura de operación, lo que se logra desde el paralelepído cerámico que contiene al canal cilíndrido. Este tipo de reactores ofrecen alta área superficial en comparación con el volumen del reactor. Los canales de bajo diámetro, hacen que los recorridos radiales de transferencia de masa entre la fase gaseosa y la superficie del sólido sean muy cortos. Las paredes de los canales tienen diferentes catalizadores adheridos, dependiendo de la etapa. En el caso que se trata en este trabajo, las zonas son: i) la de entrada, donde ocurre la deshidrogenación del etanol, para lo que se usa dióxido de estaño como catalizador (SnO2), ii) la intermedia, en la que se da el reformado del acetaldehído sobre un catalizador de cobalto-hierro, y iii) la final, en la que sucede el desplazamiento con vapor de agua, usando óxidos férrico y crómico (Fe2O3 y Cr2O3, respectivamente) como catalizadores. García (2012) presenta la caracterización de los catalizadores bajo condiciones de reacción in situ, usando espectroscopía infrarroja, demostrando que las reacciones que predominan en un proceso de reformado de etanol con vapor de agua son las que se discuten en la Tabla 1. Allí también se reportan las ecuaciones cinéticas para tales reacciones^.

Tabla 1 Reacciones involucradas en el proceso de reformado de etanol¹ 

El objetivo del modelo es representar los cambios de las concentraciones de todas las especies involucradas en las reacciones químicas, a medida que fluyen por los canales del reactor en dirección axial. También se deben predecir los cambios de temperatura, tanto del sólido como del gas. Estos cambios se dan en respuesta a los cambios en las condiciones operacionales del proceso.

2.3 Definición de los Sistemas de Proceso

El reactor monolítico de reformado de bioetanol tiene etapas físicas diferenciadas: tres secciones con diferentes catalizadores depositados en la pared interior del canal. Eso sugiere una partición inmediata en tres sistemas de proceso. Pero como el modelo hace el seguimiento de las variables durante todo el recorrido de la sustancia por el reactor, se realizan particiones virtuales más finas en el sentido axial. En cada una de esas particiones virtuales se consideran dos sistemas de proceso que incluyen todas las fases involucradas. En la Figura 1, se muestran las corrientes de entrada y salida al canal del reactor, así como los dos sistemas de proceso. Eso se ilustra para dos particiones contiguas i-1 e i, en la etapa intermedia, aclarando que se toma el mismo tipo de particiones para las otras dos etapas.

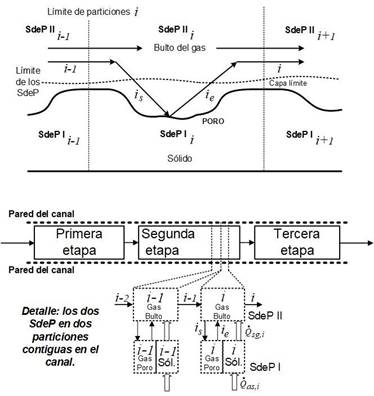
Figura 1 Sistemas de proceso tomados para el desarrollo del modelo. Las flechas gruesas indican intercambio de energía y las flechas delgadas corresponden a flujos de masa 

Los dos sistemas de proceso que se consideran para la construcción del modelo son los siguientes:

• Sistema de proceso I (SdeP I). Está formado por el sólido y volumen de gas en los poros del catalizador. El sólido es todo el material cerámico del que está compuesto el monolito. El gas es el que ocupa los espacios vacíos en el catalizador depositado sobre la cara interna de cada canal. Es en estos poros del catalizador adherido en la cara interna del canal, donde ocurren las reacciones químicas. Como esa masa de gas es despreciable comparada con la masa del sólido, se asume que todo el intercambio de calor se da solo con el sólido. Esto implica que el gas contenido en este SdeP I está a la misma temperatura que el sólido, puesto que alcanza instantáneamente el equilibrio térmico con el sólido.

• Sistema de proceso II (SdeP II). Lo forma la fase gaseosa del flujo en bulto del reactor o corriente principal de gas que viaja por el canal. Esta fase muestra el flujo continuo de materia entre la entrada y la salida total del reactor. En ella cambian las composiciones de los compuestos a medida que ocurren las reacciones químicas en el SdeP I, mediante la transferencia de masa de reactivos a la superficie del catalizador y de productos desde esa superficie al bulto del gas.

3. CONSTRUCCIÓN DEL MODELO

Este es el segundo bloque del método para obtener un MSBF. En este bloque se obtienen las ecuaciones del modelo.

3.4. Ecuaciones constitutivas y de valoración

Para cada uno de los parámetros estructurales, se debe tener una ecuación constitutiva o de valoración que permite hallar su valor numérico (^{Perez et al., 2019}). En la Tabla 2, se presentan estas ecuaciones. Es importante mencionar la relación entre las velocidades de transferencia de masa y de reacción química. Cuando la velocidad de la reacción química es mayor que la velocidad de transferencia de masa, se dice que la etapa limitante del proceso es el movimiento de las moléculas al sitio activo del catalizador (donde ocurre la reacción). La lentitud de la transferencia de masa se puede deber a: i) resistencia interna por la dificultad de las moléculas para viajar desde la superficie del catalizador al sitio activo y ii) resistencia externa por la baja difusividad en la capa límite que se forma sobre el catalizador. Siempre se considera que, por la turbulencia de la corriente de gas, la transferencia de masa de los reactivos y productos entre el bulto del gas y la capa límite es muy rápida. Por lo dicho, el modelo propuesto evalúa cuál es la etapa limitante del proceso de reformado, pues como se evidencia en la Figura 1, se da transferencia de masa en el transporte de reactivo hacia la interface y luego de productos al bulto de gas. La etapa limitante que se determine, es la que indica los flujos reales de masa de esas corrientes del proceso.

Tabla 2 Ecuaciones constitutivas y de valoración del modelo 

4. SOLUCIÓN Y VALIDACIÓN DEL MODELO

Esta es la parte final del modelado, según la metodología que se sigue para obtener modelos semifísicos de base fenomenológica (MSBF).

5. RESULTADOS Y DISCUSIÓN

Tras tener identificados todos los parámetros del modelo, se procedió a resolverlos para el arranque del reactor, asumiendo que todo está lleno de etanol y agua, con fracciones molares iniciales de 0,14 y 0,86 respectivamente. A continuación se muestran los resultados de simulación, destacando que para usar los datos experimentales reportados para la validación del modelo, se mantuvo la temperatura constante para cada etapa así: 648 K para la etapa 1, 673 K para la segunda, y 633 K para la última. Se asume equilibrio térmico entre el monolito cerámico-catalizador y el gas contenido en los poros de este último.

Tabla 3 Parámetros de entrada al simulador  

Figura 2 Resultados fracción molar de hidrógeno a las condiciones de la Tabla 3  

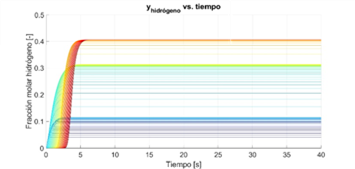
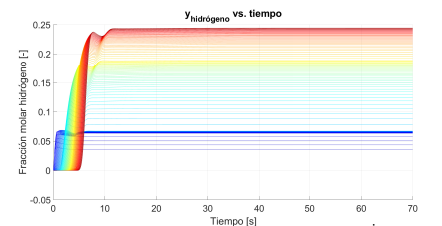
La Figura 2 muestra la evolución temporal de la fracción molar de hidrógeno (producto), en cada una de las 100 particiones del reactor. Se inicia con la ya mencionada condición de equilibrio: reactor lleno de etanol y agua, ambos como vapor. En la figura, las tonalidades de las curvas representan: primera etapa del reactor en las azules oscuras, la segunda etapa en azul claro y verde, y la tercera etapa en las amarillas y rojas. En la Figura (2) que representa a las curvas del hidrógeno, allí, los lugares donde se encuentran más separadas las curvas corresponden a cambios de etapa, puesto que cada una opera a diferente temperatura. Para mantener consistencia con los datos experimentales disponibles, no se hizo transición suave de temperatura entre etapas. La diferencia entre las fracciones molares de equilibrio de etanol rodaja a rodaja, es relativamente constante en las etapas donde el etanol es reactivo. En cambio, se observa un agrupamiento alto en las últimas rodajas, donde el etanol pasa a ser un inerte en términos de la reactividad en la tercera etapa. Este comportamiento contrasta con el del reactivo (hidrógeno), para el cual se aprecian separaciones amplias entre las fracciones de equilibrio en varias rodajas. Tal separación se debe a que el hidrógeno está presente como producto en las tres etapas del reactor, con coeficientes estequiométricos distintos.

Para contrastar el desempeño del modelo con los datos experimentales, se define la conversión Xetanol y el rendimiento ηH2 de reacción. El primero indica el grado de cambio del reactivo límite y el segundo que tan eficiente es la producción del compuesto de interés, en este caso el hidrógeno.

(18)

Con los subíndices Ent y Sal para indicar entrada y salida de una partición, los resultados obtenidos para estos dos índices a partir de la simulación del modelo propuesto fueron de Xetanol=92,22 % y de ηH2=94,87 %. Contrastando estos resultados con los datos presentados en ^{García et al. (2009}), que reportan valores de Xetanol=90,47 % y ηH2=96,35 % respectivamente, se aprecia que para ambos valores las predicción del modelo tienen errores menores al 5%.

Una de las ventajas del modelo que se propone es que representa muy bien la situación de no equilibrio térmico entre la mezcla gaseosa y el monolito cerámico-catalizador. Eso permite simular el reformado de etanol en tres etapas con variación de temperaturas en la superficie del monolito-catalizador, con su efecto sobre la fase gaseosa. Eso implica la existencia de una acción de control, aquí tomada constante, que entrega calor desde el exterior del reactor. Para esto, los parámetros adicionales usados en el modelo son: i) coeficiente global de transferencia de calor entre el monolito y la mezcla gaseosa de U=1.000Wm2 K y ii) conductividad térmica de la fase sólida (monolito-catalizador) de k=0,8Wm K.

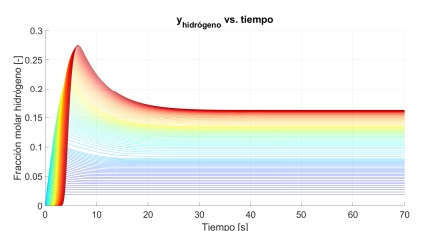
En la Figura 3, se muestra el efecto que ejerce el ingreso de más o menos calor, para mantener una temperatura diferente en cada etapa del reactor. Como se observa, se reduce la conversión de etanol, pues a la salida del reactor el etanol tiene una fracción molar superior a 0,06. Esto contrasta con lo evidenciado en el comportamiento adiabático pues la fracción final de etanol a la salida del reactor está por debajo de 0,01. Este efecto se debe principalmente a que la reacción de la primera etapa del reactor, donde se consume etanol, es endotérmica, y por tanto, al disminuir en este ensayo la temperatura de la etapa, se disminuye también la velocidad de reacción. Del mismo modo, este fenómeno explica la baja producción de hidrógeno evidenciada en la Figura 3, cuando se compara con los resultados de la Figura 2.

En la Figura 4, se muestra el comportamiento de las temperaturas de la interfase sólido-gas y del seno del gas, entre dos estados estacionarios en todo el reactor en operación adiabática. En esta condición, no entra ni sale calor del reactor. Por lo tanto, la energía requerida o liberada en cada etapa afectará la temperatura del sólido y del gas. Es importante denotar que estas curvas corresponden a los valores esperados para operación adiabática, recordando que las dos primeras etapas del reactor tienen reacciones endotérmicas, lo que hace que las temperaturas del sólido y de la mezcla gaseosa bajen drásticamente. Se destaca, además, la similitud en las dos respuestas, mostrando que el equilibrio térmico entre el gas y el sólido se alcanza muy rápido.

Para contrastar con la operación adiabática, en las Figuras 5 y 6, temperaturas, la concentración de reactivo y de producto, respectivamente, cuando se usa un flujo de calor constante desde el horno exterior al reactor de Q˙h=227 W. Los cambios en los perfiles de concentración de los compuestos debido al efecto del flujo de calor proveniente del horno evidencian la necesidad de controlar una a una las etapas, puesto que la temperatura de cada una de ellas es crítica para lograr los objetivos del reactor como un todo. En los resultados se observa como la producción de hidrógeno y la conversión de etanol disminuyen al operar bajo la condición adiabática (sin entrada o salida de calor del exterior). Cuando se adiciona calor desde el horno exterior, las etapas con reacciones endotérmicas se ven favorecidas. En contraposición a esta estrategia se observa como las temperaturas de los sistemas de proceso SdeP I y SdeP II se inestabilizan y se alcanzan valores no deseados pues para estas condiciones existen reacciones secundarias, por lo cual, se evidencia la necesidad de un control de temperatura que mantenga al sistema en los rangos óptimos.

Figura 3 Resultados fracción molar de hidrógeno en operación adiabática  

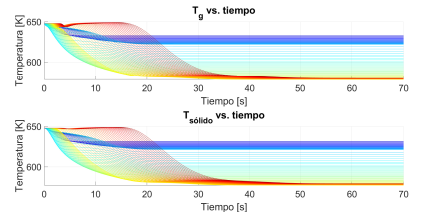
Figura 4 Dinámica de las temperaturas del sólido Tsolido´ y de la fase gasesosa Tg en operación adiabática 

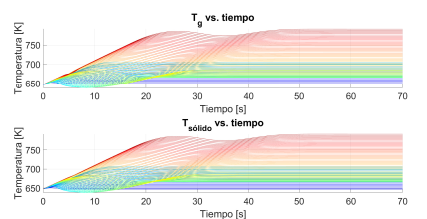
Figura 5 Dinámica de las temperaturas del sólido Tsolido y de la fase gasesosa Tg en operación Q˙h = 227 W. 3 

Figura 6 Resultados fracción molar de Hidrógeno en operación Q˙h = 227W 

Finalmente, también se validó el modelo a partir de perfiles de concentración en estado estacionario en el reactor (^{García et al., 2010}). Desde esos perfiles, se tomaron cuatro puntos a las distancias desde la entrada del reactor que se reportan en la Tabla 4. Se simuló el modelo propuesto en un tiempo suficiente para alcanzar el estado estacionario y leer las concentraciones en la partición que corresponde a las distancias mencionadas. Las tablas muestran como el modelo presenta un error muy bajo para la etapa de deshidrogenación del etanol, y errores bajos para las etapas de reformado de acetaldehído y desplazamiento con vapor de agua (Tabla 4). Se insiste en la imposibilidad de validar la respuesta dinámica, pues todo lo encontrado en la literatura son datos experimentales de estado estacionario. Sin embargo, el contrastar los valores en estado estacionario en diferentes puntos del reactor permite validar el modelo propuesto, puesto que bajo las mismas condiciones de operación, el modelo entrega valores similares de los flujos molares y temperatura al interior del monolito en cada una de las etapas, respecto de los reportados en la literatura.

Tabla 4 Comparación resultados Flujo molar de H ₂ : Etapa de deshidrogenación de etanol  

6. CONCLUSIONES Y TRABAJO A FUTURO

Del análisis de las simulaciones se evidencia que, al replicar las condiciones operativas reportadas en la literatura, el modelo predice correctamente el comportamiento dinámico de las fracciones molares de los compuestos involucrados en el proceso de reformado. Una ventaja del modelo propuesto es que está formado por ecuaciones diferenciales ordinarias, en vez de parciales, que resultan de los balances de masa y energía sobre los dos sistemas de proceso delimitados. Esto es una simplificación considerable en comparación con los modelos comúnmente usados para este proceso (pseudo homogéneos de segundo orden), reduciendo así el orden de complejidad del algoritmo para la solución del modelo y facilitando los análisis de sensibilidad de los parámetros estructurales y funcionales del mismo.

Los dos grandes aportes de este trabajo son la construcción de un modelo que tiene en cuenta las limitaciones por transporte de masa y por cinética de reacción que permite determinar las condiciones bajo las cuales la producción de un reactor monolítico puede ser las más adecuadas. Dicho modelo logra especificar si la limitación del proceso es la transferencia de masa o es la reacción química. Saber esto ayuda a implementar acciones de control más eficientes en el reactor: manipulando el flujo de gas o manipulando los flujos de calor. El segundo gran aporte es la capacidad de predecir todas las trayectorias temporales de las variables de interés para un reformador de etanol. Esto permite predecir con precisión, no solo la respuesta dinámica sino los estados estacionarios de este tipo de reactor, respetando la división inherente que marcan los tres tipos de catalizadores usados. Adicionalmente, su carácter dinámico lo hace muy útil para plantear estrategias de control basado en modelo, puesto que las simulaciones evidencian lo que la práctica con este tipo de reactores muestra: la necesidad de controlar cada etapa de forma independiente. Queda el reto de proponer estructuras de control que manejen de forma individual pero cooperativa, las tres entradas de calor: una por etapa.