1. INTRODUCCIÓN

Los convertidores electrónicos de potencia de corriente continua reductores han sido ampliamente utilizados en aplicaciones donde es necesario reducir la diferencia de potencial de entrada, y presentar a la salida, una diferencia de potencial controlada y dentro de los límites requeridos en las especificaciones de diseño. Existen varios factores que afectan la regulación del voltaje de salida, como, por ejemplo, la variación de la resistencia de carga debido al aumento de la temperatura, la conmutación de dispositivos electrónicos no ideales, entre otros (^{Hart, 2001}). Es por ello, que los convertidores reductores se han convertido en un tema de creciente estudio desde el punto de vista del control automático.

Se han propuesto varias técnicas, tanto del modelado matemático dinámico, como de algoritmos de control. El problema del modelado dinámico radica en que la estructura del controlador cambia debido a la conmutación de dispositivos electrónicos, lo que genera una dinámica no lineal del proceso. Existen múltiples formas de abordar el problema del modelado matemático, el modelo más extendido es el modelo promedio de pequeña señal o modelo lineal (^{Oliva et al., 2006}), pero también existen otros modelos como el modelo no lineal, reducido, he incluso modelos basados en lógica difusa (^{Cervantes et al., 2015}). El modelo promedio de pequeña señal presenta una dinámica de segundo orden, lo que provoca la presencia de sobreimpulsos y un gran tiempo de establecimiento de la diferencia de potencial de salida, frente a entradas del tipo escalón. Se debe destacar que la dinámica de segundo orden puede provocar que el convertidor opere en forma discontinua, análisis que no es abordado en la mayoría de trabajos presentados hasta la fecha.

Por otro lado, la estrategia de control debe lidiar con problemas como restricciones en la señal de control y tiempos de procesamiento muy cortos. La carga computacional del controlador debe ser resuelta en intervalos de tiempos, en general, del orden de los milisegundos (^{Liu et al., 2013}). Existen trabajos que abordan técnicas complejas de control, como el control fractal (^{Rodríguez et al., 2020}), pero que en la actualidad aún no pueden implementarse en línea. Sin embargo, el desarrollo de rápidos microprocesadores han hecho que cada vez sea mayor la factibilidad de implementar en línea técnicas de control avanzado, como el control adaptativo (Medina et al., n.d.) y el control predictivo (^{Gaouzi et al., 2018}).

El control predictivo basado en modelo ha sido una técnica de control avanzado ampliamente utilizado en la industria, y ha despertado en los últimos años un creciente interés, tanto en su desarrollo teórico como en la implementación práctica (^{Rodriguez y Cortes, 2012}). El controlador predictivo hace uso de un modelo matemático para predecir las salidas futuras de la planta, y la señal de control se obtiene de tal manera que minimiza una función de costo. En cada instante de muestreo se aplica la primera señal de control calculada y se desecha el resto, todo el procedimiento se vuelve a repetir en el siguiente instante de muestreo. Una metodología más detallada se puede encontrar en ^{Camacho y Bordons (2007}).

Para minimizar la función de costo, es común utilizar algoritmos recursivos que realizan una optimización numérica. Esto implica aumentar considerablemente el tiempo de ejecución del programa, y como consecuencia, lo vuelve imposible de aplicarse en línea por las restricciones temporales propias del convertidor reductor. Para evitar este inconveniente, la minimización de la función de costo debe ser analítica, y el horizonte de predicción lo más corto posible sin que se genere inestabilidad (^{Liu et al., 2013}). Bajo estas condiciones, el control predictivo resulta una buena solución para el problema de controlar la planta del convertidor reductor, como se puede observar en ^{Aliaga et al. (2019}), ^{Manjari y Majhi (2007}) y ^{Varaskar y Divya (2017}).

En el presente trabajo, mediante simulación, se pretende dar solución a la problemática desarrollando un controlador predictivo usando el método de matriz de control dinámica y una minimización de la función de costo analítica. Se ajustarán los parámetros del controlador predictivo para tener una respuesta temporal aceptable y asegurar el modo de conducción continua del convertidor. Para contrastar los beneficios del controlador predictivo con un controlador convencional, se propone diseñar un controlador proporcional, integral y derivativo (PID) y comparar sus respuestas temporales transitorias.

El trabajo se organiza de la siguiente manera: en la sección 2 se obtiene el modelo matemático del convertidor reductor, se diseña el controlador predictivo en la sección 3, en la sección 4 se diseña el controlador PID, los resultados obtenidos mediante simulación se presentan en la sección 5, y en la sección 6 se resumen las conclusiones del trabajo planteado.

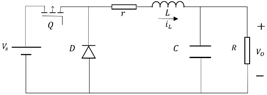
2. MODELO MATEMÁTICO DEL CONVERTIDOR REDUCTOR

El convertidor reductor de corriente continua es un dispositivo electrónico formado por un filtro pasabajos L-C en la salida, como se muestra en la Figura 1. El convertidor tiene como objetivo presentar en la salida una diferencia de potencial V0 menor que la diferencia de potencial de la entrada(Vs). El interruptor controlado(Q) se cierra de forma periódica un ciclo de trabajo d, mismo que toma valores entre 0 y 1. Cuando Q cierra, el diodo (D) se polariza en inversa y (Vs) suministra energía al filtro formado por un inductor (L) y un capacitor (C). Cuando Q se abre, el diodo se polariza en directa, y la corriente almacenada en el inductor y capacitor fluye hasta el resistor R. Debido a que los componentes no son ideales, la resistencia r representa la resistencia del inductor y la resistencia del dispositivo de conmutación Q.

Figura 1 Convertidor reductor de corriente continua  

2.3 Respuesta al escalón

En la Tabla 1 se muestran los valores de R,C, L, r, Vs usados en la simulación del convertidor. Los valores fueron calculados de tal manera que el convertidor funcione en forma continua en estado estacionario (^{Hart, 2001}).

Tabla 1 Valores de los c elementos del convertidor reductor 

Elemento	Valor
C	1,7E-03 (F)
L	1,12E-03 (H)
r	0,18 (Ω)
Vs	12 (V)
R	5 (Ω)

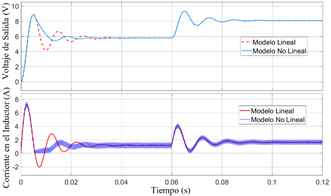
En la Figura 2, se compara la respuesta al escalón del modelo lineal y no lineal cuando la frecuencia de conmutación del interruptor es de 3 kHz. Cuando el cambio en el punto de consigna es relativamente grande, el convertidor puede llegar a funcionar en forma discontinua, debido a que la corriente en el inductor toma un valor de cero y la dinámica del sistema se comporta como la Ecuación (10). Dicho comportamiento no se ve reflejado en el modelo lineal, debido a que este modelo no tiene restricciones para corrientes en el inductor iguales o menores a cero. Cuando el cambio del punto de trabajo es relativamente pequeño, el modelo lineal y no lineal presentan respuestas idénticas.

Para el diseño de los controladores predictivo y PID se utilizará el modelo lineal del convertidor, debido a su simplicidad matemática y su buena caracterización de la dinámica del controlador cuando el convertidor funciona en forma continua.

Figura 2 Respuesta al escalón del modelo lineal y no lineal del convertidor reductor 

3. DISEÑO DEL CONTROLADOR PREDICTIVO

El método del controlador predictivo desarrollado en el presente trabajo será el método de matriz de control dinámica, DMC de ahora en adelante, propuesto por ^{Cutler y Ramaker (1980}). El rendimiento del controlador DMC depende de la calidad del modelo matemático escogido para la predicción de la planta, es por esto que en el presente trabajo se presentará un estudio detallado de la predicción de la planta. Para la obtención de la ley de control, se debe minimizar una función de costo, debe tomarse en cuenta que la minimización de la función de costo debe ser analítica, más no recursiva, es por ello que en la función de costo no se considerarán restricciones en la salida de control. Para la salida del controlador a la planta, se considera el primer valor calculado en la ley de control, y el proceso se vuelve a repetir.

4. DISEÑO DEL CONTROLADOR PID

Para el diseño del controlador PID, se tomará en cuenta la metodología de diseño basado en la cancelación de polos y ceros presentada en ^{Astrom y Hägglund (2009}) y llevada a la práctica en ^{Medina et al. (n.d.)} para convertidores reductores. Éste método se basa en el análisis del lugar geométrico de las raíces, y tiene por objetivo cancelar los polos que provocan una dinámica no deseada en la planta. El método es posible implementarlo en plantas estables de fase mínima.

Debido a que la dinámica del modelo lineal del convertidor es de segundo orden (Ecuación (15)), se propone el siguiente controlador PID en el dominio complejo s:

La función de transferencia en lazo cerrado del controlador PID en serie con la función de transferencia en la Ecuación (15) es:

Se puede observar que la planta de segundo orden se ha reducido a una planta de primer orden gracias al controlador PID, donde τ es la constante de tiempo deseada de la respuesta de la planta en lazo cerrado. Si se compara la Ecuación (34) con la ecuación canónica del controlador PID:

Se obtiene que:

Donde Kp, Ki y Kd son las constantes proporcional, integral y derivativa respectivamente del controlador PID. Para discretizar el controlador PID, mediante simulación, se ha determinado que el mejor rendimiento del controlador se alcanza con el método de discretización de Euler en adelanto para el término derivativo y Euler en atraso para el término integral. El controlador PID queda expresado en función del dominio complejo z y el tiempo de muestreo Ts:

5. RESULTADOS Y ANÁLISIS

A continuación se muestran los resultados obtenidos mediante simulación utilizando el software de MATLAB. Los controladores fueron sometidos a una señal de referencia del tipo escalón, en un principio la señal de referencia fue de 8,0 V y luego de 1,6 V.

Uno de los objetivos del presente trabajo fue obtener un controlador predictivo que pueda ser implementado en línea, por lo que, arbitrariamente se escogió el horizonte de predicción igual a cuatro, esto para disminuir la carga computacional. Los valores de la matriz G quedan como sigue:

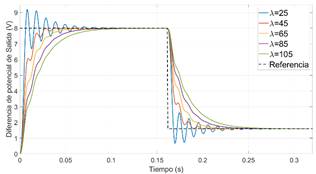
Para sintonizar el controlador MPC, se mantuvo el valor de δ=1 y se aumentó gradualmente el valor de λ. Conforme λ aumenta se penaliza la acción de control y la estabilidad relativa de la respuesta al escalón se incrementa, pero aumenta el tiempo de establecimiento, como se observa en la Figura 3. Se establece que el valor de λ=85 cumple de mejor forma el compromiso de estabilidad relativa y tiempo de respuesta.

Figura 3 Voltaje de salida según el valor de λ[/caption]  

El comportamiento de la corriente media en el inductor se observa en la Figura 4. Conforme aumenta la estabilidad relativa, la corriente en el inductor evita el funcionamiento en modo discontinuo de la fuente reductora, debido a que la corriente en el inductor se mantiene mayor a cero.

Figura 4 Corriente media en el inductor según el valor de λ[/caption]  

Para el diseño del controlador PID, se fijó como requisito de diseño una respuesta temporal sin sobreimpulsos y un tiempo de establecimiento de 20 ms. Utilizando el método descrito en la sección 3 se obtuvo los parámetros del controlador PID, que en un principio, no mostraron una respuesta al escalón favorable. Se necesitó de una sintonización fina de los parámetros, quedando finalmente como: Kp=0,245, Ki=200, Kp=1E−3.

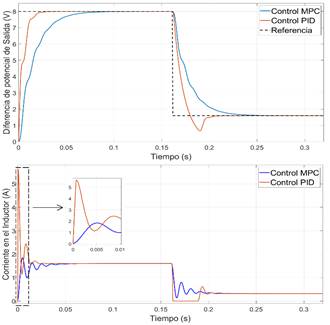
Debido a que el modelo no lineal de la planta reproduce con mayor aproximación la dinámica real de la planta respecto al modelo lineal, en la Figura 5 se presenta la respuesta temporal del modelo no lineal con los dos controladores propuestos. La frecuencia de conmutación del interruptor controlado es de f=30 kHz.

Figura 5 Respuesta del modelo no lineal con los controladores PID y MPC  

Cuando el punto de consigna es de 8,0 V, la respuesta de la diferencia de potencial de salida de la planta con el controlador PID presenta un tiempo de asentamiento de 18 ms, sin sobreimpulso. El pico de corriente en el inductor es 3,5 veces la corriente en estado estacionario, aspecto que se debe considerar para dimensionar el inductor. Cuando se da el cambio del punto de consigna a 1,6 V, el tiempo de establecimiento crece a 20 ms, y la respuesta presenta un sobreimpulso del 72%, debido a que la fuente reductora entra en modo discontinuo.

La respuesta de la planta con el controlador MPC no difiere de la obtenida con el modelo lineal, esto porque la corriente en el inductor se mantiene siempre positiva. El tiempo de establecimiento es de 53 ms sin sobreimpulso, cuando el punto de consigna es 8,0 V y 56 ms cuando es 1,6 V. El pico de corriente en el inductor es de 1,15 veces la corriente en estado estacionario.

El error en estado estacionario es cero en los dos controladores.

6. CONCLUSIONES

El modelo lineal del convertidor reductor no revela el comportamiento de la planta cuando la corriente en el inductor se reduce a cero, aspecto que se debe tener en cuenta en la fase de diseño de un controlador. El modelo lineal fue usado en la fase de diseño de los controladores MPC y PID, sin embargo, el rendimiento de éstos últimos fue evaluado con el modelo no lineal, debido a que éste refleja con mayor aproximación la dinámica real de la planta.

Para implementar el controlador MPC basado en el método de matriz de control dinámica, basta con proyectar la respuesta libre del sistema, y el horizonte de predicción puede ser seleccionado de forma arbitraria en función de reducir la carga computacional. La respuesta temporal del modelo no lineal de la planta con el controlador MPC fue capaz de seguir satisfactoriamente la trayectoria de referencia. La respuesta al escalón no posee sobreimpulso, pero en contrapartida presenta un tiempo de asentamiento mayor comparado con la respuesta de la planta bajo el controlador PID. Resulta muy sencillo sintonizar el controlador MPC, basta con aumentar gradualmente el valor de λ hasta que se cumpla con los requisitos de estabilidad relativa y tiempo de establecimiento.

El método de diseño propuesto en el presente trabajo para obtener las constantes del controlador del controlador PID, dio una primera aproximación a los valores de Kp, Ki y Kd, pero requirió de una sintonización fina de los mismos. Modificar los valores de las constantes del controlador PID requiere de cierto conocimiento de los efectos de las constantes en la respuesta transitoria, no sucede lo mismo con el controlador MPC, que presenta un método más intuitivo de sintonización.

El controlador PID presenta un menor tiempo de asentamiento, pero esto provoca picos de corriente relativamente grandes comparados con el control MPC, que deberán ser tomados en cuenta para dimensionar el inductor y el elemento de conmutación. Si el cambio del punto de consigna es relativamente grande, la fuente bajo el control PID puede funcionar en forma discontinua y generar sobreimpulsos considerables, que no pueden ser predichos en la fase de diseño utilizando el modelo lineal de la planta.

La respuesta en estado estacionario presenta un error de posición nulo en los dos casos, por lo que los dos controladores son capaces de eliminar el error en estado estacionario.