Densidad de energía libre

El análisis parte con la determinación de la densidad de energía libre de Ginzburg-Landau-Devonshire de la nanoesfera de PT, a la cual se añaden la densidad de energía de despolarización, la densidad de energía de paredes de dominio y la densidad de energía electro-elástica.

La densidad volumétrica de energía libre, FP, de un cristal ferroeléctrico en ausencia de campos eléctricos externos se expresa como serie de potencias pares de la polarización P (^{Rabe et al., 2007}):

donde α=α0T−T0∞ depende a la vez de la temperatura T de la nanoesfera y de la temperatura de transición T0∞ del PT. Allí α0, β y ζ son coeficientes cuyos valores pueden obtenerse desde experimentos, o pueden calcularse por métodos de primeros principios (^{Lallart, 2011}).

A la anterior densidad de energía se añade la densidad de energía de despolarización, Fd, debida al campo eléctrico de despolarización, la cual representa la energía eléctrica necesaria para la formación de los dominios de 180° en la nanoesfera (^{Andrade y Lascano, 2017}):

donde ϵ*=4ϵ0π3, D es el diámetro de la nanoesfera de PT, d es el grosor de cada dominio de 180°. Además, allí se considera una nanoesfera cubierta por una capa de grosor t de cargas eléctricas espaciales.

Asimismo, también debe añadirse la densidad de energía Fσ correspondiente al efecto de esfuerzos mecánicos σ aplicados sobre la nanoesfera de PT, los cuales pueden también originarse en la transición desde una fase paraeléctrica cúbica a una fase ferroeléctrica tetragonal del PT. Ya que la fase ferroeléctrica del PT es tetragonal, su polarización está determinada únicamente por la componente P3 del campo de polarización P→=0,0,P3, (^{Sun et al., 2010}), es decir, P=P3. Además, al contrario de lo realizado en el trabajo de ^{Cao y Cross (1991}), aquí se toma en cuenta la condición hidrostática para los esfuerzos mecánicos, esto es: σ1 = σ2 = σ3 = σ, σ4 = σ5 = σ6 = 0. Por lo tanto, la densidad de energía Fσ es (^{Andrade y Lascano, 2017}):

donde los Qij son los coeficientes electroestrictivos.

De este modo, sumando las Ecuaciones (1), (2) y (3), obtenemos la energía libre por unidad de volumen, notada como F1, de una nanoesfera ferroeléctrica con una estructura de dominios de 180°, su valor es:

Todos los valores de los coeficientes que intervienen en la densidad de energía F1 de la Ecuación (4) aparecen detallados en la Tabla 1.

Agrupando los términos de P 2 en la Ecuación (4) se obtiene:

Finalmente, a la anterior densidad de energía se le añade la contribución de la densidad de energía de pared de dominio, Fw, la cual depende del gradiente del campo de polarización que existe en la pared, y que representa físicamente la densidad volumétrica de energía en la dirección de mayor cambio de la polarización en el espacio, y puede expresarse así:

donde g es el coeficiente de energía del gradiente de polarización que depende de la naturaleza del cristal.

De este modo, añadiendo a la energía dada en (5) la densidad de energía de la relación (6), se obtiene la densidad de energía del sistema en estudio:

donde por facilidad de análisis se ha introducido el coeficiente

12A=12α+ϵ*tdD21−e−2πDd−Q11+2Q12σ.

Además, si se limita el estudio al caso cuasi-unidimensional en el que la variación de la polarización ocurre tan solo en dirección perpendicular a la misma, y si se denomina como eje X a aquel de la dirección de cambio de la polarización, con el origen en el centro del dominio, entonces el gradiente de la polarización se reduce a ∇P= dPdx, y la densidad volumétrica de la energía libre del sistema resulta ser:

3.1. Los estados de equilibrio

Una vez determinada la densidad de energía libre del sistema, el equilibrio estático del mismo se puede obtener aplicando el método variacional a dicha densidad de energía, el cual se expresa por:

Se puede considerar que los dominios del sistema constituyen fases homogéneas, es decir, que dentro de cada uno de ellos no hay variación de las magnitudes físicas, por lo que la Ecuación (9) se reduce a ∂F∂P=0, condición que aplicada a la Ecuación (8) equivale a:

cuyas soluciones proporcionan los valores de polarización de los estados de equilibrio de los dominios, los mismos que son:

P=0

La solución P=0 corresponde a la fase cúbica paraeléctrica del sistema, y la solución (11) describe los dos estados de polarización de la fase ferroeléctrica tetragonal, es decir que la polarización en tal fase está dada por P→=0,0,±P0. La dirección de P→ es perpendicular a la dirección X definida anteriormente. Son justamente estas dos posibilidades de orientación de la polarización, energéticamente equivalentes, las que dan lugar a la estructura de dominios de 180° y, por consiguiente, en la aparición de una pared de dominio entre dos de ellos.

La pared de dominio es una zona de transición entre los dos valores de la polarización P→ dados por la Ecuación (11), y como tal es una región heterogénea del sistema. Por ello, el perfil de la polarización en la pared de dominio se puede obtener aplicando el principio variacional (9) a la densidad de energía libre dada por la Ecuación (8), lo cual conduce a la siguiente relación:

Para la resolución de la Ecuación (12) dentro de la pared de dominio se ha realizado un procedimiento análogo a los realizados en los trabajos de ^{Cao y Cross (1991}) y de ^{Falk (1983}), involucrando el uso de integrales elípticas de tercera clase. Las condiciones de borde necesarias consisten en el hecho antes descrito de que la polarización a los costados de la pared toma los valores 0,0,±P0, las cuales además corresponden a la dirección [001]. ^{Meyer y Vanderbilt (2002}) y ^{Torres Sancho (2009}) reportan la existencia de paredes de dominio de 180° paralelas a esas mismas direcciones en el PT para su fase ferroeléctrica tetragonal. Con todo ello, se obtiene la solución siguiente:

donde:

La Expresión (13), solución de la Ecuación (12), representa el perfil de la polarización a través de la pared de dominio en la fase ferroeléctrica tetragonal de la nanoesfera, mientras que la Ecuación (14) representa el espesor de la pared de dominio de 180°. Tanto el perfil como el espesor dependen de las condiciones en la que se encuentra la nanoesfera a través de las cantidades A y P0, y es lo que se analiza a continuación.

Para obtener resultados numéricos a partir de las soluciones antes encontradas es necesario conocer el valor del coeficiente g de energía de gradiente para el PT, además de hacer uso de los valores presentados en la Tabla 1. La literatura ofrece datos provenientes indirectamente de medidas experimentales, y otros provenientes de simulaciones para sistemas de PT próximos al que se estudia en este trabajo. En el trabajo de ^{Li et al. (2001}) se dan valores experimentales de coeficientes Gij del gradiente de energía de pared de dominio, tales que para el sistema aquí en estudio, que es cuasi unidimensional, se tiene que g ≡G11=0,6G110, donde G110 es una constante para normalizar G11 durante la simulación y se relaciona con el espaciado de la cuadrícula en el espacio real (^{Choudhury et al., 2005}). Con base en medidas experimentales, ^{Li et al. (2001)} manifiestan que el valor de G110 está en el intervalo comprendido entre 0,9×10−10 y 6,8×10−10C−2m4N. Si bien ^{Shin et al. (2007}) mediante simulación en dinámica molecular han calculado coeficientes del gradiente de polarización con valores menores asociados a los planos (100), en el presente trabajo se ha decidido adoptar, en primer lugar, un valor experimental y, en segundo lugar, el valor menor del intervalo antes anotado, por cuanto este valor está relacionado con el estado de menor energía de pared de dominio y, por tanto, posiblemente el más probable; dicho valor es g=0,6×0,9×10−10C−2m4N=0,54×10−10C−2m4N y es el que se ha utilizado en los cálculos que aquí se presentan.

No se han encontrado estudios experimentales que muestren el perfil de la pared de dominio de 180° del titanato de plomo en función de la temperatura, tamaño de partícula, y la capa de cargas eléctricas libres en su superficie; y tampoco la de grosor de pared de dominio en función de los parámetros ya mencionados a escala nanométrica. Por otro lado, existen trabajos como los de los autores ^{Lee et al. (2009}), ^{Behera et al. (2011}) y ^{Pöykkö y Chadi (1999}), donde mediante cálculos de primeros principios y de DFT se obtienen perfiles de la polarización en la pared de dominio del titanato de plomo para el cuerpo masivo, de modo que su escala en cuanto al grosor es de los amstrongs, lo cual no es compatible para realizar una comparación con el modelo aquí presentado que se refiere a una escala nanométrica.

3.2. Polarización en la pared de dominio 180°

En la Figura 1 se presenta el perfil de polarización en función de la posición dentro de la pared de dominio de la nanoesfera de PbTiO3 para una polarización espontánea del cuerpo masivo igual a P0=0,75 C/m2, y obtenida a partir de la Ecuación (13). Allí se observa que la polarización cambia de signo cuando cruza el centro de la pared, como era de esperarse, y se satura en los valores P0=±0,75 C/m2. La polarización sigue el comportamiento de una función simétrica alrededor del centro de la pared de dominio.

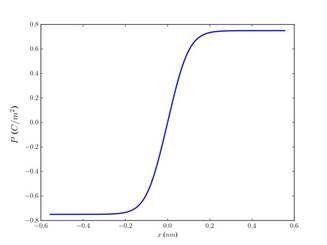
Figura 1 Polarización en función de la posición en la pared de dominio de 180°, para una polarización espontánea de cuerpo masivo P 0 = 0,75C/m2 

Los resultados que se muestran a continuación provienen de aplicar las Ecuaciones (13) ó (14) simultáneamente con la Ecuación (11). Esto se realiza por cuanto se quiere conocer el comportamiento de la polarización de la pared de dominio, o el grosor de pared de dominio, en función de parámetros tales como son la temperatura, el diámetro de la nanoesfera, el espesor de la capa cargas espaciales que cubre a la nanoesfera de PT y los esfuerzos mecánicos, todos los cuales se encuentran implícitamente en la Ecuación (11).

En la Figura 2 se presenta el perfil de la polarización en función de la posición dentro de la pared de dominio 180° para varias temperaturas del sistema. Allí se observa que, en general, la polarización decrece notablemente cuando la temperatura se incrementa; a las temperaturas de 0 K, 298,15 K y 500 K los perfiles de polarización son semejantes entre sí, no así para la temperatura de 636,67 K donde el valor de la polarización experimenta una reducción notable y el comportamiento es muy distinto al que aparece para las temperaturas antes mencionadas. Esto es, al igual de lo que sucede con la polarización espontánea en los dominios ferroeléctricos, el valor de la polarización a través de la pared de dominio se reduce drásticamente cuando la temperatura del sistema se aproxima a la de su transición ferroeléctrica.

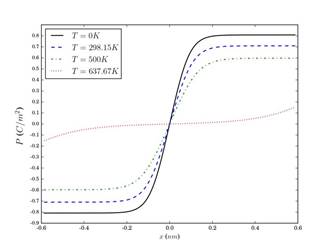
Figura 2 Polarización en función de la posición en la pared de dominio de 180° de una nanoesfera de diámetro 20 nm a diferentes temperaturas, con configuración de 3 dominios y capa de cargas libres de espesor t = 0,2 nm 

La Figura 3 presenta la polarización en función de la posición dentro de una pared de dominio 180° para una nanoesfera de PT con diferentes diámetros, un espesor fijo de la capa de cargas libres en su superficie y a temperatura ambiente. Se observa que, para todas las posiciones, al disminuir el tamaño de partícula también disminuye el valor de la polarización, y esta reducción es muy pronunciada para el valor de diámetro D=5,47 nm de la nanoesfera. Este valor de diámetro es el valor crítico calculado en el trabajo de ^{Andrade y Lascano (2017}) para la nanopartícula de PT, diámetro para el cual la polarización espontánea prácticamente se anula.

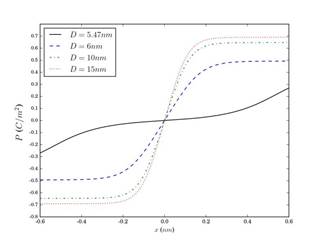
Figura 3 Polarización en función de la posición en la pared de dominio de 180°, para varios diámetros de la nanoesfera, con configuración de 3 dominios, capa de cargas libres de espesor t = 0,2 nm y a temperatura ambiente T = 298,15 K 

En la Figura 4 se presenta el perfil de la polarización en función de la posición dentro de una pared de dominio de 180° en una nanoesfera de PT de 20 nm de diámetro y a temperatura ambiente, para diferentes espesores de la capa superficial de cargas libres. El aumento del grosor de la película de cargas libres sobre la superficie de la nanopartícula reduce, para todas las posiciones, el valor de la polarización en la pared de dominio. Particularmente, para el valor de t = 0,73nm, hay una gran distorsión del perfil de la polarización respecto al perfil que se observa para el espesor t=0,20 nm, lo cual expresa la fuerte influencia de la capa de cargas libres sobre el campo de despolarización dentro de la pared de dominio.

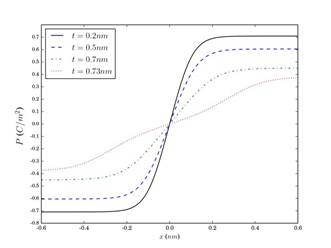
Figura 4 Polarización en función de la posición en pared de dominio de 180° de una nanoesfera de diámetro D = 20 nm, para varios grosores de capa de cargas libres superficiales, con configuración de 3 dominios y a temperatura ambiente T = 298,15 K 

La Figura 5 presenta la polarización en función de la posición en una pared de dominio 180° para una nanoesfera de PT con 100 nm de diámetro y a 50 K de temperatura, para diferentes valores de esfuerzos mecánicos aplicados sobre la misma. Se observa que los esfuerzos de tensión (esfuerzos positivos) hacen que el perfil de polarización aumente ligeramente en relación con el perfil de polarización en ausencia de esfuerzos (línea negra). En contraste, bajo la presencia de esfuerzos de compresión (esfuerzos negativos) el perfil de polarización en la pared de dominio se reduce significativamente respecto al caso de la nanoesfera libre de esfuerzos; tal reducción es mayor a medida que los esfuerzos de compresión aumentan, y podría suceder que para valores elevados de esfuerzos de compresión se altere la estabilidad ferroeléctrica del sistema. Puede sugerirse que, a escala nanométrica, la aplicación de esfuerzos de compresión elevados provoca una reducción del tamaño de la nanoesfera ferroeléctrica, y con ello una amplificación del efecto de tamaño de partícula ya observado en el trabajo de ^{Andrade y Lascano (2017}).

3.3. Espesor de pared de dominio de 180°

En la Figura 6 se representa el espesor de la pared de dominio en función de la polarización espontánea de la nanoesfera de PT. Allí se observa que el espesor de pared de dominio se incrementa de manera abrupta cuando la polarización espontánea se acerca su valor crítico dado por PT=TC−= −β2ζ=3,053×10−1C/m2 y calculado en el trabajo de ^{Andrade y Lascano (2017}) para la nanoesfera de titanato de plomo. Aparece así un resultado peculiar: un crecimiento brusco del espesor de la pared de dominio cuando la partícula se acerca a la transición ferroeléctrica. Una posible interpretación es que este acelerado crecimiento del grosor de pared de dominio hace que la pared de dominio vaya ocupando más volumen dentro de la nanoesfera hasta cubrir todo el cristal, cuando éste se acerca a la transición ferroeléctrica. Por otro lado, para valores de polarización superiores al crítico PT=TC−= −β2ζ=3,053×10−1C/m2, el grosor de pared de dominio se reduce notablemente y tiende a cero.

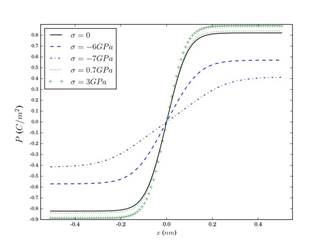
Figura 5 Polarización en función de la posición en pared de dominio 180° para diferentes esfuerzos mecánicos aplicados a una nanoesfera de PT con diámetro D = 100 nm, con capa de cargas superficiales de grosor t = 0,2 nm, con configuración de 3 dominios y a la temperatura T = 50 K 

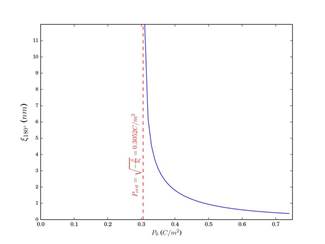
Figura 6 Espesor de la pared de dominio en función de la polarización espontánea de una nanoesfera de titanato de plomo 

La Figura 7 presenta el espesor de la pared de dominio de una nanoesfera de PT en función de la temperatura y para diferentes diámetros de la nanopartícula. Se observa que, para un diámetro definido, el espesor crece con el aumento de la temperatura y lo hace de manera muy abrupta cuando la temperatura se acerca a cierto valor, el cual es diferente para cada diámetro de la partícula. Tal temperatura es la de Curie de la transición ferroeléctrica calculada en el trabajo de ^{Andrade y Lascano (2017}), y se ve que la misma se reduce con la disminución del tamaño de partícula, lo cual concuerda con el análisis que se realiza en el trabajo mencionado. Además, se observa que a 0 K de temperatura y para todos los diámetros de la partícula, el grosor de la pared de dominio es cercano a los 0,3 nm.

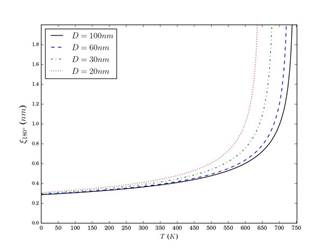
Figura 7 Espesor de la pared de dominio de nanoesfera de titanato de plomo en función de la temperatura, para diferentes diámetros de la nanoesfera, con capa de cargas superficiales de grosor de t = 0,2 nm y con configuración de 3 dominios 

En la Figura 8 se presenta el espesor de la pared de dominio en función de la temperatura de la nanoesfera de PT con 20 nm de diámetro y configuración de 3 dominios, para distintos valores del espesor de la capa superficial de cargas libres. Como era de esperarse, se observa el mismo aumento brusco del espesor cuando crece la temperatura; el valor de temperatura para el cual el incremento es súbito es aquel de la transición ferroeléctrica; tal valor se reduce de manera notable con el aumento del espesor de la capa de cargas libres superficiales, reduciéndose así la estabilidad de la fase ferroeléctrica. Además, a la temperatura de 0 K, el valor del grosor de la pared crece con el aumento del espesor de la capa de cargas superficiales.

La Figura 9 muestra el espesor de la pared de dominio en función de la temperatura de una nanoesfera de PT con 100 nm de diámetro y para diferentes esfuerzos aplicados. Se han considerado 3 dominios en la nanoesfera y una capa de cargas libres superficiales con 0,2 nm de espesor. En general, se observa el mismo comportamiento de los dos casos anteriores en relación con el aumento de la temperatura. Y además se observa que los esfuerzos de tensión aplicados provocan un incremento de la temperatura de transición ferroeléctrica y, por el contrario, los esfuerzos de compresión reducen tal temperatura. Por otro lado, para la temperatura de 0 K el valor del grosor de pared de dominio crece con el aumento de la magnitud de los esfuerzos de compresión, y prácticamente no se altera con los esfuerzos de tensión.

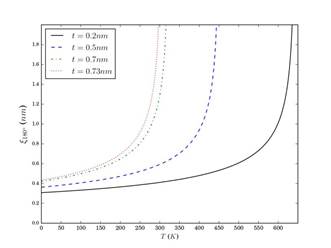
Figura 8 Espesor de la pared de dominio en función de la temperatura de nanoesfera de titanato de plomo con diámetro D = 20 nm y configuración de 3 dominios, para diferentes grosores t de la capa de cargas superficiales 

Figura 9 Espesor de la pared de dominio en función de la temperatura de nanoesfera de titanato de plomo de diámetro D = 100 nm, para diferentes esfuerzos mecánicos σ aplicados a la nanoesfera, con configuración de 3 dominios y capa de cargas superficiales de espesor t = 0,2 nm