1. INTRODUCCIÓN

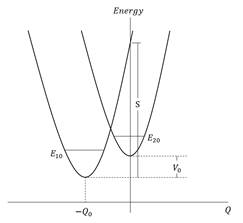
El modelo de dos estados para la descripción de los átomos y moléculas que interactúan con un campo electromagnético clásico ha demostrado ser útil en la óptica no lineal. En una molécula, tales estados son generalmente pensados como estados vibracionales que pertenecen a una o dos superficies de energías potenciales. En este trabajo, consideramos sólo el segundo caso, pero tenemos en cuenta la posibilidad de un acoplamiento intramolecular directo de estado a estado. Este tipo de modelo que consiste en dos curvas electrónicas, ya sea degeneradas o no degeneradas para una pequeña región de valor de coordenadas nucleares, se ha aplicado al tratamiento de los efectos Jahn-Teller y pseudo-Jahn-Teller en las moléculas (^{García-Sucre y col., 1970}; ^{Slivnev y col.,2020}) y al acoplamiento vibrónico que se produce para los estados excitados degenerados de los dímeros (^{Witkowsky y col., 1960}). Nuestro modelo consiste en dos estados electrónicos cuyas curvas de energía potencial se describen como osciladores armónicos desplazados en energía y coordenada nuclear. Consideramos la presencia de estados electrónicos moleculares con momentos dipolares permanentes no nulos. Nuestro sistema efectivo de dos niveles de estados vibratorios se describe en la Figura 1.

Figura 1 Representación diabática. Los mínimos de los dos potenciales están desplazados verticalmente en energía por V0 y horizontalmente por la distancia Q0. 

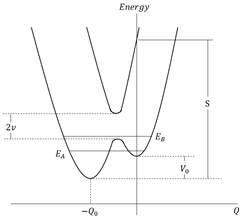
Esta descripción de los estados electrónicos entrecruzados corresponde a la llamada representación diabática. También se puede incluir una perturbación residual H˜, acoplando estos estados electrónicos. Las curvas anteriores pueden separarse según la regla de cruce evitado (Figura 2).

Figura. 2 Representación adiabática. La perturbación residual que da lugar a la separación de las dos curvas armónicas se representa de acuerdo con una regla de cruce evitado. 

Estos dos nuevos estados EA, EB del Hamiltoniano electrónico pertenecen ahora a la llamada representación adiabática y su forma depende del valor del elemento matriz no diagonal de H˜; EA y EB denotan las energías vibrónicas resultantes después de la inclusión del acoplamiento H˜. El acoplamiento intramolecular es una herramienta fundamental para explicar las transiciones entre los estados electrónicos en los espectros de absorción y emisión que se suponía que estaban prohibidas por la simetría. Las descripciones teóricas de los procesos foto-físicos y fotoquímicos en la literatura implican el tratamiento de dos o más interacciones electrónico-vibracionales (^{Thoss y col., 2000}). El acoplamiento vibrónico, resultante del acoplamiento entre los movimientos nucleares y electrónicos en una molécula es de gran importancia para algunos procesos físico-químicos, por ejemplo, en el estudio de las tasas de relajación de la conversión interna (^{Mebel y col., 1997}), en el estudio de las probabilidades de transición débiles prohibidas por la simetría en los procesos de absorción y emisión, en la espectroscopia de femtosegundos (^{Domcke y Stock, 1997}), en el estudio de la forma de la banda de absorción óptica de los dímeros (^{Pakhomov y col., 1995}) y en el estudio de las resonancias en los procesos de dispersión (^{Charutz y col., 1997}).

Nuestro sistema molecular ahora queda representado por un sistema de dos niveles no convencional, en el sentido que se lo describe en términos del acoplamiento intramolecular a través de sus estados adiabáticos. Considerando ahora este nuevo esquema, la dinámica temporal de este sistema en presencia de un baño térmico e interactuando con los campos electromagnéticos clásicos, se trata a través de las ecuaciones ópticas convencionales de Bloch, haciendo uso del formalismo de la matriz de densidad y de la ecuación de Liouville y Von Newmann. En este trabajo, proponemos una extensión de las ecuaciones ópticas convencionales de Bloch para sistemas complejos en presencia de acoplamientos intramoleculares.

2.1. REPRESENTACIÓN DIABÁTICA

La inclusión de la interacción entre el movimiento nuclear y electrónico en el cálculo de los valores y vectores propios del sistema molecular a través de HTΨTr,Q=ETΨTr,Q requiere, según la formulación general del modelo de acoplamiento intramolecular de Herzberg y Teller, poder expresar las funciones de onda electrónicas con una dependencia paramétrica en el espacio de las coordenadas nucleares Q . Estrictamente el término acoplamiento intramolecular se refiere a la corrección de las funciones de onda electrónicas de Born-Oppenheimer ΨTr,Q=ψrχQ a fin de obtener información sobre la interacción entre los movimientos electrónicos y nucleares del sistema (^{Zhao y col., 2020}). Con este fin, el término de acoplamiento Ur,Q se desarrolla en serie de Taylor para los pequeños movimientos del núcleo alrededor de la configuración de referencia previamente elegida Q0. Para simplificar, obtenemos Ur,Q=Ur,Q0+ΔUr,Q. En esta representación, las coordenadas nucleares (en el espacio) se consideran fijas, introducidas en la función de onda Ψk como parámetro. El movimiento de los electrones se obtiene con: Helect+Ur,Qψkr,Q=εkψkr,Q. Ahora, la función de onda total se desarrolla como Ψr,Q=∑kχkQψkr,Q, dondeχkQ es una función de onda vibracional en la representación diabática, calculada según

TNQ+εQχkQ+∑kWknQχnQ =ETχkQ, donde Wkn es el operador de acoplamiento no diabático.

2.2. REPRESENTACIÓN ADIABÁTICA

La función de onda electrónica se encuentra para una configuración nuclear específica Q0 que no necesariamente se refiere a la posición real del núcleo en el espacio, dada por Helect+Ur,Q0ψi0r,Q0=εkψi0r,Q0, donde ψi0r,Q0 son las funciones de onda electrónica diabáticas. La función de onda total, es Ψr,Q=∑iχi0Qψi0r,Q0 y finalmente, 

donde ψjr,Q|ΔUr,Q|ψkr,Q genera la superficie de energía potencial adiabática de los núcleos en el campo generado por los electrones. Por lo tanto, el valor de los elementos ∑k≠jψjr,Q|ΔUr,Q|ψkr,QχkQ =0 mide el efecto del acoplamiento intramolecular (^{Mita y col., 2020}). Finalmente, utilizando la teoría de perturbaciones de Rayleigh-Schrödinger, se obtiene la función de onda electrónica corregida:   

donde:

CijQ=ψi0r,Q0|ΔUr,Q|ψj0r,Q0εj0+εi0+∑k≠jψi0r,Q0|ΔUr,Q|ψk0r,Q0ψk0r,Q0|ΔUr,Q|ψj0r,Q0εj0−εi0εj0−εk0+…

Las condiciones para el cruce de dos curvas de potencial adiabático de la misma simetría en un modelo de acoplamiento de dos estados, requiere ΔUiir,Q=ΔUjjr,Q y ΔUijr,Q=0. El cruce de superficies de energía potencial se asocia con los problemas de Jahn-Teller, donde las simetrías de estado generan intersecciones cónicas. La inestabilidad de algunas configuraciones nucleares produce una distorsión instantánea de su estructura que elimina la degeneración.

3. MODELO DE ACOPLAMIENTO INTRAMOLECULAR    

El Hamiltoniano asociado al sistema molecular en presencia de acoplamiento intramolecular se define como H=H0+H˜r, donde H0 representa los dos osciladores armónicos desacoplados entre sí (sistema molecular de dos niveles con estados vibracionales sin acoplamiento intramolecular), y H˜r corresponde a un término residual de perturbación (dependiendo sólo de las coordenadas electrónicas) que induce el acoplamiento intramolecular. Las funciones propias de H0 son ψ1 y ψ2, donde y H0ψ2=E2kψ2, con estados electrónicos 1, 2 y estados vibracionales j,k. Para la inclusión de H˜r en el Hamiltoniano total, tenemos HψA=EAψA y HψB=EBψB. En la aproximación de Born-Oppenheimer ψA=χ1j ψ1 y ψB=χ2k ψ2. El acoplamiento intramolecular está representado por los elementos no diagonales del operador residual:

donde v=ψ1|H˜|ψ2, con v como el coeficiente o parámetro de acoplamiento y χ1j|χ2k la integral de solapamiento de los estados vibracionales. Los valores de energía y las correspondientes funciones propias pueden ser escritas de la forma:   

donde r y Q corresponden a las coordenadas electrónicas y nucleares, respectivamente, y donde se encuentran las siguientes cantidades:

E1j=j+12ℏω0,  E2k=k+12ℏω0+V0;  C1jA=1+AjkA−1/2, C1jB=1+AjkB−1/2con AjkA=E1j−EAv χ1j|χ2k y AjkB=E1j−EBv χ1j|χ2k.

Normalmente en los cálculos se utilizan algunos criterios que definen la intensidad de acoplamiento: débil v≪Sℏω04, intermedio v≈Sℏω04 y fuerte v≫Sℏω04, donde S=mω0/ℏQ02, m es la masa asociada al modo vibracional descrito por la coordenada nuclear Q y donde Q0 representa la separación de coordenadas de los dos mínimos de potenciales electrónicos La frecuencia de Bohr ω0 viene dada por ω0=E2k−E1j/ℏ. Ahora es necesario hacer una descripción de los momentos dipolares permanentes y de transición en los estados adiabáticos para la extensión de las ecuaciones ópticas convencionales de Bloch.

4. MOMENTOS DIPOLARES PERMANENTES Y DE TRANSICIÓN EN LOS ESTADOS ADIABÁTICOS

En nuestro modelo, los momentos dipolares permanentes y de transición entre los estados ψA y ψBse pueden escribir como:   

Con r=A,B, y donde m11 y m22 representan los momentos dipolares permanentes asociados a los estados desacoplados ψ1 y ψ2. En este caso:

Donde m es el operador de momento dipolar electrónico, para valores i,j=1,2. El factor de solapamiento vibracional χ1j|χ2k puede ser evaluado de acuerdo con la fórmula de Pekarian (^{Di Bartolo y Goldberg, 1980}):

Tenemos m11 y m22 evaluado en −Q0 y 0, respectivamente, mientras que las Ecs. (6) y (7), y dado el principio de Franck-Condon m12 se evalúa en −Q0. Esto equivale a evaluar los momentos permanentes y de transición en los estados desacoplados en la geometría de equilibrio. Sin embargo, estas geometrías se mezclan en la evaluación de los momentos en los estados acoplados. En las ecuaciones (6-8), primero observamos que, aun cuando los estados desacoplados tienen un momento dipolar permanente nulo m11=m22=0, el acoplamiento induce un momento no nulo en los estados acoplados proporcionados m12≠0. En segundo lugar, cuando m11, m22 son diferentes de cero, un caso importante en este trabajo, las contribuciones de m11 y m22 a μaaa=A, B pueden diferir sustancialmente debido tanto al factor de acoplamiento como al de Franck-Condon, mientras que la única manera en que los momentos del dipolo permanente m11 y m22 y contribuyen a μAB es a través de la diferencia m11−m22. En particular, cuando m11=m22≠0, estos momentos del dipolo permanente contribuyen a μaaa=A, B haciendo μbb diferente de μAA lo cual tiene consecuencias importantes para las respuestas no lineales. En tercer lugar, el interesante efecto del momento de transición μAB que va en sentido inverso al de los momentos del dipolo permanente mencionados anteriormente, según el cual μAB puede desaparecer como efecto del acoplamiento intramolecular a pesar de que el momento del dipolo de transición en el estado desacoplado m12≠0. Esto es, v=−m12E1j−E2k/m22−m11 y considerando esta expresión para el degenerado, las condiciones para el efecto mencionado son: i) los dos estados mezclados por el acoplamiento intramolecular deben ser no degenerados; y ii) los signos de m12E1j−E2k y m22−m11 deben ser opuestos. En cuarto lugar, el caso degenerado, E1j=E2k merece una atención especial. En este caso μAB y μaaa=A, B se convierten   

empleando el signo negativo en el estado A y el signo positivo para el estado B.

Los momentos de transición y de dipolo permanente son ahora independientes del acoplamiento v, además μAB, no contiene ninguna contribución de m12.

Estos resultados no se mantendrán exactamente para una función de onda más general:

Ψr,Q=Cij ψ1r;Qχ1jQ+C2k ψ2r;Qχ2kQpero un argumento perturbativo indica que incluso para una mezcla más general, las ecuaciones. (10) y (11) se mantendrán aproximadamente si hay una contribución dominante de cualquiera de los dos estados degenerados.

5. ECUACIONES ÓPTICAS DE BLOCH EN ESTADOS ADIABÁTICOS

Es importante destacar que nuestro sistema molecular aislado es representado en la base adiabática correspondiente a los estados A y B. Para estudiar la extensión de las ecuaciones de Bloch ópticas convencionales, ahora en la base adiabática, este sistema que hemos descrito estará sujeto a la interacción por la presencia del solvente, y a una interacción radiativa por efecto de los campos electromagnéticos. En orden de describir la evolución temporal del sistema, hacemos uso de la ecuación de Liouville dada por iℏ∂tρ=H,ρ, donde ρt es la matriz densidad reducida, mientras H es el Hamiltoniano total, el cual describe al soluto, solvente, capos electromagnéticos y todas las interacciones entre ellos, dado por H=HS+ HF+HR+HSF+HSR+HFR. Ahora HS corresponderá al Hamiltoniano del sistema aislado sujeto al efecto intramolecular y descrito por HS=H0+H˜r, donde H0 corresponderá al Hamiltoniano en la base diabática, mientras que H˜r representará la perturbación relativa al acoplamiento intramolecular; HR representa el Hamiltoniano del reservorio térmico, el cual es despreciado en el presente estudio; HF corresponde al Hamiltoniano del campo electromagnético, el cual no tomamos en cuenta por la consideración de la aproximación semiclásica. Para completar la descripción espectroscópica de interacción radiación-materia, consideraremos HSF para representar la interacción entre el soluto (sistema activo con acoplamiento intramolecular) y el campo, el cual describimos de acuerdo con la aproximación de tipo dipolar; HSR representa la interacción soluto-solvente descrita en términos de los mecanismos de relajación, y finalmente HFR que representa la interacción entre el campo de radiación y el solvente. Esta última interacción no la tomamos en cuenta, al considerar que la frecuencia del campo perturbador no es sintonizable o resonante a la frecuencia de respuesta del reservorio térmico. Normalmente se dice en este último que el solvente es transparente a la radiación, dado que no hay absorción. En orden de obtener la evolución temporal del sistema global, debemos considerar previamente algunas aproximaciones, algo más fundamentales. Suponemos un reservorio térmico con muchísimos grados de libertad, de forma que la interacción con el soluto la energía sea disipada rápidamente, haciendo que el reservorio permanezca en el régimen de equilibrio térmico. Este hecho se traduce en que ρtS−R=ρtS⊗ρ0R, además de considerar que el sistema en su interacción con el campo electromagnético pierde su memoria y evoluciona a partir del momento que interacciona con el campo. Esto último corresponde a la aproximación Markoviana. Una revisión más detallada de las restantes aproximaciones fundamentales que tienen lugar en este conjunto de interacciones puede ser revisada en la referencia (^{Blum, 1981}). Considerando entonces las interacciones mencionadas, y haciendo uso de la teoría cuántica de relajación, la evolución temporal del elemento de matriz densidad reducida, sólo para el subsistema, queda expresada de la forma:

donde Rm'mn'n es la matriz de relajación, cuya forma exacta puede ser vista en la referencia indicada, pero su deducción completa no es colocada en el presente trabajo. Nótese que la expresión (12) obedece a la evolución temporal de una parte reducida del sistema, adjudicada al subsistema, distinto a lo que ocurre en la ecuación de Liouville, la cual permite la evolución sólo de sistemas completos. Las ecs. (6) y (7) constituyen el punto central de este trabajo. En ellas se incluyen los efectos de la base acoplada (acoplamiento intramolecular) sobre el sistema de dos niveles, el ensanchamiento homogéneo de la línea espectral y la interacción del sistema con el reservorio. En este trabajo, hemos considerado que la presencia del reservorio térmico no modifica parámetros fundamentales en la respuesta del soluto. El primer término de la ec.(12) describe el sistema molecular acoplado con su frecuencia de resonancia ωm'm=ω˜0 (frecuencia de Bohr en la base adiabática); el segundo término es relativo a la interacción de carácter dipolar eléctrico entre el sistema y el campo de radiación, mientras que el último término, corresponde al mecanismo de relajación del sistema introducido en forma fenomenológico y representado por la matriz de Bloembergen del tipo Rm'mn'n (^{Blum, 1981}). Con todas estas consideraciones en mente, la dinámica del sistema es obtenida resolviendo las siguientes ecuaciones de Bloch ópticas para los estados adiabáticos: 

donde

ρ=ρABρBAρD;Mt=0fviℏμABEf∗v0−iℏμBAE−2iℏμABE2iℏμBAE−1T1 con fv=iω˜0−1T2−iℏdE R=001T1ρD0;d=μBB−μAAdonde fv es definida como la función de acoplamiento; ω˜0=EB−EAℏ ; donde E es la amplitud del campo electromagnético; T1 y T2 representan los tiempos de relajación longitudinal y transversal, respectivamente; ρD≡ρAA−ρBB representan la diferencia de población entre los estados electrónicos adiabáticos; el superíndice (0) denota el valor de equilibrio en la diferencia poblacional en la ausencia de radiación. En términos del acoplamiento vibrónico, las cantidades de importancia que definen el Hamiltoniano de interacción radiación-materia, se definen de la forma:     

Es posible recuperar la dinámica del sistema (en su conjunto con la presencia del reservorio térmico e interactuando con la perturbación radiativa) en la representación diabática, haciendo la perturbación H˜ pequeña, por lo que v→0. Finalmente, las ecuaciones de Bloch ópticas convencionales en presencia del acoplamiento vibrónico, quedan definidas de la forma:     

Como puede observarse tanto en las coherencias como en las poblaciones, la dinámica queda definida en términos de los parámetros del acoplamiento, pero tiene información de las bases diabáticas como función de sus momentos dipolares. Tal como lo señalamos anteriormente, en la base diabática el sistema puede tener momentos dipolares permanentes nulos, y sin embargo el correspondiente momento dipolar en los estados adiabáticos no necesariamente son ceros. Esto obliga a que en el cálculo no se considere la aproximación de onda rotante y haya que incorporar en el cálculo todos aquellos términos de anti-resonancia. Sin embargo, en la representación adiabática esta consideración ya no es determinante y por ende los resultados pueden concebirse sin la consideración de inclusión de términos que están fuera de resonancia.

6. COMENTARIOS FINALES

El modelo presentado en esta contribución representa una generalización o extensión de las ecuaciones ópticas de Bloch convencional en el régimen local de propagación. Normalmente en este tipo de ecuaciones locales no se consideran de forma explícita los momentos dipolares permanentes, ya que considerarlos hace que el tratamiento sea muy complejo y extenso por no poder hacer uso de la aproximación de la onda rotante. En un esquema perturbativo, incluir términos de anti-resonancia y estar fuera de la aproximación mencionada, requiere consideraciones muy particulares para evaluar las convergencias de los términos que escalan muy rápidamente, por ejemplo, cuando se trata interacción radiación-materia en el caso de mezcla de ondas tipo Rayleigh. Sin embargo, nuestra propuesta al convertir a la nueva base de estados adiabáticos, permite incorporar de forma natural los dipolos permanentes, los cuales son funciones de los dipolos en la base diabática, y estos últimos, pueden o no ser iguales a cero, pero el tratamiento no requiere condiciones de estar fuera de la aproximación de onda rotante. Esto hace, que nuestra propuesta, sea de utilidad para el estudio de los procesos de absorción de dos fotones, que normalmente se le estudia bajo consideraciones explicitas de momentos dipolares permanentes distintos de cero y tomando en cuenta los términos de anti-resonancia. Nuestro modelo puede ser aplicado a moléculas que presentan efectos del tipo Jahn-Teller o en los casos de estados excitados de dímeros. La restricción se cumplirá para los estados vibratorios casi degenerados en el llamado caso de acoplamiento débil.