INTRODUCCIÓN
El hormigón armado es el material más usado en la industria de la construcción en el Ecuador. Las propiedades mecánicas que adquiere el hormigón dependen en gran medida de la calidad de cada uno de sus componentes, así como del volumen que ocupan dentro de la mezcla. El módulo estático de elasticidad del concreto es una propiedad mecánica que permite caracterizar el comportamiento elástico del concreto, el cual puede ser obtenido aplicando cargas conocidas sobre un espécimen para evaluar la deformación del material ( Serrano & Pérez, 2010 ). La relación agua-cemento es otro factor importante, ya que a menor relación agua-cemento, mayor es la resistencia a la compresión. Según el ( American Concrete Institute, 2015 ) el Módulo estático de elasticidad se puede calcular usando la resistencia a la compresión del hormigón, y su valor se ve incrementado cuando la resistencia del hormigón es mayor. La ecuación que establece el ( American Concrete Institute, 2015 ) para el cálculo del módulo estático de elasticidad del hormigón es la siguiente:
Donde Ec es el módulo estático de elasticidad del hormigón en MPa y f’c es la resistencia a la compresión del hormigón en MPa. Esta recomendación del ( American Concrete Institute, 2015 ) ha sido replicada en la ( Norma Ecuatoriana de la Construcción, 2015 ). En su capítulo NEC_SE_HM se establece que el módulo estático de elasticidad del hormigón se puede calcular mediante la siguiente expresión:
Donde Ec es el módulo estático de elasticidad del hormigón en GPa y f’c es la resistencia a la compresión del hormigón en MPa.( )
En el Ecuador, se han realizado varios estudios para comprobar que esta ecuación es válida para el cálculo del módulo estático de elasticidad utilizando agregados locales. A continuación, se presenta un cuadro con los resultados obtenidos.
Tabla 1 Resultados de estudios realizados para determinar el módulo estático de elasticidad del hormigón con materiales de distintas minas en el Ecuador.
| Procedencia del Material | f 'c obtenido | Módulo de elasticidad (MPa) | Relación | |
|---|---|---|---|---|
| Teórico | Experimental | Experimental / teórico | ||
| (MPa) | ACI318-14 | ASTM-C469 | ||
| Mitad del Mundo (Pichincha) ( Espinoza & Martínez, 2010) | 20,40 | 21 341,90 | 11 505,89 | 53,91% |
| Mitad del Mundo (Pichincha) ( Espinoza & Martínez, 2010) | 23,30 | 22 815,97 | 13 447,32 | 58,94% |
| Mitad del Mundo (Pichincha) ( Espinoza & Martínez, 2010) | 26,70 | 24 418,20 | 13 842,30 | 56,69% |
| Pifo (Pichincha) ( Herrería & Villegas, 2008) | 35,00 | 27 805,57 | 20 483,60 | 73,67% |
| Pifo (Pichincha) ( Herrería & Villegas, 2008) | 35,70 | 28 082,25 | 20 647,90 | 73,53% |
| Pifo (Pichincha) ( Herrería & Villegas, 2008) | 35,70 | 28 082,25 | 20 309,30 | 72,32% |
| Pifo (Pichincha) ( Herrería & Villegas, 2008) | 35,00 | 27 805,57 | 20 700,00 | 74,45% |
| Mina de Guayllabamba (Pichincha) ( Morales, Ojeda, Rodríguez, & Rosero, 2012 ) | 30,97 | 26 155,83 | 24 370,26 | 93,17% |
| Mina de Guayllabamba (Pichincha) ) ( Morales, Ojeda, Rodríguez, & Rosero, 2012 ) | 35,19 | 27 880,95 | 24 574,11 | 88,14% |
| Mina San Ramón (Cotopaxi) ) ( Carvajal, 2013 ) | 28,74 | 25 196,56 | 18 587,95 | 73,77% |
| Mina San Ramón (Cotopaxi) ( Rivadeneira, 2013 ) | 30,14 | 25 802,96 | 19 018,93 | 73,71% |
| Mina San Ramón (Cotopaxi) ( Yanchal, 2013 ) | 31,49 | 26 374,50 | 19 232,96 | 72,92% |
| San Joaquín (Cotopaxi) ( Arequipa, Coba, Garzón, & Vargas, 2013 ) | 26,71 | 24 290,41 | 16 583,22 | 68,27% |
| San Joaquín (Cotopaxi) ( Arequipa, Coba, Garzón, & Vargas, 2013 ) | 30,18 | 25 820,07 | 18 323,13 | 70,96% |
| Mina Villacres (Tungurahua) ( Ulloa, 2013 ) | 30,50 | 25 956,60 | 19 212,73 | 74,02% |
| Mina Villacres (Tungurahua) ( García, 2013 ) | 33,03 | 27 011,71 | 20 087,08 | 74,36% |
| Mina Villacres (Tungurahua) ( Anasi, 2013 ) | 34,90 | 27 765,82 | 20 629,59 | 74,30% |
| Playa Llagchoa, Villacrés y de la Planta Industrial de Trituración de Áridos. (Tungurahua) ( Sánchez, 2013 ) | 21,00 | 21 538,11 | 19 073,56 | 88,56% |
| Playa Llagchoa, Villacrés y de la Planta Industrial de Trituración de Áridos. (Tungurahua) ( Sánchez, 2013 ) | 24,00 | 23 025,20 | 20 569,76 | 89,34% |
| Playa Llagchoa, Villacrés y de la Planta Industrial de Trituración de Áridos. (Tungurahua) ( Sánchez, 2013 ) | 28,00 | 24 870,06 | 22 465,80 | 90,33% |
Al observar los resultados obtenidos en investigaciones previas es evidente que el módulo estático de elasticidad obtenido de forma experimental es diferente al obtenido de forma teórica usando la ecuación planteada por el American Concrete Institute y la norma ecuatoriana de la construcción.
2. IMPORTANCIA DEL ESTUDIO
Para estimar deformaciones debidas a cargas de corta duración, donde se puede admitir un comportamiento elástico sin errores importantes, es necesario definir un valor del módulo estático de elasticidad ( Cuevas & Fernández, 2005 ). Todas las obras civiles para su cálculo y diseño dependen del Módulo estático de elasticidad. En el Ecuador, el material de mayor consumo dentro del campo de la construcción es el hormigón ( Diario El Universo, 2018), de aquí la importancia de contar con datos experimentales que comprueben que la forma de cálculo propuesta por el ( American Concrete Institute, 2015 ), que permite determinar el Módulo estático de elasticidad en función de la resistencia a la compresión, es aplicable a los hormigones fabricados con materiales que se encuentran en el Ecuador. En el control de calidad del hormigón en las obras civiles se da mayor importancia al valor de la resistencia a la compresión. Sin embargo, se debe considerar que el valor del módulo estático de elasticidad real del hormigón es igual de importante. El control de este parámetro tiene por objeto asegurar que la estructura se comporte de la forma en la fue diseñada ( Guaño, 2015 ). Como un aporte al desarrollo de la construcción en el Ecuador, se realizó este estudio utilizando materiales de la mina San Roque - Cantón Antonio Ante - Provincia de Imbabura.
3. DESCRIPCIÓN DEL ENSAYO
3.1 Propiedades de los materiales y diseño de mezclas.
Previo a realizar el diseño de mezclas, es necesario determinar las propiedades mecánicas de los agregados ( American Society for Testing and Materials, 2014 ). Los agregados usados en la fabricación del hormigón fueron obtenidos de la mina de San Roque ubicada en la provincia de Imbabura, Ecuador. En los agregados se realizaron ensayos de abrasión, colorimetría, masa específica, capacidad de absorción, contenido de humedad, densidad aparente suelta y compactada, densidad óptima y granulometría. En el cemento se realizó ensayos de densidad absoluta y consistencia normal. Los resultados obtenidos se muestran a continuación.
Tabla 2 Propiedades mecánicas del agregado grueso obtenido de la mina se San Roque, Imbabura, Ecuador
| Propiedades mecánicas de los materiales | Valor |
|---|---|
| Tamaño nominal máximo (Pulgadas) | 1,50 |
| Densidad suelta (g/cm3) | 1,31 |
| Densidad compactada (g/cm3) | 1,47 |
| Densidad saturado superficie seca (g/cm3) | 2,54 |
| Porcentaje de absorción (%) | 2,64 |
| Abrasión (%) | 47,54 |
Tabla 3 Propiedades mecánicas del agregado fino obtenido de la mina se San Roque, Imbabura, Ecuador
| Propiedades mecánicas de los materiales | Valor |
|---|---|
| Módulo de finura | 3,26 |
| Densidad suelta (g/cm3) | 1,63 |
| Densidad compactada (g/cm3) | 1,82 |
| Densidad saturado superficie seca (g/cm3) | 2,61 |
| Porcentaje de absorción | 2,22 |
Una vez obtenidas las propiedades mecánicas de los agregados, se realizó el diseño de mezclas usando el método ( American Concrete Institute, 2002 ) cuyo procedimiento se estableció por el comité 211. El diseño se lo realizó para obtener resistencias de 26MPa y 30MPa.
3.2 Descripción de las probetas
Usando el diseño de mezclas obtenido mediante el método del ACI, se construyeron 18 cilindros de hormigón cuya resistencia esperada fue de 26MPa y 18 cilindros de hormigón cuya resistencia esperada fue de 30MPa. Las dimensiones de los cilindros fueron de 150mm de diámetro y 300mm de altura. Estas dimensiones son estándar para la norma ACI y también para el Ecuador (Instituto Ecuatoriano de Normalización, 2011). Los 18 cilindros fueron ensayados para obtener la resistencia a la compresión del hormigón. Las resistencias obtenidas fueron las mismas para las cuales se diseñó la mezcla, por lo tanto, se usó este diseño de mezclas para elaborar las probetas con las cuales se obtuvo el módulo estático de elasticidad.
3.3 Módulo estático de elasticidad experimental
Para obtener el módulo estático de elasticidad experimental se utilizó el procedimiento establecido en la norma ASTM C 469 ( American Society for Testing and Materials, 2014) que establece que el módulo de rigidez experimental se puede determinar mediante la siguiente ( American Society for Testing and Materials, 2014):
En donde E es el módulo estático de elasticidad del hormigón en MPa, σr es el esfuerzo máximo en MPa que soporta la probeta, 𝜎1 es el esfuerzo en MPa correspondiente a una deformación unitaria de 0,00005 y 𝜀𝑥 es la deformación unitaria que ocurre para el esfuerzo de 0,40𝜎𝑟.
Una vez obtenidas las resistencias de diseño requeridas, se construyeron 30 cilindros de 150mm de diámetro y 300mm de altura de resistencias de 26MPa y 30MPa. 20 de estos cilindros fueron utilizados para realizar ensayos de compresión. Se ensayaron 5 cilindros a los 7 días, 5 cilindros a los 14 días, 5 cilindros a los 21 días y 5 cilindros a los 28 días. Los 10 cilindros restantes se utilizaron para obtener el módulo estático de elasticidad. Para la resistencia de 26MPa se consideraron 9 cilindros para el cálculo del módulo estático de elasticidad. Para la resistencia de 30MPa se consideraron 8 cilindros para el cálculo del módulo estático de elasticidad. Esto debido a que tres cilindros en total se descartaron debido a que presentaban errores en su fabricación.
3.4 Ensayo
El procedimiento para obtener el módulo estático de elasticidad es el que se indica en la norma ASTM C469. Los pasos son los siguientes: En la probeta, se colocan abrazaderas unidas mediante pivotes. Las abrazaderas se unen a la probeta usando puntos de sujeción al eje de la misma. Finalmente se coloca un deformímetro para medir la deformación que se presenta en la probeta debido a la carga de compresión. Un esquema de los componentes colocado en la probeta se muestra a continuación.
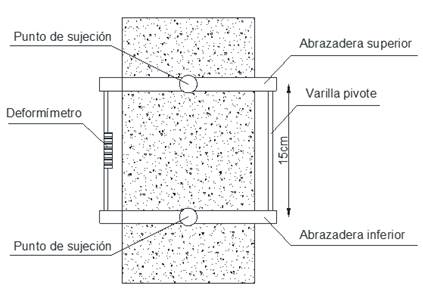
Figura 1 Esquema de colocación de equipos en la probeta para determinar el módulo estático de elasticidad del hormigón.
Los datos del ensayo fueron recopilados por dos observadores. El primero reportó la carga aplicada a la probeta, el otro observador reportó la deformación que se presentó en la probeta. El valor que se lee en el deformímetro se divide entre 2 debido al esquema con el cual se miden las deformaciones. Figura 1
Se utilizaron dos ciclos de carga. El límite para el primer ciclo de carga fue de 400kN. Esto debido a que el esfuerzo correspondiente a esta carga es aproximadamente 22,60MPa. Este valor supera el 40% de esfuerzo máximo para el cual las probetas fueron diseñadas. Estos datos son suficientes para determinar el módulo estático de elasticidad del hormigón ya que el mismo se calcula usando una deformación unitaria correspondiente al 40% del esfuerzo máximo que soporta la probeta ( American Society for Testing and Materials, 2014). Para el segundo ciclo de carga no existió límite, se aplicó carga a la probeta hasta que se produjo la falla a compresión.
4. RESULTADOS ESPERADOS
4.1 Resistencia a la compresión
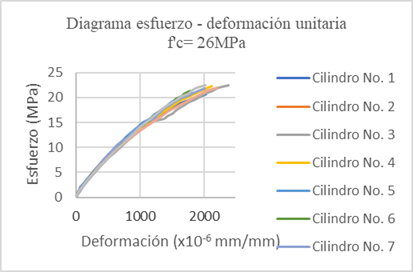
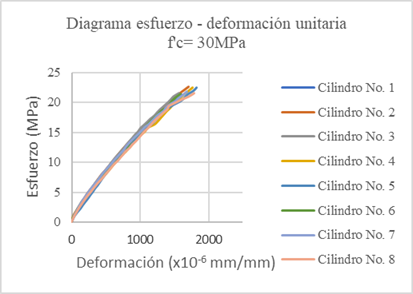
De acuerdo con el diseño de mezclas utilizado para elaborar el primer grupo de especímenes de hormigón, la resistencia esperada es de 26MPa. Para el segundo grupo de especímenes, se utilizó un diseño de mezclas cuya Resistencia esperada es de 30MPa.
4.2 Módulo estático de elasticidad
El módulo estático de elasticidad esperado se calcula considerando la resistencia a la compresión esperada ( American Concrete Institute, 2015 ), para ello se utiliza la ecuación (1). El valor esperado para el módulo estático de elasticidad del hormigón de 26MPa es 23965,39MPa. El valor esperado para el módulo estático de elasticidad del hormigón de 30MPa es de 25742,96MPa.
5. RESULTADOS OBTENIDOS
5.1 Resistencia a la compresión
La resistencia a la compresión promedio obtenida para el primer diseño de mezclas fue de 26,71MPa. Para el segundo diseño de mezclas, la resistencia a la compresión obtenida fue de 30,86MPa. Estos valores son muy cercanos a los cuales se esperaba obtener. Figura 3
5.2 Diagrama esfuerzo - deformación unitaria de las probetas.
Con los datos recopilados por los observadores se obtuvieron los diagramas esfuerzo deformación para cada cilindro. Estos diagramas fueron usados para determinar el módulo estático de elasticidad del hormigón. Figura 2
5.3 Módulo estático de elasticidad del hormigón
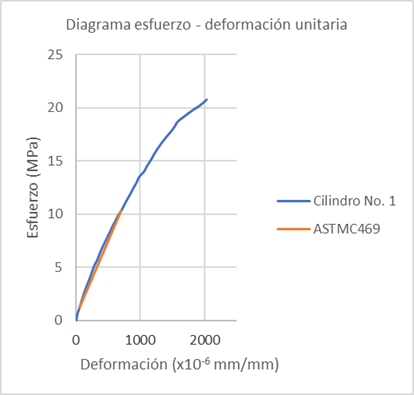
El módulo estático de elasticidad se obtuvo utilizando la ecuación (3). A continuación, se muestra un diagrama de esfuerzo deformación en el cual se ha colocado la recta cuya pendiente se define como el módulo estático de elasticidad del hormigón. Figura 4
El módulo estático de elasticidad obtenido experimentalmente, para una resistencia a la compresión de 26,71MPa fue de 14368,07MPa. El módulo estático de elasticidad obtenido experimentalmente para una resistencia a la compresión de 30,86 MPa fue de 14818,07MPa. Figura 5
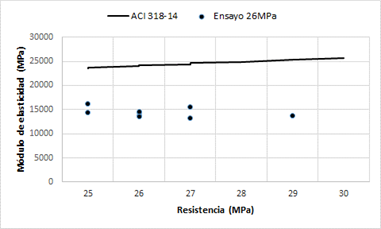
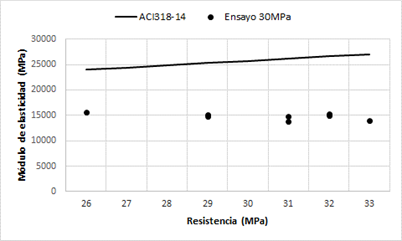
Figura 5 Comparación módulo estático de elasticidad teórico y experimental para una resistencia a la compresión de 26MPa.
6. ANÁLISIS DE RESULTADOS
En cuanto a la resistencia a la compresión, los resultados esperados y los resultados experimentales tiene valores muy similares. En cuanto al módulo estático de elasticidad, los resultados teóricos y experimentales presentan valores muy diferentes. A continuación, se presenta un cuadro comparativo de los resultados obtenidos para el módulo estático de elasticidad. Figura 6
Tabla 4 Resultados de resistencia a la compresión y módulo estático de elasticidad.
| Resistencia a la compresión (MPa) | Módulo de elasticidad (MPa) | Módulo de elasticidad (MPa) |
| ACI318-14 | ASTM C469-64 | |
| Teórico | Experimental | |
| 26,71 | 24290,41 | 14368,07 |
| 30,86 | 26109,34 | 14818,07 |
El módulo estático de elasticidad teórico fue calculado usando la ecuación (1). El módulo estático de elasticidad experimental se calculó usando lo establecido en la norma ASTM C469 ( American Society for Testing and Materials, 2014).
Claramente se observa que los resultados teóricos y experimentales del módulo estático de elasticidad son muy diferentes.
Si estos valores se expresan en porcentaje, para el primer diseño de mezclas, el módulo estático de elasticidad obtenido experimentalmente es el 59,15% respecto al valor teórico. En el segundo diseño de mezclas, el módulo estático de elasticidad obtenido experimentalmente es del 56,75% respecto al valor teórico.
Usando estos resultados, se obtuvieron coeficientes que relacionen la resistencia del hormigón con el módulo estático de elasticidad. El coeficiente obtenido en esta investigación es de 2 780,11 para una resistencia a la compresión de 26,71MPa. Es decir, adoptando el formato de la ecuación (1), el módulo estático de elasticidad se podría calcular con la siguiente expresión:
Para la resistencia a la compresión de 30.86MPa, el coeficiente obtenido es de 2667.43. Adoptando nuevamente el formato de la ecuación (1) el módulo estático de elasticidad se podría calcular con la siguiente expresión:
En esta investigación, se propone usar la ecuación (5) en lugar de la ecuación (1) para obtener el módulo estático de elasticidad del hormigón si se fabrica utilizando como agregados los materiales obtenidos de la mina de San Roque ubicada en Imbabura, Ecuador.
Se propone la ecuación (5) y no la (4) debido a que la ecuación (5) es más conservadora.
En resumen:
En la presente investigación se realizaron dos diseños de mezclas de hormigón, se elaboraron probetas y se ensayaron a compresión. Adicionalmente, se obtuvo de forma experimental el módulo estático de elasticidad del hormigón para compararlo con el módulo estático de elasticidad teórico.
El primer diseño de mezclas dio como resultado una resistencia a la compresión de 26,71MPa.
Para este diseño de mezclas se obtuvo el módulo estático de elasticidad experimental del hormigón usando el método establecido por la ASTM C469 ( American Society for Testing and Materials, 2014), el resultado obtenido fue de 14368,07MPa.
El resultado teórico del módulo estático de elasticidad para el primer diseño de mezclas, considerando que su resistencia a la compresión fue de 26,71MPa, es de 24290,4MPa.
Para este diseño, el módulo estático de elasticidad obtenido experimentalmente es el 59,15% respecto al valor teórico.
El segundo diseño de mezclas dio como resultado una resistencia a la compresión de 30,86MPa.
Para este diseño de mezclas se obtuvo el módulo estático de elasticidad experimental del hormigón usando el método establecido por la ASTM C469 ( American Society for Testing and Materials, 2014) el resultado obtenido fue de 14818,07MPa.
El resultado teórico del módulo estático de elasticidad para este diseño de mezclas, considerando que su resistencia a la compresión fue de 30,86MPa, es de 26109,30MPa.
Para este diseño, el módulo estático de elasticidad obtenido experimentalmente es el 56,75% respecto al valor teórico.
7. CONCLUSIONES
Se evidencia que, en ninguno de los dos ensayos de laboratorio, los resultados del módulo estático de elasticidad del hormigón obtenidos experimentalmente son iguales a los obtenidos de forma teórica con la ecuación (1), la cual es establecida por el ( American Concrete Institute, 2015 ).
Esta diferencia en los resultados se presenta debido a que el módulo de elasticidad del hormigón puede variar dependiendo de las propiedades de los agregados. Esto implica la necesidad de obtener datos experimentales de los agregados utilizados en cada región del país.
El ( American Concrete Institute, 2015 ), de acuerdo con la ecuación (1) establece que el módulo estático de elasticidad se puede calcular utilizando la resistencia a la compresión del hormigón; sin embargo, en los ensayos realizados se observa que, aunque se incrementa la resistencia a la compresión, no se incrementa significativamente el módulo estático de elasticidad del hormigón.
( American Concrete Institute, 2015 ) establece que el módulo estático de elasticidad del hormigón es sensible al módulo estático de elasticidad del agregado y a la dosificación de la mezcla de concreto y que los valores medidos del módulo estático de elasticidad pueden varían entre el 80 y el 120 por ciento de los valores calculados. Sin embargo, en este estudio, la variación fue de hasta el 56 por ciento.
De acuerdo con los resultados obtenidos, no es conveniente utilizar la ecuación (1), que establece el ( American Concrete Institute, 2015 ) para calcular el módulo estático de elasticidad del hormigón en todas las regiones. Esto debido a que las características de los agregados varían en cada región.
En el código NEC-15 ( Norma Ecuatoriana de la Construcción, 2015 ) en la sección 3.3.3 se establece la forma de cálculo del módulo estático de elasticidad para el hormigón. Esta ecuación es la misma que se utiliza en el ( American Concrete Institute, 2015 ). Por lo tanto, la forma de cálculo del módulo estático de elasticidad en la ( Norma Ecuatoriana de la Construcción, 2015 ) tampoco se puede aplicar para el agregado obtenido de la mina San Roque, Imbabura.
Es necesario establecer una forma de cálculo del módulo estático de elasticidad del hormigón para cada país o región debido a la diferencia en las características de los agregados que se utilizan en la fabricación del hormigón.
En esta investigación se sugiere la siguiente expresión para el cálculo del módulo estático de elasticidad del hormigón cuando se fabrique usando agregados de la mina de San Roque, Imbabura.
Es necesario realizar investigaciones del mismo tipo para las minas principales de la cuales se extraen los agregados para elaborar hormigón en el Ecuador, esto con el fin de lograr una mejor estimación en el cálculo del módulo estático de elasticidad del hormigón.( )
El cálculo adecuado en el módulo estático de elasticidad del hormigón permitirá que no se subestimen las deformaciones en las estructuras de hormigón armado.
La ( Norma Ecuatoriana de la Construcción, 2015 ) establece que la deriva máxima de piso en estructuras de hormigón armado debe ser de 0.02. La deriva de piso depende entre otros factores del módulo estático de elasticidad del hormigón. Sobreestimar el módulo estático de elasticidad del hormigón provocará que la deriva provocada en un movimiento sísmica sea mayor a la obtenida en el análisis estructural.