1. INTRODUCCIÓN
El crecimiento de zonas urbanas y rurales, así como el desarrollo industrial e infraestructura pública y privada en el sector del valle de Latacunga, provincia de Cotopaxi, presenta relación directa frente a la vulnerabilidad asociada a los flujos de lahar generados durante una posible erupción del volcán Cotopaxi. Luego de un período relativamente largo de inactividad, más de 140 años desde la última erupción representativa (Sodiro, 1877; Wolf, 1878), durante el último trimestre del año 2015 e inicios de 2016 se registró un nuevo periodo de reactivación de la actividad volcánica (IG-EPN, 2015). Ante este proceso natural que podría afectar negativamente extensas zonas ubicadas en sectores próximos a los cauces naturales de drenaje del flujo de lahar, se requiere información técnica actualizada relacionada con la ocurrencia de este fenómeno para contribuir al estudio y problemática particular que representa el flujo de lahares primarios producto de erupciones volcánicas en volcanes nevados.5 6 7 11 12 15 18 19 20 22 24 25 32 33 35 36 37 38 39 42 44 46 47 48 49 51 52 53 54 56 57 62 69
Para alcanzar este objetivo, se hace evidente la necesidad de llevar a cabo actividades concernientes a la recopilación y levantamiento de información de campo correspondiente principalmente a vestigios o evidencias físicas asociadas al evento eruptivo ocurrido en junio de 1877. Las actividades técnicas desarrolladas en las últimas décadas por el Instituto Geofísico de la Escuela Politécnica Nacional (IG-EPN), en varias campañas han permitido disponer de registros de campo sobre la caracterización geológica de los vestigios del evento eruptivo del año 1877 en varias secciones transversales representativas de la zona de estudio. Además, con base en el análisis de las muestras recuperadas, se ha caracterizado el tipo de lahar y su composición (Mothes et al., 2004; Mothes, 2006; Hall et al., 2008).
El avance tecnológico en relación a la generación de modelos digitales de terreno (MDT), que en el caso de esta investigación alcanza una resolución espacial de 3.0 metros por pixel, permite la representación adecuada de la topografía en el área de estudio. Esta información es utilizada para la modelación numérica del flujo de lahar empleando un paquete computacional de código libre para el análisis de flujo permanente y no permanente (no estacionario) que resuelve las ecuaciones de Saint Venant presentadas en forma de derivadas parciales en una dimensión, en la dirección del flujo de un volumen de control considerando los principios de conservación de masa y cantidad de movimiento (Vera, 2017).
El análisis numérico del flujo de lahares del volcán Cotopaxi ha sido ampliamente estudiado desde hace varias décadas tomando como referencia al evento eruptivo histórico del año 1877, considerando en ciertos casos, modelos numéricos sencillos asumiendo flujos homogéneos con volumen constante (Barberi et al., 1992). En lo reportado por Castro et al., 1992; Espín, 1993 y Sánchez, 1993, la modelación numérica de lahares del Cotopaxi se realizó con programas computacionales como el HEC-1, LAHAR-1 y DAMBRK (Costa, 1977) respectivamente. Se ha investigado los lahares y su impacto sobre ciudades como Latacunga con el programa TITAN2D (Williams, 2006). Según lo reportado por Lima, 2007, se realiza la simulación del flujo lahárico no permanente utilizando programas como el FLDWAV y HEC-RAS. En los estudios desarrollados por Samaniego, 2004; Pistolesi, 2014, se estudia los flujos de lahar mediante el uso del software LAHARZ (Iverson et al., 1998).
En varios casos, las condiciones iniciales de las simulaciones consideran la evidencia histórica geológica encontrada en los trabajos de campo como base de la modelación numérica e información topográfica correspondiente a modelos digitales de terreno para la representación del área de estudio.
2. EL VOLCÁN COTOPAXI
Es un estratovolcán ubicado en la cordillera Oriental o Real de los Andes Ecuatorianos, a 60 km al Sureste de Quito, su cráter se eleva hasta los 5 897 m.s.n.m. El cono del volcán se encuentra cubierto por un casquete glaciar que desciende desde la cima por todos los flancos del mismo.
La aparente uniformidad de su topografía se interrumpe ante la presencia de varias quebradas profundas, que constituyen el inicio o nacimiento de los cauces principales y ríos, los mismos que fluyen aguas abajo atravesando el valle de Latacunga en el drenaje Sur-Occidental, el valle de los Chillos hacia el Norte y además hacia el drenaje Oriental.
Desde mediados del mes de abril del año 2015, el IG-EPN reportó un incremento en la actividad eruptiva del volcán, alcanzándose un total de 300 sismos volcánicos y varias emisiones de dióxido de azufre (SO2) que precedieron a explosiones hidromagmáticas (Gaunt et al., 2016). La actividad superficial caracterizada por emisión de gas y ceniza continuó durante meses, registrándose un volumen de 860 mil metros cúbicos de ceniza (Bernard et al., 2016). Las características de este periodo eruptivo han permitido identificar a este evento con el Índice de Explosividad Volcánica VEI igual a 1 (VEI; Newhall & Self, 1982).
Según lo reportado por Jordan (1983), el área total del casquete glaciar cubría 21.3 km2 en el año 1976. Esta cobertura glaciar ha sufrido una reducción notable que continúa a través de los años, alcanzando valores totales de hasta 12.7 km2 en el año 2006 y aproximadamente 10.5 km2 para el año 2016 (Cáceres, 2016). Por analogía con la erupción del año 1995 del Nevado del Ruiz se estima una disminución en el espesor del glaciar de alrededor de 4 metros. Dado que el agua se libera de forma súbita el hidrograma tipo de estos flujos tendría una forma triangular, con un caudal dominante y una atenuación lenta con hidrogramas de iguales características a los utilizados para modelar los eventos laháricos de las erupciones del Mount. St. Helens y del Nevado del Ruiz (Pierson et al., 1990; Thouret, 1990) respectivamente.
Samaniego (2004) y Andrade et al. (2005) definieron escenarios eruptivos ante una posible erupción del volcán Cotopaxi en base a criterios como: Dinamismo eruptivo (tipos de erupciones que podrían ocurrir en el volcán), magnitud de las erupciones (establecida por trabajos de campo y distribución de los productos volcánicos), comportamiento de otros volcanes andesíticos (Tungurahua, Reventador y Sangay), grado de interacción entre los productos volcánicos y el glaciar (función de los dinamismos eruptivos), tamaño y porcentaje de fusión del glaciar.
En base a las características eruptivas de cada uno de los ciclos de actividad categorizados según el Índice de Explosividad Volcánica (VEI; Newhall & Self, 1982), se ha establecido, para el volcán Cotopaxi, cuatro escenarios que permiten determinar la probabilidad de ocurrencia de una erupción volcánica. Considerando aspectos como el índice de explosividad volcánica VEI, el tipo de actividad y los fenómenos eruptivos como la caída de ceniza, flujos piroclásticos, fragmentos balísticos y lavas, se determinan los siguientes escenarios eruptivos: Pequeño (Escenario 1: VEI 1-2), Moderado (Escenario 2: VEI 2-3), Grande (Escenario 3: VEI 3-4) y Muy grande (Escenario 4: VEI >4).
En los últimos 2000 años se han registrado al menos 19 eventos eruptivos importantes, el más reciente se ha catalogado con VEI igual a 1, se registra otros 6 eventos eruptivos con un VEI de 3 (se incluye un evento con un VEI de 2-3), adicionalmente se consideran 10 eventos con un VEI de 4 (se incluye un evento con un VEI de 3-4), y finalmente hay 2 eventos eruptivos con un VEI > 4 (Samaniego, 2004).
La secuencia cronológica presentada en la Tabla 1 permite plantear que el escenario con mayor probabilidad de ocurrencia es el Escenario No. 3, el cual está asociado a una erupción similar a la ocurrida en el año 1877 (VEI 3-4) asignándole un 58% de probabilidad. Según Samaniego (2004), luego de un ciclo de reposo relativamente extenso como el actual (más de 140 años), existe la posibilidad de que la actividad del volcán continúe y desencadene una erupción importante (VEI ≥3). Para los eventos mayores (Escenario 4: VEI >4) la probabilidad de ocurrencia alcanza el 10.5 %, mientras que los eventos menores (Escenario 2: VEI 2-3) presentan una probabilidad del 26.31%. La probabilidad de que un evento eruptivo produzca únicamente un flujo de lava es relativamente baja (2 erupciones en los últimos 2000 años, con probabilidad de 10.52%).
Tabla 1. Síntesis de la actividad volcánica del Cotopaxi en los últimos 2000 años. Samaniego (2004)
| Edad | Emisiones de ceniza | Flujopiroclástico | Lahares | Flujo de lava | VEI |
| 2015 DC | x | secundario | 1 | ||
| 1880 DC | x | 2-3 | |||
| 1877 DC | x | x | 2 | 4 | |
| 1854 DC | x | x | 1 | 1 | 3 |
| 1853 DC | x | 1 | 1 | 3 | |
| 1768 DC | x | x | 1 | 1 | 4 |
| 1766 DC | x | x | 1 | 3 | |
| 1744 DC | x | x | 2 | 4 | |
| 1742 DC | x | x | 3 | 4 | |
| 1532-34 DC | x | x | 2 | 1 | 4 |
| ~ 1150 DC | x | x | 2 | 4 | |
| ~1000 DC | x | x | 3 | ||
| 950 DC | x | x | 2 | >4 | |
| 850 DC | x | x | 1 | 3-4 | |
| 750 DC | x | x | 2 | 4 | |
| ~180 DC | x | x | 1 | varios | 4 |
| ~ 150 DC | x | x | 2 | 1 | >4 |
| ~ 100 DC | x | varios | 4 | ||
| 50 AC | x | x | 4 |
3. LA RED DE DRENAJE SUR
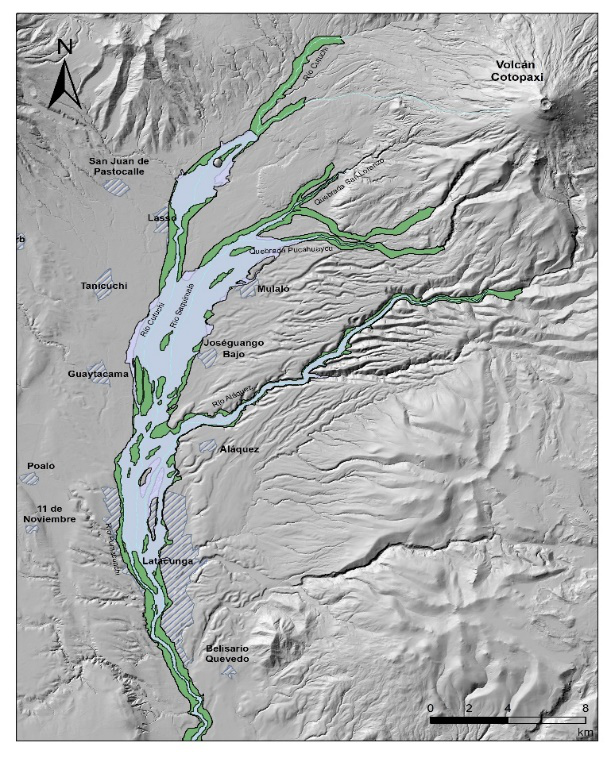
El entorno natural del área estudiada corresponde al drenaje Sur-Occidental que inicia en las faldas del volcán, donde el sistema de quebradas transporta, desde las once (11) lenguas de glaciar, los flujos de lahares hasta cauces más amplios y menos profundos (valle de Latacunga) con una longitud de 30 km que conforman el río Cutuchi, el cual atraviesa la ciudad y continua hacia el Sur donde presenta una morfología de cauce encañonado y profundo.
La red hidrográfica primaria del flanco Sur-Occidental está compuesta por los ríos Cutuchi, Saquimala y Aláquez. Estos cauces de drenaje natural fluyen desde la base del volcán y continúan por una llanura extensa de baja pendiente hacia el Sur y el Occidente. En el caso particular del río Pumacunchi, que pertenece a la cordillera Occidental, se observa que al desarrollarse en forma paralela y cercana al cauce del río Cutuchi puede ser afectado en el caso del desborde del lahar.
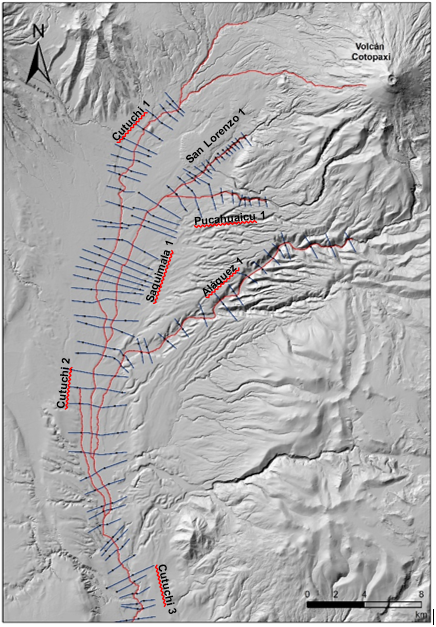
Se consideran cuatro tramos iniciales para representar la morfología alta o superior de la zona estudiada, cuyos nombres son: Cutuchi, San Lorenzo, Pucahuaicu y Aláquez. Conforme se desarrollan hacia el Sur-Occidente forman los tramos intermedios del río Cutuchi y Saquimala, que al unirse con el río Aláquez, conforman el tramo final del río Cutuchi. Las pendientes longitudinales representativas de los tramos considerados varían entre 1 y 10% y las longitudes de los cauces alcanzan valores desde 9 hasta 42 km.
La distribución radial del glaciar del Cotopaxi reportada por Cáceres (2016), referente a las áreas de aporte del drenaje Sur, permite identificar las lenguas glaciares, que se han denominado y numerado de acuerdo a lo siguiente: Tambo (9), Churrumihurco (10), Simarrones (11), El Picacho (12), Saquimala (13), San Lorenzo (14), Capuli-Huaicu (15), Pucahuaicu Oeste (16), Chanchunga Sur (17), Chanchunga Norte (18) y Yanasacha (19). Figura 1
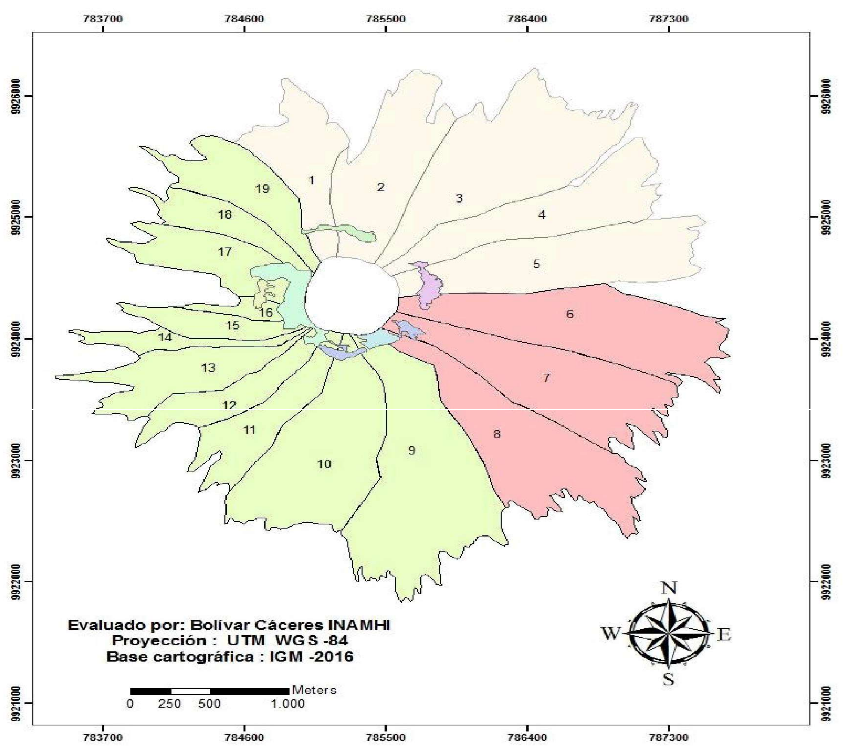
Figura 1. Distribución de glaciares del drenaje Sur-Occidental (áreas de color verde 9-19) del volcán Cotopaxi. Cáceres (2016)
En la Tabla 2 se presentan las áreas glaciares de drenaje entre los años 1977 y 2016 (Cáceres 2017), correspondientes a la zona Sur-Occidental. Los resultados obtenidos muestran la notable reducción de aproximadamente el 50% en la superficie glaciar, comparando las áreas totales de los años 1977 y 2016.
Tabla 2. Evolución de áreas glaciares del flanco Sur-Occidental entre los años 1977 y 2016. Cáceres (2017)
| # | Glaciar | Área 1977(m2) | Área 2016(m2) |
| 9 | Tambo | 893 101 | 1´183 565 |
| 10 | Churrumihurco | 1´348 900 | 894 343 |
| 11 | Simarrones | 1´585 600 | 362 736 |
| 12 | El Picacho | 1´403 500 | 275 678 |
| 13 | Saquimala | 1´177 174 | 402 897 |
| 14 | San Lorenzo | 1´192 300 | 137 166 |
| 15 | Capuli-Huaicu | 776 100 | 180 454 |
| 16 | Pucahuaicu Oeste | 426 872 | 62 377 |
| 17 | Chanchunga Sur | 382 600 | 325 413 |
| 18 | Chanchunga Norte | 712 300 | 239 722 |
| 19 | Yanasacha | 957 400 | 398 034 |
| Área Total | 10´855 847 | 4´462 385 |
Cabe señalar que en la etapa de calibración del modelo numérico se utiliza la información correspondiente al área del glaciar del año 1977, puesto que constituye la mejor aproximación al evento del año 1877 (VEI 3-4) debido a su elevada probabilidad de ocurrencia. Para la modelación numérica de los escenarios eruptivos actuales se emplea las áreas de glaciar en las condiciones actuales, las mismas que como se ha determinado, son relativamente menores a las del escenario de calibración (evento eruptivo histórico).
4. ANÁLISIS TEÓRICO / METODOLOGÍA
4.1 Breve caracterización reológica de lahares
Un lahar se define como una mezcla de sólidos y agua que fluye rápidamente por efecto de la gravedad. Está compuesto por bloques de roca, escombros, sedimentos y agua. Sus características pueden variar conforme transcurre el tiempo y la distancia que recorre hacia aguas abajo desde el inicio del evento en el pie del volcán. Entre los tipos de flujo que se presentan tenemos a los flujos de escombros, transicionales, hiperconcentrados y las inundaciones (Vera, 2017). Figura 2
Los factores que caracterizan un flujo lahárico son: ocurrencia repentina relacionada con el tipo de erupción, elevada tasa de avance que depende de las pendientes y la topografía, gran capacidad de transporte de sólidos que se van incorporando durante su recorrido, desarrollo en grandes distancias a lo largo de los cauces naturales y zonas inundables que generalmente albergan a poblaciones e infraestructura.
Los flujos de lahares alcanzan caudales máximos en tiempos relativamente cortos, erosionan cauces e incorporan material sedimentario que corresponde a depósitos de lahar existentes sobre el terreno originados por eventos anteriores. El volumen de agua presente en el lahar genera cantidades de material que pueden superar la capacidad hidráulica de los drenajes y provocan inundaciones y desbordamientos en zonas planas.
Según Coussot y Meunier (1995) los tipos de flujo se clasifican de manera conceptual y cualitativa en función del porcentaje de sólidos que componen la mezcla, la interacción de las partículas (cohesivas, no cohesivas, granulares, finos, etc.) y la fracción de sólidos (cuyo valor se incrementa desde agua a flujos con transporte de sólidos, flujos hiperconcentrados, flujos de escombros y avalanchas).
En la Figura 3 se presenta una clasificación en función de la fracción de sólidos y el tipo de material, de acuerdo a este esquema se puede clasificar a los lahares como una mezcla bifásica con movimiento rápido, que se encuentra entre los flujos de escombros (desperdicios) e hiperconcentrados.
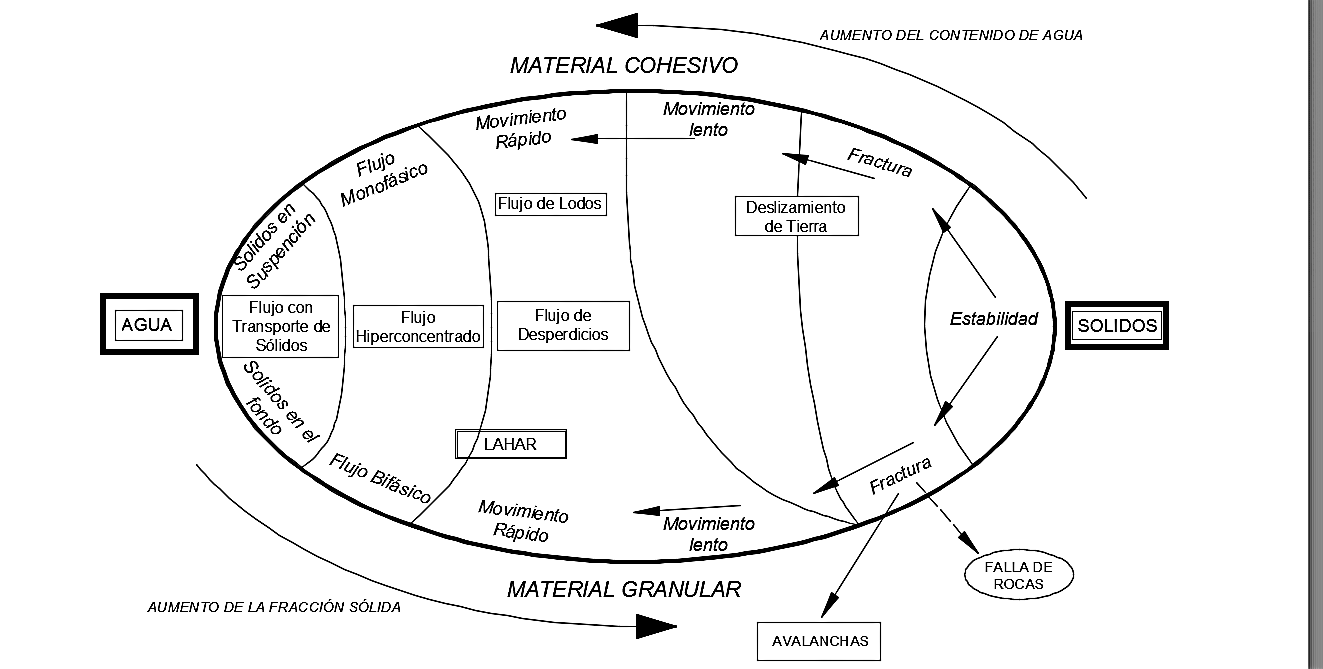
Figura 3. Clasificación de las mezclas de agua y sólido como función de la fracción de sólidos y el tipo de material. Coussot y Meunier (1995)
Estudios realizados en el drenaje Sur del volcán Cotopaxi permiten determinar las características físicas de los flujos de lahar de esta zona. Según Mothes et al. (2004), estos presentan características de flujos no cohesivos e hiperconcentrados con distribución casi uniforme de los granos que conforman la matriz del flujo. Esto se ratifica en estudios más recientes (CIERHI, 2017) que analizan la distribución del tamaño del grano en función del porcentaje acumulado de la muestra donde se observa un comportamiento como flujo granular y no cohesivo al clasificarlo en función del tamaño medio del grano y el sorteo representado como la variación de la muestra en relación a su valor promedio en cada sección. Figura 4
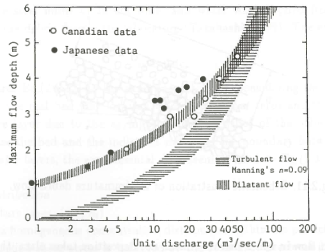
Figura 4. Comparación de caudales unitarios obtenidos para diferentes profundidades con flujos de escombros granulares. Takahashi (1991)
En la investigación experimental realizada por Takahashi (1991) se plantea que el comportamiento, tanto de un flujo dilatante (lahar) como de uno turbulento, tiende a ser similar conforme aumenta el valor de caudal unitario en relación al incremento de la profundidad de flujo. Esta observación permite plantear métodos de solución numérica de flujos laháricos como flujos Newtonianos, puesto que generalmente se consideran calados y caudales unitarios elevados.
4.2 Coeficientes de rugosidad (resistencia al movimiento)
Los coeficientes de rugosidad o “n” de Manning están relacionados con la resistencia al movimiento como características del cauce que generalmente están asociadas a la rugosidad superficial, presencia de vegetación, la forma y alineación del cauce.
La ecuación de Manning (Ganguillet y Kutter, 1889) involucra el término del coeficiente de rugosidad (n), el mismo que según lo reportado por Chow (1994) se expresa como:
Donde V es la velocidad media en (m/s), n el coeficiente de rugosidad o “n” de Manning, R es el radio hidráulico en (m) y S es la pendiente de la línea de energía (m/m).
Para Costa (1997), los flujos ricos en sedimentos o hiperconcentrados, pueden ser modelados utilizando coeficientes de resistencia al movimiento correspondientes a flujos dilatantes, sin embargo, requieren de una etapa de calibración que permita un análisis entre los resultados alcanzados y los datos de campo que generalmente están constituidos por vestigios de eventos pasados.
4.3 Modelación numérica unidimensional
La modelación numérica unidimensional se basa en la solución de las ecuaciones que describen el comportamiento de un flujo y cuyas características más relevantes son el caudal, velocidad, calado, resistencia al movimiento, entre otras. El modelo considerado para la simulación numérica se utiliza para las etapas de calibración y modelación unidimensional definitiva para flujos permanentes y no permanentes.
El modelo numérico unidimensional utilizado es HEC-RAS 5.0.3 de la U.S. Army Corps of Engineers, permite simular flujo uniforme gradualmente variado mediante la solución de la ecuación de la energía, donde las pérdidas se evalúan por fricción con la ecuación de Manning y tanto la expansión como la contracción en función de coeficientes multiplicados por las cargas de velocidad.
La ecuación de impulso o cantidad de movimiento es utilizada cuando el perfil de flujo es rápidamente variado. Las ecuaciones de continuidad y conservación de la cantidad de movimiento para flujos unidimensionales en canales abiertos se pueden expresar como se plantea a continuación (HEC-RAS, 2016):
Ecuación de Continuidad:
Ecuación de Cantidad de movimiento:
Donde es la sección transversal, es el tiempo, es el caudal, representa la distancia a lo largo del canal, es el caudal lateral por unidad de longitud, representa la velocidad, es la aceleración de la gravedad, representa el nivel de referencia del canal, es la pendiente de fricción.
La simulación numérica para flujo no permanente requiere la solución de las ecuaciones de Saint Venant. La necesidad de encontrar la solución a estas ecuaciones hizo que se desarrollen métodos simplificados que al despreciar algunas de las variables hidrodinámicas menos preponderantes permiten encontrar la solución numérica. Entre los métodos de resolución se encuentran los métodos hidrológicos, de onda cinemática, onda difusiva, onda dinámica cuasi-permanente. En general los métodos de resolución simplificados se utilizan para modelación hidrológica, ya que las limitaciones en cuanto a capacidad y velocidad de los procesadores actualmente permiten obtener resultados con un gasto computacional reducido y en tiempos relativamente cortos.
El programa HEC-RAS 5.0.3, emplea un método que no considera la viscosidad artificial y se denomina “Local Partial Inertia (LPI)”. Este método consiste en añadir un término a las ecuaciones para reducir los términos de inercia cuando el número de Froude se acerca a la unidad, donde se producirá invariablemente un cambio de régimen en el flujo y se genere una posible discontinuidad. En el método LPI se incluye el factor “Exponent for Froude number reduction factor” conocido como factor “m”. Cuando este valor es igual a la unidad se consigue resultados estables. Un factor de ponderación que se aplica a las ecuaciones en diferencias finitas usadas en el cálculo del régimen variable es el “Theta Weighting Factor”, cuando este valor es cercano a 1.0, se alcanza mayor estabilidad, sin embargo, valores alrededor de 0.6 permitirán disponer de resultados más precisos al realizar la simulación numérica (Hamad, 2008).
Existen varios factores que intervienen en la estabilidad del modelo numérico entre los que se destacan los siguientes:
-
La distancia entre secciones transversales, puesto que a menor distancia entre ellas se alcanza mayor estabilidad con una mayor demanda del tiempo de cálculo.
El intervalo de cálculo (time-step), produciéndose mayor estabilidad numérica a medida que este valor es pequeño a cambio de un elevado tiempo de simulación.
La simulación previa en régimen permanente es una aproximación a la solución final que permite alcanzar estabilidad en el modelo con para flujo no permanente.
4.4 Definición de hidrogramas de crecida
Según Samaniego (2004), dada la duración del evento eruptivo, el hidrograma típico o característico para un lahar inducido por un flujo de lava tendría un inicio lento y probablemente varios pulsos. La erupción volcánica del Cotopaxi ocurrida en el año 1877 fue del tipo explosiva (Mothes, 2004), lo cual conduce a plantear que el volumen de agua sería liberado de forma súbita.
Se plantea que el hidrograma de inicio presenta una forma triangular desfasada, con un pico o valor máximo de crecida y atenuación lenta de manera análoga a los hidrogramas propuestos para el Mount Saint Helens (Brugman & Meier, 1981) y Nevado del Ruíz (Pierson et al., 1990). Se reporta que el evento eruptivo tendría una duración total de 30 minutos (Wolf, 1878), el cual es considerado en la definición de las condiciones iniciales de contorno del modelo numérico.
De esta manera se plantea en la presente investigación que el pico de crecida ocurra en el primer tercio de la duración total del evento, es decir a los 10 minutos del inicio. Se considera que el volumen del agua es función directa del área o superficie del glaciar multiplicada por el espesor o altura de derretimiento, la cual no es generalizada y varía en función del escenario estudiado (CIERHI, 2017).
Considerando que el agua en estado sólido tiende a variar su volumen, se estima un factor de conversión de 0,9 al cambiar al estado líquido. Además, según la reología del lahar se plantea que la mezcla se componga de un tercio de agua y dos tercios de material sólido (volumen de lahar producido será tres veces mayor al volumen de agua). Para el escenario de calibración del flanco Sur del volcán, de los 10 millones de metros cuadrados (m2) de glaciar correspondientes a un volumen total de 40 millones de metros cúbicos (m3), alrededor de 36 millones de m3 constituyen el volumen de agua y 108 millones de m3 representan el volumen de lahar. Al relacionar los volúmenes de lahar con sus correspondientes hidrogramas se obtienen los caudales para cada uno de los cuatros tramos o cauces iniciales de la red de drenaje Sur. Tabla 3
4.5 Calibración del modelo numérico unidimensional
Con base en los vestigios de campo del evento eruptivo histórico de junio de 1877, el cual tiene características similares a un escenario eruptivo tipo 3 (VEI 3-4), se obtiene información acerca de las profundidades de flujo. Estos niveles del flujo son generados mediante la simulación numérica unidimensional empleando la base topográfica digital (Modelo Digital del Terreno MDT) con pixel de tres metros que representa la morfología de la zona de estudio.
En principio se analizan 40 secciones que sirven posteriormente para la calibración de otras 163 secciones transversales aledañas. La distribución espacial en el área de estudio de las secciones transversales utilizadas en la calibración del modelo se muestra en la Figura 5.
Con la modelación numérica del escenario de Calibración, se obtiene los coeficientes de rugosidad (n de Manning) que permiten alcanzar los niveles de flujo obtenidos en el campo.
A partir de la simulación numérica de los cauces iniciales se generan hidrogramas de crecida en los tramos intermedios y final del río Cutuchi. De esta manera se representan las características físicas del evento histórico en toda el área de estudio y se obtienen los coeficientes de resistencia al movimiento que se resumen en la Tabla 4.
5. RESULTADOS DE LA MODELACIÓN NUMÉRICA
Con el análisis de flujo permanente se determina la profundidad y velocidad de flujo, considerando el caudal total en cada tramo. Para el análisis de flujo no permanente (dt¹0) se requiere el uso de hidrogramas de crecida, considerando la variable temporal para obtener resultados orientados a la determinación aproximada y referencial del tiempo de llegada del flujo a una determinada sección.
De acuerdo a lo mencionado en este documento, se cuenta con cuatro escenarios eruptivos que presentan una probabilidad de ocurrencia determinada que está asociada al Índice de explosividad volcánica (VEI).
Para la determinación de los volúmenes de lahar, se requiere conocer las áreas de glaciar y los espesores de derretimiento promedio en cada caso, los mismos que pueden alcanzar hasta 10 metros de profundidad para el escenario 4 (VEI >4) como se muestra en la Tabla 5.
Tabla 5. Coeficientes de rugosidad del modelo numérico calibrado
| Escenario | VEI | Espesor(m) | Volumen Agua(millones de m3) | Volumen Lahar(millones de m3) |
| E1 | 1 – 2 | 1 | 4 | 12 |
| E2 | 2 – 3 | 2 | 8 | 24 |
| E3 | 3 – 4 | 5 | 20 | 60 |
| E4 | > 4 | 10 | 40 | 120 |
Al relacionar los volúmenes de lahar con los tiempos de duración del evento eruptivo se determinan los hidrogramas de crecida y a partir de estos se obtienen los caudales pico o máximos que se alcanzan en el minuto 10 (primer tercio de la duración total) para cada uno de los tramos iniciales. Tabla 6
Tabla 6. Distribución de caudales en (m3/s) por tramo inicial de simulación
| Esc. | Cutuchi | S. Lorenzo | Pucahuaicu | Aláquez | Total |
| E1 | 4 029 | 3 124 | 2 683 | 3 551 | 13 387 |
| E2 | 8 059 | 6 248 | 5 366 | 7 101 | 26 774 |
| E3 | 20 147 | 15 620 | 13 415 | 17 754 | 66 936 |
| E4 | 40 295 | 31 239 | 26 830 | 35 507 | 133 872 |
Los hidrogramas de crecida que se van generando a partir del análisis de flujo no permanente alcanzan valores máximos en tiempos no necesariamente simultáneos pues el modelo numérico considera variables como la longitud, pendiente del cauce, geometría de las secciones transversales y coeficientes de resistencia al movimiento. Se obtienen los mayores resultados de profundidad en los tramos encañonados, como el Aláquez 1, con valores de hasta 40 metros. Sin embargo se observa la reducción de estos valores en las zonas planas o de inundación, como en el tramo Cutuchi 2, en el cual se registran profundidades en el cauce de hasta 8 metros de profundidad.
Para el escenario más probable (E3), las velocidades máximas promedio alcanzan valores de hasta 28 m/s. En la Tabla 7 se reporta los tiempos referenciales correspondientes a la entrada y salida respectivamente, de los tramos de análisis del modelo numérico unidimensional para flujo no permanente.
Tabla 7. Tiempos de llegada en minutos de los caudales máximos
| Tramo | E1 | E2 | E3 | E4 | ||||
| Ent. | Sal. | Ent. | Sal. | Ent. | Sal. | Ent. | Sal. | |
| Cutuchi 1 | 10 | 86 | 10 | 83 | 10 | 71 | 10 | 57 |
| San Lorenzo 1 | 10 | 31 | 10 | 27 | 10 | 24 | 10 | 21 |
| Pucahuaicu 1 | 10 | 26 | 10 | 25 | 10 | 22 | 10 | 21 |
| Aláquez 1 | 10 | 81 | 10 | 66 | 10 | 52 | 10 | 43 |
| Saquimala 1 | 36 | 47 | 26 | 43 | 23 | 37 | 21 | 31 |
| Cutuchi 2 | 47 | 65 | 43 | 62 | 37 | 55 | 31 | 48 |
| Cutuchi 3 | 65 | 206 | 63 | 175 | 54 | 155 | 47 | 144 |
Los tiempos de ocurrencia (llegada) de los caudales máximos (pico) en los hidrogramas a la entrada y salida de cada uno de los tramos de simulación varían en función de cada escenario. Con la modelación numérica se determinan resultados de entre 206 minutos (03:26 horas) y 144 minutos (02:24 horas) correspondientes al tiempo en que el flujo de lahar alcanzaría la salida del tramo Cutuchi 3 para los escenarios 1 y 4 respectivamente.
En la Tabla 8 se presenta los tiempos referenciales asociados a caudales máximos de crecida en varios sitios representativos donde se encuentran zonas pobladas de importancia dentro del área de estudio.
Tabla 8. Tiempos de llegada en minutos de los caudales máximos a varias poblaciones dentro del área de estudio
| Población | E1 | E2 | E3 | E4 |
| Aláquez | 60 | 50 | 40 | 30 |
| Latacunga | 95 | 74 | 64 | 55 |
| Salcedo | 120 | 102 | 94 | 82 |
Los resultados obtenidos en relación a los tiempos de llegada de los flujos de lahar a los sitios representativos de la zona analizada, presentan una variación que guarda relación con la distancia entre el volcán y el lugar de llegada, pero fundamentalmente con el escenario eruptivo. Se observa que conforme se incrementa el escenario eruptivo, la llegada del flujo ocurre en menor tiempo. Para el escenario E3, de acuerdo a lo reportado, se espera que el flujo de lahar alcance la ciudad de Latacunga en aproximadamente 64 minutos.
5.1 Mapas de afectación por el tránsito de lahares primarios
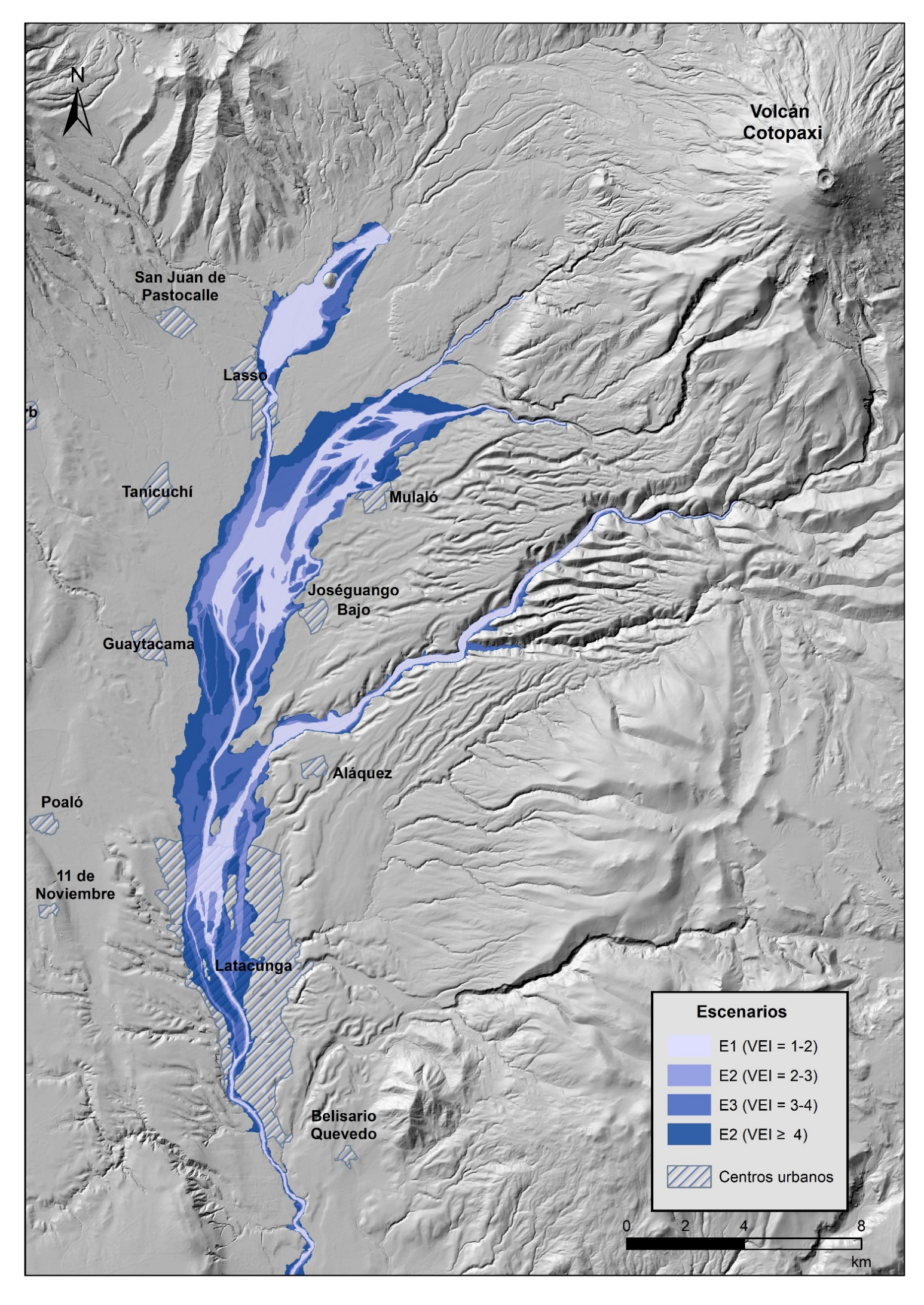
En la Figura 6, se presenta en forma gráfica el área de afectación generada para el escenario de mayor probabilidad de ocurrencia (color celeste) y el Mapa de peligros Cotopaxi Sur IG-EPN (color verde). La primera está en función del modelo numérico para flujo no permanente en base a hidrogramas de crecida de las condiciones actuales del glaciar, mientras que la planteada por el IG-EPN (2016), corresponde al levantamiento de vestigios de campo asociados al evento eruptivo histórico del año 1877 con reconocimiento de los depósitos de flujos piroclásticos y zonas de caída de ceniza.
Con los resultados de la modelación numérica del flujo de lahares primarios en el drenaje Sur-Occidental del volcán Cotopaxi se elaboran Mapas de afectación considerando los cuatro escenarios eruptivos probables.
En la Figura 7 se presentan las zonas de afectación probables dentro del área estudiada que corresponden principalmente a la ciudad de Latacunga, la cual se encuentra asentada en la zona de expansión natural de tránsito del lahar. Cada uno de los escenarios eruptivos analizados generan zonas de afectación que, de manera general tienden a incrementarse conforme aumenta el escenario analizado.
Es importante recalcar que los resultados obtenidos con la modelación numérica permiten establecer zonas de afectación que deben considerarse como aproximadas y si bien no constituyen límites absolutos, son referenciales. Esto debido a la naturaleza del fenómeno natural estudiado en cuanto a su ocurrencia, magnitud, alcance y grado de amenaza.
6. CONCLUSIONES
La simulación numérica unidimensional de flujo permanente y no permanente (variable), es analizada en tramos independientes con la finalidad de alcanzar la convergencia y estabilidad del modelo numérico, en ambos casos se han determinado coeficientes de resistencia al movimiento calibrados en base a los niveles de lahar obtenidos con el trabajo de campo realizado por el IG-EPN relacionado con el evento eruptivo ocurrido en el año 1877.
Los lahares primarios del volcán Cotopaxi tienen características reológicas de flujo hiperconcentrado, granular, no cohesivo similar al flujo dilatante que se puede considerar como turbulento cuando se alcanza valores de caudal unitario superiores a 100 m3/s/m, esta condición hace posible el estudio de este tipo de mezclas utilizando modelos numéricos que, si bien son sencillos y producen resultados aproximados, permiten disponer de información relativamente precisa.
Se asume un comportamiento del lahar como flujo turbulento utilizando el modelo numérico HEC-RAS el mismo que, no permite el análisis de aspectos complejos como mezclas multifásicas, procesos de arrastre y depósito de sedimentos, pero es útil ya que produce resultados de forma relativamente rápida y sencilla. El programa requiere la modificación de los coeficientes de resistencia al movimiento (n de Manning) a fin de alcanzar la calibración del modelo numérico, estos valores varían para este caso particular entre 0,025 y 0,159.
Con los resultados numéricos del escenario de mayor probabilidad de ocurrencia (E3) se determina que la profundidad máxima alcanza 40 metros de altura, la velocidad máxima promedio se encuentra en el orden de 28 m/s y el caudal más alto para este escenario es de 20 147 m3/s. Se determinan tiempos referenciales de llegada o paso del lahar por las poblaciones aledañas más relevantes del área considerada para el estudio en base al análisis de los resultados obtenidos con la modelación numérica para flujo no permanente en la cual se utiliza los hidrogramas de crecida tanto a la entrada como a la salida de los tramos de simulación.
Los mapas de afectación por flujo de lahares primarios del drenaje Sur del volcán Cotopaxi constituyen un aporte técnico significativo puesto que pueden ser usados para tomar decisiones acerca de la definición de sitios seguros, rutas de evacuación e incluso la revisión de la planificación territorial, todo esto sin dejar de lado los planes de concientización, recuperación y mitigación ante los efectos producidos por el paso de lahares ante una eventual erupción volcánica.