1. INTRODUCCIÓN
En los últimos años se ha tenido una necesidad de diversificar las fuentes de generación de energía eléctrica, con lo que se ha impulsado en gran medida las fuentes de generación basadas en energías renovables, entre las más importantes destacan la energía eólica y la fotovoltaica. Para el primer caso, el viento es un recurso limpio e inagotable, disponible en la mayor parte del mundo, aunque no todas con la misma cantidad, pero sí existen zonas específicas en las cuales el recurso natural es cuantioso (Ackermann, 2012).
Existen diferentes métodos estadísticos para calcular la velocidad media del viento, la densidad de energía eólica y el factor de carga de un área geográfica específica (Lubosny, 2003); permitiendo determinar zonas idóneas para instalar parques eólicos que pueden abarcar desde varios MW hasta algunos kW, dependiendo de las necesidades de consumo que se tenga.
Bajo esta perspectiva se busca que los sistemas de conversión de la energía eólica a eléctrica extraigan la mayor cantidad de energía. Para lo cual, los diferentes fabricantes de turbinas eólicas plantean diferentes modelos físicos con la finalidad de extraer la mayor cantidad de energía del viento. Entre las características básicas que se modifican son: el tipo de turbina (eje horizontal o vertical), el número de arpas y el diseño mecánico y aerodinámico, sin embargo, su desempeño no es igual para todo el intervalo de velocidades del viento, ni de la velocidad angular de las aspas (Lubosny, 2003).
Por lo que el presente trabajo se centra en el realizar un estudio comparativo del desempeño de diferentes turbinas eólicas, para establecer la dependencia de su desempeño en relación a los coeficientes de potencia y de par de cada una de ellas. Esto permite conocer con mayor profundidad el comportamiento de cada turbina. Además, permitirá realizar estudios más específicos en relación a algoritmos del seguimiento del punto de máxima potencia en sistema de generación eólica.
2. POTENCIA Y PAR EÓLICO
Para obtener la potencia eólica (Pv) que proporciona una turbina eólica (Lubosny, 2003), (Hau, 2013), (Trevor, 2017) se tiene que la potencia del viento (Pv) se define por la ecuación:
Donde ρ es la densidad del aire, r es el radio del aspa de la turbina y vω es la velocidad del viento.
Sin embargo, la potencia cinética del aire no puede ser convertida al 100% en energía mecánica, debido a que debe cumplir la ecuación de continuidad del flujo de aire, cuando se pasa a través una turbina (Villarrubia, 2013), esto es, el viento al pasar por la turbina se frena, saliendo a una velocidad menor, pero siempre distinta de cero. En una turbina eólica ideal, la velocidad del viento se reduce a un 59.25 %, según la ley de Betz. A este valor se le llama Límite de Betz
Por consiguiente, la potencia en la turbina (Pa) es la potencia eólica que es extrae del viento, con lo que se obtiene una relación entre ambos parámetros, dicha relación se le conoce como coeficiente de potencia (Cp), empleando esta relación se obtiene que la Pa se expresa por:
El Cp depende del tipo de turbina eólica utilizada, del diseño mecánico y la aerodinámica de la turbina, además de la velocidad de angular de la turbina, el ángulo de ataque de las aspas y la velocidad del viento. En un solo tipo de turbina, el comportamiento de Cp depende fundamentalmente de dos factores:
-
De la velocidad específica (Tip speed ration, λ).
Del ángulo de ataque de las aspas de la turbina (β).
Por consiguiente, el coeficiente de potencia está dado en función de dos variables Cpf2 (λ,β). La velocidad específica es la relación entre la velocidad lineal o tangencial del extremo del aspa de la turbina y la velocidad del viento, expresada por:
Donde ωm es la velocidad rotacional de la turbina.
El par en el eje de la turbina eólica (Tm) se calcula mediante:
Sustituyendo la Ecuación (2) en la Ecuación (4) y despejando Tm se obtiene
Considerando la Ecuación (3) y sustituyendo en la Ecuación (5) se obtiene:
De donde se establece que:
Donde Ct es el Coeficiente de par, con lo que la Ecuación (6) se expresa como:
3. COEFICIENTES DE POTENCIA Y DE PAR
El coeficiente de potencia y de par para ser estudiados y analizados, se han expresado mediante modelos matemáticos, los cuales se agrupan en tres funciones:
Debido a que el coeficiente de par depende al de potencia como se expresa en la Ecuación (7), el estudio y análisis se centra en el coeficiente de potencia. Los modelos de Cp basados en una función exponencial y en una función sinusoidal dependen de λ y β, con lo que en estos casos la potencia y el par de la turbina son funciones de la velocidad del viento, de la velocidad de rotación de la turbina y del ángulo de ataque de las aspas. Estos modelos son empleados principalmente en turbinas de mediana y alta potencia, debido que son los esquemas donde se emplea el ajuste del ángulo de las aspas, ya que, en turbinas de baja potencia, se emplean un ángulo constante de ataque del aspa (Moussa et al., 2014). Para los modelos basados en una función polinomial, se considera el ángulo de ataque de las aspas constante, por lo que la potencia y el par solo están en función de la velocidad específica.
3.1 Modelos basados en una función polinomial
Los modelos basados en una función polinomial se rigen en la expresión matemática general propuesta por Li et al. (2007), la cual es expresada por:
Según la literatura, se encontraron cuatro modelos, que se basan en una función polinomial, los cuales tienen distinto orden, el modelo de tercer orden es mostrado por Moussa et al. (2014), el de cuarto orden por Arifujjaman et al. (2016), el de quinto orden por Carranza et al. (2014) y el de séptimo orden por Li et al. (2007). Si la Ecuación (9) se desarrolla considerando el orden más alto del modelo encontrado se obtiene:
Los modelos encontrados varían los coeficientes del polinomio de acuerdo a los valores mostrados en la Tabla 1, la cual se clasifica de acuerdo al orden del polinomio.
3.2 Modelos basados en una función Sinusoidal
En relación a los modelos del coeficiente de potencia que se basan en una función sinusoidal, en la literatura se encuentran cinco diferentes y se clasifican de acuerdo al artículo. El modelo A es mostrado por Moussa et al. (2014), el modelo B por Coto el al. (2014), el modelo C por Xin et al. (2014), el modelo D por Merahi et al. (2014) y el modelo E por Nouira et al. (2012). Analizando cada uno de los modelos se obtiene una función general que cumple con todos los modelos que se relaciona con el comportamiento en base a una función sinusoidal, dicha función general es expresada por:
La Tabla 2 muestra los coeficientes de cada uno de los modelos encontrados, los cuales se aplican en la Ecuación (11), según el modelo asociado al artículo de donde se obtienen dichos parámetros.
Tabla 1. Coeficientes de los diferentes modelos de Cp en función Polinomial
| Coeficiente | 3° | 4° | 5° | 7° |
|---|---|---|---|---|
| a0 | -0.02086 | 0.11 | 0.0344 | 0 |
| a1 | 0.1063 | -0.2 | -0.0864 | 0.00510 |
| a2 | -0.004834 | 0.097 | 0.1168 | -0.0022 |
| a3 | -0.000037 | -0.012 | -0.0484 | 0.0052 |
| a4 | 0 | 0.00044 | 0.00832 | -5.1425x10-4 |
| a5 | 0 | 0 | -0.00048 | -2.7950x10-5 |
| a6 | 0 | 0 | 0 | 4.6313x10-6 |
| a7 | 0 | 0 | 0 | -1.3310x10-7 |
Tabla 2. Coeficientes de los diferentes modelos de Cp en función sinusoidal
| Coef. | Modelo | ||||
| A | B | C | D | E | |
| a0 | 0.5 | 0.44 | 0.44 | 0.5 | 0.5 |
| a1 | -0.00167 | 0 | -0.0167 | -0.0167 | 0.0167 |
| a2 | -2 | 0 | 0 | -2 | -2 |
| a3 | 0.1 | -1.6 | -3 | 0.1 | 0.1 |
| a4 | 18.5 | 15.0 | 15.0 | 10 | 18.5 |
| a5 | -0.3 | 0 | -0.3 | -0.3 | -0.3 |
| a6 | -2.0 | 0 | 0 | 0 | -2.0 |
| a7 | -0.00184 | 0 | -0.00184 | -0.00184 | -0.00184 |
| a8 | -3.0 | 0 | -3.0 | -3.0 | -3.0 |
| a9 | -2.0 | 0 | 0 | -2.0 | -2.0 |
| b0 | 1 | 0 | 1 | 1 | 1 |
| b1 | 1 | 0 | 1 | 1 | 1 |
| b2 | 1 | 0 | 1 | 1 | 1 |
3.3 Modelos basados en una función exponencial
A partir de la revisión documental de los modelos del coeficiente de potencia, se agrupan ocho diferentes modelos que siguen un comportamiento exponencial, de manera que realizando un análisis se obtiene una función general que satisface todos estos modelos, la cual es mostrada por
Donde λi es expresada por:
Los valores de los coeficientes que satisfacen la ecuación (12) se muestran en la Tabla 3, de acuerdo con el modelo de referenciado en la literatura; y los valores de los coeficientes que satisfacen la Ecuación (13) se muestran en la Tabla 4, de igual manera agrupados según el modelo de referenciado en la literatura. Los modelos se relacionados según el artículo de donde son obtenidos como se indica a continuación: el modelo F es propuesto Kotti et al. (2014), el modelo G por Kaur et al. (2012), el modelo H encuentra en varios artículos que son Ovando et al. (2007), Lu et al. (2012), Zhiqiang et al. (2014), Aree et al. (2014); Duman et al. (2014), Hamane et al. (2014) y en Gou et al. (2011), el modelo I se encuentra en varios artículos que son Gao et al. (2008), Bagh et al. (2012), Yin et al. (2007), Shi Q. et al. (2013), Chen et al. (2012) y en Chen et al. (2009), el modelo J es propuesto por Llano et al. (2014), el modelo K es mostrado por Shi B.et al. (2013) y Boukettaya et al. (2014), el modelo L por Bustos et al. (2012) y el modelo M por Ahmed et al. (2014).
Tabla 3. Coeficientes de los diferentes modelos de C_p en función exponencial para la Ecuación (12)
| Coef | Modelo | |||||||
| F | G | H | I | J | K | L | M | |
| c0 | 0.5 | 0.5 | 0.5176 | 0.22 | 0.5 | 0.73 | 0.44 | 1 |
| c1 | 116 | 116 | 116 | 116 | 72.5 | 151 | 124.99 | 110 |
| c2 | -0.4 | -0.4 | -0.4 | -0.4 | -0.4 | -0.58 | -0.4 | -0.4 |
| c3 | 0 | 0 | 0 | 0 | 0 | -0.002 | 0 | -0.002 |
| c4 | - | 0 | 0 | 0 | 0 | 2.14 | - | 2.2 |
| c5 | -5 | -5 | -5 | -5 | -5 | -13.2 | -6.94 | -9.6 |
| c6 | -21 | -21 | -21 | -12.5 | -13.12 | -18.4 | -17.05 | -18.4 |
| c7 | 0 | 0 | 0.0068 | 0 | 0 | 0 | 0 | 0 |
Tabla 4. Coeficientes de los diferentes modelos de Cp en función exponencial para la Ecuación (13)
| Coef. | Modelo | |||||||
| F | G | H | I | J | K | L | M | |
| d0 | 0.08 | 0 | 0.08 | 0.08 | 0.08 | 0.02 | 0.08 | 0.02 |
| d1 | 0 | 0.088 | 0 | 0 | 0 | 0 | 0 | 0 |
| d2 | 0.035 | 0.035 | 0.035 | 0.035 | 0.035 | 0.003 | 0.001 | 0.03 |
4. ANÁLISIS DE LA POTENCIA Y DEL PAR EN LA TURBINA EÓLICA DE ACUERDO A SU MODELO
Una vez analizado los diferentes coeficientes de potencia, según modelos reportados, se procede a analizar el comportamiento de cada uno de los modelos en relación a la potencia y el par que proporcionan cada uno de ellos. El análisis se realiza de forma analística mediante Matlab, bajo las mismas condiciones para todos los casos, las cuales se muestran en la Tabla 5. Además, para analizar la potencia y el par en una turbina eólica se emplean las Ecuaciones (2) y (8) y para calcular la velocidad rotacional de la turbina se emplean la Ecuación (14).
Realizando el análisis de la potencia y del par en una turbina eólica con el coeficiente de potencia basado en una función polinomial, se aplica la Ecuación (10) y los valores de la Tabla 1 y de la Tabla 5, de acuerdo a los modelos encontrados. El comportamiento de potencia para los cuatro modelos polinomiales, se muestran en la Figura 1. El comportamiento del par en el eje de la turbina relacionado a estos mismos modelos se muestra en la Figura 2. En ambos casos se relacionan los comportamientos de la potencia y el par en función de velocidad de giro de la turbina en rpm.
De la Figura 1 se observa que el comportamiento del coeficiente de Potencia es adecuado para los modelos con función polinomial de tercer, quinto y séptimo orden en este rango de velocidades, sin embargo, el comportamiento que presenta el modelo con la función polinomial de cuarto orden no es conveniente, debido a que una vez que baja su nivel vuelve a aumentar para velocidades de giro superiores a 770 rpm, lo cual no sucede en el comportamiento de una turbina real. Este modelo si se puede emplear siempre y cuando acote a una velocidad de giro no mayor a 770 rpm. De la Figura 2 se observa que el par es muy alto a bajas velocidades de giro de la turbina para los modelos que presentan un comportamiento polinomial de tercer y quinto orden, por lo hay que tener en cuenta este parámetro cuando se diseñe un aerogenerador. Con lo que respecta al modelo que tiene una función de cuarto orden, también el par presenta el mismo problema de tiene la potencia, que es que su valor empieza a subir para velocidades de giro superiores a 770 rpm, porque que su empleo solo se recomienda siempre y cuando no se trabaje a velocidades superiores de 770 rpm.
Tabla 5. Parámetros del sistema
| Parámetro | Valor |
|---|---|
| Radio del aspa ( r) | 1.5 m |
| Velocidad del viento (vω) | 10 m/s |
| Velocidad de giro de la turbina (nm) | 100 – 900 rpm |
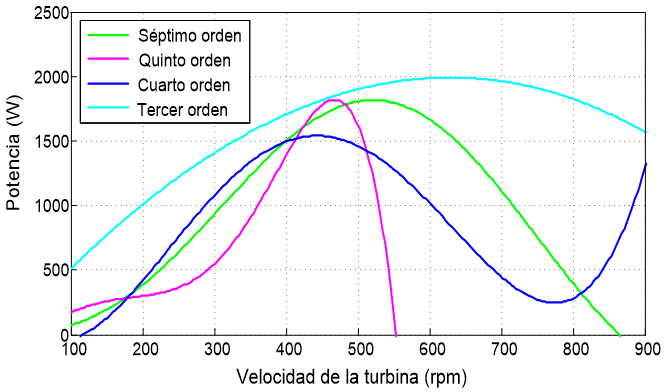
Figura 1. Potencia en la turbina eólica de acuerdo al coeficiente de potencia, según lo modelos matemático basado en un polinomial.
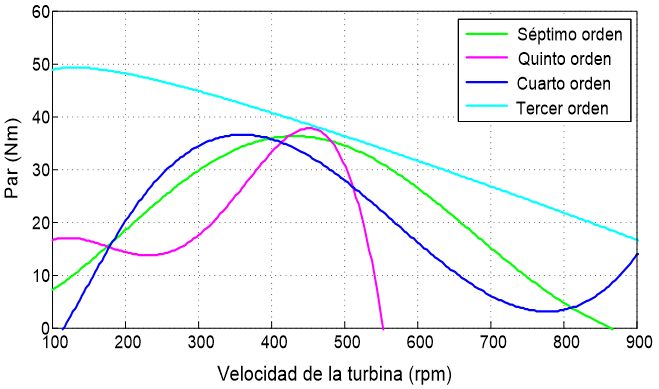
Figura 2. Par en el eje de la turbina eólica de acuerdo al coeficiente de potencia, según lo modelos matemático basado en un polinomial.
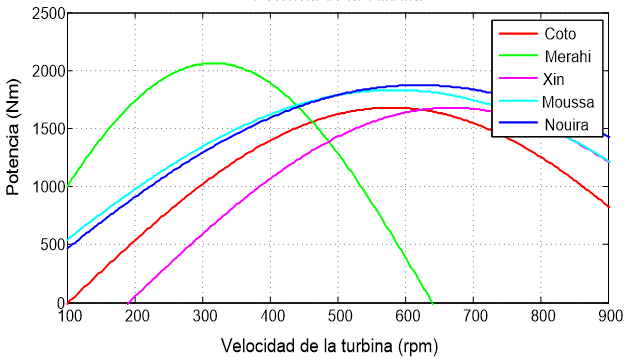
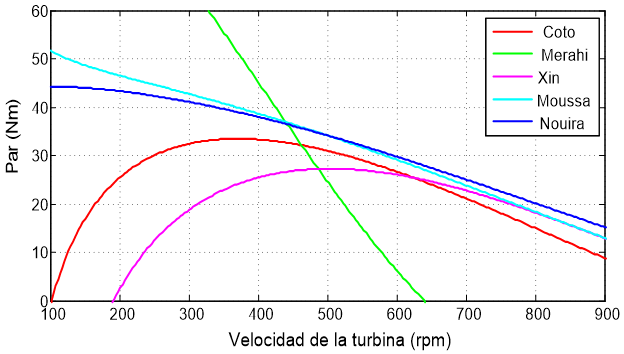
Realizando el análisis de la potencia y del par en una turbina eólica con coeficiente de potencia para los modelos basado en una función sinusoidal, se emplea la Ecuación (11) y los valores de la Tabla 2 y de la Tabla 5. Nuevamente, considerando la velocidad de giro de la turbina, se obtiene el comportamiento de potencia para los cinco modelos sinusoidales, los cuales se muestran en la Figura 3. En la Figura 4 se muestra el comportamiento del par en el eje de la turbina de los mismos cinco modelos que se basan en una función sinusoidal.
De la Figura 3 se observa que la potencia que se obtiene es adecuada cuando se emplean todos los modelos del coeficiente de potencia que siguen un comportamiento sinusoidal, los cuales fueron presentados en la literatura. La diferencia que se establece entre ellos es básicamente de amplitud y del intervalo de velocidades a las que responde. Para el caso del par del eje de la turbina se observa en la figura 4, que los modelos basados en funciones sinusoidales que presenta Coto, Nouira y Moussa tienen un alto valor de par a bajas velocidades de giro de la turbina, por lo que es un parámetro a considerar ampliamente en el diseño del aerogenerador, los otros dos modelos presentan valores no tan altos, por lo que no afectan en el comportamiento del aerogenerador.
Por último, se lleva a cabo el análisis de la potencia y del par en una turbina eólica con coeficiente de potencia mediante un modelo basado en una función exponencial, para lo cual se emplea las Ecuaciones (12) y (13), los valores de los coeficientes de las Tabla 3, 4 y 5. Estos comportamientos nuevamente se obtienen en función de la velocidad de giro de la turbina, se obtiene el comportamiento de la potencia para los ocho modelos exponenciales que se muestran en la Figura 5. Por consiguiente, se muestra el par en el eje de la turbina para los ocho modelos, en la Figura 6.
De la Figura 5 se observa que la potencia de la turbina cuando se analizan los coeficientes de potencia que se basan en una función exponencial, todos tiene un comportamiento adecuado, la diferencia radica entre uno y otro, en la amplitud máxima a que velocidad de giro de la turbina ocurre y a intervalo de velocidades de giro al cual trabajan. De igual manera se observa en la Figura 5 que el par en el eje de la turbina tiene un buen comportamiento como sucede con la Potencia.
5. RESULTADOS
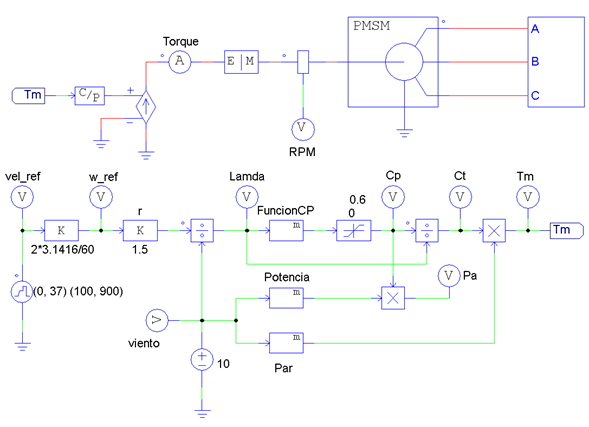
Posteriormente al análisis de la potencia eólica y del par analíticamente, se procede a realizar simulaciones de los diferentes modelos acorde a las funciones matemáticas, de manera que se represente un aerogenerador. Esta simulación se realiza empleando los mismos valores que se emplearon en el análisis matemático con MatLab en la sección anterior (Tabla 5). La simulación se realiza usando la herramienta computacional PSIM, por contar con modelos en su librería que facilitan la representación de las distintas funciones consideradas. La Figura 7 muestra el circuito desarrollado en PSIM, donde se incluye todo el modelo de la turbina eólica. En este circuito es donde se evalúa cada uno de los modelos del coeficiente de potencia que se analizan en este artículo.
En la parte superior de la Figura 7 se está el acoplamiento mecánico de las aspas de con el generador eléctrico. El generador empleado para este caso es el “3-phase permanent magnet synchronous machine with sinusoidal back emf (current-type interface)”, con las siguientes características: 1.5 Ω de resistencia en el estator (Rs), 10 mH en las inductancias del estator en la componente d y q (Ld y Lq), respectivamente, 4 kg∙m2 en el momento de inercia (J) y 4 polos. Para controlar el generador se realiza un acoplamiento eléctrico a mecánico basado en corriente, con lo que se relaciona con el torque que generan las aspas para mover el generador está relacionado a la corriente. Debido a esta dependencia de corriente se emplea una fuente de corriente dependiente de voltaje, con una ganancia unitaria, esto es debido a que el torque se calcula en base a fuentes de voltaje, en la parte inferior de la Figura 7. La carga que se conecta al generador está constituida por la etapa de potencia necesaria para inyectar la energía a la red eléctrica.
En la parte inferior de la Figura 7 se inicia con una fuente de voltaje que permite realizar un barrido de la velocidad del generador de 100 rpm a 900 rpm. Este barrido de la velocidad del generador permite evaluar el comportamiento del aerogenerador dependiendo del coeficiente de la turbina, aplicando en el módulo “FuncionCP” la ecuación (10) y la Tabla 1 para el caso de los modelos polinomiales, la ecuación (11) y la Tabla 2 para el caso de los modelos senoidales y las ecuaciones (12) y (13) y las Tablas 3 y 4, así como, las ecuaciones (2), (3), (7) y (8) requeridas para todo el análisis del comportamiento del aerogenerador.
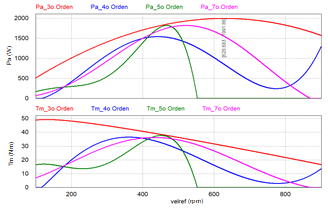
La Figura 8 muestra las curvas de la Potencia (Pa) en la parte superior y del Par (Tm) en la parte inferior, considerando los modelos basados en una función polinomial de 3er orden, 4to orden, 5to orden y 7mo orden. Se observa que el comportamiento es el mismo que se obtuvo en el análisis matemático que se muestra en las Figuras 1 y 2, recalcando nuevamente que el modelo en base a una función polinomial de cuarto orden, no tiene un comportamiento adecuando tanto de potencia como en par, debido a que presenta un incremento de su valor, una ver que ya había bajado, por lo cual, para este modelo se debe de limitar la velocidad de giro de la turbina a 770 rpm. Además, se coincide con el análisis matemático de los modelos de la función polinomial de tercer y quinto orden donde el valor del par a bajas velocidades es alto en comparación con los demás, razón que se debe de considerar para el diseño del aerogenerador.
De acuerdo a los modelos basados en una función sinusoidal, se obtuvieron las curvas de la Potencia (Pa) y del Par (Tm) de los modelos basados en una función sinusoidal, los cuales fueron propuestos por Coto et al., Merahi et al., Noura et al., Moussa et al. y Xin et al. Las curvas se muestran en la Figura 9. De donde se observa que el comportamiento es igual al comportamiento que se obtiene en el análisis matemático mostrado en las Figuras 3 y 4. Llegando a la misma observación, en la cual se establece que la diferencia básica esta en relación a la amplitud máxima obtenida en la potencia y del par y de la velocidad de giro a la que se obtienen estos valores máximos, aunado al intervalo de velocidades de giro que el modelo es útil. En relación al par a bajas velocidades de giro se obtienen también valores altos, los cuales deben ser considerados al momento de diseñar la turbina.
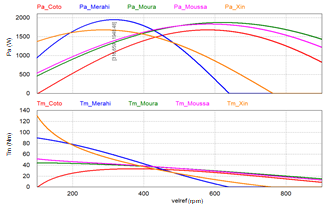
Figura 9. Pa y Tm del modelo sinusoidal propuesto por Coto et al., Moussa et al., Noura et al, Xin et al. y Merahi et al.
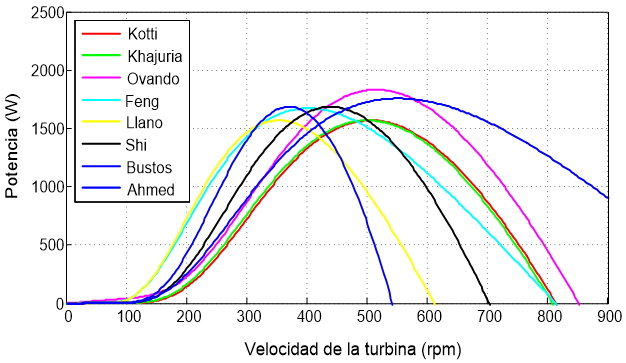
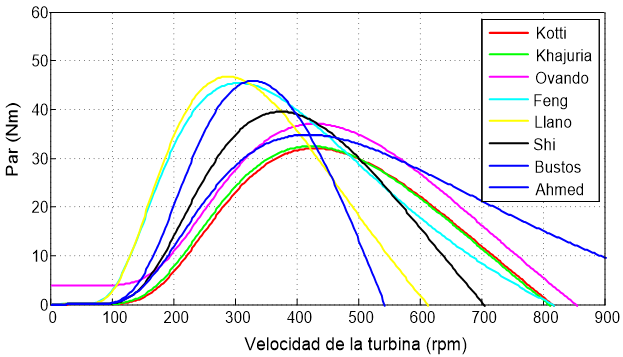
Con respecto a los modelos basados en una función exponencial, la Figura 10 muestra las curvas de la Potencia (Pa) y del Par (Tm) de los modelos propuestos por Aguayo et al., Ahmad et al., Bustos et al., Cai et al., Feng Gao et al., Kaur & Khahuria, Kotti et al. y Llano et al. Realizando una comparación con el análisis matemático de estos modelos mostrados en las Figuras 5 y 6 se observan que son iguales y de la misma manera se observa que la diferencia entre ellos radica principalmente en la amplitud de la potencia y del par y de la velocidad de giro a la que se obtienen estos valores, además, del intervalo de velocidad de giro de la turbina a la cual son válidos.
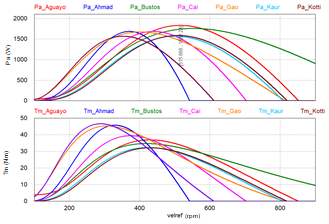
Figura 10. Pa y Tm del modelo exponencial propuesto por Aguayo et al., Bustos et al., Kotti et al., Kaur & Khahuria, Feng Gao et al., Llano et al., Cai et al., y Ahmad et al.
6. DISCUSIÓN
Los modelos basados en una función polinomial dependen únicamente de λ, ya que consideran un ángulo de ataque constante, debido a que estos modelos son empleados principalmente en sistemas de generación eólicas de baja potencia, ya que controlar el ángulo de ataque es muy costoso en relación a la energía que se obtiene. Los modelos exponenciales y sinusoidales dependen tanto del ángulo de ataque de la pala (β) como de la velocidad específica (λ) y se emplean en sistema de generación eólica de mediana y alta potencia.
En los modelos basados en una función sinusoidal, se observa que la potencia (Pa) solo varía su amplitud y en el periodo, esto es, desde que el periodo de velocidad de rotación del eje en rpm (nm) empieza hasta que velocidad termina, por otro lado, como están basados en una función sinusoidal, si se aumenta la velocidad de rotación (nm) considerablemente se genera otra cresta con la misma forma que la inicial, por lo que el sistema debe estar limitado a un intervalo de velocidad de rotación (nm).
En cuanto a los modelos basados en una función exponencial se observa una buena respuesta, debido a que su comportamiento es muy real y se limita automáticamente, por lo que no hay que agregar limitadores el intervalo en el que trabaje en función a la velocidad de rotación (nm).
Realizando un análisis en lo particular de cada uno de los tres modelos generales, se tiene que de los cuatro modelos encontrados que obedecen a una función polinomial, el que presenta el máximo valor de Potencia en la turbina (Pamax ) es el modelo de tercer orden, con un valor de 1.991 kW a una velocidad de giro de 628.68 rpm y tiene una respuesta que representa un comportamiento real (Figura 8 superior, gráfica de color rojo), al igual que el modelo de quinto y séptimo orden (Figura 8 superior, gráfica en verde y magenta, respectivamente). Esta consideración se establece, debido a que no vuelven a crecer después de una determinada velocidad de rotación, como si lo hace el modelo de cuarto orden (Figura 8 superior, gráfica azul); por lo que este modelo es el que presenta una mayor desventaja para su aplicación en modelos reales.
Considerando los cinco modelos que obedecen a una función basada en una sinusoidal, el que presenta el máximo valor de Potencia (Pamax ) es el modelo de Merahi et al., ya que su valor máximo es de 1.948 kW a una velocidad de rotación de 316.65 rpm (Figura 9 superior, gráfica azul). Cabe destacar que todos los modelos siguen el mismo comportamiento, de manera que la potencia se difiere de una en otra, solo en la amplitud y el periodo y no en la forma de tiene la curva de la potencia, como si lo hacen los modelos basados en funciones polinomiales.
De los ocho modelos que siguen un comportamiento exponencial, el que presenta el máximo valor de Potencia (Pamax ) es el modelo de Aguayo et al., ya que su valor máximo es de 1.832 kW a una velocidad de rotación de 515.66 rpm (Figura 10 superior, gráfica roja). A diferencia de los modelos basados en una función polinomial o en una función sinusoidal, todos los modelos basados en una función exponencial tienen un adecuado comportamiento en la Potencia de la turbina y de su par, debido a que todos inician en valores cercanos a cero.
Al concluir las simulaciones del sistema de potencia completo, implementando los todos los modelos basados en funciones polinomiales, sinusoidales y exponenciales; se dedujo que:
-
Dentro de los modelos polinomiales, el modelo de 4to orden registró una incongruencia, ya que la curva característica de potencia tras llegar a su punto máximo como se observa en la Figura 8, describe un comportamiento anormal, al no reducirse gradualmente a cero con el incremento de la velocidad; de hecho, la potencia continúa aumentando lo cual no ocurre en las turbinas eólicas reales.
Al analizar el comportamiento del par en el eje de la turbina en los sistemas de potencia, se observa que en algunos casos el par es muy grande, específicamente superior a 100 Nm. Tal magnitud incidiría desfavorablemente en el diseño del sistema mecánico (radio de las palas y en la relación de transformación de la caja multiplicadora), en una turbina de viento implantada con máquinas eléctricas de baja potencia a la considerada en los ensayos (2kW). Bajo tal circunstancia, se requiere tener en un sistema real limitadores para controlar que no se genere un par muy grande.
Por otro lado, en los modelos sinusoidales, la ecuación matemática no describe el comportamiento real del modelo, sino que se debe de acotar la velocidad de rotación, para evitar variaciones después de un determinado intervalo de velocidades del generador.
Finalmente, se observa en la Figura 10, que los modelos basados en una función exponencial describen de mejor manera el comportamiento de la potencia y el par en el eje de la turbina eólica.
7. CONCLUSIONES
A partir de la revisión documental realizada para hacer el estudio comparativo del desempeño de las turbinas eólicas en relación a su coeficiente de potencia y de par en diferentes turbinas eólicas, se encontró que la diferencia entre cada uno de ellos, depende del coeficiente de potencia y de par que se establece, ya que se pueden tener las mismas características físicas, como son radio de las palas, número de palas, ángulo de ataque, paro si cualquiera de uno de los varia, cambia el comportamiento de la turbina eólica. Dichos coeficientes dependen básicamente de tres modelos matemáticos basados cada uno de ellos en una función específica (polinomial, sinusoidal o exponencial). En este artículo se clasificaron de acuerdo a estas funciones; y en el caso de los modelos basados en una función sinusoidal y exponencial se obtuvo una ecuación general. De acorde a las ecuaciones generales de los modelos, se establece las Tablas 1, 2, 3 y 4 que establecen los coeficientes para cada modelo analizado y se agrupan según su modelo matemático. El análisis del comportamiento de la potencia y del par se realiza de manera analítica mediante el uso de Matlab y se corrobora mediante simulaciones realizadas con PSIM, empleando los mismos parámetros para hacer un análisis comparativo adecuado.
Para el caso de los modelos basados en función sinusoidal y exponencial se considera constante el ángulo de ataque a las aspas. De dichos ensayos, se concluye que tanto el análisis analítico de Matlab y el simulado de PSIM son compatibles. Además, los modelos basados en una función exponencial son los que representan el comportamiento real en todos los casos estudiados. De la misma manera, se logra el comportamiento usando el modelo basado en una función polinomial de séptimo orden. En el caso de los modelos sinusoidales, se debe de acotar el intervalo de velocidades para dar un comportamiento real en lo que corresponde a la potencia, no siendo favorable por los registros de alto par a bajas velocidades; condición que se extiende también, al resto de los modelos basados en funciones polinomiales.
Este análisis es la base para la construcción de un emulador de una turbina eólica que emplee diversos modelos de turbinas de acorde a su coeficiente de potencia y de par, además de los parámetros propios de la turbina; Esto es debido a que esta análisis permite conocer diversos modelos de marera que estos sean introducidos al emulador y que además se permita el cambio de los coeficientes de los modelos de acuerdo a la función que se establezca, para que se puedan evaluar nuevas turbinas que se construyan o se reporte. Este emulador se desea construir para tener una herramienta que permita evaluar diversos sistemas de generación eólica, así como, los algoritmos de búsqueda del punto de máxima potencia.
Los resultados expuestos serán de utilidad para escalar la plataforma a diseñar, tomando en consideración los registros más, acertados de par y de potencia. Estos parámetros son fundamentales para la elección del generador a impulsar, el cual deberá estar acoplado mecánicamente a un motor controlado por un accionamiento electrónico. Bajo tal circunstancia, no es relevante los aspectos limitantes como el radio de las turbinas, la relación de la caja multiplicadora, el control de posicionamiento de las palas, etc.