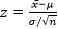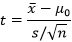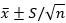I. INTRODUCCIÓN
Es conocida la sensibilidad que tiene la media aritmética ante la presencia de datos atípicos, y por tanto las dificultades que podrían presentarse si confiamos en esta medida como un resumen del centro de la información 1,2. Al menos, en una descripción numérica, este problema parece quedar solucionado cuando se usa la mediana en su lugar, puesto que fácilmente se puede verificar que esta medida permanece robusta ante la presencia de datos extremos 3. Sin embargo, nos preguntamos si la sensibilidad que presenta la media ante estas observaciones, cuando se usa esta medida como un descriptor se mantiene cuando se la usa como un estimador de la media poblacional µ. Como sabemos, en el proceso de inferencia, cuando la varianza teórica es desconocida se usa la prueba t-Student para realizar inferencias sobre µ, por lo que pondremos especial atención en este test de hipótesis 4.
Estudios realizados revelan que la presencia de datos atípicos en una muestra altera la probabilidad de cometer un error tipo I (TIEP por sus siglas en inglés) y disminuye la potencia de test de hipótesis usados para contrastar medias 5,6,7. Algunos coinciden en señalar que estas afectaciones se dan exclusivamente en los test paramétricos (t-Student, F), mientras que para los métodos no paramétricos (Wilcoxon 8, Kruskal-Wallis 9) no existe ningún tipo de afectación, por lo que se cree que las anomalías y la presencia de atípicos no tiene ningún efecto sobre los test de distribución libre 10,11,12,13,14. Sin embargo, estudios posteriores indican que la afectación está presente tanto para pruebas paramétricas como no paramétricas, es decir ambos métodos son sensibles a la presencia de datos atípicos, aunque se aclara que el grado de afectación no es el mismo 15.
Es importante mencionar que estos y otros autores han usado como metodología para generar (simular) datos con valores atípicos el modelo de distribución normal mixta 10,16, el cual consiste en generar un conjunto de datos de dos o más distribuciones normales con distintos parámetros, sobre todo distinta varianza, esto hace que se produzcan datos con desviaciones extremas, los cuales son considerados como atípicos.
A nuestro parecer, esta metodología descrita para generar datos atípicos no es la más adecuada. El problema es que, al mezclar dos distribuciones normales, no se puede garantizar que el nuevo conjunto de datos generados también provenga de una distribución gaussiana, de hecho, al realizar cualquier prueba de hipótesis de normalidad sobre este nuevo conjunto de datos, esta se termina rechazando. Por este motivo, creemos que las investigaciones anteriores muestran una alteración en la TIEP y potencia de las pruebas paramétricas, que no se debe precisamente a la presencia de datos atípicos, sino a la violación del supuesto de normalidad bajo el cual están elaboradas estas pruebas. Por otro lado, esta afectación desaparece cuando se usan test no paramétricos, pero de acuerdo a la analogía planteada, esto podría ocurrir debido a que estas metodologías son diseñadas para datos no normales, que precisamente, son los que se forman al mezclar dos distribuciones normales.
En el presente trabajo, mediante un algoritmo de simulación y usando muestras que presentan datos atípicos, se estima la TIEP y potencia (Complemento de la Probabilidad de error tipo II) de la t-student para inferir sobre una media.
Es necesario estimar la TIEP con el fin de conocer la robustez de la prueba, esto a partir del criterio de Cochran que establece que un test de hipótesis es considerado útil o preciso si la TIEP estimada en el proceso tiene una desviación respecto al nivel de significancia α de máximo el 20% de su valor, es decir si se ubica dentro del intervalo ;(α ±0.2); 17. En esencia, este mismo criterio es usado para establecer si una prueba de hipótesis es robusta 18,19,20.
Las muestras que se usarán para el cálculo de la TIEP, por un lado, serán generadas usando la metodología de distribución normal mixta usada en investigaciones previas, y además generaremos muestras con atípicos que se formen a partir de una sola distribución normal sin necesidad de ningún tipo de contaminación.
Luego, estas metodologías serán comparables y se podrá determinar si la alteración de los errores tipo I y tipo II persisten, aun cuando no se mezclen distribuciones para la generación de la muestra. Finalmente, se realiza una estimación por intervalos de confianza de la media µ en los escenarios propuestos con el fin de observar si existe una variación significativa de este parámetro.
II. MATERIALES Y MÉTODOS
Revisión y comentario de la prueba t - student
Es importante realizar una revisión de la literatura sobre el uso de la prueba t-Student para inferencias sobre la media µ, esto debido a que en el análisis clásico suele existir cierta confusión, sobre todo en lo que respecta a las condiciones que deben tener las muestras en su distribución y tamaño para que sea válido su uso.
La condición más importante para usar una prueba t-Student, es que los datos con los que se trabajan deben provenir de una distribución normal. Por el teorema del límite central 21, conocemos que cuando es la media de una muestra aleatoria (proveniente de cualquier distribución no normal) de tamaño n, entonces la forma límite de la distribución de
conforme n→∞ es la distribución normal estándar N(0,1), es por ello que un posible test de hipótesis para inferencia sobre µ es el que se basa en el estadístico z, determinado por el teorema precedente. Esta aproximación resulta ser buena cuando n≥30, pero note que esto solo si la muestra aleatoria no proviene de una distribución normal, puesto que, si estos datos sí son normales, la media será también lo será, independiente del tamaño de la muestra, es decir para cualquier n mayor o menor que 30.
Por otra parte, note que el estadístico z contiene los parámetros μ y σ, los cuales sabemos que en la realidad son valores desconocidos. En un test de hipótesis, no habría problema por el valor de μ puesto que este sería el valor hipotético sobre el cual se está realizando la inferencia, pero esto no ocurre con el valor de σ, el cual será un valor que a partir de datos reales nunca se conocerá. Es por ello que se utiliza la distribución t-Student como una forma limitante de la normal z cuando no se conoce la varianza poblacional σ2 pero se la puede aproximar a través de la varianza muestral S2 4.
Este análisis nos lleva entonces a la conclusión de que independientemente del tamaño de la muestra (n≥30 o n<30), la única condición para elegir entre una prueba z o una t-Student (siempre y cuando los datos de la muestra provengan de una distribución normal), es el conocimiento o no de la varianza poblacional. En el presente trabajo ponemos énfasis solo en la t-Student puesto que, como ya habíamos mencionado, en un análisis de datos real el valor de σ2 siempre será un parámetro desconocido al cual solo tendremos la oportunidad de estimarlo.
Como ilustración didáctica, a continuación, planteamos el test de hipótesis al que estamos haciendo referencia:
H0: μ=μ0
H1: μ≠μ0 (2)
Rechazaremos H0 si el estadístico de prueba t es mayor que el valor crítico |tα/2|, donde α es el nivel de significancia de la prueba, y t viene dado por:
Que sigue una distribución t-Student con n-1 grados de libertad.
Generación aleatoria de muestras con atípicos
Para la generación de muestras contaminadas, usaremos la metodología del estudio previo, propuesta por Zimmerman 15. Esta consiste en generar muestras provenientes de una normal N(0,1) con probabilidad de ocurrencia 1-p, mezclados aleatoriamente con los de otra distribución normal N(0,k2) con probabilidad p, donde k es una constante que determina el nivel de alejamiento de los atípicos y p determina el porcentaje de datos contaminados en la muestra. En nuestro caso, usaremos los valores de k=20 y p=0.16, que son los valores que usa el autor en su publicación.
Para el caso de muestras no contaminadas, una simulación previa de muestras aleatorias normales N (0,1) mostró que con cierta frecuencia se presentan datos atípicos en ciertos porcentajes de las réplicas generadas, esto independientemente del tamaño de la muestra, por tanto, sin necesidad de mezclas, generamos varias réplicas de una sola distribución normal y separamos aquellas que presenten atípicos. Con la ayuda del software estadístico R (22) y algunos paquetes complementarios 23,24, se crearon funciones y algoritmos de simulación, los cuales generaron 10000000 (diez millones) de muestras N(0,1) de diferente tamaño (n=5,10,20,40), luego con el uso de la función nout (Anexo 1), las separamos, clasificándolas de acuerdo al número de atípicos que se produjeron (0,1,2,…).
El criterio que hemos usado para considerar a un dato extremo es el “Criterio de las vallas de Tukey”, el cual es utilizado por la gran mayoría de software estadístico y determina que un dato se considera atípico si está fuera del intervalo Q1-1.5(Q3-Q1 ), Q3+1.5(Q3-Q1); (25). La Tabla 1 muestra el número de muestras generadas de acuerdo al número de atípicos producidos aleatoriamente en cada una de ellas. Con el fin de que la estimación sea representativa, solo hemos tomado en cuenta los casos en que se han generado más de 10000 (diez mil) muestras.
Estimación de la tiep y potencia
La función creada para estimar la probabilidad de error tipo I y la potencia tiene por nombre tiep (Anexo 1), entre sus argumentos tenemos “nsim” la cual determina el número de muestras totales a generarse (en nuestro caso 10000000); “n” que indica el tamaño de cada una de las muestras (en nuestro caso n=5,10,20,40); “mean” que determina el valor teórico de la media poblacional con las que se generarán las muestras (en nuestro caso 0 y 1 para la TIEP y potencia respectivamente), “alpha” que determina el nivel de significancia (que en todos los casos hemos usado α=0.05), “sd” que siempre será igual a 1, "sdContamin" que tomará el valor de 1 si no queremos contaminar la muestra, o el valor de k2=202 y finalmente "p" que tomará el valor 0 para muestras no contaminadas y 0.16 para contaminar el 16% de la muestra.
Una vez generadas y clasificadas (de acuerdo al número de atípicos) las 10000000 de muestras, con el uso de la función tcal (Anexo 1) determinamos para cada una de ellas el estadístico t, asumiendo siempre una media hipotética igual a cero. El algoritmo cuenta el número de veces que la hipótesis nula es rechazada y divide este valor para el número total de muestras generadas en el caso atípico correspondiente. Esta razón nos entrega una proporción, la cual en el caso de generar muestras de media teórica μ=0 es la proporción de veces que se rechaza la hipótesis nula cuando esta es verdadera (media teórica igual a media hipotética), lo cual resulta ser un estimador de la TIEP. Por otro lado, cuando la media teórica es distinta de cero (en nuestro caso usamos μ=1), la razón representa la proporción de veces que se rechaza la hipótesis nula cuando esta es falsa, lo cual claramente es un estimador de la potencia de la prueba.
Intervalos de confianza para la media
Para todos los escenarios generados, se toma una muestra y se calcula un intervalo de confianza para la media, basada en una distribución t - student, es decir:
Este proceso está implícito dentro de la función tiep (Anexo 1). Los intervalos de confianza permitirán determinar si existe una variación significativa en la estimación de la media para las distintas muestras (contaminadas y sin contaminar), número de atípicos y tamaños muestrales.
III. RESULTADOS
La cantidad de atípicos en cada muestra, depende del número de datos que esta contiene, por ejemplo, para una n=5, el máximo de atípicos obtenidos es 2, lo cual no necesariamente representa una cantidad baja, puesto que constituye el 40% de la información. Así mismo, para un tamaño muestral n=10 se obtuvo un máximo de 4 atípicos, para n=20 un máximo de 5 y para n=40 un máximo de 6. En realidad, aleatoriamente se generan más atípicos (de manera proporcional al tamaño de la muestra), sin embargo, se tomaron solo aquellas muestras que fueron significativamente altas para un proceso de simulación (10000), con el fin de que no exista un elevado error de estimación. La Figura 1 muestra la frecuencia (en millones) del número de atípicos generados en el proceso de simulación para los distintos tamaños muestrales, donde se puede observar claramente que a partir de 6 atípicos generados, el tamaño de la muestra es prácticamente irrelevante. Además, como era de esperarse, se observa que la prevalencia de atípicos es mayor para datos contaminados que para no contaminados.
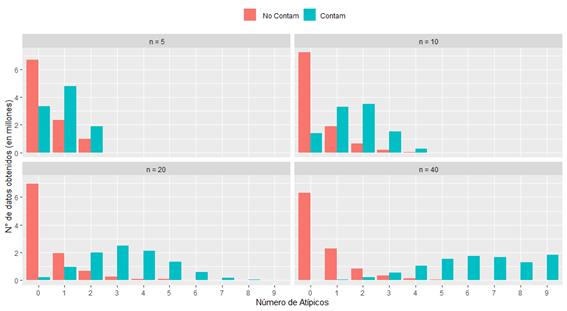
Figura1 Cantidad de datos obtenidos (en millones) en el proceso de simulación para distinto número de atípicos en muestras contaminadas y no contaminadas
La Figura 2, muestra la estimación de la probabilidad de error tipo I (TIEP), calculada como la proporción de veces que se rechaza la hipótesis nula (H0: μ=0) cuando teóricamente esta es cierta. En el caso de muestras no contaminadas se puede observar que, en todos los casos, la estimación es muy cercana al nivel de significancia α=0.05, a excepción de pequeñas desviaciones irrelevantes (de acuerdo al criterio de Cochran) que ocurren principalmente cuando el número de atípicos aumenta. Contrario a esto cuando se contamina la muestra existe una clara alteración de la TIEP por debajo del nivel de significancia.
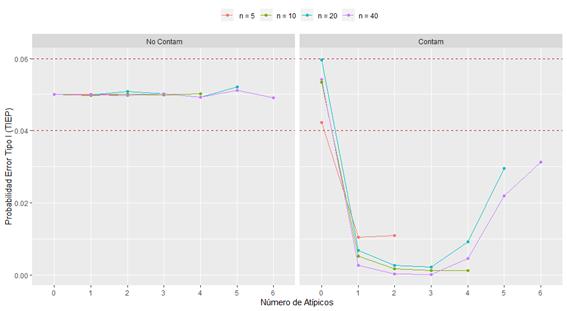
Figura2 Estimación de la TIEP para distintos tamaños muestrales, con α=0.05 en muestras contaminadas y no contaminadas
La Figura 3 muestra la estimación de la potencia calculada como la proporción de veces que se rechaza H0 cuando teóricamente esta es falsa (t-student generado para probar μ=0 mientras que las muestras se generaron con media teórica μ=1). En muestras no contaminadas se observa que la potencia de la prueba solo está afectada por el tamaño de la muestra (entre más grande mayor potencia), y no por la cantidad de atípicos, esto ya que la medida es significativamente la misma tanto en ausencia de valores atípicos como en presencia del máximo de ellos. Por su parte, para muestras contaminadas se observa una potencia demasiado baja, la cual es peor conforme el número de atípicos aumenta.
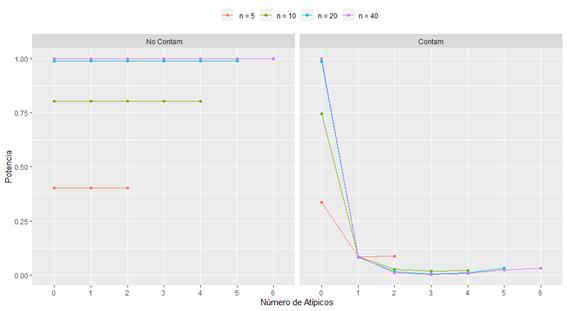
Figura3. Estimación de la Potencia para distintos tamaños muestrales con α=0.05, en muestras contaminadas y no contaminadas.
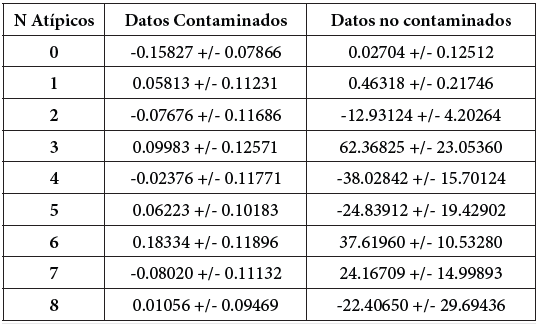
Finalmente, la Tabla 1 muestra intervalos de confianza para la media, calculados para un tamaño muestral n=20. Para datos contaminados, los resultados muestran que las estimaciones no presentan variaciones significativas y que además no se equivocan (contienen el cero) independientemente del número de atípicos que se presenten en la muestra. Para datos no contaminados se observa todo lo contrario, es decir existe variación significativa de los estimadores y además la mayoría de veces se comete un error (el intervalo no contiene el cero). Los errores de estimación en todos los casos, como es normal, son proporcionales al tamaño de la muestra y el mismo comportamiento se observa en los diferentes tamaños muestrales, por lo que se omite la presentación de estos resultados.
IV. DISCUSIÓN
Los resultados obtenidos muestran que cuando existe contaminación de la muestra producida por el método de distribuciones mixtas, la probabilidad de cometer un error tipo I y la potencia de la t - Student se ve alterada de manera significativa, lo cual la hace una prueba poco confiable, no robusta y con una baja potencia.
Contrario a esto, cuando no existe esta contaminación se observa que la cantidad de atípicos que se producen de manera natural en muestras normales no afectan la probabilidad de error tipo I ni la potencia. Estas probabilidades parecen mantenerse estables independientemente de si existen o no cualquier cantidad de datos extremos.
En este punto, obtenemos resultados diferentes a los mencionados en estudios previos, suponemos que estas diferencias se deben a la distinta metodología usada para obtener muestras con datos atípicos.
Los estudios previos usan mezclas de distribuciones normales con una diferencia en sus desviaciones con el fin de obtener los datos extremos, esto parece ser una buena idea, sin embargo, no olvidemos de que, al mezclar dos normales, el resultado deja de ser una normal, con lo cual, al usar estos datos en la prueba t-student estamos faltando con el principal supuesto sobre el cual está elaborada esta prueba.
De nuestra parte no hemos contaminado ninguna distribución, hemos generado aleatorios de una misma normal, para posteriormente separar las muestras de acuerdo al número de aleatorios que se forman (0, 1, 2, …) de manera natural, es decir, esperando que la misma aleatoriedad de la distribución gaussiana cree estos atípicos, con lo cual no estamos afectando el supuesto de normalidad, indispensable para utilizar la t-Student.
Código:
V. CONCLUSIONES
A partir de la metodología implementada en el presente trabajo y de acuerdo al criterio de Cochran, se puede observar que para casos de muestras contaminadas la prueba t -Student no es una prueba robusta ya que no controla el error tipo I y que la potencia es muy baja, haciendo en estos casos que la prueba sea prácticamente inservible.
Esta conclusión no hace más que comprobar los resultados de los estudios previos descritos en el apartado I del presente trabajo.
En el aporte propio de esta investigación, es decir en los casos que usamos muestras con datos atípicos sin necesidad de contaminar o mezclar la distribución normal, se observa que los valores estimados para la TIEP, se encuentran todos dentro del intervalo ; (α ±0.2α) ; (0.04-0.06), de hecho todos son muy cercanos al nivel de significancia α, lo cual nos muestra evidencia para concluir que la prueba t-Student se mantiene robusta ante la presencia de datos atípicos y tiene una potencia alta independientemente de la cantidad de atípicos que tiene la muestra. La diferencia en la potencia solo depende del tamaño muestral, es decir a mayor tamaño, mayor potencia, pero esto no es algo que se produzca por la presencia de atípicos, sino que es una propiedad de la t-Student y en general de todas las pruebas de inferencia estadística