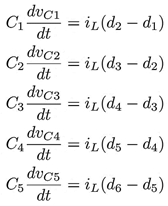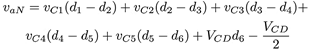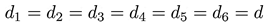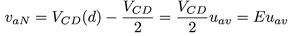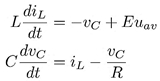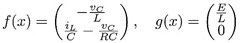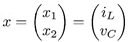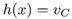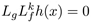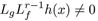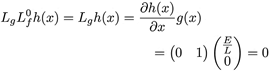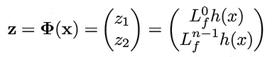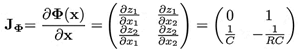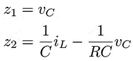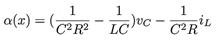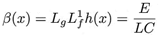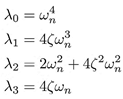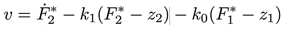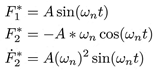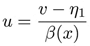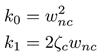Forma sugerida de citación: Aguilar-López, B. A.; Juárez-Abad, J. A.; Barahona-Avalos, J. L.; Mayoral-Lagunes, R.; Linares-Flores, J. y Contreras-Ordaz, M. A. (2020). «Control para el voltaje de salida de un inversor multinivel de capacitores flotantes». Ingenius. N.◦ 24, (julio-diciembre). pp. 68-80. doi: https://doi.org/10.17163/ings.n24.2020.07.
1. Introducción
La energía eléctrica puede presentarse en dos modalidades: de corriente directa (CD) o de corriente alterna (CA). Existen aplicaciones donde se requiere la transformación de una forma de energía a otra, dicha conversión es llevada a cabo por un dispositivo conocido como convertidor de potencia; por ejemplo, la transformación CA-CD la realiza un convertidor llamado rectificador y para el caso de la conversión CD-CA la realiza un convertidor llamado inversor [1]. Los convertidores de potencia se construyen con dispositivos de conmutación y con elementos pasivos tales como capacitores, inductores, diodos y transformadores. Generalmente, la potencia, que es capaz de entregar un convertidor, está limitada por la capacidad de corriente y voltaje de sus interruptores o dispositivos de conmutación. Aún cuando idealmente un inversor debería producir una tensión sinusoidal en las aplicaciones tradicionales de corriente alterna (para lograr mejor eficiencia y baja interferencia electromagnética, entre otras ventajas [2]), estos solo son capaces de producir ondas rectangulares (es decir, tres niveles). Con el surgimiento de las topologías de inversores multinivel, fue posible generar formas de onda de voltaje con múltiples niveles, las cuales se asemejan más a la forma de onda sinusoidal ideal. Las topologías más conocidas de convertidores multinivel son: celdas en cascada, diodos de enclavamiento y capacitores flotantes [3].
La primera topología mencionada se compone de la conexión en serie de puentes H y requiere fuentes de voltaje aisladas para cada una de las celdas, mientras que las dos últimas, ocupan solo una fuente de voltaje [4]. La topología de convertidores multinivel de capacitores flotantes (CMCF) ha demostrado ser una excelente elección en aplicaciones donde se requiere alta densidad de potencia [5]. La estructura de un CMCF está conformada por celdas de potencia. Cada celda de potencia se compone por un par de interruptores y un capacitor flotante. El número de niveles en la salida del CMCF puede incrementarse añadiendo más celdas al CMCF, sin embargo, se requieren más capacitores e interruptores. Cada capacitor flotante debe ser cargado a un voltaje nominal de cierto nivel. Dependiendo del estado de los interruptores de la celda, el capacitor flotante, aportará o no, su voltaje a la salida del convertidor. Para la operación correcta del CMCF se debe mantener una distribución balanceada en los voltajes de los capacitores flotantes: cada uno de ellos debe mantener un voltaje nominal equivalente a una fracción del voltaje total del bus de CD dividido entre el número de celdas. Para lograr la operación correcta del CMCF se realizan dos procesos independientes conocidos como precarga y balanceo (o regulación) de los voltajes en los capacitores flotantes. Para el caso de la precarga, algunos métodos reportados pueden ser consultados en [6] y [7].
Por otra parte, el balanceo de los voltajes en los capacitores flotantes puede realizarse de manera pasiva y activa. El balanceo natural o pasivo utiliza una técnica de modulación, comúnmente llamada como PS-PWM (por sus siglas en inglés, Phase Shifted-PWM). Esta técnica de modulación se emplea para generar los estados de conmutación que forman la señal de voltaje deseado en la salida y al mismo tiempo, mantiene en los capacitores flotantes una carga neta promedio igual a cero. La técnica de balanceo pasivo, mencionada es sencilla de implementar, sin embargo no garantiza que los voltajes de los capacitores se establezcan en sus valores nominales, ya que regularmente los componentes utilizados en la construcción del CMCF poseen condiciones no ideales, es decir: corrientes de fuga desiguales en los capacitores, carga o descarga asimétrica en los capacitores y perturbaciones de carga, por mencionar algunos [8]. Por otro lado, en el balanceo activo, el voltaje de los capacitores flotantes es regulado individualmente. Este enfoque requiere el uso de un sensor de voltaje para cada uno de los capacitores flotantes como se muestra en [9] y [10] o bien, su estimación mediante observadores como se trata en [11]. Una tarea de control necesaria en los convertidores de potencia es proporcionar una salida de voltaje sin cambio en la amplitud, sin importar la resistencia efectiva de la carga. Para el caso del convertidor CD-CA se desea que la salida siga una referencia de voltaje a pesar de las perturbaciones generadas cuando la corriente de carga o del voltaje de entrada cambian [12].
Para que estas tareas sean llevadas a cabo de manera precisa, se requiere un sistema de control con retroalimentación. El seguimiento de voltaje en inversores multinivel ha sido abordado mediante diversas técnicas de control. Para la topología de celdas en cascada, han sido empleados diversos esquemas de control, tales como: controlador basado en pasividad [13] y el control integral proporcional generalizado lineal [14]. Para la topología de capacitores flotantes, el seguimiento de voltaje se ha realizado en [15] y [16]. En [15] se genera cada estado de conmutación apropiado para generar el voltaje de salida deseado, mediante un algoritmo que no requiere una modulación adicional ni el modelo del convertidor. En [16], los autores sostienen que las tareas de balanceo de voltajes y de seguimiento de la referencia de voltaje se encuentran acopladas, lo que se vuelve un problema serio en aplicaciones de alto ancho de banda y alta precisión. Hacen énfasis en el desacoplamiento de dichas tareas mediante dos técnicas: linealización por retroalimentación y una variante de modulación de espacio vectorial. Aplican controladores de tipo proporcional-integral (PI) y regulador cuadrático lineal (LQR) para el seguimiento de voltaje y simples controles proporcionales (P) para el balanceo de los voltajes en los capacitores. El objetivo del presente trabajo es el control por seguimiento de una señal de referencia sinusoidal aplicado al voltaje de salida de un CMCF. La tarea del balanceo de los voltajes en los capacitores flotantes se delega a la modulación PS-PWM. Con ello se evita el uso de múltiples sensores de voltaje y se reduce la complejidad del modelo dinámico del convertidor así como la complejidad en la implementación del controlador.
El controlador está basado en la técnica de rechazo activo de perturbaciones (ADRC, por sus siglas en inglés, Active Disturbance Rejection Control). En la sección 2.1 se describen las partes que componen al sistema: controlador, modulador y el convertidor de potencia. En la sección 2.2 se obtiene el modelo dinámico en forma promedio del CMCF. En la sección 2.3 se realiza la linealización en forma exacta del modelo del CMCF. El diseño del controlador basado ADRC es presentado en la sección 2.4. La sección 3 muestra los resultados de la cosimulación realizada en Matlab-Simulik/PSIM, donde se analiza la efectividad del controlador antes de la construcción experimental, los resultados experimentales se muestran en la sección 4 y, finalmente, en la sección 5 se presentan las conclusiones.
2. Materiales y métodos
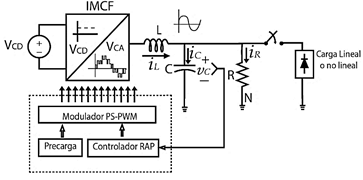
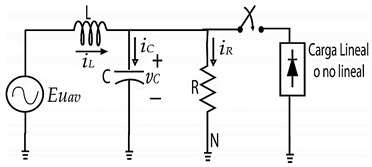
En la Figura 1 se muestra el sistema completo el cual se describe a continuación. A partir de una fuente de voltaje de corriente directa, VCD, el CMCF sintetiza en la salida una señal de múltiples niveles de voltaje basada en PWM. Dicha salida de voltaje es procesada por un filtro pasivo de tipo LC pasa-bajas con el fin de atenuar las componentes de alta frecuencia de la señal PWM y finalmente, obtener una señal de voltaje sinusoidal pura en la salida del filtro. El controlador por rechazo activo de perturbaciones retroalimenta la señal de voltaje del filtro y la compara contra una señal de referencia, de tipo sinusoidal con frecuencia de 60 Hz y amplitud variable; la señal de referencia o moduladora se emplea para el modulador PS-PWM. Durante el encendido del CMCF, los capacitores flotantes están descargados, por lo tanto, por medio del proceso de precarga, se establece el voltaje correcto, o voltaje nominal, en cada uno de ellos. Inicialmente se conecta una carga del tipo resistivo con valor conocido en paralelo al capacitor C del filtro de salida y en determinado momento, se añade una carga de tipo lineal o no lineal como perturbación exógena al sistema. El CMCF se muestra en la Figura 2, este se compone de múltiples celdas de potencia conectadas una después de otra. Cada celda de potencia (excepto la que está conectada al bus de CD), contiene un par de interruptores de potencia y un capacitor flotante.
Por ejemplo, la celda 1 se compone de los terruptores S1, Ŝ1 y del capacitor C1. Para formar siete niveles de voltaje, incluyendo el nivel correspondiente a 0V, se requieren seis celdas. Cada capacitor flotante de la celda i-ésima, debe ser cargado y se debe mantener a un nivel nominal de voltaje VCi el cual puede corresponder con alguno de los siguientes valores: VCD/6, 2VCD/6, 3VCD/6, 4VCD/6, 5VCD/6. Individualmente, cada interruptor del convertidor puede estar cerrado (ON) o abierto (OFF). Con el fin de evitar cortocircuitos en las celdas, los interruptores de cada celda deben operar en forma complementaria, por lo que nunca deben permanecer cerrados al mismo tiempo; esta condición se garantiza empleando un tiempo muerto entre conmutaciones. En la topología de capacitores flotantes, así como en otras topologías multinivel, un mismo nivel de voltaje puede ser formado con distintos estados de conmutación, los cuales se denominan estados redundantes. En la topología de CMCF de medio puente de siete niveles, se pueden obtener en la salida los siguientes niveles de voltaje: −3VCD/6, −2VCD/6, −VCD/6, 0, VCD/6, 2VCD/6, 3VCD/6.
2.1. Modelo dinámico en forma promedio
Aplicando leyes de corriente de Kirchhoff al CMCF mostrado en la Figura 2 se obtiene el conjunto de ecuaciones para las corrientes en los capacitores flotantes:
donde iL es la corriente en el inductor del filtro de salida, Ci es la capacitancia de los capacitores del CMCF, di representa el ciclo de trabajo del interruptor Si y VCi son los voltajes en los capacitores flotantes, con i = {1, 2, 3, 4, 5}. El voltaje de salida del CMCF de la Figura 2, se mide desde el nodo va respecto a tierra y se nombra como vaN, el cual se determina de la siguiente manera:
La modulación PS-PWM genera las señales PWM para cada par de interruptores de las celdas del CMCF. En la Figura 3(a) se muestran algunos ciclos de las señales portadoras C1 a C6, las cuales son señales triangulares con amplitudes que toman los valores de [−1, 1] y frecuencia fc, desfasadas entre sí 60 grados. La frecuencia de las portadoras es mayor que la frecuencia de la moduladora fm, por lo que es común definir un índice de modulación 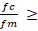 im. En este trabajo se empleó para modulación un índice de modulación im = 40. Para el caso de la señal moduladora uav, toma valores de amplitud de [−1, 1] y posee una frecuencia fm = 60 Hz. Cada señal portadora es comparada con la moduladora; para obtener las señales PWM tal como se puede observar en la Figura 3(b) originando las señales PWM nombradas como Va − Vf, las cuales tienen el mismo ciclo de trabajo d. Al aplicar esta señal al CMCF de siete niveles, todos los interruptores tienen el mismo ciclo de trabajo, es decir:
im. En este trabajo se empleó para modulación un índice de modulación im = 40. Para el caso de la señal moduladora uav, toma valores de amplitud de [−1, 1] y posee una frecuencia fm = 60 Hz. Cada señal portadora es comparada con la moduladora; para obtener las señales PWM tal como se puede observar en la Figura 3(b) originando las señales PWM nombradas como Va − Vf, las cuales tienen el mismo ciclo de trabajo d. Al aplicar esta señal al CMCF de siete niveles, todos los interruptores tienen el mismo ciclo de trabajo, es decir:
Acorde con la Ecuación (1), la variación del voltaje promedio en cada capacitor flotante es nula cuando todos los ciclos de trabajo, d1ad6, son iguales. Por lo tanto, las dinámicas de voltaje en los capacitores flotantes de (1) se pueden considerar constantes y sus derivadas iguales a cero. Esta es la razón por la que la dinámica de los capacitores puede no considerarse en el modelo promedio del CMCF. Por otra parte, existe una relación entre ciclo de trabajo d y la señal moduladora uav, la cual se expresa como d Tomando en cuenta esto y sustituyendo (3) en (2), el voltaje de salida VaN puede expresarse como sigue:
Donde E es el voltaje de cada uno de los capacitores Cb1 y Cb2, mismo que tiene por valor a VCD/2. La ecuación (4) permite ver de manera simplificada al CMCF de siete niveles como un convertidor «reductor» multinivel con una fuente de voltaje de alimentación Euav (donde E = VCD/2), un filtro LC pasabajas y una carga de naturaleza variante, tal como se muestra en la Figura 4.
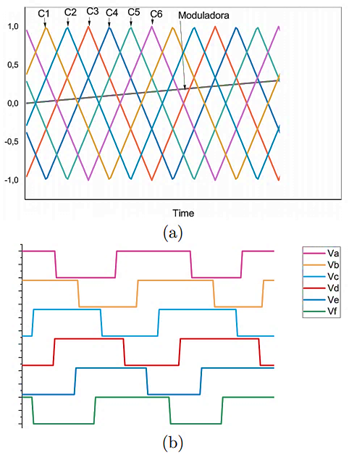
Figura 3. Modulación PS-PWM: (a) Portadoras de la modulación; (b) Ciclo de trabajo en los canales PWM generados
Tomando en consideración lo anterior, el modelo promedio de segundo orden del CMCF se puede expresar como en (5):
La entrada de control uav, representa la señal moduladora PWM que puede tomar valores del conjunto continuo [−1, 1]. El término vC es el voltaje en el capacitor del filtro. La corriente que circula por los interruptores y por la inductancia de salida es iL. L y C son los valores de inductancia y capacitancia del filtro, respectivamente.
2.2. Linealización en forma exacta del modelo
El sistema CMCF así conformado es lineal, de una entrada y una salida (SISO, por sus siglas en inglés, Single Input-Single Output) y como ya se mencionó es de naturaleza reductora. Reagrupando el modelo mostrado en la Ecuación (5) para ser expresado en su forma no lineal afín, se tiene lo siguiente:
Como se describe ampliamente en [17], la función de salida que permite linealizar en forma exacta al sistema no lineal (6) está dada como:
El grado relativo r del sistema no lineal (6) se obtiene mediante el cálculo sucesivo de las derivadas de Lie:
hasta encontrar la derivada de Lie que cumple con:
donde k ∀x∈Ω. Las derivadas de Lie calculadas son:
Dado que (11) es diferente de 0, el grado relativo r del sistema (6) es igual a 2. Se realiza la transformación de coordenadas x a z mediante:
Para verificar si Φ es un difeomorfismo, se verifica la no-singularidad de la matriz jacobiana, dada por:
De (13) se puede demostrar que JΦ es no singular para cualquier x por lo que la transformación de coordenadas es válida. El sistema de coordenadas z se expresa como:
El sistema original (6) se transforma en el sistema linealizado en la forma normal de Brunovsky tal como se muestra a continuación:
La variable v es una la ley de control auxiliar cuya expresión se planteará más adelante y definirá la dinámica de seguimiento que se desea cumpla el sistema. La ley de control se obtiene despejando u de (15), como sigue:
El modelo mostrado en (5) del CMCF considera una carga resistiva R de valor conocido, pero dado que el inversor está sujeto a cargas de naturaleza variante, la corriente de carga iL cambiará su valor dependiendo de la carga, por lo tanto, se causarán perturbaciones en el voltaje de salida del inversor. Como se puede observar, la ley de control de la Ecuación (18), requiere el valor de α(x), el cual a su vez, requiere la medición de iL. Una propuesta para evitar el uso del sensor de corriente se trata a continuación.
2.3. Diseño del controlador ADRC
Basándose en el enfoque ADRC con observador de estado extendido, se diseña un observador LESO [18], para su formulación se realizan las siguientes suposiciones:
-
1. Solo se mide la salida plana F = vC
2. Los valores nominales de los parámetros L, C, R, E son conocidos.
3. La entrada de control uav está disponible.
4. La función de perturbación α(x) es desconocida, pero se considera acotada.
5. Las variables estimadas de la salida plana y su derivada se denotan como F1 = F y F2 = F˙.
6. Las variables estimadas de la función de perturbación y su derivada, son η1 = α(x) y η2 = α(x).
El observador LESO se diseña a partir de (15) y se define como sigue:
El conjunto de coeficientes λ0, λ1, λ2, λ3 son valores constantes y son seleccionados mediante un polinomio Hurtwitz de cuarto orden:
Partiendo de (18) y de (19) se diseña el control ADRC, donde los valores estimados del observador LESO son adaptados al controlador auxiliar de seguimiento:
Donde las señales de seguimiento son:
Con ωn = 2πf y f = 60 Hz.
La ley de control basada en la técnica ADRC se establece como sigue:
En (22), η1 representa el valor estimado de α(x), es decir, η1 = α˙(x). Los coeficientes k0, k1 son valores constantes, seleccionados mediante un polinomio Hurwitz de segundo orden como se muestra a continuación:
3. Simulación del sistema
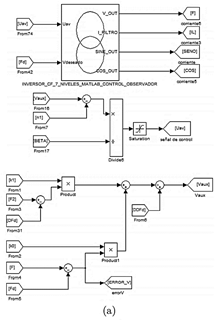
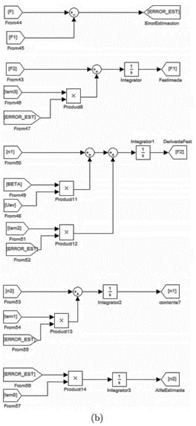
La simulación del sistema se llevó a cabo usando el modulo SimCoupler y fue realizada por medio de una cosimulación entre PSIM 9.0 y MATLAB/Simulink. El controlador se construye en MATLAB/Simulink, esto se muestra en la Figura 5. Por otra parte, en PSIM se realiza la construcción del circuito de precarga y los elementos del inversor multinivel (filtro de salida, modulador PS-PWM y el control para cambios de carga), esto se muestra en la Figura 6. Por tanto, el procesamiento del controlador se realiza en MATLAB/Simulink y se acopla por medio del módulo SimCoupler a PSIM; el valor de la señal de control acoplada tiene por nombre uav y la recibe el modulador PS-PWM como ciclo de trabajo para realizar la acción de control sobre la salida del CMCF.
Para todos los componentes pasivos empleados se consideraron valores nominales de placa con una tolerancia de 20 % para capacitores y de 10 % para resistores e inductores; por lo tanto, para el convertidor multinivel se emplearon los siguientes valores: CCAP 1...CAP 5 = 10 µF; los capacitores del bus de CD tienen un valor de CP C = 1000 µF. Los valores de los elementos del filtro de salida son CF = 4.7 µF, LF = 7 mH y RL = 100 Ω. La señal de referencia de voltaje es igual a V d = A sin(2πf), las pruebas se realizaron para una amplitud deseada de A = 80 V y una frecuencia f = 60 Hz. Por otra parte, la modulación PS-PWM utiliza portadoras con frecuencia de 2.4 kHz. El valor de los parámetros para el observador LESO λ0, λ1, λ2, λ3 se calculan con wn = 30000 y ζ = 0.707. Los parámetros del controlador k0 y k1 se calculan con wnc = 3000 y ζc = 0.707. En ambos casos los polos se ubican en el lado izquierdo del plano complejo a fin de garantizar la estabilidad.
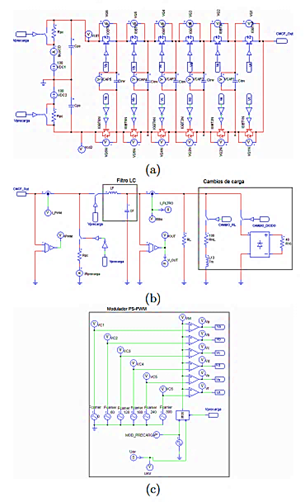
Figura 6. PSIM: (a) Inversor multinivel. (b) Filtro LC a la salida y control de cambio de carga y. (c) Modulador PS-PWM y activación de cambios de carga.
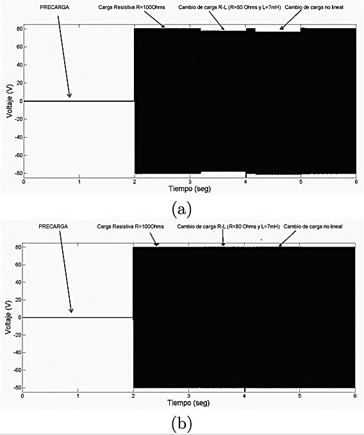
Para comprobar la robustez del controlador ADRC ante cambios repentinos de carga se realizaron dos tipos de pruebas: para una primera prueba, se añade a la salida del inversor, después del filtro, una carga adicional del tipo R − L, con valores nominales de RNL1 = 80 Ω y LNL = 7 mH. El resultado de la simulación se muestra en la Figura 7(a); en esta se puede observar que al realizar el cambio de carga, la corriente iL incrementa su valor y el estimador LESO en conjunto con el controlador ADRC actualizan la señal de control uav, permitiendo que el voltaje del capacitor retome la trayectoria de referencia nuevamente.
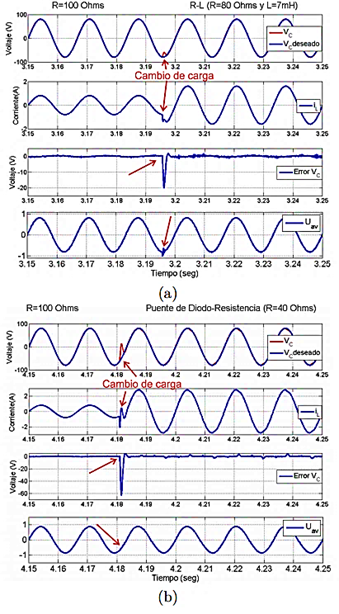
Figura 7. Resultados de simulación: (a) Con carga adicional del tipo R − L. (b) Con carga adicional compuesta por un puente de diodos y una resistencia.
La segunda prueba consistió en agregar ahora una carga no lineal que consiste en un puente de diodos junto a una carga resistiva de 40 Ω. La Figura 7(b) muestra el resultado de la simulación donde se puede observar que al agregar la carga no lineal produce que el voltaje en el capacitor sufra una fuerte desviación transitoria de la referencia sinusoidal deseada, misma que es corregida de la misma manera por la acción del estimador LESO y el controlador ADRC. En la Figura 8 se observa el resultado de la simulación ya con el controlador, del comportamiento del voltaje en los capacitores flotantes durante los cambios de carga realizados en las pruebas anteriores. La precarga de los capacitores flotantes se realiza de acuerdo con el trabajo presentado en [7], ahí proponen un intervalo de tiempo de t = [0 − 2]s. Al realizar los cambios de carga, se observa que los voltajes en los capacitores flotantes se mantienen en forma promedio en sus valores nominales; el rizo se incrementa, siendo mayor cuando se le conecta la carga no lineal del diodo + resistencia. Para validar el efecto del controlador sobre el voltaje de salida vC se realizaron dos pruebas en simulación, la primer, prueba es sin controlador, solo con el modulador PS-PWM; el resultado de esta prueba se puede observar en la Figura 9(a).En la segunda prueba se coloca el controlador propuesto, el resultado se puede apreciar en la Figura 9(b). En esta prueba el voltaje del capacitor vC se mantiene sin cambios o muy poco perceptible cercano a la referencia. En este punto y analizando las figuras mencionadas, se puede argumentar que la modulación PS-PWM por sí misma, no sería capaz de mantener el voltaje de salida.
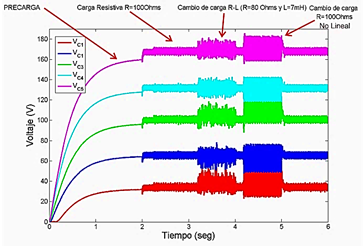
Figura 8. Resultado de simulación de los voltajes en los capacitores flotantes durante la precarga, operación normal y cambios de carga.
4. Resultados experimentales
Para verificar los resultados de simulación se realizó la implementación del sistema que consistió en dos partes principales: la primera, contempla la construcción del prototipo del convertidor multinivel y los sistemas auxiliares para su funcionamiento, la descripción del mismo se muestra en la Figura 10. La segunda parte, es la implementación en un FPGA de los algoritmos del controlador ADRC y el modulador PS-PWM. En [19] se recomienda seguir la metodología top-down que es muy adecuada para implementar algoritmos en los dispositivos de lógica reconfigurable y que ha sido usada con excelente desempeño en [14], [20], [21], [22]. Para llevar a cabo la implementación se empleó el software de Xilinx ISE 14.7, se codificó en VHDL sin hacer uso de alguna herramienta de alto nivel basada en bloques o generación de código, y se ocuparon los elementos internos del FPGA, tales como memorias BRAM y multiplicadores embebidos para optimizar el uso de recursos internos del dispositivo; el diseño realizado se muestra en la Figura 11. Cabe mencionar que para las operaciones aritméticas necesarias se utilizó la representación numérica en punto flotante simple de 32-bits alineado al estándar IEEE-754 y se logró un tiempo de muestreo de 10 µs. Para evaluar el desempeño del controlador se realizaron al igual que en simulación, dos tipos de pruebas: en lazo abierto y en lazo cerrado. En ambos casos se hicieron cambios de carga del tipo lineal y no lineal para verificar el desempeño del controlador propuesto. De manera inicial se probó el prototipo para verificar su funcionamiento correcto, el resultado de esta prueba se muestra en la Figura 12. En la Figura12(a) se puede observar la salida con siete niveles que se toma antes del filtro de salida; las Figura 12 (b) y (c) muestran la salida sinusoidal después del filtro LC para voltaje y la corriente suministrada, respectivamente.
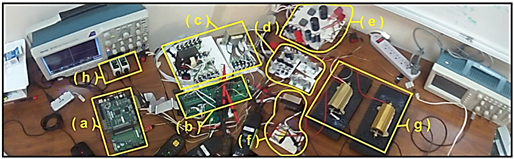
Figura 10. Prototipo desarrollado del inversor multinivel de siete niveles de capacitores flotantes. (a) Tarjeta de desarrollo basada en FPGA (Nexys-2). (b) Inversor multinivel. (c) Fuentes aisladas para impulsores de compuerta e instrumentación. (d) Control de precarga de capacitores y cambio de carga a la salida. (e) Fuente principal de CD. (f)Filtro LC a la salida del inversor. (g) Cargas a la salida del inversor (200 W). (h) Puntas aisladas de medición.
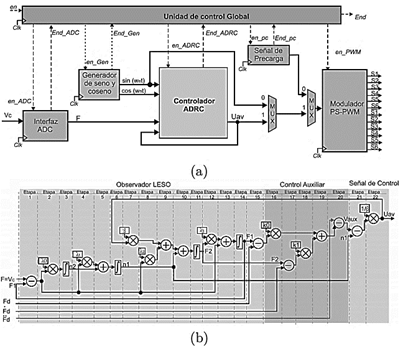
Figura 11. Implementación en el dispositivo FPGA. (a) Diagrama a bloques propuesto. (b) Arquitectura diseñada para la ejecución del algoritmo de control y LESO.
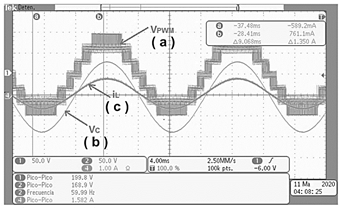
Figura 12. Formas de onda de salida obtenidas del prototipo experimental. (a) Salida de voltaje multinivel de 7 niveles antes del filtro LC (VPWM). (b) Salida de voltaje después del filtro LC (VC). (c) Corriente suministrada a la carga (iL).
Para validar el contenido armónico de la onda de salida del inversor se realizó una prueba con un medidor de calidad de energía (Hioki 3197), el resultado se muestra en la Figura 13, se observa una alta calidad en la onda de salida, tanto en voltaje (T HDv) como en corriente (T HDi).
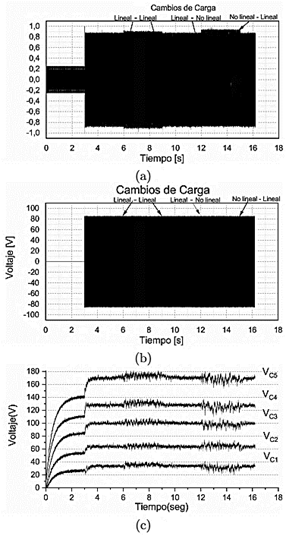
Como resultado de la prueba en lazo abierto la Figura 14 muestra los resultados de tres aspectos que consideramos importantes: la señal de control (uav), el voltaje de salida del convertidor (vC) y el voltaje de los capacitores (VC1...C5). Como ya se ha comentado anteriormente, se realizaron cambios de carga del tipo lineal y no lineal. En la Figura14(a) se muestra el valor de la señal de control con una amplitud fija después de la precarga con un valor de uav = 0.85, el equivalente a un valor deseado de voltaje de salida VC = 85V, el cual se puede observar en la Figura14(b) cuando el sistema es sometido a cambios de carga repentinos. En esta figura podemos observar claramente que durante los transitorios, la amplitud del voltaje se ve afectado, ya que disminuye. En la Figura 14(c) se observa que el balance de los capacitores se mantiene nominalmente dentro de su zona de trabajo, sin embargo, al momento de realizar los cambios de carga se puede apreciar un incremento en el rizo de cada uno de ellos.
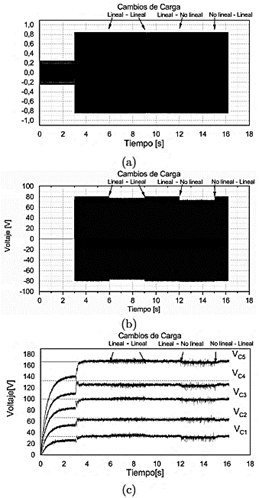
Figura 14. Gráficos de los resultados experimentales obtenidos en lazo abierto ante diferentes cambios de carga. (a) Señal de control (uav). (b) Voltaje de salida del inversor despues del filtro (VC ). (c) Voltaje en los capacitores flotantes VC1...C5.
La prueba en lazo cerrado se realizó bajo el mismo procedimiento que el llevado a cabo para la prueba en lazo abierto. La Figura 15(a) muestra el resultado de la señal de control; después del periodo de precarga, se establece un valor inicial de uav = 0.85 para un valor deseado de VC = 85 ëV, en la misma figura se puede observar la acción del controlador (uav variable) durante la conexión repentina de las cargas. La Figura 15(b) muestra que el voltaje de salida no modifica su amplitud cuando se realizan los cambios de carga. En la Figura 15(c) se muestra el voltaje de los capacitores los cuales mantienen el balance y solo se aprecia un incremento de alta frecuencia en cada uno de ellos.
5. Conclusiones
En términos generales se observa que la disminución en la complejidad del modelo del CMCF ayudó considerablemente en otros aspectos tales como la reducción de la capacidad de cómputo necesaria para procesar el controlador, reducción en el tiempo de procesamiento y a emplear menos sensores en el prototipo. Por otra parte, se puede comentar que es necesario que la modulación PS-PWM mantenga el balance de voltaje de los capacitores flotantes para que el control ADRC funcione, es decir, realice el seguimiento de la referencia de voltaje, sin embargo, la modulación PS-PWM no es capaz de mantener el voltaje deseado a la salida en su valor nominal cuando se presentaron perturbaciones en la corriente de carga. Al agregar el controlador ADRC, la tarea de control se lleva a cabo de manera efectiva. El controlador ADRC y el observador LESO tratan con efectividad la perturbación de corriente, por lo que podemos considerar al controlador robusto ante perturbaciones exógenas provocadas por cambios de carga de tipo lineal y no lineal. La señal de voltaje en el capacitor del filtro sigue efectivamente a la referencia impuesta, salvo desviaciones transitorias, que rápidamente son minimizadas por el controlador. Hay que considerar que, en el caso de desbalance de los capacitores, el control ADRC no es capaz de seguir la referencia de voltaje. El uso del dispositivo de lógica programable para la implementación del sistema, como bien se observa en las pruebas experimentales, contribuyó a tener muy buenos resultados, sobre todo, en términos de rapidez de ejecución del algoritmo y atención a las perturbaciones. Se verificó que los inversores multinivel poseen entre sus características principales una alta calidad en la onda de salida (T HDv < 5 %, como lo marca el estándar IEEE-519) y que la topología de capacitores flotantes, al requerir solo una fuente de CD, es una opción recomendable entre las otras estructuras multinivel ya existentes.