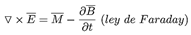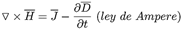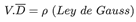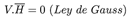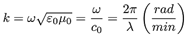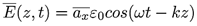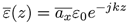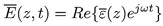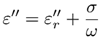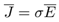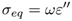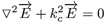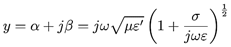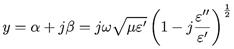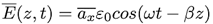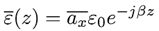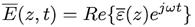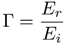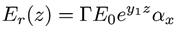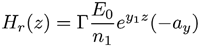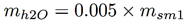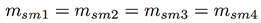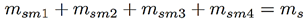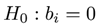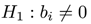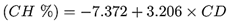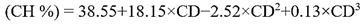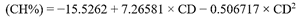Forma sugerida de citación: Abanto, F.; Rotta, P.; LaMadrid, L.; Soto, J.; La Rosa, G.; Manrique, J.; Ruiz, G. y Ipanaque, W. (2020). «Humedad y su relación con la espectroscopía dieléctrica en agregados de concreto». Ingenius. N.◦ 24, (julio-diciembre). pp. 17-27. doi: https://doi.org/10.17163/ings.n24.2020.02.
1. Introducción
El contenido de humedad (CH) de un material es un parámetro que muchos sectores industriales buscan controlar en sus procesos, pues repercute en las características finales del producto. En la industria de la construcción el CH del concreto resulta importante porque define las propiedades mecánicas y la vida útil de un proyecto civil [1]. Se han realizado estudios para analizar la durabilidad y resistencia en estructuras de concreto midiendo el CH [2] y también en probetas de concreto [3] no se han realizado investigaciones de sistemas que midan el CH de ADC en línea con el proceso de mezclado en planta. Autores en [4], [5], [6] muestran diferentes técnicas para lograr la medición del CH de materiales. En el presente artículo se utiliza una metodología basada en espectroscopía dieléctrica (ED) que ha sido probada en suelo [7], lana [8], papel [9], tela [10], harina [11], madera [12], [13], [14]. Existen varios métodos de medición de CH de materiales que se clasifican en directos e indirectos. En los métodos directos se obtiene el CH sin correlacionar con otras variables. Estos son los métodos termogavimétrico y químico.
El método termogavimétrico no es selectivo [15, 16], el rango eficaz de medición varía de 0.5% a 99.9% para el CH, y su exactitud es de 0.5% de la masa total. En contraste, el método químico [17], [18], [19] es selectivo, tiene una precisión de 0.0001 % y un rango de medición de 0.00001 a 99.9% de CH. Los métodos indirectos requieren una calibración previa para obtener el CH usando métodos directos. Los indirectos se clasifican en pasivos y activos. Los primeros utilizan elementos como resistencias o capacitancias variables para determinar la CH, y por su naturaleza es un control invasivo. Los activos son aquellos que emiten ondas electromagnéticas para determinar las características del medio, garantizando de esta manera un control en línea, y la integridad de la muestra al no ser invasivo ni destructivo. Los resultados de las diversas investigaciones en [20], [21], [22], [23] dentro del campo de los métodos activos, demuestra una relación existente entre el CH y la permitividad relativa (ε´) o constante dieléctrica (CD) [24] de un material. Los métodos indirectos usan técnicas como la ED que busca medir la CD del material y también se utiliza para otros fines como caracterizar materiales. Otra técnica indirecta es el uso de imágenes hiperespectrales que ha tenido buen éxito en bioingeniería [25] y en agroindustria [26], [27], [28], [29].
Autores muestran aplicaciones con ED orientadas a la agricultura con el fin de estimar la calidad de sus productos [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], así tenemos aplicaciones en semillas, trigo, granos, nueces, frutos de palma aceitera, plátanos. Este artículo describe conceptos teóricos de la ED y su relación con el CH [6]. Se presenta una aplicación de la ED para buscar la correlación entre el CH y la CD en ADC con diferentes canteras y verificar la posibilidad de este nuevo método en esta industria.
1.1. Descripción de las ondas electromagnéticas
Se denomina campos electromagnéticos al conjunto de campos de fuerzas eléctricas y magnéticas producidas por cargas y corrientes eléctricas en movimiento a través del vacío o algún tipo de materia. Cuando un campo electromagnético se propaga en el espacio se denomina propagación de ondas electromagnéticas. La propagación de ondas electromagnéticas encuentra su fundamento en la solución de las ecuaciones de Maxwell.
Donde:
-
E es el campo eléctrico [V/m]
H es el campo magnético [A/m]
M es la densidad de corriente magnética [V/m2]
f es la densidad de corriente eléctrica [A/m2]
B es la densidad de flujo magnético [Wb/m2]
D es la densidad de flujo eléctrico [Coul/m2]
ρ es la densidad de carga [Coul/m3]
Para resolver las ecuaciones de Maxwell se supone propagación en el espacio libre y, además, un campo senoidal y armónico dependiente del tiempo, que se propague en el eje z y polarizado en el eje x. Al utilizar estas suposiciones y combinar las ecuaciones dadas se genera una ecuación de segundo orden que se conoce como ecuación vectorial homogénea de Helmholtz para E.
Donde k es el número de onda que para un medio sin pérdida y se expresa como:
Donde:
-
ω es la frecuencia angular de propagación
ε0 es la permitividad del vacío
µ0 es la permeabilidad del vacío
Resolviendo:
que toma el valor fasorial:
Para expresar de forma senoidal, el vector fasorial se puede utilizar la siguiente expresión:
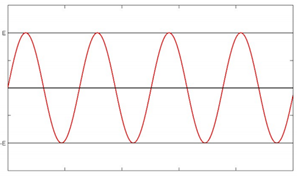
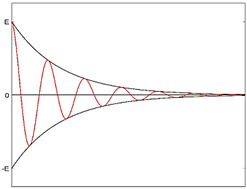
En la Figura 1 se puede observar la propagación del campo eléctrico en el espacio libre, en donde se han tomado las hipótesis dadas.
1.2. Propagación de las ondas en un medio con pérdidas
Las hipótesis definidas en el apartado anterior consideran la propagación de ondas electromagnéticas en el vacío. Se amplían a materiales con pérdidas, es decir, materiales convencionales. Los materiales se clasifican según su comportamiento frente a campos como buenos conductores cuando permiten el paso de campos eléctricos por ellos o como dieléctricos cuando almacenan energía eléctrica en su interior y forman enlaces moleculares polares que se conocen como dipolos eléctricos. Normalmente, un material tiene una parte conductora y otra dieléctrica. Su comportamiento se determina mediante la permitividad compleja del material, que se define como:
Donde ε´ es la constante dieléctrica del material y mide la cantidad de momentos dipolares formados y representa la energía contenida en el material y ε´´ es la constante de pérdidas que representa la energía que no es almacenada en el material, sino que de alguna manera se propaga o refleja y se representa como:
Donde σ es la conductividad del material tal que:
Se obtiene una conductividad equivalente que representa todas las pérdidas en el medio.
La «tangente de pérdidas» es una medida de la pérdida de potencia en el medio y se define.
Por lo tanto, la solución de las ecuaciones de Maxwell a través de la ecuación vectorial homogénea de Helmholtz para E queda de la forma:
Donde kc es el número de onda complejo, es decir, que toma el valor complejo de la permitividad del medio que se comporta de modo fasorial al tomar un campo eléctrico senoidal. Además, la permitividad del vacío queda expresada como un valor real, ya que no tendrá pérdidas:
Por lo tanto, esta forma de comportamiento de los materiales hace que las ondas electromagnéticas se atenúen al momento de incidir en ellas, parte de la energía será almacenada en los enlaces polares y parte se irá en pérdidas de energía. Esto hace que se defina el concepto de constante de propagación como:
Usando la definición de pérdida tangencial.
Donde α es la constante de atenuación y β es la constante de fase. Entonces la solución primaria que se da en el vacío queda como:
que toma el valor fasorial:
Donde:
En la Figura 2 se muestra la representación de esta atenuación de un campo eléctrico que incide en un material con pérdidas.
La energía perdida al momento de la propagación sobre el material, recibe ese nombre porque no se almacena en el material formando enlaces polares, parte de esta energía se refleja del material y parte de ella atraviesa el material, de acuerdo con el valor de conductividad de este. Esto se aprecia en la Figura 3. Se observa un campo eléctrico incidente de verde que al chocar en el medio (de rayas azules) se refleja parte del campo (de rojo) y parte se propaga por el campo (de naranja). Todo esto queda cuantificado en la permitividad compleja. En todo este análisis se asume que el material es isotrópico, es decir, que los momentos dipolares o que los enlaces polares se dan en la dirección del campo eléctrico, en materiales anisotrópicos esto no ocurre, pero este análisis no se toma en cuenta para esta investigación ya que hemos considerado a los ADC isotrópicos.
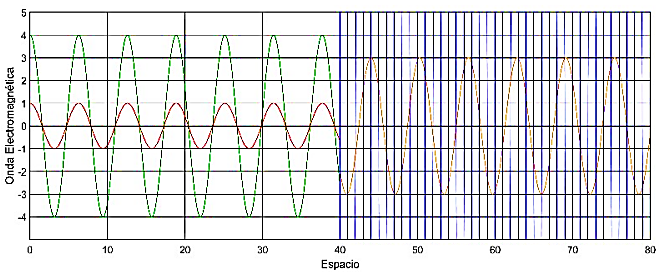
Figura 3. Comportamiento de la propagación de una onda electromagnética frente a un cambio de medio [11].
La parte del campo reflejado se puede relacionar respecto al campo incidente mediante el coeficiente de reflexión Γ que relaciona la onda reflejada y la onda incidente del campo.
Reemplazando la ecuación de la onda para expresarlo en términos de campo eléctrico, sería:
La ecuación del campo magnético de la onda propagada y reflejada se dirige en la dirección ortogonal al campo eléctrico:
Es posible medir el campo eléctrico incidente en un material, el campo propagado y el campo reflejado de acuerdo con las ecuaciones dadas en la teoría. Con todo esto podemos asumir que es posible deducir los valores de CD que tomará el material al analizar la relaciones entre estas cantidades.
1.3. Propiedades dieléctricas de la molécula de agua
El agua es un dieléctrico, es decir, como hemos visto contiene en su estructura moléculas polares que forman momentos dipolares al estar en contacto con un campo eléctrico y por ende a mayor cantidad de agua, mayor será la CD medida. Un material seco tendrá un comportamiento establecido según su estructura molecular y será malmente homogéneo cuando esta estructura se mantenga inalterable al sufrir aumento de temperatura o mezclarse con agua. Los ADC, por su forma y propiedades, presentan una estructura homogénea. Por ende, su constante dieléctrica permanecerá inalterable cuando se humedezca. Sin embargo, a mayor humedad se incrementará el momento dipolar de la mezcla por el agua presente, lo que ocasionará que la CD de la mezcla cambie debido al aumento de agua. Por lo tanto, la CD de la mezcla se verá relacionada con el CH de los ADC y si podemos medir el CH y la CD de la mezcla podemos determinar una correlación entre estas para una futura predicción y utilizarla como sistema de sensado.
2. Metodología
Se ha visto en el apartado anterior que es posible correlacionar el valor del CH de los ADC con la CD de la mezcla ya que la cantidad de momentos dipolares aumentará de acuerdo con su CH. Además, se ha visto teóricamente que es posible determinar la CD de la mezcla utilizando las ecuaciones de Maxwell y su solución para medios con pérdidas. En este apartado se brinda la metodología experimental que se ha seguido para realizar dicha correlación. Es preciso recalcar que el campo emitido es el campo que choca con el material, y el campo propagado es el que atraviesa el material.
2.1. Materiales
La ED usa frecuencias en el rango de las microondas para la propagación de los campos electromagnéticos, por lo tanto, se utilizan dos antenas de apertura para emitir y recibir los campos incidente y propagado respectivamente. Ver Figura 4.
También se ha utilizado un sistema de análisis de señales vectoriales para emitir el campo electromagnético como se ve en la Figura 5. Se analiza la variación de la fase y amplitud de la señal para posteriormente determinar la CD.
El analizador de señales vectoriales utiliza un software para detección de datos. También se ha construido una plataforma de sensado para realizar la experimentación, sobre la que se ha colocado el ADC para medir su CD y su CH. Otros materiales utilizados han sido: balanzas, recipientes de medición, horno de secado, etc. La muestra se deposita entre la antena receptora y la transmisora, donde se mide el efecto de la onda sobre los ADC al propagarse en el espacio libre entre las dos antenas.
2.2. Experimentación
Se han utilizado tres canteras peruanas de ADC para realizar la calibración del sistema: Cerro Mocho, Moyobamba y Sol-Sol. Para obtener la correlación CH vs. CD se ha proseguido de la siguiente manera: Se ha definido una masa inicial (m0) como la masa total de ADC proporcionado por la cantera. Luego se ha realizado un secado termogavimétrico en horno para obtener el valor de masa seca (ms), esto quiere decir, sin CH. Este valor de ms se ha dividido en 4, cada una de estas muestras se ha denominado masa seca de muestreo y se han numerado del 1 al 4 (msmx), el x en el subíndice corresponde a la numeración de la submuestra. Se procede a seleccionar la msm1 y se coloca sobre la plataforma de sensado, se emite el campo electromagnético sobre el material y con ayuda del analizador de señales se mide el valor de la CD de la msm1. Este valor de CD corresponde al valor de 0 % de CH. A este valor de msm1.se le agrega masa de agua (mH2O) correspondiente a 0.5 %msm1 y se procede a realizar el mismo procedimiento de medición de su CD. Luego se vuelve a añadir 0.5 %msm1 y se mide su CD que corresponde al 1 % de su CH. Este procedimiento se repite hasta que se llega al 10 % de CH.
Se debe aclarar que se cumplen las siguientes relaciones en la experimentación:
La distancia entre antenas fue de 23 cm, el espesor de la muestra se estableció en 40 mm y la frecuencia de emisión del campo electromagnético fue de 1.5 GHz. Se utilizaron msm1 y msm2 para realizar las curvas de correlación y msm3 y msm4 para validar los resultados. Cabe resaltar que en todo momento se mide la CD de la mezcla de ADC húmedo.
3. Resultados
Con los valores de CD vs. CH obtenidos para cada cantera se ajusta la curva de calibración mediante modelos de regresión lineal. En este ajuste el CH se establece como variable dependiente y la CD como variable independiente con diferentes efectos: lineal, cuadrática, cúbica y de cuarto grado. Para la selección del modelo de regresión lineal se aplicó el método Stepwise Forward para encontrar cuál de los efectos de la CD se ajusta mejor con el CH. Este método clásico para la selección de variables inicia con un modelo vacío y en cada iteración evalúa incorporar algunos de los efectos definidos: lineal, cuadrático, cúbico y de cuarto grado de la constante dieléctrica. Se decide incorporar algunos de los efectos mencionados si cumple el nivel de significancia definido: Valor P menor a 0,05. El método Stepwise Forward finaliza cuando no se puede incorporar más efectos por no cumplir el nivel de significancia. Para evaluar el nivel de significancia de los efectos se realiza una prueba de hipótesis con T-Student. En esta prueba se verifica si el coeficiente estimado del efecto es igual o diferente de cero.
Si se rechaza la hipótesis nula (bi = 0 6 ) el efecto es significativo. En el contraste de hipótesis se calcula la relación entre el coeficiente estimado del efecto (bi) y su desviación estándar (Sbi ), y se compara con el t crítico para un nivel de confiabilidad de 95 % (α = 0, 05).
Cochrane-Orcutt para corregir la autocorrelación presente en los datos. Esta autocorrelación es producto de agregar secuencialmente la variación de humedad y con esta corrección se mejora la estimación de los parámetros. Los resultados de las pruebas se presentan a continuación.
3.1. Cantera Cerro Mocho
El modelo se seleccionó mediante Stepwise Forward, donde se obtiene:
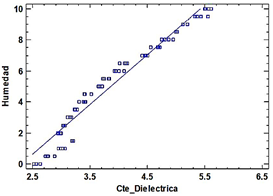
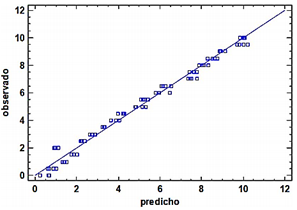
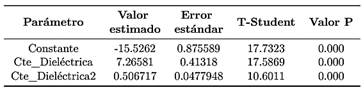
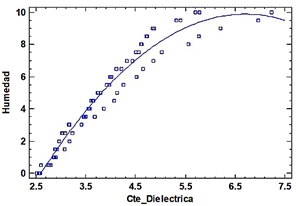
En este modelo el efecto lineal del coeficiente dieléctrico con respecto al valor de humedad esperado resulta significativo. En la tabla siguiente se muestran los resultados del contraste de hipótesis donde el «valor P» del efecto lineal es menor a 0.05. Se tiene un modelo de regresión lineal de R2 = 95.8057 % y un error estándar de 0.382134.
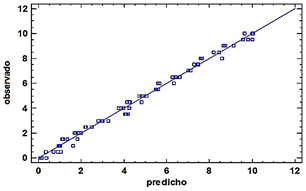
La Figura 6 muestra la relación entre la constante dieléctrica y la humedad; la Figura 7, la relación del valor predicho y el real de la humedad.
3.2. Cantera Moyobamba
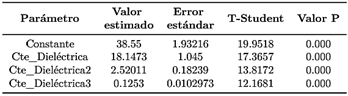
El modelo se seleccionó mediante Stepwise Forward. Donde el efecto lineal, cuadrático y cúbico del coeficiente dieléctrico con respecto al valor de humedad esperado son significativos.
En la Tabla 2 se muestran los resultados del contraste de hipótesis donde el «valor P» de los efectos es menor a 0.05.
Se tiene un modelo de regresión lineal de R2 = 99.5097 % y un error estándar de 0.201714.
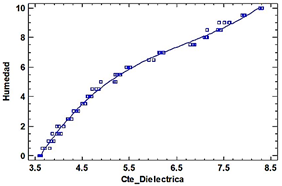
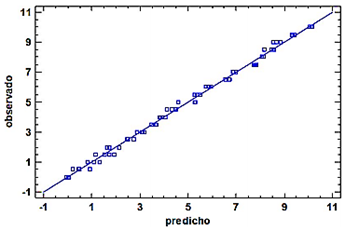
La Figura 8 muestra la relación entre la constante dieléctrica y la humedad; la Figura 9 indica la relación del valor predicho y el real de la humedad.
3.3. Cantera Sol-Sol
El modelo se seleccionó mediante Stepwise Forward.
Donde el efecto lineal y cuadrático del coeficiente dieléctrico con respecto al valor de humedad resultaron significativos. En la Tabla 3 observamos que el «valor P» de los efectos es menor a 0.05.
Se tiene un modelo de regresión lineal de R2 = 97.1325% y un error estándar de 0.297068. La Figura 10 muestra la relación entre la constante dieléctrica y la humedad, mientras que en la Figura 11 se observa la relación del valor predicho y el real de la humedad.
4. Discusión de resultados
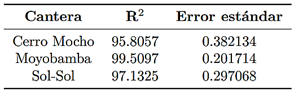
Dados los resultados en el apartado anterior, es interesante ver que en la frecuencia de 1.5 GHz, las correlaciones de regresión lineal mantienen un R2>95 % como se ve en la Tabla 4.
También se puede ver que existe una relación directa entre el CH y la CD, es decir, a mayor CH la CD aumenta en valor. Comparando las ecuaciones de predicción del CH podemos observar que dependiendo de la procedencia del ADC se define su curva de calibración y esta puede variar entre lineal, cuadrática o cúbica, por lo que para fines prácticos primero se debería calibrar el ADC según una cantera específica antes de realizar la medición y esta curva no serviría para otra cantera, ya que los valores de CD difieren entre canteras. Esto era de esperarse ya que la CD depende de las propiedades moleculares y de la capacidad de almacenamiento de energía, lo que significa que a nivel molecular cada ADC tiene diferente estructura.
5. Conclusiones
La medición del CH con dispositivos que utilizan microondas tiene ventajas sobre los métodos invasivos porque no dañan el material. La medición de la CD con esta metodología analiza internamente el comportamiento del material para definir su CD, ya que estudia los momentos dipolares formados al inducir campos electromagnéticos en el material. Puede ser usado en presencia de vapores o ambientes sucios, mientras no cambien molecularmente al ADC ya que estos no interfieren con las señales de microondas. La ED, por lo tanto, permite la medición de una amplia gama de materiales, ya sean sólidos, gases o líquidos. La medición se realiza sin contacto con el material. El método es no invasivo ni destructivo. La medición se realiza en tiempo real y en línea con el proceso. Es interesante observar la relación encontrada por diferentes autores. En [17] el autor define una relación lineal o polinómica. Muestra los parámetros que influyen en el cálculo de la constante dieléctrica y la relación entre el contenido de humedad y la temperatura. Se ha comprobado que con la metodología basada en ED a 1.5 GHz se obtienen valores de correlación lineal de alta precisión (R2>95 %) para cada una de las canteras. El sistema ha sido validado en un transportador horizontal con agregado fino y antenas dispuestas de forma vertical. Los resultados encontrados muestran la relación entre el CH y la CD en ADC, se ha podido apreciar que existe una variación en la curva de calibración entre una cantera y otra. Este sistema de sensado presenta un alto potencial para ser usado para medir el CH en ADC en el proceso de fabricación de concreto.