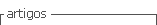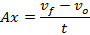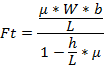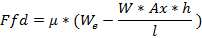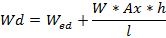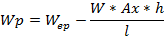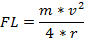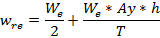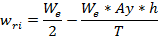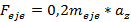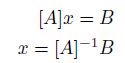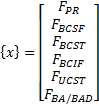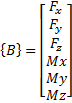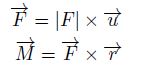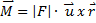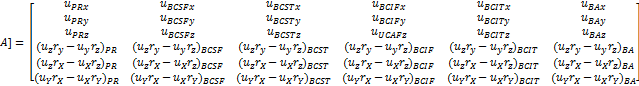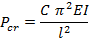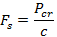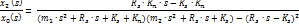Introducción
Fórmula Student es una competencia estudiantil organizada por la SAE (Society of Automotive Engineers o Sociedad de Ingenieros Automotrices) cuyo objetivo principal es fomentar la mejor formación de jóvenes ingenieros [1], desafiando a los estudiantes universitarios a diseñar, construir y probar el rendimiento de un vehículo tipo formula que cumpla exitosamente con las pruebas estipuladas en el reglamento respectivo [2], para luego competir con otros estudiantes de todo el mundo. Los avances tecnológicos y el nivel de competitividad que genera la Formula Student, han motivado al equipo UPS Racing Team de la Universidad Politécnica Salesiana desarrollar dos monoplazas, el primero fue un monoplaza a combustión para la competencia del 2014 en UK, mientras que el segundo fue un vehículo eléctrico para la competencia de Formula Student Electric de UK en 2017.
De acuerdo con los resultados del año pasado [3], en los eventos dinámicos el monoplaza eléctrico ha tenido inconvenientes con algunos sistemas mecánicos y eléctricos; entre los sistemas mecánicos está la falta de ajustes en los reglajes y la amortiguación de la suspensión, así como un fallo localizado en un miembro del brazo de control inferior de la suspensión posterior. Considerando que la suspensión desempeña un papel muy importante en el rendimiento de los vehículos en términos de seguridad y confort, se presenta la necesidad de realizar estudios de la suspensión que permitan establecer mejoras ya sea en la puesta a punto o en el diseño con el fin de que el monoplaza pueda ser competitivo.
El principal diseño de suspensión en competición es el paralelogramo deformable (doublé A-arm o double wishbone), que puede disponer de tres formas de accionamiento del conjunto muelle-amortiguador como es el directo, por medio de varilla de empuje (push-rod) o varilla de tracción (pull-rod) [4]. Estos sistemas de suspensión son de diseño sencillo, de fácil ajuste, resistentes, de buena adaptabilidad y pueden llegar a ser ligeros si son hechos con materiales compuestos, razón por la cual son muy utilizados por los monoplazas de Formula 1 y de Formula Student [5].
La suspensión debe incorporar un buen diseño cinemático para mantener el neumático lo más perpendicular posible al pavimento, una amortiguación óptima y tasas de elasticidad adecuadas para mantener el neumático en el suelo en todo momento. Además, los componentes tienen que ser resistentes para que no fallen bajo las cargas estáticas y dinámicas [6], [7], [8], [9].
El objetivo de este trabajo es realizar el estudio dinámico y cinemático del sistema de suspensión del vehículo eléctrico Formula Student, mediante programas de simulación cinemática y de cálculos matemáticos para determinar el rendimiento de la suspensión y establecer mejoras o soluciones a los problemas que se presentan durante el estudio.
Métodos y materiales
Vehículo de estudio
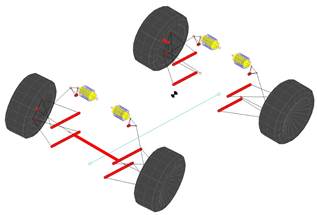
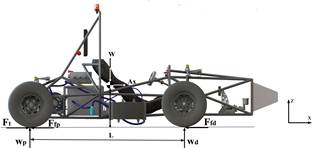
El vehículo que se utiliza para realizar el estudio de la suspensión es un monoplaza de competencia eléctrico Formula Student, como se muestra en la Figura 1.
Las dimensiones del monoplaza se muestran en la Tabla 1.
Características del sistema de suspensión
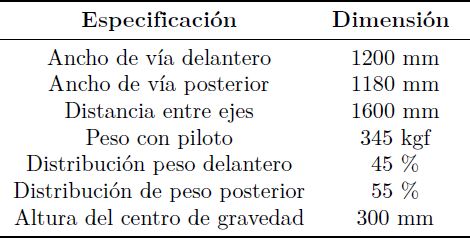
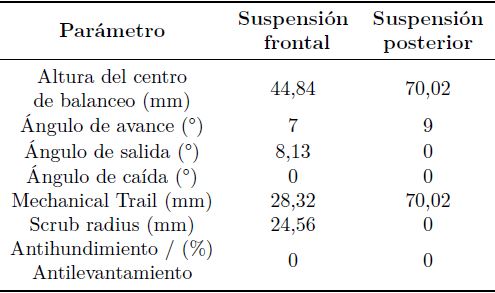
Las características del sistema de suspensión se muestran en la Tabla 2.
Parámetros geométricos
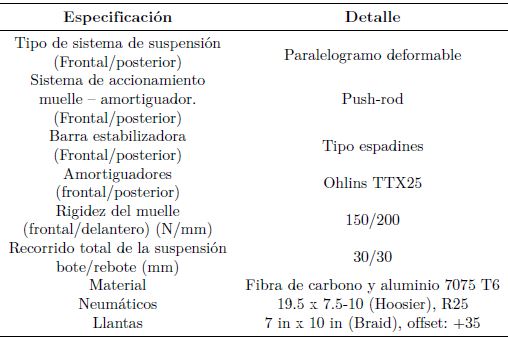
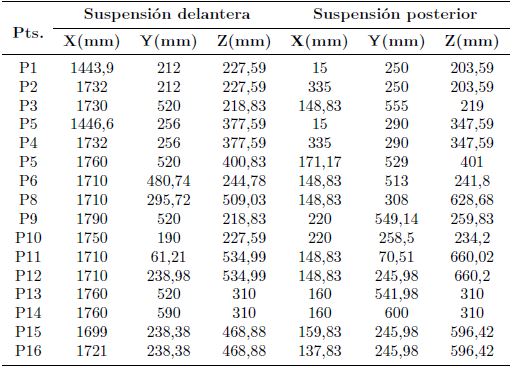
Se determinan las coordenadas de los puntos de conexión de cada elemento de la suspensión, como se muestra en la Tabla 3. Los puntos de conexión además de permitir definir los parámetros geométricos de la suspensión son necesarios para el programa de simulación de la cinemática y para el cálculo 3D de las fuerzas en los miembros de la suspensión.
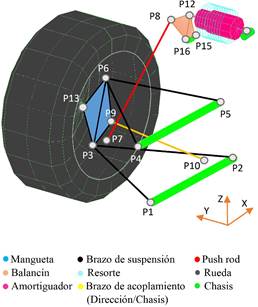
En la Figura 2 se muestra la ubicación de los puntosde conexión de los elementos de la suspensión.
En la Tabla 4 se muestran los parámetros geométricos determinados basados en las dimensiones de la rueda, ancho de vía, la distancia entre ejes y las coordenadas de los puntos de conexión de la suspensión según [6], [7].
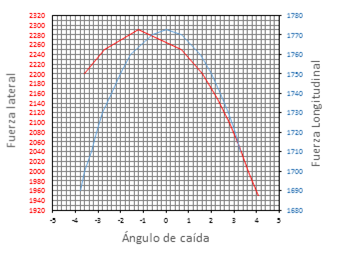
Se realiza un análisis de los resultados del FSAE TIRE TEST CONSORTIUM [10], referentes al neumático Hoosier® 19,5 x 7,5-10, que dispone el monoplaza de estudio. El análisis se efectúa con fin de determinar el rango de ángulos de caída aceptables, el comportamiento del neumático y una predicción de las fuerzas máximas que puede soportar. En la Figura 3 se muestra que la máxima fuerza lateral se presenta para un ángulo de caída de –1° a –1,3°, mientras que la máxima fuerza longitudinal se realiza para una caída de 0°. El neumático no sufre una caída brusca en la adherencia tras alcanzar el pico máximo, por lo que se puede establecer un rango de caída efectivo de 1 a –3°.
Resultados y análisis cinemático
Utilizando Lotus Suspension Analisys se realiza un análisis cinemático del sistema de suspensión. El programa permite conocer el comportamiento de la suspensión con la geometría establecida frente a varios estados en pista como bote y rebote, balanceo y giro de la dirección [11]. Los parámetros que se analizan son aquellos que caracterizan el comportamiento de la suspensión [12], como:
Para la simulación se insertan en el programa las dimensiones del monoplaza y las coordenadas de los puntos de conexión de cada elemento de la suspensión. Lotus crea un modelo tridimensional del tipo de suspensión a analizar como se muestra en la Figura 4.
Se analiza la elevación o el rebote de la suspensión en dirección vertical, lo que trata de simular es el paso del monoplaza por un bache u obstáculo de 30 mm de altura. Para este análisis se considera solo la rueda derecha del eje frontal y posterior, debido a que las ruedas izquierdas presentan un comportamiento similar.
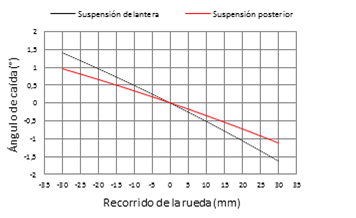
La Figura 5 muestra que las ruedas delanteras en la situación de bote tienen una ganancia de caída negativa máxima de –1,13°, y en rebote una caída positiva máxima de 0,9°. Las ruedas posteriores en la situación de bote tienen una ganancia de caída negativa máxima de –1,63°, y en rebote una caída positiva máxima de 1,41°. El comportamiento del ángulo de caída es favorable según [13], debido a que cuando el vehículo pase por una curva, la rueda más cargada tendrá una ganancia de caída negativa y la rueda descargada una ganancia de caída positiva, mejorando el agarre lateral y a su vez la tracción. Con el fin de conseguir el máximo de las prestaciones del neumático y reducir el ángulo de caída positivo se puede establecer un ángulo de caída estático para la rueda delantera y posterior de –1° y –1,5° respectivamente. Las ruedas al disponer de una caída estática, con la máxima compresión se acercan a una caída negativa de –2,6°, manteniéndose dentro de un rango efectivo de 1° y –3°, según el análisis de los neumáticos. De acuerdo con la recomendación de Carroll Smith [9], se puede reducir el ajuste de caída estática mejorando el agarre del neumático tanto en curvas como en trayectorias rectas.
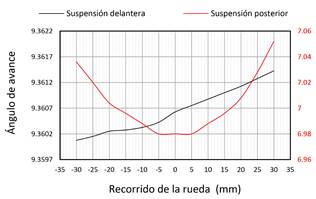
De acuerdo con la Figura 6, el ángulo de avance delantero se hace positivo con el bote de la rueda y negativo con el rebote, mientas que el ángulo de avance posterior tiene una orientación positiva tanto en bote como rebote. El ángulo de avance contribuye a la ganancia del ángulo de caída durante un giro. Según los resultados, el ángulo de avance provocará durante las curvas que la rueda externa tenga una ganancia de caída negativa y la caída de la rueda interna tienda a ser positivo.
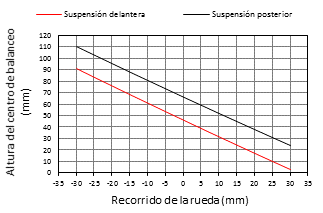
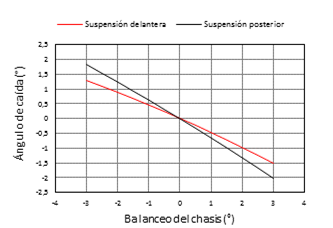
En la Figura 7 se muestra que el máximo recorrido vertical del centro de balanceo con el bote y rebote es de 80,344 mm y 86,4 mm para la suspensión delantera y posterior respectivamente. El centro de balanceo se mantiene en todo momento encima del plano del suelo, algo muy deseable según [14]. La altura del centro de balanceo al centro de gravedad y el efecto anti balanceo de los elementos elásticos, permiten que el ángulo de balanceo del chasis sea de 1° a una aceleración lateral de 1 G, sin considerar la deformación de los neumáticos.
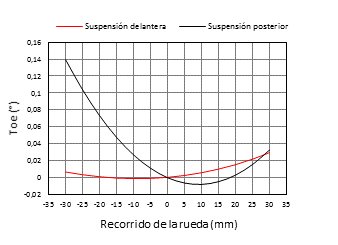
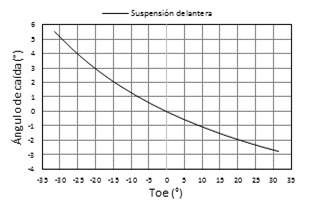
El toe posterior máximo es 0,1393 grados con rebote de la rueda y toe delantero máximo es 0,0328 grados con bote de la rueda, como se muestra en la Figura 8. Un toe ligeramente positivo reduce la resistencia al rodamiento y un toe negativo mejora la maniobrabilidad en curvas, sin embargo, el toe excesivo eleva el desgaste de los neumáticos. Los valores bajos se deben a que el efecto de bump steer es nulo, el cual se ha conseguido con una correcta geometría de los tirantes de dirección.
ç
Se simula el paso del coche en curva, el cual hace que la suspensión se incline por efecto de la aceleración centrífuga, la fuerza lateral se traduce en ángulo de balanceo del chasis. De acuerdo con la Figura 9, cuando el balanceo del chasis es positivo la rueda es externa a la curva y si es negativo la rueda es interna a la curva. Con un balanceo de 3° del chasis, el ángulo de caída máximo para la rueda externa e interna del eje delantero es de 1,28 y –1,52 grados respectivamente, mientas que en el eje posterior el máximo ángulo de caída es de 1,83° para la rueda exterior y –2,01 para la rueda interior. En función de los resultados, las ruedas externas a la curva tienen una ganancia de caída negativa, permitiendo una mejora en la adherencia de los neumáticos.
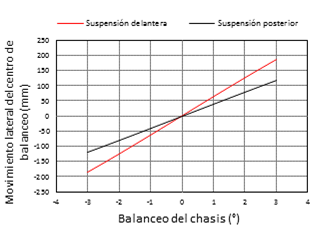
En la Figura 10 se observa que los centros de balanceo posterior y delantero tienen un recorrido lateral de 186,44 mm y 119,05 mm respectivamente, con un balanceo máximo de 3° del chasis. Considerando el efecto en la reducción del balanceo de los elementos elásticos (muelles y barra estabilizadora), así como una aceleración lateral de 1 G; el chasis tendrá 1° de balanceo, donde la migración lateral del centro de balanceo será de 63,57 mm/G y 40,25 mm/G en la suspensión delantera y posterior respectivamente.
La Figura 11 muestra el comportamiento de la rueda delantera derecha con el giro de la dirección. Cuando la rueda es interna a la curva y con el ángulo de giro máximo tiene una caída negativa de –2,75 grados. Si la rueda es externa a la curva, con el giro máximo se genera una caída positiva de 5,33°.
Resultados y análisis dinámico
Se realizan los cálculos de las fuerzas que se generan en los miembros del sistema de suspensión cuando el vehículo está sometido a diferentes escenarios de carga dinámica. Es importante considerar tantos escenarios como sea posible porque las fuerzas generadas variarán para cada miembro en función del caso de carga. Se establecen cinco escenarios de carga diferentes a las que el vehículo se somete en un entorno típico de carretera [15].
Aceleración lineal
Frenado lineal
Paso por curva
Aceleración en curva
Frenado en curva
Paso por obstáculo
Para cada escenario de carga se calculan las fuerzas que se generan en el sistema referencial, X en dirección longitudinal al vehículo, Z en dirección perpendicular al suelo y Y en dirección transversal al vehículo. Las fuerzas que se generan en el parche del neumático en las direcciones X y Z debido a la aceleración y frenado como se muestra en la Figura 12, vienen definidas por las ecuaciones 1-6:
Donde:
Ax = aceleración longitudinal (m/s2)
vo = velocidad inicial (m/s)
vf = velocidad final (m/s)
Ft = fuerza de tracción (N)
W = peso del vehículo (N)
l = distancia entre ejes (m)
h = altura del centro de gravedad (m)
μ = coeficiente de adherencia
Wed = peso estático sobre del eje delantero (N)
Wep = peso estático sobre del eje posterior (N)
Wd = peso dinámico sobre el eje delantero (N)
Wp = peso dinámico sobre el eje posterior (N)
Ffd = fuerza de frenado en el eje delantero (N)
Ffp = fuerza de frenado en el eje posterior (N)
b = distancia del eje posterior al centro degravedad (m)
Las fuerzas que se generan en el parche del neumático en las direcciones Y y Z debido al paso por curva como se muestra en la Figura 13, se determinan por las ecuaciones 7, 8, 9.
Donde:
m = masa del vehículo (kg)
v = velocidad del vehículo (m/s)
r = radio de curvatura (m)
Ay = aceleración lateral (m)
We= peso estático sobre el eje (N)
Wre= peso dinámico sobre la rueda exterior (N)
Wri= peso dinámico sobre la rueda interior (N)
T = ancho de vía (m)
h = altura del centro de gravedad (m)
Las fuerzas que se generan en el parche del neumático en la dirección Z debido al paso por obstáculo se determinan mediante la ecuación 10:
Donde:
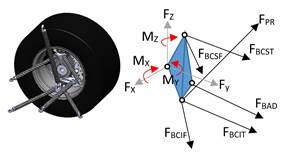
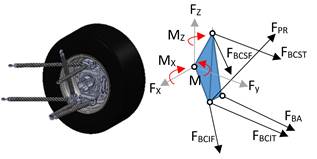
Con los escenarios de carga establecidos, se procede a determinar las fuerzas que se generan en los miembros de la suspensión. En la suspensión frontal y posterior hay un total de seis miembros, en donde dos miembros son del brazo de control superior (BCS), dos miembros del brazo de control inferior (BCI), uno de la barra push-rod (PR) y uno del brazo de acoplamiento (BA). Para este análisis se supone que la carga actúa en el centro de rueda. El centro de rueda se considera como base del cuerpo rígido y el punto (0, 0,0) como se muestra en las Figuras 14 y 15.
Por medio de un sistema de vectores y matrices se determinan cómo se distribuyen estas fuerzas a lo largo de cada uno de los elementos de suspensión [16]. Con un equilibrio de fuerzas y momentos con respecto a los ejes coordenados X, Y y Z del centro de rueda se determinan seis ecuaciones. El sistema de ecuaciones se resuelve por la siguiente expresión:
x representa la fuerza desconocida en cada uno de los miembros de suspensión.
B representa las fuerzas y momentos en X, Y y Z generados en el centro del parche del neumático y resuelto sobre el centro de la rueda.
La matriz A queda determinada por los vectoresunitarios obtenidos de la sumatoria de fuerzas y momentosen las direcciones X, Y y Z de cada miembro.El vector fuerza ( ) es igual al producto punto entreel vector unitario (u) y la magnitud de la fuerza (
) es igual al producto punto entreel vector unitario (u) y la magnitud de la fuerza (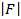 ),como muestra la ecuación 15. El momento (
),como muestra la ecuación 15. El momento (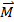 ) es igualal producto cruz entre el vector fuerza () y el vectorde brazo de momento (
) es igualal producto cruz entre el vector fuerza () y el vectorde brazo de momento (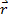 ), como se puede observar enla ecuación 15.
), como se puede observar enla ecuación 15.
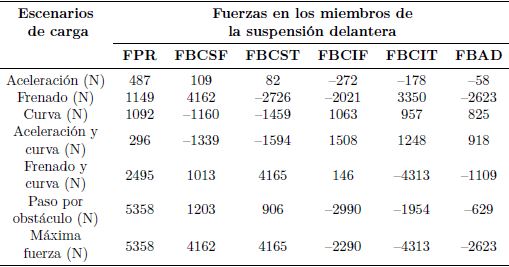
En las Tablas 5 y 6 se muestran las máximas fuerzasde tensión y compresión en los miembros del sistema desuspensión, como resultado de los diferentes escenariosde carga. Las máximas fuerzas de tensión en los miembrosde los brazos de suspensión son de -4313 N y -5131N en la parte delantera y posterior respectivamente,y las máximas fuerzas de compresión son de 4165 Ny 5119 N. Las barras push-rod delantera y posteriortrabajan solo a compresión donde las fuerzas son de5358 N y 8544 N para la parte delantera y posteriorrespectivamente.
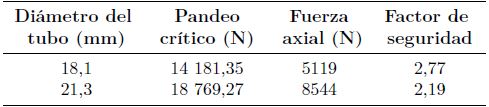
Se realizan ensayos de compresión y tracción para determinar si los miembros soportan las máximas cargas calculadas. En la prueba de tracción se mide la fuerza de unión entre los injertos de aluminio y el tubo de fibra de carbono [17]. El injerto es un elemento de aluminio pegado con un adhesivo de alta resistencia al tubo de fibra de carbono, permitiendo el anclaje al chasis o a la mangueta por medio de rótulas. Los tubos son de dos diámetros externos, de 18,1 mm y 21,3 mm con un espesor de 1,15 mm, El tubo de mayor diámetro es utilizado para la barra push-rod y los brazos de acoplamiento. El tubo de menor diámetro es utilizado para los brazos de suspensión.
Según resultados de la Tabla 6, se puede decir que los miembros de los brazos de suspensión podrían fallar en tensión ya que de acuerdo con el ensayo de tracción la fuerza de unión máxima es de 2,9 KN, y la fuerza de tensión máxima en un miembro del brazo de suspensión es de –5,13 KN. Para el caso de compresión los miembros están sometidos a pandeo, por lo tanto, es necesario realizar un cálculo de pandeo crítico (Pcr) y del factor de seguridad (Fs) definidos por las ecuaciones 18 y 19. El cálculo permitirá predecir con más exactitud un caso de falla por compresión [18].
Donde:
C = constante de condición de extremos articulados
P = fuerza axial (N/m2)
E = módulo de elasticidad del material (N/m2)
I = momento de inercia (m4)
l = longitud de la barra (m)
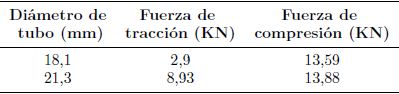
De acuerdo con los resultados de la Tabla 7, los miembros de los brazos de suspensión, push-rod y brazo de acoplamiento no fallarían por efectos de pandeo ya que según el cálculo tienen factores de seguridad mayores que 2 y soportan fuerzas de compresión mayores a 13 KN.
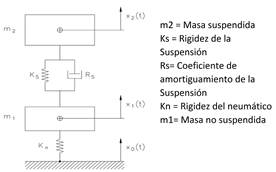
Dado que una de las tareas más importantes delsistema de suspensión es absorber las irregularidadesdel camino sin perder tracción en los neumáticos, lagran mayoría de los autos están equipados con amortiguadoresy resortes que cumplen con ello. En estasección mediante un modelo de 2 grados de libertaddel sistema de suspensión de 1/4 de vehículo [19], serealiza el análisis de las frecuencias de la suspensión,haciendo una interacción entre el camino y el vehículo.En la Figura 16 se muestra el modelo de la suspensiónde un cuarto de vehículo de 2 grados de libertad, endonde incluye la constante elástica del neumático, asícomo la masa no suspendida. La posición de la masasuspendida es X1, de la masa no suspendida es X2 yX0 sirve para modelar las irregularidades del terreno.
La función de transferencia de 2 grados de libertadviene dada por la siguiente expresión:
Con el modelado definido se establecen los parámetrosiniciales necesarios que permitan realizar elestudio como se muestra en la Tabla 9.
La fuerza desarrollada por un amortiguador (Fa ) está representada por la ecuación:
Donde:
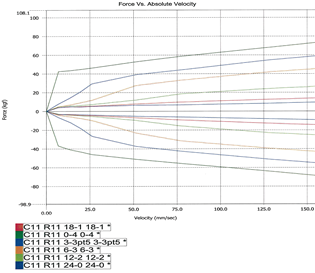
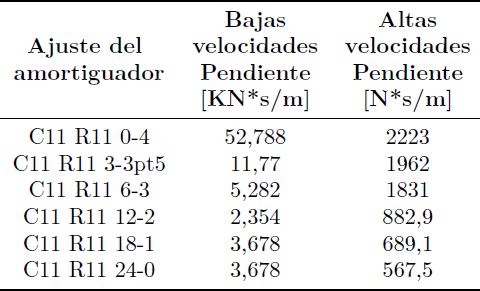
Usando el software matemático Matlab se analizala transmisibilidad del sistema de suspensión a diferentescoeficientes de amortiguamiento para alta y bajavelocidad que provee el amortiguador TTX 25 [20].Por medio de la ecuación 21 y la gráfica de la Figura17 se determinan las pendientes o coeficientes de amortiguaciónpara los diferentes ajustes del amortiguadorcomo se muestra en la Tabla 10.
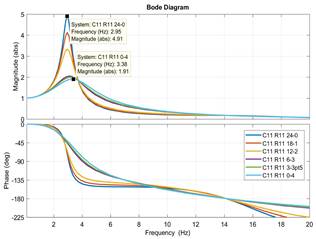
Para maximizar el área de tracción, se requiere la menor transmisibilidad posible. En las gráficas de las Figuras 18 y 19 se muestra la respuesta del modelo de segundo grado de la suspensión frontal y posterior. Se puede observar que si a bajas frecuencias de entrada se aumenta el factor de amortiguación, la transmisibilidad se reduce al máximo, lo que significa que el neumático no perderá tracción. Después del punto de intersección, los factores de amortiguamiento bajos resultan con una menor transmisibilidad, atenuando el movimiento en el chasis [22].
De acuerdo con el análisis de transmisibilidad esnecesario un alto factor de amortiguamiento (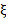 ) a bajasvelocidades y un valor bajo para altas velocidadesen el amortiguador. El amortiguador TTX25, para lasuspensión delantera necesita un valor muy cercanode
) a bajasvelocidades y un valor bajo para altas velocidadesen el amortiguador. El amortiguador TTX25, para lasuspensión delantera necesita un valor muy cercanode 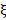 = 0, 73, el cual se logra con el ajuste C11 R11 6-3para baja velocidad. Para altas velocidades el ajusteC11 R11 24.0 provee un
= 0, 73, el cual se logra con el ajuste C11 R11 6-3para baja velocidad. Para altas velocidades el ajusteC11 R11 24.0 provee un  = 0, 22. En la suspensiónposterior se necesita un valor de
= 0, 22. En la suspensiónposterior se necesita un valor de 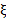 = 0, 68, el cual selogra con el ajuste C11 R11 0-4 para baja velocidad.Para altas velocidades el ajuste C11 R11 18.1 proveeun
= 0, 68, el cual selogra con el ajuste C11 R11 0-4 para baja velocidad.Para altas velocidades el ajuste C11 R11 18.1 proveeun 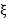 = 0, 22.
= 0, 22.
Como el sistema se mueve tanto a compresión comoextensión, según [23] es mejor tener un factor de amortiguamientomenor a compresión y mayor a extensióncon relación al valor deseado para lograr evitar resonancia en el sistema (ver Figura 20).
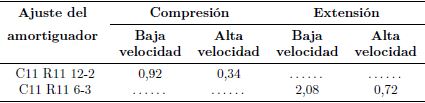
De acuerdo con el análisis realizado se estableceutilizar el doble del factor de amortiguamiento de compresiónpara la extensión. De esta forma, se logra conseguiruna buena adherencia de la rueda, una menortransmisimilidad y mejor maniobrabilidad. Las calibracionesque cumplen con estos requisitos se muestranen las Tablas 11 y 12.
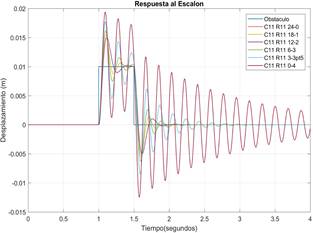
Las Figuras 21 y 22 muestran la respuesta delsistema de la suspensión delantera y posterior respectivamenteante un desplazamiento vertical como entrada.Se puede observar que las calibraciones del factorde amortiguamiento de baja velocidad en compresiónatenúan en el menor tiempo posible las oscilacionescon respecto a otras calibraciones.
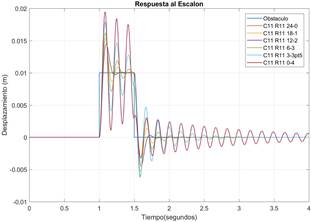
Figura 21. Respuesta del sistema de suspensión delanteraante un desplazamiento vertical como entrada.
Conclusiones
Esta investigación ayuda a tener una visión más amplia de los sistemas de suspensión que utilizan los vehículos de competencia FSAE. Con el estudio de la cinemática se determinó el comportamiento de la suspensión del monoplaza bajo diferentes escenarios en pista, como el paso por curva o por un obstáculo. En función de los resultados se puede decir que la configuración que dispone la suspensión del monoplaza, permite un buen control direccional del vehículo (efecto bump steer nulo) y una ganancia de caída negativa adecuada de la rueda con el recorrido de la suspensión o el balanceo del chasis, dotando de un buen agarre lateral a los neumáticos, sin embargo, con el giro de la dirección hay una ganancia de caída positiva excesiva en las ruedas delanteras, que afectaría el agarre lateral en curvas muy cerradas. Con los ajustes adecuados en los ángulos de avance, salida, caída estática y convergencia, se podría asegurar las condiciones requeridas u óptimas de estabilidad del vehículo y de la dirección, permitiendo mayores aceleraciones, mejor frenado y pasos por curva más rápidos. De acuerdo con el estudio de las fuerzas en los miembros de la suspensión ante cargas dinámicas, se determinó que los brazos de suspensión sometidos a cargas de tensión pueden fallar en los casos críticos, el problema está en la fuerza de unión entre los injertos de aluminio. Con el modelo de segundo grado de un cuarto de vehículo y con la ayuda de Matlab, se realizó un análisis de transmisibilidad que permitió definir las características que el amortiguador debe tener para garantizar máxima área de contacto, lo que produce una mayor tracción.