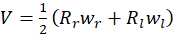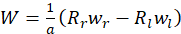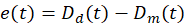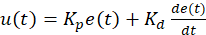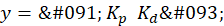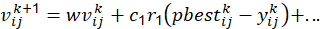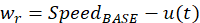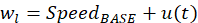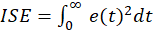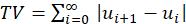1 Introducción
En los últimos años, el control de robots móviles autónomos ha tenido un notable avance en el ámbito de la investigación. En dependencia de la aplicación que se de a dichos robots y como la información de datos es generada a partir de los sensores permitiendo analizar el entorno y la planificación de trayectorias. Por ejemplo en Van Turennout & Honderd (1992), se discute que la distancia y la orientación del robot respecto a una pared puede ser calculada para realizar el seguimiento con el objetivo de identificar lugares desconocidos. Mediante el uso de métodos tradicionales de control, el rendimiento del robot se ve afectado directamente debido a la precisión de los sensores, la señales adquiridas presentan ruidos provenientes de otras fuentes de señales no deseadas al detectar obstáculos. En consecuencia, el detectar dichos obstáculos y posicionar correctamente el robot frente a una pared se vuelve un problema lleno de incertidumbres como se describe en Al-Mutib et al. (2016). Por esta razón varios autores han propuesto diferentes enfoques inteligentes con el objetivo de disminuir este problema. El uso de un algoritmo mejorado de colonia de abejas (IABC) o la utilización de controladores de lógica difusa (FLC) con funciones de membresía permiten mejorar el desempeño de dicho controlador (Chen et al., 2017). Los controladores difusos se han convertido en populares aplicaciones de ingeniería, especialmente para sistemas complejos o que poseen gran incertidumbre en el conocimiento del entorno en el que se desarrollan, como los robots móviles autónomos. Un controlador difuso mejora el rendimiento y la efectividad de un controlador clásico PD para el seguimiento de pared por medio del ajuste de las funciones de membresía (Desouky & Schwartz, 2009). Las pruebas para medir el desempeño del controlador propuesto son a través de simulaciones que no permiten observar como se comporta el sistema por la interferencia del ruido en los sensores. Aljanaideh & Demirly (2010) presentan una nueva metodología difusa utilizada para la sintonización de la ganancia del controlador para pruebas de seguimiento de paredes. Otro enfoque que presenta un controlador de lógica difusa es presentado por Li & Wang (2015), el controlador combina toda la información adquirida por varios sensores láser con el objetivo de seguir paredes desconocidas. Todos estos estudios que se han detallado anteriormente muestran que los controladores de lógica difusa implementados en robots móviles, mejoran considerablemente las acciones de control dirigidas a los motores, generando un movimiento más real al seguir una pared. El siguiente trabajo presenta la implementación de dos controladores para el seguimiento de paredes y analizar la efectividad de cada uno de ellos, el primero es un controlador clásico PD y el otro es un controlador PD con lógica difusa para mejorar el seguimiento, tanto para cambios de referencia de la distancia entre robot-pared y para el seguimiento de una pared desconocida. Estos controladores son sintonizados a través de un algoritmo de optimización conocido como enjambre de partículas (PSO), el cual permite generar un gran desempeño en el sistema. La integral del error cuadrático (ISE) y la variación total de la acción de control (TV) fueron los índices utilizados para medir el desempeño de los controladores. El índice ISE analiza la respuesta del sistema en estado transitorio y el índice TV estudia la calidad de las acciones de control. El robot móvil empleado en esta investigación fue DaNI 2.0, la cual es una plataforma educativa desarrollada por National Instruments y ha sido utilizado por Villacrés et al. (2017) para el seguimiento de referencias. La distancia entre el robot y la pared es medida a través de un sensor ultrasónico montado en la parte frontal del robot.
La organización de este documento es la siguiente: La sección 2 describe la metodología empleada para resolver el problema de seguimiento de pared. La sección 3 presenta el diseño del controlador PD con lógica difusa y la sintonización a través de PSO. La sección 4 ilustra la implementación de los controladores y los resultados experimentales. Finalmente, las conclusiones de esta investigación son reflejadas en la ultima sección.
2 Metodología
Este trabajo utiliza la investigación descriptiva. La investigación descriptiva permite aplicar los conceptos necesarios para encontrar el modelo cinemático del robot móvil, el problema del seguimiento de pared y el procedimiento para desarrollar los controladores para que el robot móvil cumpla este objetivo. Toda esta información es recolectada en artículos científicos, libros y sitios web académicos.
2.1 Descripción de la plataforma de robot móvil
El robot móvil de tracción diferencial utilizado en este trabajo es la plataforma DaNI 2.0, el cual fue desarrollado por las empresas Pitsco Education y National Instruments. Posee dos motores, cada uno con un encoder en cuadratura incorporado para la medición de velocidad y posición del robot; además, contiene un sensor ultrasónico que mide la distancia. La placa de control es un NI Single-Board RIO (FPGA), el cual se programa mediante el software LabView Robotics. El robot DaNI 2.0 se muestra en la figura 1 y las características mecánicas y eléctricas son presentadas en la tabla 1.
Tabla 1: Características del robot DaNI 2.0. Fuente: (Browne & Conrad, 2017)
| Parámetros | Valor |
|---|---|
| Radio de las ruedas | 0.1016[m] |
| Distancia entre las ruedas | 0.3937 [m] |
| Velocidad Angular máx | 2 [rad/s] |
| Velocidad lineal máx | 0.5 [m/s] |
| Cable Ethernet | CAT 5 |
| CPU | NI 9623 sbRIO |
| Sensor Ultrasónico | 0.05-1.2 [m] |
2.2 Problemas del seguimiento de pared y modelo cinemático
El seguimiento de pared se caracteriza por mantener una cierta distancia entre el robot y la pared (Van Turennout & Honderd, 1992). Para cumplir este objetivo se debe proporcionar una orientación y velocidad adecuada al robot para.
La distancia elegida en este trabajo debe ser mayor a D 𝑑 =0.25𝑚 para conservar un rango de seguridad para evitar accidentes o colisiones en las pruebas de seguimiento. Según Cheng et. al (2004), la pared es elegida bajo los siguientes supuestos que se indican a continuación:
• La curvatura de la pared debe ser suficientemente mayor que el radio de giro del robot móvil.
• La señal del error es la diferencia entre la distancia medida por el robot y la distancia deseada determinada por el diseñador.
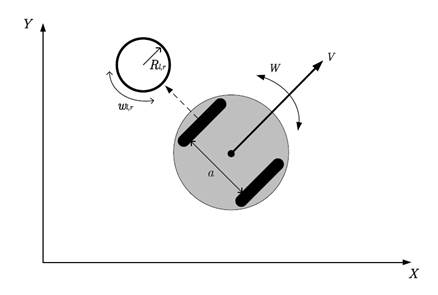
A continuación se modela al robot DaNI 2.0, el cual es un robot de tracción diferencial, donde 𝑉 es la velocidad lineal del robot y 𝑊 es la velocidad angular del robot como se muestra en la figura 2 (Salem, 2013).
Las ecuaciones de la cinemática para este robot son presentadas en (1) y (2).
donde 𝑅 𝑟 , 𝑅 𝑙 son los radios de la rueda derecha e izquierda respectivamente, 𝑤 𝑟 , 𝑤 𝑙 son las velocidades angulares de cada rueda y 𝑎 es la distancia entre las dos ruedas.
3 Diseño del Controlador
3.1 Controlador PD
Para el diseño del controlador PD es necesario definir el error de seguimiento. El error está definido por la siguiente ecuación (3):
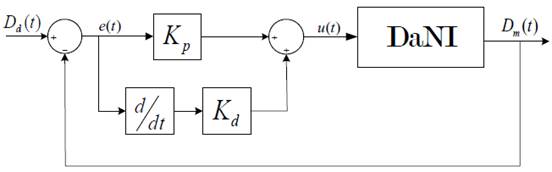
donde 𝐷 𝑑 (𝑡) es la distancia deseada y 𝐷 𝑚 (𝑡) es la distancia medida entre el robot y la pared. El esquema de control del controlador PD es mostrado en la figura 3.
El controlador PD es representado mediante la notación (4).
donde ?? 𝑝 y 𝐾 𝑑 son parámetros de sintonización.
3.2 Controlador PD-Difuso
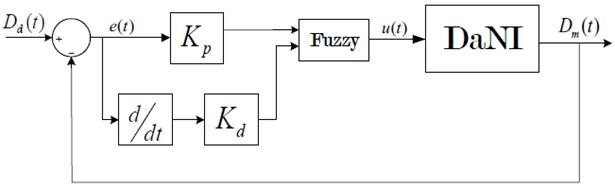
Con el objetivo de mantener la distancia deseada entre el robot-pared y observar como la lógica difusa mejora el desempeño del controlador PD se diseña un controlador difuso. Este controlador posee dos entradas: el error 𝑒(𝑡) y la derivada del error 𝑒 (𝑡); por otro lado, la salida es la acción de control 𝑢(𝑡). El esquema del controlador PD-Difuso es ilustrado en la figura 4. La selección adecuada del controlador PD-Difuso está basada en el conocimiento cualitativo sobre el proceso que va a ser controlado, el mismo que es definido por medio del software Matlab/Simulink y el uso de Fuzzy Logic Toolbox (Desouky & Schwartz, 2009; Villácres et al., 2017).
A continuación se detallan los pasos para realizar un controlador con lógica difusa:
1. Diseño de las funciones de membresía para la fuzzificación de las variables de entrada y salida.
2. Implementación de las reglas de inferencia difusa usando la función IF-THEN.
3. Comprobación del resultado de la variable de salida a través del visor de reglas.
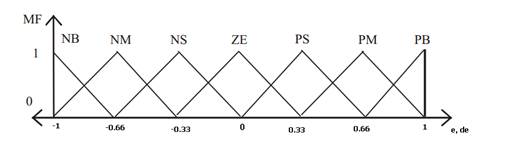
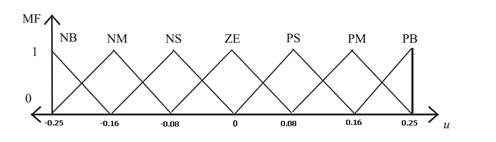
En este trabajo se eligieron siete funciones de membresía (MFs) con el objetivo de suavizar las acciones de control con la siguiente descripción: NB (Negative Big), NM (Negative Medium), NS (Negative Small), ZE (Zero), PS (Positive Small), PM (Positive Medium), and PB (Positive Big). El rango del universo de discurso para las variables de entrada 𝑒(𝑡), 𝑒 (𝑡) es [-1 1]. Este rango es escogido dependiendo del error máximo que se ha establecido en el desarrollo del controlador. Para la variable de salida 𝑢(𝑡) es [-0.25 0.25], cuyo rango es escogido de acuerdo a la velocidad mínima requerida en esta investigación. Cada una de las funciones de membresía son definidas como triángulos simétricos con un 50% de solapamiento entre cada una de ellas (Ghosh et al., 2015). Las funciones de membresía son mostradas en las figuras 5 y figura 6.
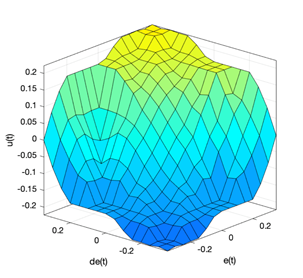
La superficie difusa de salida es mostrada en la figura 7. Fahmizal & Kuo (2013) presentan cuarenta y nueve reglas de control difuso, sobre las cuales se basa el presente estudio y son presentadas en la tabla 2.
3.3 Sintonización a través PSO
Particle Swarm Optimization es una técnica aplicada para resolver problemas de optimización de alta complejidad (Xue et al., 2019). Este método se basa en el comportamiento colaborativo de sistemas biológicos que están agrupados por enjambres en la naturaleza. En este caso es utilizado para encontrar valores óptimos de sintonización para el controlador clásico PD, buscando minimizar la función de costo. El índice de desempeño escogido como función de costo es: la integral del error cuadrático (ISE). En este estudio, es necesario escoger un vector candidato, donde se encuentran los parámetros que se requieren optimizar (Biswas et al., 2014). El vector de solución candidato es(5) , (6) y (7)
Donde 𝐾 𝑝 es la componente proporcional y 𝐾 𝑑 es la componente derivativa del controlador PD. El procedimiento para llevar a cabo dicho algoritmo consiste en iterar las siguientes ecuaciones: (6)
Donde 𝑖 es el número de partícula, 𝑗 es el número del parámetro de sintonización, 𝑘 es el número de iteración, 𝑦 es el vector candidato que contiene los parámetros de sintonización, 𝑣 es la velocidad de la partícula, 𝑝𝑏𝑒𝑠𝑡 es la mejor solución particular, 𝑔𝑏𝑒𝑠𝑡 es la mejor solución global, 𝑟 1 y 𝑟 2 son números aleatorios entre 0 y 1, 𝑐 1 y 𝑐 2 son constantes positivas de las tasas de aprendizaje y 𝑤 es el factor de restricción (Noureddine et al., 2013). La función de costo 𝑓 es definida como la integral del error cuadrático(8)
donde 𝑒(𝑡)= 𝐷 𝑑 (𝑡)− 𝐷 𝑚 (𝑡) y la función de costo 𝑓 serán usadas para encontrar los parámetros de sintonización a través de la reducción del índice de desempeño ISE.
Los parámetros escogidos para la iteración de este algoritmo fueron: 20 iteraciones, 15 partículas con un rango de [0 5], 𝑐 1 =1.7, 𝑐 2 =1.3 y 𝑤=0.95. Estos parámetros fueron escogidos a través de simulaciones buscando obtener el mejor desempeño del controlador, al final se obtuvo: 𝐾 𝑝 =4.023 y 𝐾 𝑑 =0.12.
3.4 Implementación de los controladores
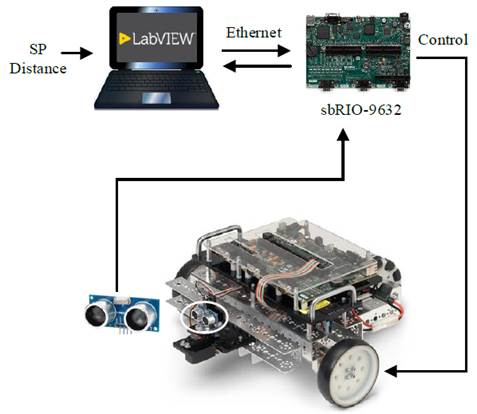
Los controladores fueron implementados en el robot DaNI 2.0 que es compatible con el software LabView Robotics 2017. Los experimentos llevados a cabo fueron realizados mediante un computador Intel(R) Core(TM) i7-5500U CPU @ 2.40GHz con 8.00 GB de RAM. El setpoint (SP) de la distancia deseada entre el robot y la pared es enviada por el computador mediante comunicación TCP/IP al sistema embebido sbRIO-9632 y la lectura de la distancia del robot respecto a la pared es medida por medio del sensor ultrasónico. Por lo tanto, la tarjeta sbRIO-9632 calcula las acciones de control necesarias para controlar al robot DaNI 2.0 para que siga la pared. La figura 8 muestra el esquema de funcionamiento utilizado para las pruebas presentadas.
Con el objetivo de que el robot móvil realice el seguimiento de pared, la técnica utiliza se la conoce como Left Wall-Following presentada en Fahmizal & Kuo (2013), donde la velocidad de las ruedas está dada por las siguientes ecuaciones: (9) y (10)
donde 𝑆𝑝𝑒𝑒 𝑑 𝐵𝐴𝑆𝐸 es la velocidad lineal promedio del robot móvil dado por el fabricante, en este caso es 0.4 e/𝑠 y 𝑢(𝑡) es una velocidad mínima que proviene del controlador (acción de control). Finalmente, los parámetros de sintonización 𝐾 𝑝 =4.023 y 𝐾 𝑑 =0.12 fueron adquiridos a través del algoritmo PSO como se mostró en la sección 3.3. Los índices de desempeño para evaluar los controladores son la integral del error cuadrático y la variación total de la acción de control y son dados por las siguientes ecuaciones (Klan & Gorez, 2008): (11) y (12)
4 Resultados experimentales
En esta sección se describe las dos pruebas realizadas para comparar el desempeño de los controladores detallados anteriormente. La primera prueba pone en evidencia a los controladores para que el robot pueda seguir una pared desconocida. Por otro lado, en la segunda prueba, el robot móvil debe ser capaz de seguir diferentes cambios de la distancia de seguimiento entre el robot y la pared.
4.1 Prueba de seguimiento de una pared desconocida
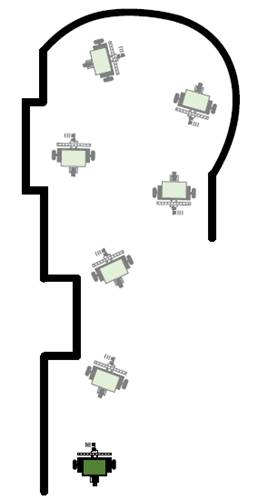
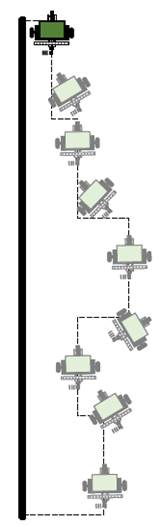
En esta prueba se realiza el seguimiento de una pared desconocida con una distancia de 𝐷 𝑑 =0.45𝑚 entre el robot móvil y la pared. El esquema de la prueba vista desde la parte superior es ilustrada en la figura 9.
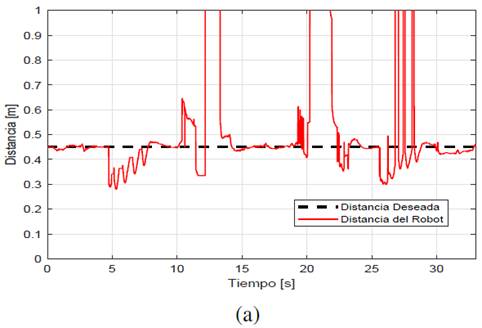
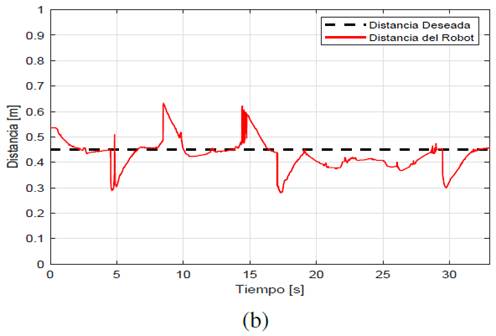
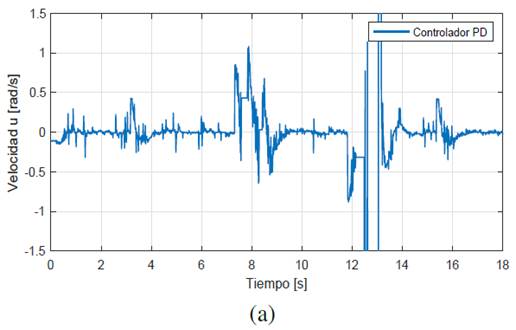
La figura 10a y figura 10b presenta el desempeño de cada controlador y se observa que el controlador PD muestra cambios repentinos en su comportamiento al seguir una pared desconocida tratando de mantener la distancia entre el robot y la pared constante. El experimento puede ser visto en el siguiente enlace: https://youtu.be/gVP7zJcMH78.
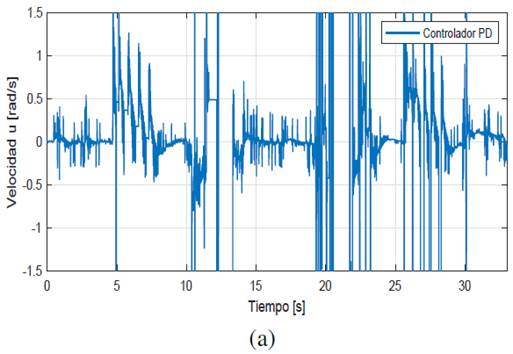
La figura 11a y figura 11b ilustra las acciones de control de ambos controladores en esta prueba donde las acciones del controlador PD-Difuso presentan menor magnitud.
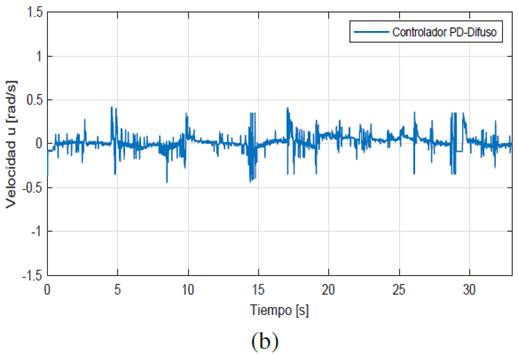
Figura 11: Prueba de seguimiento de una pared desconocida - acciones de control. (a) PD. (b) PD-Difuso.
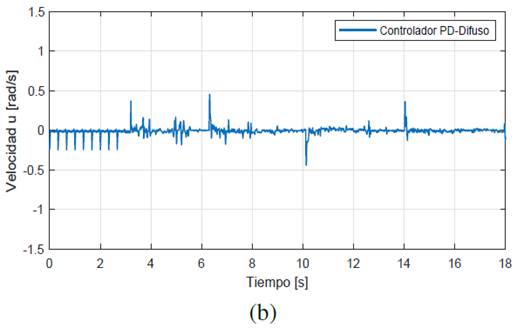
Figura 14: Prueba de cambio de distancia entre el robot y la pared - acciones de control. (a) PD. (b) PD-Difuso.
La tabla 3 muestra los índices ISE y TV para cada uno de los controladores en la prueba de seguimiento de una pared desconocida donde el controlador PD-Difuso presenta menores sobrepicos que el controlador clásico PD, permitiéndole aumentar la vida útil de los motores.
4.2 Prueba de cambio de distancia entre el robot y la pared
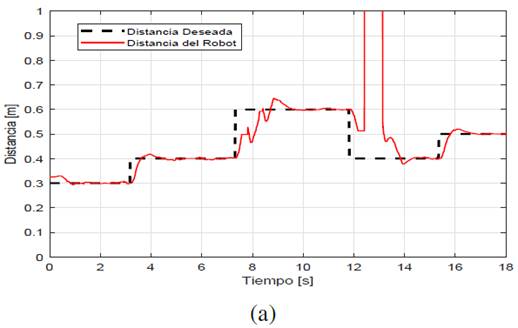
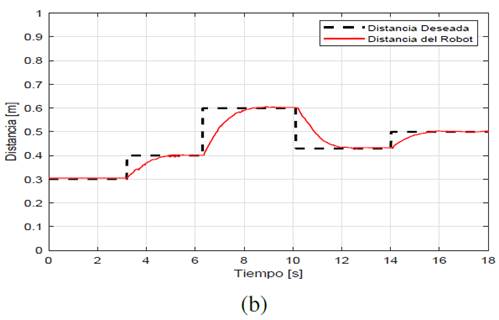
En esta prueba se realizaron cambios de 0.1𝑚 y 0.2𝑚 en la distancia deseada 𝐷 𝑑 . La figura 12 ilustra los diferentes cambios que se ejecutaron en la prueba para verificar si ambos controladores logran cumplir este objetivo. El controlador PD no puede alcanzar cambios de 0.2𝑚 porque el robot móvil pierde el seguimiento al tratar de llegar a esa nueva referencia mientras que el controlador PD-Difuso no tiene problemas en seguir los cambios de referencia realizados. Este comportamiento puede ser visto en la figura 13a y figura 13b.
La figura 14a y figura 14b describe las acciones de control de ambos controladores para esta prueba donde el controlador PD-Difuso presenta acciones de control suavizadas que el controlador convencional PD.
La tabla 4 presenta los índices ISE y TV para cada uno de los controladores en la prueba de cambio de distancia entre el robot y la pared donde el desempeño del controlador PD-Difuso muestra valores más bajos en los índices ISE y TV cuando los cambios son realizados.
5 Conclusiones
En este trabajo fueron implementados dos controladores con el objetivo de realizar un seguimiento de pared. El primero se trató de un controlador PD sintonizado a través de PSO y a partir de éste, se implementó el controlador PD basado en lógica difusa, los cuales fueron comparados a través los índices ISE y TV. El controlador PD-Difuso presentó valores más bajos en ambos índices, tanto, para al seguir una pared desconocida como al seguir diferentes cambios de referencia. Al usar un controlador PD-Difuso, el robot móvil presentó una respuesta más acertada al seguir la pared y mantener una acción de control uniforme.