Introducción
El conocimiento financiero es esencial para una entidad comercial determinada. La salud financiera expresa la buena situación financiera de la empresa. Una empresa es financieramente sana si garantiza los fondos invertidos (rendimiento, rentabilidad), es financieramente estable, no está limitada en su toma de decisiones por otras entidades (endeudamiento, estructura financiera), puede pagar sus obligaciones y, por lo tanto, garantizar la existencia y la apreciación de los fondos invertidos (Gavurova et al., 2020; Krulicky y Horak, 2021).
Por otra parte, la crisis financiera puede definirse como una situación en la que el flujo de caja de una empresa se restringe por alguna razón. Esta restricción puede ser temporal si los directores tienen la oportunidad y la capacidad de llevar a cabo procedimientos correctivos (Liew et al., 2023). Horak et al. (2020) mencionan características similares de dificultades financieras, y la definen como un estado en el que la salud financiera de la empresa se debilita significativamente. Los autores añaden que, en caso de existir dificultades financieras, es difícil para la empresa establecer un calendario de pagos y pagar sus obligaciones financieras a tiempo dentro de las fechas de vencimiento pre-acordadas, lo que expone a la empresa al posible riesgo de intervención legal. En tal situación, la empresa muestra graves problemas de liquidez (capacidad de pago), y la solución equivale a cambios significativos en las actividades operativas de la empresa y el método de financiación (Vochozka et al., 2020). La crisis financiera es también la etapa final del deterioro organizacional antes de la bancarrota. Por lo tanto, la dificultad financiera difiere de la quiebra ya que prescribe un momento en el que el prestatario no puede pagar las deudas al acreedor (Hantono, 2019). Todavía no se ha determinado la definición exacta de dificultades financieras, sin embargo, se sabe que las dificultades económicas poseen diversos grados. La dificultad financiera leve se refiere a la dificultad temporal en el flujo de caja y conceptos como insolvencia, impago, etc. El más peligroso de estos grados es la bancarrota o el fracaso empresarial (Shi y Li, 2019).
La importancia de predecir las dificultades financieras ha evolucionado gradualmente desde hace casi medio siglo cuando se observó este fenómeno contemporáneo que apareció con el desarrollo de los establecimientos comerciales, donde el repentino quiebre de muchas empresas resultaba incomprensible. Kliestik et al. (2018) afirman que existen varios trabajos científicos que han estudiado el tema de la predicción de las dificultades financieras, con el fin de predecir el quiebre de la empresa y clasificar la empresa de acuerdo con su salud financiera. Para ello, se han utilizado varios métodos que difieren en sus supuestos y complejidad. Sin embargo, anticiparse a las dificultades financieras antes de que ocurran sigue siendo una de las soluciones que han demostrado ser eficaces para evitarlas. Inicialmente, se utilizaron técnicas estadísticas para construir modelos con capacidad predictiva, y la construcción de modelos se asoció con el desarrollo de la ciencia y la tecnología. Cuanto más se desarrolla la ciencia, hay más científicos e investigadores que diseñan modelos más complejos, precisos y de calidad que llenan los vacíos de los estudios anteriores. El desarrollo de la ciencia ha llevado a una revolución en el campo del pronóstico, donde se han explotado técnicas de inteligencia artificial en este campo, logrando resultados impresionantes que son casi perfectos (Bonello et al., 2018). Las técnicas de inteligencia artificial para pronosticar problemas financieros se hicieron comunes en los años 90, con el desarrollo de las técnicas informáticas (Paule-Vianez, 2019). El aprendizaje profundo ha surgido y está evolucionando progresivamente hacia una técnica robusta para diversos usos, y ha ayudado a resolver varios problemas en la economía y los negocios, como el reconocimiento de voz, el procesamiento del lenguaje natural, la conducción automática, la visión por computadora, la predicción de dificultades financieras y la evaluación del crédito (Qu et al., 2019).
Existen varios estudios científicos sobre el tema de las dificultades financieras y la predicción de quiebras, que han propuesto diversos modelos predictivos con ese fin. La mayoría de los estudios publicados utilizaron datos de un año antes de la crisis. Solo algunos estudios usaron datos de 2-3 años antes de la crisis. Los resultados mostraron que los datos que corresponden a dos años antes de crisis redujeron la capacidad del modelo para predecir dificultades financieras (Fernández-Gámez et al., 2016), con precisiones de 72,0 % y 95,5 %, 86,2 %, 100 % utilizando algoritmos genéticos y red neuronal de uno, dos y tres años antes del hecho. Algunos autores compararon la precisión de clasificación de los modelos de pronóstico basados en empresas industriales polacas. Mediante programas de R, la investigación probó redes neuronales, regresión logística, máquinas vectoriales de apoyo, árboles de clasificación, algoritmos k-NN, ensacado, bosques aleatorios, análisis discriminatorio, potenciación y Bayes ingenuos (Costa et al., 2022). Otros autores han estudiado varios modelos inteligentes y estadísticos, como la optimización de enjambres de partículas integrada en las máquinas virtuales semiconductoras, los árboles de decisión, el discriminante lineal y los algoritmos genéticos, utilizando regresión logística de las máquinas virtuales semiconductoras, mapas auto-organizados y cuantificación de vectores de aprendizaje. Los resultados muestran que las técnicas estadísticas son más adecuadas para grandes conjuntos de datos, y las técnicas inteligentes son más adecuadas para conjuntos de datos más pequeños (Zhou et al., 2019). Este método mejorado combina características de conjuntos difusos, y el aprendizaje automático se puede comparar con las redes neuronales probabilísticas en términos de rendimiento de agrupamiento. El objetivo del estudio consiste en predecir la decadencia mediante el método GP y su posterior comparación con máquinas de regresión logística y vectores de soporte. La investigación se basa en datos precisos sobre quiebras, y concluyó que los procesos gaussianos superan a otros métodos en la predicción de la quiebra con alta precisión (Liu et al., 2023).
El objetivo de este estudio es establecer una idea general de las ventajas que se pueden aplicar a los diversos actores, tanto académicos como profesionales. La economía de un Estado funciona como un sistema interconectado que abarca numerosos factores que contribuyen al establecimiento de una sociedad sólida y próspera. Si alguno de estos factores no cumple con sus objetivos, se producirá el fracaso de todo el sistema. Dado que las empresas económicas desempeñan un rol fundamental en la economía de un país, resulta necesario garantizar su continuidad por todos los medios posibles. En consecuencia, la importancia de predecir las dificultades financieras surge como un método basado en el avance de técnicas estadísticas e inteligentes que ayudan a las empresas a evitar el quiebre y el cese de sus operaciones.
Nuestro trabajo destaca entre el limitado número de publicaciones científicas que abordan este tema, distinguiéndose por su enfoque en la predicción de dificultades financieras utilizando el modelo GPR, por lo tanto, se realizaron pruebas preliminares sobre el modelo GPR. Nuestro objetivo principal es mejorar la investigación académica y hacer contribuciones significativas a su avance. Para esta investigación se definieron dos preguntas de investigación: ¿Es el modelo GPR adecuado para predecir las dificultades financieras? ¿Se contrapone el modelo GPR con el modelo de regresión logística para predecir las dificultades financieras?
El artículo se estructura de la siguiente manera. En la sección 1 se presenta una breve revisión de la literatura, en la sección 2 se proporciona información sobre el procedimiento de investigación, los datos y las variables, en la sección 3 se presentan los resultados obtenidos, en la sección 4 se analizan los resultados obtenidos y se ofrece un resumen general de los resultados de la investigación, incluidas las recomendaciones propuestas.
Metodología
Datos y variables
Este conjunto de datos abarca dos tipos distintos de variables. En primer lugar, está la variable independiente X, que es una variable cuantitativa que engloba un rango de 83 ratios financieros. Lamentablemente, los nombres específicos de estas relaciones no se proporcionaron de forma explícita; en su lugar, se denominaron X1, X2, ..., X83. Si bien esta falta de identificación precisa es un inconveniente, se optó por utilizar estos datos debido a su alineación con el objetivo principal del estudio, que implica evaluar la capacidad predictiva del modelo para dificultades financieras posteriores a la optimización de sus hiperparámetros. La identificación del conjunto de ratios financieros que ejercen la mayor influencia sobre la variable dependiente sirvió como objetivo secundario, especialmente después de la aplicación de la técnica PCA para mejorar la calidad de los datos.
El segundo tipo de variables corresponde a la variable dependiente, denominada Y, que es una variable cualitativa que representa las salidas del modelo y abarca dos escenarios fundamentales: dificultades financieras, que se denominan 0, y dificultades no financieras, que se denominan 1. Estos datos ofrecen una descripción precisa de las circunstancias reales de todos los casos financieros, teniendo en cuenta la importancia de los indicadores (83). En consecuencia, este conjunto de datos nos permite entrenar efectivamente el modelo y evaluar su capacidad predictiva.
Nos basamos en un conjunto de datos ya establecidos que incluye datos de 352 empresas extraídas de la base de datos de Kaggle. Dividimos estos datos en una muestra de capacitación y una muestra de prueba, donde la muestra de capacitación contenía los datos de 187 empresas para diferentes años, y el número de casos financieros (años fiscales) alcanzó 2001 casos financieros divididos en 896 casos de dificultades financieras y 1105 casos de dificultades no financieras, mientras que la muestra de prueba incluyó los datos de 165 empresas para un período de cuatro años, donde se excluyeron los datos del resto de años. El número de casos financieros (ejercicios fiscales) en la muestra de prueba alcanzó los 660 casos financieros, divididos en 351 casos de dificultades financieras y 309 casos de dificultades no financieras. En cuanto a los predictores utilizados en este estudio, se incluyen 83 ratios financieros, que representan un número considerable de variables independientes, lo cual es deseable, ya que nos ayudará a extraer los componentes más influyentes en la variabilidad dependiente después de activar la técnica de Análisis de Componentes Principales (PCA). En el cuadro 1 se muestran las variables más importantes en las que se basa este estudio.
Métodos
En este estudio se utilizó una metodología descriptiva en la sección teórica, recurriendo a fuentes acreditadas y revisadas por pares de revistas académicas indexadas. Por otro lado, la sección aplicada tuvo un enfoque comparativo utilizando un método analítico. Se realizaron dos indagaciones primarias, y luego de extraer los resultados relacionados con la mejora de la calidad del modelo de GPR, se hizo una comparación con modelos de aprendizaje profundo. Las conclusiones se debatieron a fondo y se abordaron las principales investigaciones.
El Matlab se utilizó para construir el modelo, optimizando sus hiperparámetros y poder mostrar los gráficos resultantes. Se utilizó Excel para calcular las medidas de error (MSE, RMSE, MAE), así como para determinar los elementos de la matriz de confusión (Sensibilidad, Especificidad, Precisión). Se empleó el SPSS para realizar la prueba estadística R2. La evaluación estadística del modelo se realizó utilizando la medida R2, la cual es ampliamente considerada como una de las pruebas estadísticas más significativas debido a su capacidad para evaluar la correlación entre los valores reales y los predichos. No se realizaron pruebas estadísticas adicionales, a excepción de la prueba R2, ya que el investigador creía que la prueba R2 capturaba adecuadamente la significación estadística del modelo. Además, cabe señalar que el PCA se consideró ineficaz. El modelo fue sometido a una evaluación matemática utilizando diversas medidas matemáticas significativas, incluyendo MAE, RMSE y MSE, para cuantificar el error del modelo. Adicionalmente, la evaluación involucró el examen de la matriz de confusión y sus métricas asociadas, tales como Exactitud, Sensibilidad y Especificidad. Estas medidas se emplearon para comparar el desempeño del modelo GPR con el de los modelos de aprendizaje profundo.
El alcance temporal y espacial de este estudio no están disponibles, y como se indicó previamente, estos datos se extrajeron de la base de datos de Kaggle, y están disponibles en el siguiente enlace: https://bit.ly/3DZxGr1. Lamentablemente, a pesar de la importancia de estos dos aspectos, los datos de que se disponen no proporcionan información específica sobre el alcance temporal y espacial. Sin embargo, debido a la necesidad de obtener resultados valiosos y significativos y a la ausencia de alternativas superiores, hemos optado por confiar en este conjunto de datos. El conjunto de datos es notable, ya que su propietario informa que posee los siguientes atributos: datos bien documentados, bien mantenidos, limpios y originales. Además, abarca un amplio intervalo temporal, aunque no se especifica el período exacto. Este alcance nos permite evaluar la capacidad predictiva de los modelos en el pronóstico de dificultades financieras cuatro años antes de su ocurrencia.
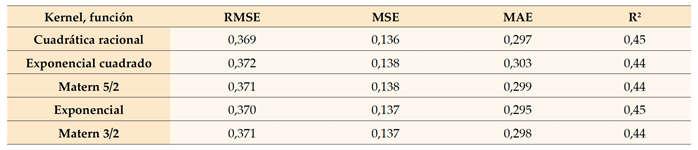
En la primera fase de este estudio se formulan cinco tipos de modelos GPR, cada uno distinguido por el tipo de función Kernel empleado. Posteriormente, estos modelos serán sometidos a entrenamiento utilizando la muestra de entrenamiento proporcionada, tras lo cual se realizará un análisis comparativo para identificar el modelo más óptimo que exhiba el valor mínimo de error. A continuación, el modelo seleccionado pasará a la segunda fase para su comprobación. Adicionalmente, tras la evaluación de este modelo, se formularán tipos adicionales de modelos utilizando la misma función Kernel que logró los mejores resultados en la fase anterior, pero variando en términos de la función base empleada. Una vez más, se llevará a cabo un proceso de selección para determinar el modelo más óptimo, que luego avanzará a la fase final que requiere comparar entre los modelos extraídos y los modelos de aprendizaje automático comúnmente utilizados.
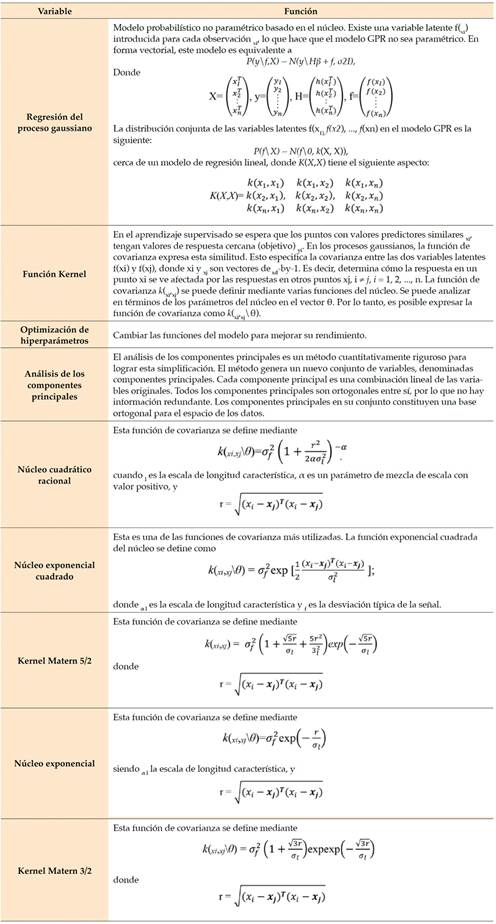
Al usar procesos gaussianos, se puede proporcionar un buen marco para la regresión de probabilidad (Yang et al., 2023). El método de proceso Gaussiano ha resurgido recientemente debido a la llegada de la inteligencia artificial y el aprendizaje automático basado en el núcleo. Estos modelos proporcionan diversos usos en varias áreas de la investigación y un método bayesiano no lineal completo (Antunes et al., 2017). El GPR es un modelo no paramétrico que depende de la distribución de probabilidad de Gauss y se define como un conjunto de variables aleatorias. Cada número finito GP de esta variable aleatoria tiene una distribución gaussiana común. Por lo tanto, el GP se especifica completamente por la estadística de segundo orden:
f(x) ~ GP(m (x), k (x, x′)) (1)
Donde m(x) y k(x,x′) son las funciones de covarianza y media de un proceso real f(x), respectivamente (Ferkousl et al., 2021). Solo define las funciones de covarianza y media para simplificar una función de un proceso gaussiano. La función de la covarianza k modela la variabilidad articular de las variables aleatorias del proceso gaussiano, y devuelve la covarianza modelada entre el par de entradas (Herfurth, 2020). El proceso gaussiano es un método robusto no paramétrico con modelos de incertidumbre precisos, utilizado principalmente en temas de clasificación y regresión. No es paramétrico porque el proceso gaussiano trata de inferir cómo todos los datos medidos están correlacionados en lugar de ajustar los parámetros de las funciones de base elegidas (Wang et al., 2023). Un proceso Gaussiano es un método de regresión probabilístico operativo, originalmente pionero en estadística y geofísica, que desde entonces ha encontrado una sólida base de usuarios en el aprendizaje automático. Un proceso gaussiano, considerado una técnica de regresión probabilística, toma un núcleo y un conjunto de datos como entrada y da la distribución de una función como salida (Asante-Okyere et al., 2018).
La GPR puede considerarse como una generalización de la regresión lineal bayesiana más estándar, y de manera similar, la clasificación del proceso Gaussiano puede considerarse como una generalización de la regresión logística. La activación de la función logística fue dada por a = wT φ (x). Por lo tanto, se puede permitir que los procesos gaussianos no linealicen la función manipulando directamente el espacio de funciones (Hamoudi et al., 2023). Por lo tanto, podemos reemplazar el modelo lineal wT φ (x(n)) con un proceso gaussiano f considerando el conjunto de variables latentes para n ∈ {1, N}. Además, estamos interesados en la probabilidad de pertenencia de π (x⋆) = p (y = 1| x⋆) = σ (f (x⋆)) dada una observación x⋆. El proceso de inferencia se realiza de forma similar al anterior, por lo que la distribución de f ⋆ se calcula como:
p (f⋆|D) = ʃ p (f⋆|D,f) p (f|D) ∂f (2)
Donde p (f|D) ∝ p (D|f) p(f) es la posterior obtenida mediante la aplicación de la regla de Bayes (Taki et al., 2018).
Debido a la función de la covarianza, hacer predicciones para nuevos puntos de prueba es sencillo, porque se trata de manipular matrices algebraicas. Sin embargo, en la aplicación procesal, puede ser necesario reconocer qué función de covarianza utilizar. Por supuesto, la confiabilidad de la regresión depende de qué tan bien se seleccionaron los parámetros requeridos por la función de covarianza elegida (Wang et al., 2023).
Resultados
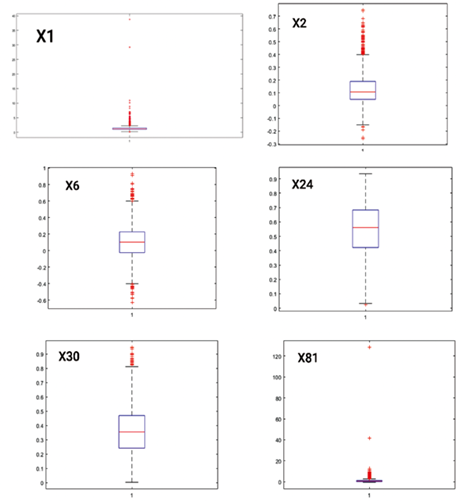
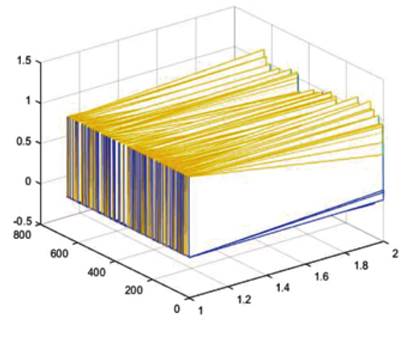
En esta sección, presentaremos los resultados obtenidos a través de la experimentación y discutiremos estos resultados con claridad. Después de haber organizado y distribuidos los datos en una muestra de capacitación y una muestra de prueba, procederemos a construir y desarrollar múltiples modelos para evaluar su capacidad para predecir dificultades financieras. Sin embargo, en primer lugar, se llevará a cabo un examen exhaustivo de los datos. Para ilustrar los datos se utilizan diagramas de cajas por varias razones. En primer lugar, los diagramas de cajas ofrecen información valiosa sobre la dispersión o variabilidad de los datos. En segundo lugar, proporcionan fiabilidad de la distribución de los valores. En tercer lugar, ayudan a identificar las regiones en las que los valores de la muestra están más densamente agrupados o son más escasos. Debido al gran número de variables independientes, concretamente 83, no es práctico crear un diagrama de caja independiente para cada variable. Por lo tanto, mostraremos selectivamente el diagrama de caja para un conjunto específico de variables, a saber, X1, X2, X6, X24, X30 y X81, elegidos al azar solo con fines ilustrativos. La figura 1 muestra los valores atípicos, representados en rojo, que se observan en dos áreas de la figura, ya sea que superen el valor máximo después de excluir los valores atípicos o que estén por debajo del valor mínimo después de excluir los valores atípicos.
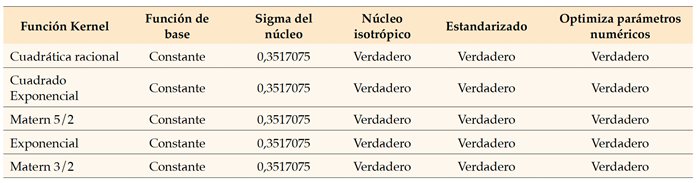
El cuadro 2 ilustra las características de diseño de los modelos GPR y ofrece una visión general clara de todos los detalles, como se indica a continuación.
El cuadro 2 presenta el objetivo principal de la investigación en el diseño de diversos modelos de GPR con el fin de comparar sus resultados e identificar el modelo más óptimo. Es importante resaltar que a lo largo de la fase de diseño, todos los parámetros permanecieron fijos y no se vieron afectados por las variaciones en el tipo de función Kernel. Además, se omitieron del análisis varios campos no esenciales, como la velocidad de predicción y el tiempo de entrenamiento, ya que tuvieron menos importancia. Como se muestra en el cuadro 2, durante la primera fase, se utilizó la función PCA para extraer los componentes principales y reducir el número de predictores, debido a la incorporación sustancial de ratios financieros. Al usar esta técnica ampliamente reconocida e indispensable, se pueden eliminar efectivamente las variables que no contribuyen a los objetivos de la investigación y que dificultan el logro de predicciones precisas con respecto a las dificultades financieras. Los resultados obtenidos del entrenamiento de los modelos GPR posteriores a la activación de la técnica PCA se presentan en el cuadro 3.
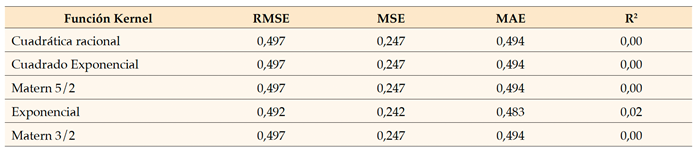
Para medir el valor de error se utilizaron los valores de raíz de error cuadrático medio (RMSE), error cuadrático medio (MSE) y error absoluto medio (MAE). Se empleó el coeficiente de determinación, denominado R2, como métrica estadística para evaluar la calidad del modelo y comprender la correlación entre las variables independientes y la variable dependiente, así como la correlación entre los valores observados y los valores predichos. Al analizar el cuadro 3, se observó que los resultados obtenidos podrían haber sido más satisfactorios. Sin embargo, estos resultados son inadecuados para ir a la segunda fase, es decir, a las “pruebas”. En esta fase, se observó que las medidas de precisión de predicción eran excesivamente elevadas y eran casi idénticas en todos los modelos. De igual forma, los valores de R2 fueron casi nulos para todos los modelos, indicando una falta de correlación entre los predictores y la variable dependiente, haciendo que los modelos sean estadísticamente insignificantes. Por lo tanto, esto sugiere la posibilidad de un desequilibrio producto del uso de la técnica de análisis de componentes principales (PCA), pero es contradictorio, ya que la técnica PCA normalmente contribuye a reducir el error y mejorar la calidad de la predicción. Por lo tanto, hay que investigar las causas de las medidas de error y la ausencia del coeficiente de determinación, por lo que el siguiente paso es descartar la técnica de PCA y evaluar si los resultados mejoran o empeoran. Posteriormente, en el cuadro 4, se descarta la técnica PCA, lo que arroja el siguiente conjunto de resultados.
Al analizar el cuadro 4, se observa una disminución notable de los valores de las medidas de precisión de la predicción, lo que sugiere una disminución de las tasas de error. Esto significa una mejora en la calidad de la predicción de los modelos, que se ve corroborada por el aumento sustancial de los valores de R2. Sin embargo, es importante señalar que estos valores no se acercaron a 1, sino que se mantuvieron considerablemente alejados de cero. En consecuencia, los modelos han alcanzado significancia estadística y pueden explicar efectivamente la relación entre los predictores y la variable dependiente con un coeficiente de correlación de 0,444. Por lo tanto, podemos inferir que el uso del Análisis de Componentes Principales (PCA) contribuyó principalmente al desempeño por debajo del estándar de los modelos. Al comparar las medidas de precisión de predicción, es evidente que el modelo inicial que utiliza la función de núcleo cuadrático racional presenta valores de error más bajos en comparación con los otros modelos, así como valores R2 más altos. Además, este modelo alcanza el nivel más alto de significación estadística. Por lo tanto, no tendremos en cuenta los modelos restantes y optaremos por emplear este modelo para realizar pruebas en la fase posterior. Los resultados de las pruebas del modelo cuadrático racional, basados en las mismas medidas mencionadas anteriormente, se presentan en el cuadro 5.
En el cuadro 5 se muestran los resultados obtenidos tras probar el modelo cuadrático racional utilizando la muestra de prueba. Se observó que las medidas de precisión de la predicción aumentaron en comparación con la fase de capacitación, lo que era de esperarse. Por otro lado, resulta positivo porque los valores de error aumentaron solo ligeramente, y esto indica que el modelo fue capaz de construir la fórmula adecuada que sirva al objetivo del estudio, y esto se puede confirmar por la tasa de precisión de predicción del 80 %, que es una tasa muy apropiada y refleja la fortaleza del modelo en la predicción de dificultades financieras. Para aclarar aún más los resultados de la prueba del modelo, nos basaremos en la figura 2 y el cuadro 6 para proporcionar información más detallada.
Se evaluó la precisión del modelo para predecir las dificultades financieras en diferentes momentos: un año antes de que se produjeran, dos años después, tres años después y cuatro años después. Cabe destacar que los valores de error fueron más altos en el primer año, junto con una clara disminución en el valor R2, lo que resulta inquietante pues se esperaba que el desempeño del modelo de clasificación en el año inicial fuera superior a los años subsiguientes, y luego comenzara a disminuir gradualmente, sin embargo, la calidad de la predicción mejoró cuanto más lejos se encontraba la posibilidad de que se produjera la crisis. Por lo tanto, se puede decir que el modelo es prometedor porque logró resultados relevantes, y por lo tanto optimizaremos los hiperparámetros del modelo para mejorar los resultados. Matlab nos permite realizar varias modificaciones en la fase de diseño del modelo y antes de entrenarlo. Tal vez una característica esencial que se puede modificar está relacionada con la función principal porque hemos hecho varias otras modificaciones. Sin embargo, sin obtener resultados deseados, por lo que no es necesario comentar sobre estas modificaciones. Como se muestra en el cuadro 7, el programa ofrece tres tipos de funciones de base, lo que permite la construcción de tres nuevos modelos de GPR basados en estas funciones. Sin embargo, solo se crearán dos nuevos modelos, ya que el modelo cuadrático racional que utiliza la función de base constante ya se ha construido en la fase anterior.
Los resultados de capacitación del modelo de relaciones lineales arrojaron resultados insatisfactorios, por lo que se omiten. Con base en los resultados de entrenamiento de los dos modelos restantes, se observa que tanto los valores de error como los valores de R2 muestran convergencia, aunque el modelo Cero ha mostrado un desempeño ligeramente superior. Estos hallazgos nos llevan a la fase de prueba y al análisis comparativo de los dos modelos, ya que los resultados de la capacitación han indicado el potencial para mejorar la precisión del modelo cuadrático racional. Los resultados descritos en el cuadro 8 presentan los siguientes resultados.
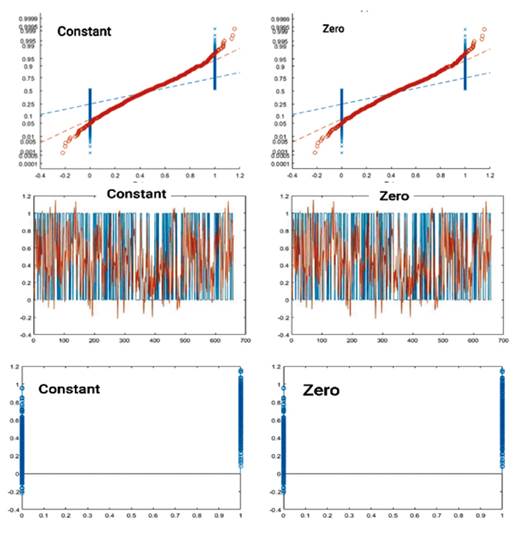
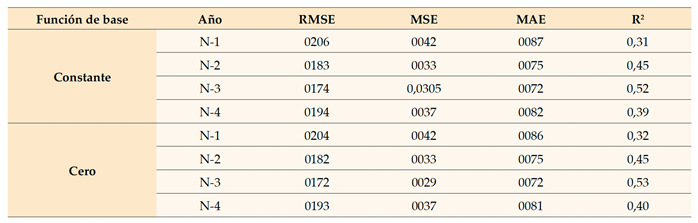
Cabe señalar que el modelo RQ-Cero mostró un rendimiento superior en comparación con el modelo RQ-Constante en todas las métricas presentadas en el cuadro 7. Por lo tanto, los resultados han mejorado, aunque marginalmente. Para obtener una visión más completa de los resultados de las pruebas para ambos modelos, utilizaremos la figura 3 y el cuadro 9 para presentar información más compleja y detallada. Presentamos las cifras de los modelos Constant-GPR y Zero-GPR, porque los resultados de estos dos modelos resultaron valiosos en comparación con los modelos anteriores. Esperamos aclarar la diferencia entre los dos modelos a través del gráfico residual, pero como se observa, la figura 3 no muestra una diferencia significativa entre los dos modelos debido a la convergencia de los resultados.
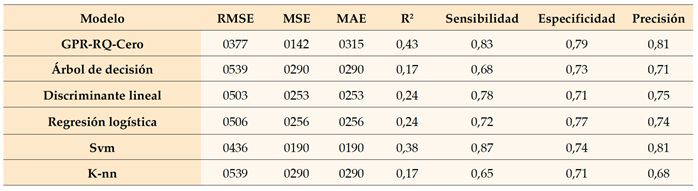
De acuerdo con los datos presentados en el cuadro 9, toda la evidencia disponible sugiere la superioridad del modelo RQ-Cero. Vale la pena señalar que un problema similar encontrado en el primer modelo también ocurrió en el modelo RQ-Cero, donde los valores de error fueron más altos en el primer año. Esta tendencia también puede observarse en el valor R2, ya que se preveía que la capacidad de clasificación del modelo sería mayor en el primer año y disminuiría gradualmente en los años siguientes. En este caso se observó lo contrario. En la etapa final, una vez identificado el modelo óptimo a partir de los modelos GPR, se procedió a comparar este modelo seleccionado con modelos de aprendizaje profundo como el modelo del árbol de decisiones, discriminante lineal, regresión logística, máquina de vectores de soporte y K-vecino más cercano.
Este resultado fue inesperado, particularmente en el contexto de la comparación del modelo de GPR con los modelos de aprendizaje profundo comúnmente utilizados para clasificar. Cabe destacar que el modelo RQ-Cero demostró un mejor rendimiento, situándolo a la vanguardia de los rankings junto al modelo Svm. Este logro es significativo, ya que los modelos RQ-Cero han demostrado su capacidad para aprender efectivamente y lograr resultados de clasificación apropiados. Además, se han observado ligeras distinciones entre los modelos Svm y RQ-Cero, lo que dificulta la determinación del modelo óptimo entre ellos, especialmente debido a la precisión de clasificación equivalente que muestran.
Discusión y conclusión
Se encontró que resulta necesario realizar más encuestas que se centren en la predicción de dificultades financieras utilizando el método de regresión de Gauss. Por esta razón, el siguiente texto se centrará en los resultados de las encuestas dedicadas a predecir la crisis financiera de la empresa a través de diversos métodos. En primer lugar, podemos mencionar el estudio de Jeong y Kim (2022), que diseñaron un modelo para predecir las dificultades financieras de las empresas constructoras, considerando tres, cinco y siete años antes del punto de predicción. Para construir el modelo de predicción, eligieron la razón financiera como variable de entrada adicional, adoptada en estudios existentes de predicciones de mediano a largo plazo en otras industrias. Analizaron el desempeño de modelos monomáquicos y de ensamble para comparar el desempeño de modelos de predicción. Esta comparación se basó en el valor promedio del rendimiento de la predicción y los resultados de la prueba de Friedman. El desarrollo de la comparación determinó que el modelo del subespacio aleatorio (RS) mostró el mejor desempeño en la predicción de la situación financiera de las empresas constructoras en el mediano a largo plazo.
Rahman et al. (2021), a su vez, investigaron la aplicación de un modelo predictivo de dificultades financieras, que utiliza el método de puntuación F incluidos sus componentes, con el fin de identificar a las empresas con un alto riesgo de fracaso. El conjunto de datos se creó sobre la base de datos de investigación de quiebres de UCLA-LoPucki, donde 81 empresas estadounidenses con cotización oficial en dificultades financieras fueron monitoreadas específicamente durante el período 2009-2017. La encuesta concluyó que la relación entre la puntuación F y la probabilidad de que una empresa sufra dificultades financieras es significativa. Entre otras cosas, los resultados también muestran que las empresas en crisis tienen un flujo de caja negativo de las operaciones (CFO) y muestran una disminución más significativa en la rentabilidad de los activos (ROA) en el año anterior al quiebre.
Como parte de su investigación, Chen y Shen (2020) aplicaron métodos híbridos de aprendizaje automático que integran árboles de regresión escalonada, regresión y clasificación, selección y el operador de encogimiento menos absoluto, y bosques aleatorios, y utilizaron todos estos métodos para crear modelos con los que será posible predecir las dificultades financieras de la empresa. Para la investigación se utilizaron un total de 14 variables financieras y seis variables no financieras. Los resultados muestran que el modelo CART-LASOO tiene el mayor nivel de precisión, concretamente el 89,74 %. También se puede mencionar el estudio de Chen y Du (2009), que utilizaron la minería de datos y la agrupación de redes neuronales para predecir las dificultades financieras, aplicando 33 variables de carácter financiero y cuatro variables de carácter no financiero. Las conclusiones del estudio muestran que los modelos diseñados con redes neuronales artificiales logran una mejor precisión. Con el fin de predecir dificultades financieras, el método de Gregorova et al. (2020) - LR (regresión logística), RF (bosques aleatorios) y NN (redes neuronales), usaron 14 ratios financieros y obtuvieron el mejor desempeño en el modelo NN con un resultado de precisión de 88,6 %. Chen y Jhuang (2020), que también utilizan los métodos ANN y CHAID, SR-C5.0, fueron responsables de otro modelo utilizado para predecir dificultades financieras. Los autores usaron 18 variables de carácter financiero y tres variables no financieras, y encontraron que el modelo SR-C5.0 presentó el mayor nivel de precisión. La tasa de precisión global fue del 91,65 %. El objetivo principal del estudio de Jan (2021) fue crear modelos altamente eficientes y precisos que sean capaces de predecir la dificultad financiera utilizando redes neuronales profundas (DNN) y redes neuronales convolucionales (CNN). Con base en los resultados, los autores concluyeron que la tasa de precisión más alta de la predicción de dificultades financieras es del 94,23 % y la tasa de error más baja de tipo I y la tasa de error de tipo II son del 0,96 % y el 4,81 %, respectivamente.
Gracias a los resultados anteriores, ahora es posible proceder con las respuestas a las preguntas de investigación.
¿Es el modelo GPR adecuado para predecir dificultades financieras?
Aunque, según el análisis de la literatura existente, el modelo de GPR no es una herramienta ampliamente utilizada en la práctica para las dificultades financieras, los resultados de esta encuesta muestran que el modelo de GPR es excelente para estas necesidades. Esto se debe principalmente a que el modelo logra resultados muy satisfactorios, con una precisión de clasificación del 81 %.
¿Se contrapone el modelo GPR con el modelo de regresión logística para predecir dificultades financieras?
Después de comparar los resultados de este modelo con los modelos de aprendizaje profundo, y el modelo de regresión lineal, se encontró que el modelo GPR superó a este modelo comúnmente utilizado. Como se mencionó anteriormente, el modelo GPR alcanzó una precisión de clasificación del 81 %, mientras que el modelo de regresión lineal alcanzó solo el 74 %.
En la primera fase se identificó el modelo más adecuado entre los modelos GPR comparando sus funciones Kernel y el modelo fue el RQ. En la fase posterior, enfocada a mejorar el desempeño del modelo a través de la optimización de hiperparámetros, se logró identificar el modelo óptimo a partir de los modelos GPR con base en la variación de la función Base, que se denominó RQ-Cero. Después de comparar los resultados de este modelo con los resultados de otros modelos de aprendizaje profundo, concluimos que el rendimiento del modelo fue excelente porque logró resultados muy relevantes, ya que superó a todos los otros modelos utilizados comúnmente con el modelo SVM, y esto nos lleva a plantearnos la siguiente pregunta, ¿por qué no se ha probado el modelo GPR en la predicción de dificultades financieras basado en la diferencia del tamaño y el tipo de muestra de prueba de una manera que lo hace comúnmente utilizado en la predicción de dificultades financieras o la predicción de quiebres? También se concluye que existe una relación inversa entre los valores de error y R2, ya que cuantos menores sean los valores de error, mayor será el valor R2, lo que indica la precisión y calidad del modelo en la predicción de dificultades financieras. Por otro lado, la técnica PCA no logró el objetivo deseado, ya que se logró una mejora en los resultados después de deshabilitar esta técnica. Finalmente, se recomienda probar el modelo GPR en la predicción de dificultades financieras con base en una muestra de estudio diferente.
Los hallazgos de esta investigación subrayan la importancia de predecir las dificultades financieras mediante el uso del GPR, que ha demostrado una gran capacidad para una predicción precisa, particularmente cuando sus hiperparámetros son optimizados. Este modelo ha demostrado un rendimiento superior en comparación con otros modelos de aprendizaje profundo y está a la par con las máquinas vectoriales de soporte (SVM), que en sí mismo es un logro digno de mencionar. Hasta donde sabemos, la GPR es una técnica poco utilizada en el contexto de la predicción de dificultades o quiebres. Por lo tanto, este estudio pretende alterar las perspectivas de los investigadores sobre la utilización de la GPR en este dominio. Mediante la exploración de nuevas variaciones de los modelos de GPR y su sometimiento a nuevas y diversas muestras de estudio, es posible identificar y abordar las limitaciones de investigaciones anteriores, incluyendo el presente estudio. Tales esfuerzos pueden ampliar los resultados y beneficios para todos los interesados involucrados en este tema, incluyendo prestamistas, auditores, inversionistas, entidades gubernamentales y, en particular, empresas, debido a que la continuidad de una empresa está interconectada con la estabilidad general de la economía del Estado. Predecir con precisión las dificultades financieras de una empresa facilita el mantenimiento de la prosperidad, minimiza las pérdidas, aumenta las tasas de inversión, preserva las oportunidades de empleo, evita los despidos y mantiene un entorno mutuamente beneficioso para todas las partes involucradas.