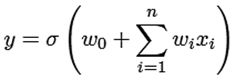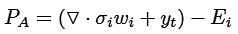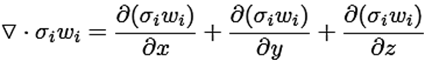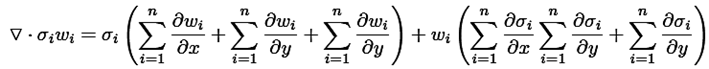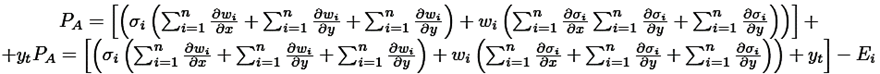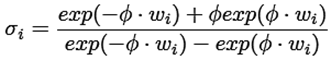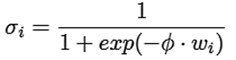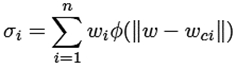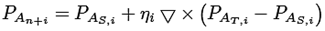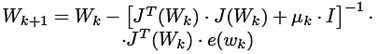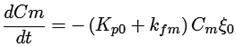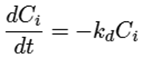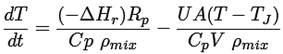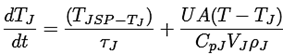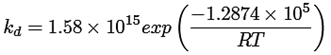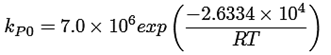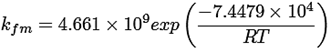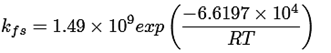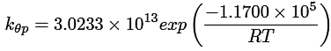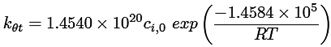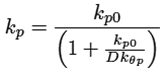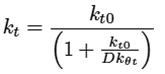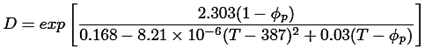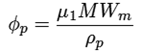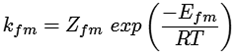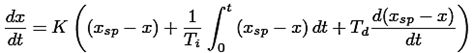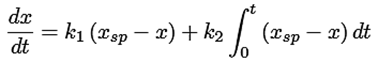Introducción
Las redes neuronales artificiales son sistemas basados en las capacidades cognitivas y de resolución de problemas del cerebro humano. Sin embargo, la robustez de las redes neuronales artificiales es mayor que la del cerebro humano. Los sistemas basados en inteligencia artificial y redes neuronales artificiales (RNA) presentan un sobreaprendizaje de la dinámica del proceso, característica que se asemeja a la adaptabilidad del cerebro humano [1-4].
Existen diversos tipos de redes neuronales y la elección de un tipo específico depende de las características deseadas de la red y de los requisitos particulares del proceso. Por consiguiente, la red que ofrece una mayor robustez suele ser la configuración más adecuada. Sin embargo, al igual que el cerebro humano [5-9], las redes neuronales artificiales también pueden mostrar un aprendizaje no ajustable, conocido como sobreaprendizaje. Como parte de su ajuste, la red neuronal utiliza valores calculados que no representan con exactitud el sistema, lo cual es un aspecto crucial para la investigación sobre redes neuronales artificiales. La búsqueda de una red neuronal capaz de mitigar el sobreaprendizaje ha traído consigo el desarrollo de diversas redes neuronales artificiales. Estos nuevos tipos de redes neuronales combinan distintas técnicas de inteligencia artificial, como la lógica difusa, los algoritmos evolutivos y las técnicas de optimización (métodos estocásticos), con el fin de mejorar la respuesta y el rendimiento general de la red neuronal [10-14].
Una red neuronal artificial se puede utilizar para el reconocimiento de patrones e imágenes o como controlador. En este trabajo, se utiliza una red neuronal artificial combinada con una técnica de evolución para crear una red neuronal artificial evolutiva, conocida como control neuroevolutivo [15].
En este estudio se realiza una comparación entre las funciones de excitación utilizadas en los controladores neuroevolutivos y los controles convencionales, como el PID y el GMC. Los resultados obtenidos demuestran que los sistemas basados en inteligencia artificial y redes neuronales evolutivas proporcionan un mejor ajuste que los sistemas de control tradicionales, como el PID, así como los no convencionales, como el GMC. Este estudio resalta un nuevo aspecto de la aplicación de sistemas inteligentes en el control de procesos con dinámicas impredecibles [16-18].
Materiales y métodos
Las características de un controlador de red neuronal evolutiva se centran en una red neuronal artificial que incluye una función de representación neuronal basada en los pesos de entrada (valores x i ) y una función de excitación σ. Esta última función permite propagar los pesos a los valores máximos y mínimos [19-22] (véase ecuación (1)).
(1)
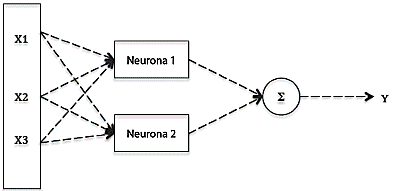
Donde w 0 representa el valor del peso inicial, el cual puede reemplazar el papel de la función de excitación (σ) para minimizar el error y así evitar el sobreaprendizaje. La Figura 1 muestra el esquema de la estructura principal de una red neuronal artificial.
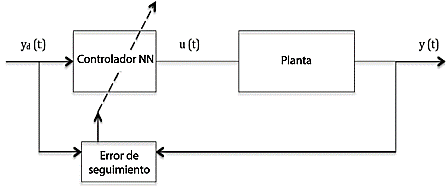
El controlador de red neuronal no requiere la linealización del modelo de acuerdo con una ley matemática de control determinada. Esto se debe principalmente a que la red neuronal artificial primero linealiza el modelo evolutivo para representar adecuadamente la dinámica del proceso. La Figura 2 muestra el funcionamiento de un controlador de red neuronal [23].
La respuesta del control basado en redes neuronales evolutivas emplea algoritmos evolutivos que sientan las bases de la evolución de la red neuronal y modifican la red neuronal básica.
Cuando se emplean los tres métodos de evolución en una red neuronal, es necesario comprender que la red neuronal funciona de forma dinámica. En este caso solo se utilizan las dos primeras técnicas de evolución y esto se debe principalmente a que se emplea una red neuronal estática. La red neuronal no modifica sus pesos estáticos ni sus interconexiones neuronales, sino que evoluciona generando nuevas neuronas para almacenar información [24].
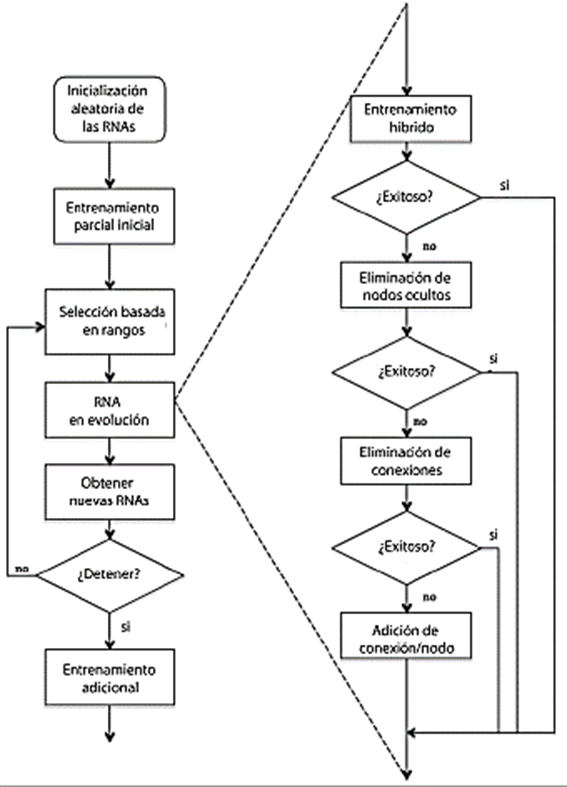
La implementación de las técnicas en una red neuronal evolutiva implica utilizar un algoritmo evolutivo siguiendo una serie de pasos establecidos. La Figura 3 representa las etapas secuenciales involucradas en la creación de la estructura de una red neuronal artificial evolutiva. La etapa inicial del proceso de estructuración se basa en la obtención de los pesos sinápticos, los cuales pueden adquirirse mediante un proceso supervisado o no. En el caso de modelos no lineales como los reactores de fermentación, los valores se obtienen a través de un algoritmo no supervisado que se basa en las variables del modelo matemático (T, P, crecimiento de la levadura, concentración, etc.) obtenidas a partir de la solución. Teniendo en cuenta el modelo matemático, los pesos se utilizan en el proceso de entrenamiento de la red neuronal, que se combina con el algoritmo de evolución. Este ciclo se repite hasta encontrar la estructura más adecuada (fenotipo de la red neuronal evolucionada), lo que indica que el sistema puede seguir evolucionando. Si las variables de control experimentan perturbaciones, se realizan los ajustes mediante el proceso evolutivo de la misma estructura de la red neuronal artificial evolucionada. Esto se consigue mediante la aplicación del método de evolución, que consiste en analizar los valores de los pesos entrenados para obtener una nueva generación de neuronas evolucionadas que puedan adaptarse eficazmente a la dinámica del sistema y lidiar con las perturbaciones [25].
La configuración de un sistema de control mediante el uso de redes neuronales evolutivas comienza con la arquitectura de una red neuronal primaria. Esta arquitectura está formada por una neurona de entrada, una neurona en la capa oculta y una neurona en la capa de salida, y se configura basándose en el conocimiento previo de que la variable a controlar es únicamente la temperatura del reactor de polimerización [26].
Una vez creada, la arquitectura básica se establece como progenitora para cada neurona (ecuación (2)).
(2)
Donde σi representa la función de excitación, w i denota los pesos sinápticos (entrada), y t representa la serie temporal de pesos sinápticos propagados, y e i representa el error de entrenamiento.
Las expansiones de peso y la función de excitación se representan en las siguientes ecuaciones, las cuales muestran cómo los pesos pueden expandirse en tres dimensiones. Esto permite a la red neuronal propagar la información de una manera muy similar al funcionamiento del cerebro humano [14], (ecuación (3) y ecuación (4)).
El progenitor se representa como: (ecuación (5)).
(3)
(4)
(5)
El sistema se utilizó para estudiar tres funciones de excitación distintas: la función tangencial (ecuación (6)), la función logarítmica (ecuación (7)) y la función de base radial (ecuación (8)).
(6)
(7)
(8)
Donde ∑ i=1 n w i representa la pendiente de la función de excitación y w i los pesos de entrada de la red neuronal. Los pesos de entrada de la red neuronal artificial pueden obtenerse generalmente a partir de un modelo de referencia o a través de los datos experimentales del sistema a comprobar.
La evolución de la red neuronal se logra utilizando la ecuación de reproducción del progenitor, que abarca los estados evolutivos y las técnicas para evolucionar (ecuación (9)).
(9)
Donde S y T representan cada uno de los progenitores seleccionados y ηi denota un número aleatorio uniforme entre cero y la unidad [15]. Para el entrenamiento de la red neuronal se utiliza el algoritmo de Levenberg-Marquardt (LM). Este método de entrenamiento acelerado es capaz de funcionar simultáneamente como un entrenamiento por descenso de gradiente y como un entrenamiento Quasi-Newton (BFGS). El entrenamiento LM utiliza el método Newton, que se basa en la expansión de la serie de Taylor de segundo orden para obtener la matriz Hessiana de los pesos de la red. Después de obtener la matriz hessiana, se aproxima una matriz jacobiana, siguiendo varios pasos de entrenamiento [26]. El método LM con el factor de escala μk se puede expresar de la siguiente manera (ecuación (10)):
(10)
Donde J (wk) representa la matriz jacobiana, I representa la matriz de identidad y e (wk) denota el error de peso sináptico.
El modelo de redes neuronales se aplica al modelo evolutivo de un reactor de polimerización que utiliza radicales libres de metilmetacrilato (MMA) para producir polimetilmetacrilato (PMMA). El modelo matemático incluye balances de masa, energía y ecuaciones cinéticas. Este modelo proporciona un enfoque directo para implementar el control mediante redes neuronales, lo cual aplica también para las reglas necesarias para obtener las leyes de control de los controladores GMC y PID [27].
Balance de masa, ecuaciones (11) y (12):
(11)
(12)
Balance de energía, ecuaciones (13) y (14):
(13)
(14)
Ecuaciones cinéticas ((15) a la (25))
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
La implementación de un sistema de control basado en inteligencia artificial (IA), como las redes neuronales artificiales evolutivas, difiere de los sistemas de control convencionales porque solo requiere de entrenamiento y conocimiento del comportamiento de las variables del proceso a controlar. En el caso de un reactor de fermentación, los factores principales que se deben tener en cuenta son la temperatura, la cinética de crecimiento de los microorganismos y la concentración del producto final de la fermentación. Este planteamiento desafía los paradigmas de ajuste tradicionales de los sistemas de control convencionales. Es crucial garantizar que el sobreaprendizaje no se produzca repetidamente. Esto puede lograrse aplicando un algoritmo de entrenamiento autoajustable que se adapte a la dinámica del propio proceso fermentativo.
Las siguientes ecuaciones describen las leyes de control para el controlador PID convencional y el controlador GMC menos convencional [18]. Los métodos clásicos o heurísticos para determinar los parámetros de control PID fueron introducidos por Ziegler y Nichols en 1942. Estos métodos han tenido un impacto significativo en la práctica y continúan siendo una referencia en la actualidad, a pesar de no brindar un ajuste óptimo. Estos métodos se basan en la caracterización de la dinámica del proceso utilizando dos parámetros para determinar los parámetros del controlador PID.
El método de respuesta en frecuencia se implementó para caracterizar la dinámica del sistema en lazo cerrado utilizando únicamente la acción de control proporcional. El proceso involucra incrementar la ganancia proporcional, Kp, comenzando desde cero hasta que el sistema exhiba oscilaciones sostenidas en la salida.
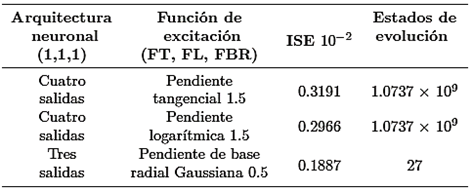
Este enfoque lleva al sistema al límite de la estabilidad. Los parámetros que caracterizan la dinámica del sistema son Ku, la ganancia proporcional a la que se producen oscilaciones sostenidas, y Tu, el periodo de oscilación correspondiente. Una vez determinados estos parámetros, se pueden obtener los parámetros del controlador PID utilizando la Tabla 1 [19].
Control PID: Ecuación (26).
(26)
Control GMC: Ecuación (27).
(27)
Resultados y discusión
El objetivo del entrenamiento de una red neuronal es determinar los parámetros de linealización del modelo matemático. En el caso del reactor de polimerización, la Figura 4 ilustra el proceso de linealización del modelo matemático a través del entrenamiento de la red neuronal evolutiva. Durante la fase inicial de entrenamiento, se generan secuencialmente los parámetros que guían la evolución de la red.
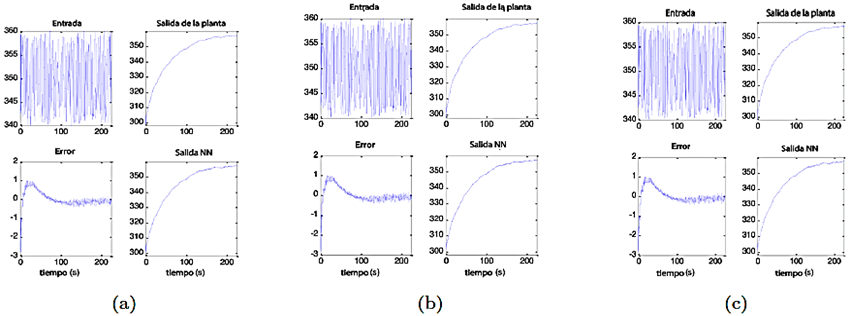
Figura 4 Respuestas de planta y RNAE (a) Función logarítmica, (b) Base radial gaussiana, (c) Función tangencial
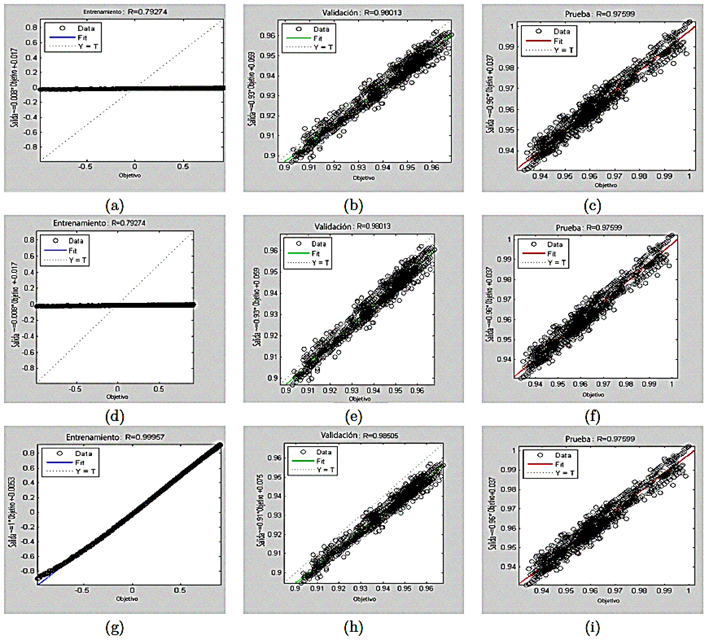
Los gráficos de entrenamiento, validación y prueba de la Figura 5 ilustran las principales tendencias de la red neuronal evolutiva. Específicamente, la Figura 5a muestra el proceso de entrenamiento para la función tangencial, que presenta un patrón de convergencia similar al de la función logarítmica (Figura 5d) con un valor de 0,79274. Por otro lado, el entrenamiento de la función radial gaussiana converge a un valor de 0,99957, lo que indica que esta función tiene una menor tendencia al sobreaprendizaje (Figura 5g).
Los gráficos de validación y prueba muestran un comportamiento similar para las tres funciones.
Los resultados obtenidos de la red neuronal evolutiva se presentan en la Tabla 1, la cual muestra la arquitectura de la red neuronal artificial y el estado evolutivo para diferentes funciones de excitación. Es válido mencionar que las simulaciones se realizaron en Matlab, cambiando el número de salidas de la red neuronal en un rango de 2 a 4 salidas para cada neurona, mismas que se obtuvieron a partir de los estados evolutivos. Los estados de evolución proporcionan el número total de neuronas evolucionadas para el sistema
de control.
Una de las principales ventajas de implementar un sistema de control utilizando redes neuronales artificiales evolutivas es la capacidad de obtener estructuras neuronales simples que evolucionan según la dinámica propia del proceso. Esto significa que con un diseño básico (fenotipo neuronal), el sistema puede adaptarse a la dinámica y a las no linealidades sin necesidad de un entrenamiento constante, proporcionando un sistema de autoaprendizaje en bucle cerrado o abierto, que se adapta a los requisitos específicos del proceso a controlar. En cambio, los sistemas de control convencionales, como el PID, necesitan ser ajustados en un bucle cerrado, lo que puede tomar mucho tiempo para finalmente no adaptarse completamente a la dinámica del proceso.
Se analizaron las tres funciones de excitación con diferentes pendientes, valorando su influencia en la evolución de los estados. Además, se calculó el error cuadrático integral (ISE) para determinar qué red neuronal se ajusta mejor a la dinámica del proceso.
La Tabla 2 muestra el análisis del error cuadrático integral (ISE) de los dos controladores utilizados en la comparación (PID y GMC). Este análisis proporciona información crucial para establecer el ajuste óptimo de los controladores a la dinámica del proceso.
La estructura de la red neuronal seleccionada presenta errores mínimos. La red neuronal evolutiva con una función de base radial gaussiana con un valor de α = 0.5 arroja el menor número de estados de evolución, con un total de 27. Estos pocos estados de evolución indican que las redes neuronales añadidas no presentan sobreaprendizaje. Los errores se reparten eficazmente entre los pesos y se incorporan al proceso de entrenamiento. Además, la red neuronal está configurada con tres salidas, lo cual es una elección adecuada, ya que evita la formación de nuevas neuronas que podrían dar lugar al sobreaprendizaje.
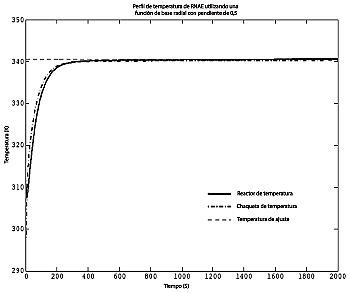
La Figura 6 muestra la respuesta del sistema de control neuronal utilizando la función de base radial gaussiana con tres salidas de red neuronal. Se puede observar que el sistema sigue adecuadamente el punto de ajuste en un corto período de tiempo sin generar una respuesta brusca, lo que indica un control efectivo por parte del controlador.
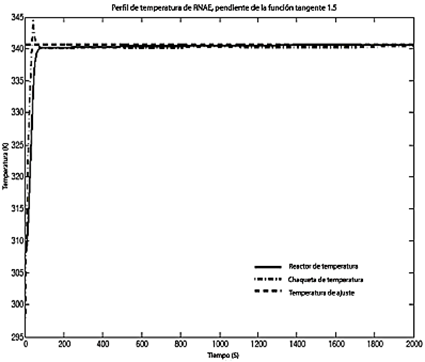
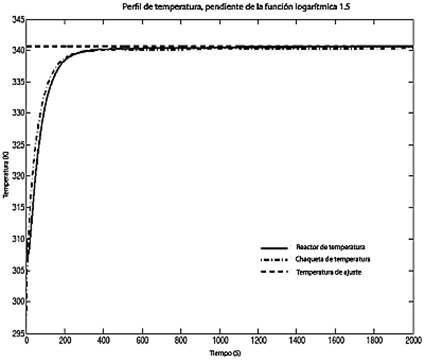
Las Figuras 7 y 8 muestran la respuesta del controlador para las otras dos funciones de excitación con diferentes pendientes y número de salidas, como se indica en la Tabla 1. La respuesta de la función de control tangencial con cuatro salidas exhibe un pico transitorio en la temperatura de la chaqueta, como se muestra en la Figura 7. Sin embargo, cuando se utiliza la función logarítmica con una pendiente de 1,5 y el mismo número de salidas, la respuesta de control está bien ajustada al punto de ajuste. Esta respuesta muestra un comportamiento similar a la respuesta obtenida con la función de base radial con una pendiente de 0,5. Es importante tener en cuenta que la función logarítmica presenta un mayor número de estados de evolución, lo que puede provocar un sobreaprendizaje en la red neuronal evolutiva.
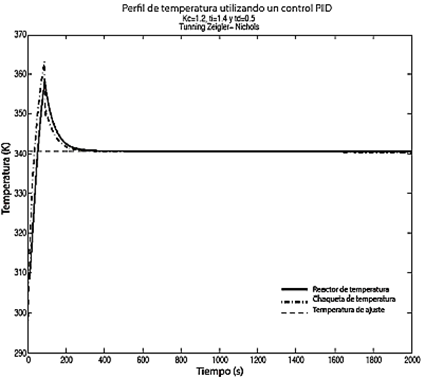
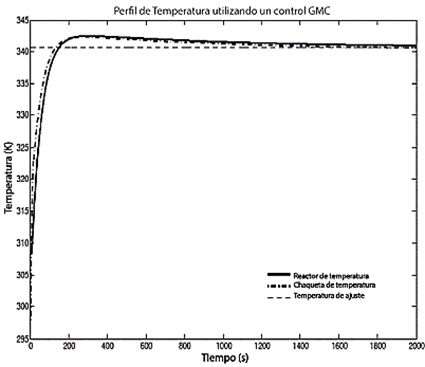
La respuesta del control PID se muestra en la Figura 9. Es válido mencionar que el control PID fue ajustado utilizando la técnica de Zeigler-Nichols [19] para cada una de las constantes del controlador. La respuesta del control PID muestra un sobreimpulso más significativo que el control con redes neuronales. Esto puede atribuirse principalmente a la técnica de ajuste, la cual tiende a aumentar el sobreimpulso. El control GMC también requiere de ajuste porque depende de una constante del controlador. La técnica de ajuste utilizada para el control GMC es la propuesta por Lee-Sullivan [18] y la respuesta del control GMC se muestra en la Figura 10. Comparado con el control PID, el control GMC no muestra un sobreimpulso significativo en su respuesta de control, lo cual confirma que la técnica de ajuste del controlador es sensible a la respuesta del sistema.
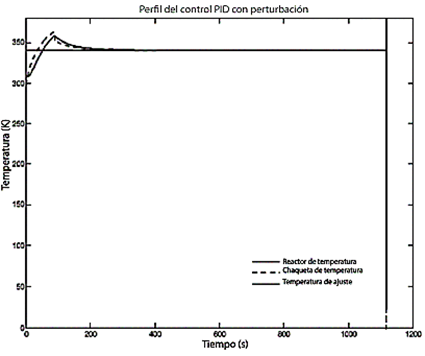
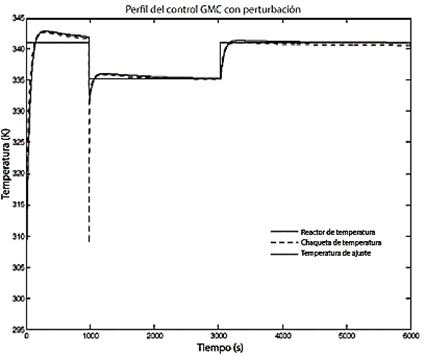
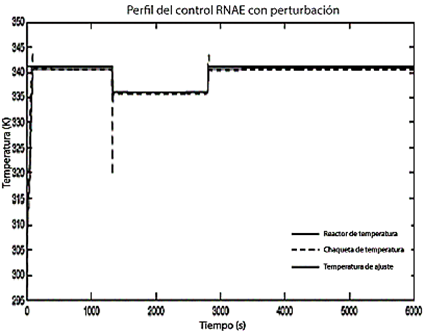
Además de minimizar el error cuadrático integral (ISE) en el control, es necesario considerar las perturbaciones que puedan surgir en el sistema para evaluar la capacidad de respuesta del sistema de control. En este estudio los tres sistemas de control: PID, GMC y RNAE se sometieron a dos perturbaciones: ajuste con el menor tiempo muerto (Td) y con una frecuencia mínima. La respuesta del controlador PID a la perturbación se caracteriza por un fallo en el retorno al punto de ajuste, provocando la inestabilidad del control, tal y como se muestra en la Figura 11. El control GMC presenta variaciones en la trayectoria de los cambios del punto de ajuste, tal y como se muestra en la Figura 12 . El control RNAE sigue el punto de ajuste secuencialmente sin ninguna variación, como se muestra en la Figura 13. Las perturbaciones demuestran la robustez del sistema de control, demostrando que las redes neuronales evolutivas con función radial gaussiana ofrecen mejores resultados que los métodos de control PID y GMC.
Conclusiones
Este estudio presenta un enfoque de control innovador basado en redes neuronales artificiales evolutivas. El sistema de control incorpora diferentes funciones de excitación y permite modificar el número de salidas de la red neuronal. El análisis de estas dos variables pone de manifiesto la tendencia evolutiva de la red neuronal. El reactor de polimerización utilizado en el caso de estudio para producir polimetilmetacrilato (PMMA) es un sistema dinámico que implica retos y desafíos para los métodos de control convencionales como el PID y otros enfoques menos tradicionales como el GMC. Aunque estos métodos pueden ofrecer resultados satisfactorios, se ven limitados por la necesidad de ajustes constantes del controlador. Sin embargo, el control basado en redes neuronales evolutivas supera esta limitación al adaptarse a la naturaleza dinámica del proceso sin requerir ajustes constantes. Además, el control basado en redes neuronales evolutivas logra reducir eficazmente el sobreimpulso en comparación con métodos de control convencionales como PID y GMC.
Con respecto a los diferentes tipos de funciones de excitación, resulta evidente que la función más compleja, la de base radial, genera una mejor respuesta del controlador basado en redes neuronales evolutivas. Al comparar el control basado en la función logarítmica con el de la función de base radial, se aprecia una diferencia notable en los estados de evolución minimizados. La función de base radial requiere menos salidas de la red neuronal, lo que se traduce en un menor número de estados de evolución. Esta es una característica significativa, ya que reduce la probabilidad de que la red experimente sobreaprendizaje. Por lo tanto, la función de base radial ofrece una ventaja al minimizar el riesgo de sobreaprendizaje, garantizando así una respuesta de control más efectiva.
Una opción viable para entrenar redes neuronales artificiales evolutivas es el aprendizaje profundo, el cual puede ser implementado utilizando un esquema de entrenamiento supervisado de redes neuronales. Este enfoque puede ser una alternativa para este tipo de sistemas, principalmente cuando se dispone de pesos suficientes para proyectar la dinámica del proceso. En este contexto, es posible utilizar estructuras arquitecturas neuronales simples en un proceso de entrenamiento supervisado. Además, la exploración de algoritmos de evolución de redes neuronales abre un camino prometedor para el control de procesos no lineales, proporcionando un nuevo y emocionante campo de estudio.