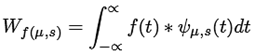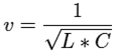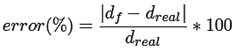Introducción
Las redes de distribución son las encargadas de suministrar energía eléctrica a los consumidores, utilizando un conjunto de elementos eléctricos tales como conductores, equipos, transformadores, protecciones y estructuras para su sujeción. En las redes de distribución existen muchos problemas ocasionados por las fallas eléctricas, por este motivo es de vital importancia conocer la ubicación de estas fallas. Las fallas pueden interrumpir el suministro de electricidad al consumidor final y hacer que la red sea inestable, reduciendo así la confiabilidad del sistema eléctrico. Todos estos problemas pueden provocar el incremento de pérdidas económicas a los consumidores, a las centrales eléctricas y a las distribuidoras de energía eléctrica [1].
De acuerdo con el estudio desarrollado en [2], más del 80 % de las interrupciones ocurridas en sistema eléctricos de potencia se deben a fallas que ocurren en los sistemas de distribución. Estas fallas son ocasionadas por muchas razones, entre estas se destacan rayos, fallas de los componentes del sistema de energía, debido al envejecimiento del equipo, y errores humanos [3]. Por lo tanto, las distribuidoras de energía eléctrica tratan de utilizar tecnologías eficientes, acciones de mantenimiento preventivas y procedimientos correctivos para reducir las tasas de fallas y sus efectos destructivos.
La adecuada ubicación de fallas eléctricas es uno de los problemas más críticos en el sistema de distribución de energía eléctrica. Localizar la falla eléctrica de forma óptima es esencial para ayudar al personal de mantenimiento eléctrico a dirigirse hacia el lugar de trabajo de forma ágil, garantizando así la reducción de los tiempos de búsqueda de la falla. Con esto se logra minimizar la duración de la interrupción, el tiempo de restauración de la energía y los costos operativos y de pérdidas comerciales por energía no suministrada a los clientes [4].
A pesar de los avances tecnológicos y la necesidad de mejorar el rendimiento y control de los procesos, en las empresas distribuidoras la mayor fuente de identificación de problemas y localización de fallas todavía siguen siendo las llamadas de los clientes afectados por las averías. Cuando ocurre una falla permanente, los gerentes del centro de operaciones identifican el alimentador y la posible zona de ocurrencia y luego se envía personal de mantenimiento a patrullar esa área para identificarla y aislarla. Este procedimiento es ineficaz en determinadas circunstancias porque el área de exploración puede ser considerablemente extensa [5].
Generalmente, se utilizan métodos basados en las componentes fundamentales de impedancia y frecuencia, ondas viajeras, conocimiento, entre otros [6], para diagnosticar y localizar fallas en los sistemas de distribución. El primer método requiere datos de medición de voltaje y corriente a frecuencia fundamental para determinar la impedancia y estimar la ubicación de la falla, usando uno o varios puntos de medición. Este método tiene la ventaja de ser implementado a bajo costo. Aun así, tiene la desventaja de estimar múltiples ubicaciones de fallas debido a la gran cantidad de ramales que puede tener una red de distribución [7]. La técnica del conocimiento abarca métodos basados en análisis y estadísticas, dispositivos de distribución, inteligencia artificial y métodos híbridos. La aplicación del método de conocimiento requiere mediciones de voltaje y corriente en el alimentador, el estado de operación de la subestación y el interruptor del alimentador, y datos proporcionados por dispositivos electrónicos inteligentes (IED) y dispositivos de protección instalados en los alimentadores [8]. El método de ondas viajeras para localización de fallas en sistemas de distribución, que se utilizará para este trabajo, se basa en la transmisión y reflexión de ondas viajeras entre los terminales de la línea y el punto de falla. Este método requiere dispositivos electrónicos inteligentes (IED) y dispositivos de protección capaces de almacenar información de corriente y voltaje de operación de la red para obtener la forma de onda transitoria para la ubicación de la falla que ocurre en el sistema de distribución [9].
Materiales y métodos
Se han propuesto varios métodos para la localización de fallas eléctricas, pero no son fácilmente aplicables a los sistemas de distribución. Esto se debe principalmente a líneas cortas y heterogéneas, ramales laterales, tomas de carga y un menor grado de instrumentación en los sistemas de distribución.
Actualmente, los principales métodos utilizados para la localización óptima de fallas monofásicas a tierra en las redes de distribución son el método de la impedancia, la inyección S, la onda viajera y los métodos de diagnóstico de puertos [10].
Además de todos los métodos mencionados anteriormente, el empleo de un localizador de fallas es la forma más práctica y asequible para los sistemas de distribución, proporcionando así la mejor localización probable de estas fallas [11]. El localizador de fallas es un sistema que no requiere infraestructuras sofisticadas, por lo que es un método adecuado para la mayoría de los sistemas de distribución. La asignación de un localizador de fallas a las redes podría restringir el área de identificación de falla por el centro de control supervisor, por lo que el tiempo requerido para la localización disminuiría sustancialmente. Esto lleva a mejorar el tiempo de restauración y los índices de confiabilidad del servicio eléctrico. Sin embargo, el uso de localizadores de fallas en todas las ubicaciones candidatas es innecesario y costoso, por lo que se necesita un análisis rentable para determinar óptimammente cuántos localizadores de fallas se requieren y dónde se deben ubicar para aprovecharlos al máximo [12].
La detección de fallas de alta impedancia (FAI) puede ser una función de protección en dispositivos electrónicos inteligentes en redes de distribución de energía [13]. FAI se puede definir como una falla que atrae corrientes bajas para que se disparen los dispositivos de protección convencionales, como los relés de sobrecorriente o los fusibles. Debido a la baja magnitud de la corriente de falla, la falla de alta impedancia no daña los componentes del sistema, pero es un peligro para la seguridad pública porque a menudo involucra un arco eléctrico que aumenta el riesgo de incendio [4].
A lo largo de los años, han surgido varios métodos para detectar fallas en un sistema de distribución. Mortazavi, et al. [14], presenta, un algoritmo para detectar fallas de alta impedancia mediante extracción de características basado en la transformada wavelet (TW) y una red neuronal. La extracción de las características más relevantes de la señal se obtiene de clasificar la transformada wavelet según su forma, por ejemplo, Haar, Symlet, Daubechies, Coiflet y Biorthogonal; para cada wavelet mencionada se realiza una descomposición de diferentes niveles, lo que permite el análisis para detectar una falla.
En las redes de distribución se generan diferentes tipos de fallas por cortocircuito, por lo que Guo, et al. [15] sugiere, utilizar el paquete de software CYME que permite la construcción de una red de distribución y la simulación de varias fallas por cortocircuito. Mediante Matlab - Simulink se puede descomponer y reconstruir señales en diferentes niveles utilizando la transformada wavelet, lo que permite mejorar la velocidad de detección de fallas.
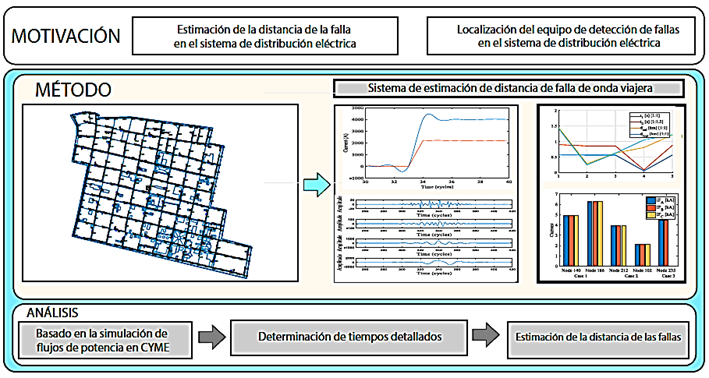
La Figura 1 representa la estructura de esta investigación. En esta Figura se muestra el escenario de diseño del sistema de la red de distribución y el análisis dinámico realizado ante la ocurrencia de una falla en uno o más nodos del sistema de estudio. Para este análisis es necesario obtener el perfil de cortocircuito y observar el proceso de la transformada wavelet, mismo que permite describir lo que sucede en el sistema para determinar las distancias de fallas y el nodo de origen cuando el sistema presenta una o varias. Los datos resultantes de este estudio permiten construir la métrica con la información crítica sobre la ubicación y comportamiento del sistema.
El análisis de estado transitorio requiere técnicas que exploten la relación entre los parámetros del sistema, la frecuencia transitoria y la velocidad de onda. Por esta razón, Magagula, et al. [16] sugiere utilizar la transformada wavelet, ya que las frecuencias altas tienen una mejor resolución en el tiempo.
Un componente de alta frecuencia se puede ubicar con menos error relativo que un componente de baja frecuencia. Por el contrario, las frecuencias bajas tienen una mejor resolución en el dominio de la frecuencia que los componentes de alta frecuencia [17]. Existen diversos métodos para la localización y cálculo de la distancia de falla en los sistemas eléctricos de potencia, entre ellos el método de la onda viajera, que se aplica en la mayoría de los casos para la localización de fallas en los sistemas de transmisión.
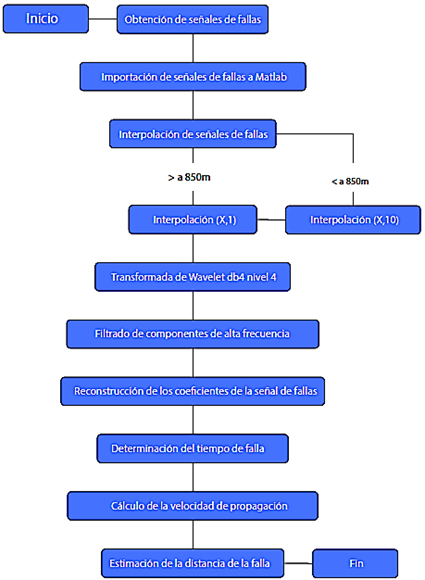
El diagrama de flujo se muestra en la Figura 2. Para obtener señales de fallas es necesario generar un perfil obtenido de CYME en análisis dinámico. Este perfil depende de los datos originales del sistema. Si esta información proporcionada no es correcta, es obligatorio interpolar; por lo tanto, el análisis de la transformada wavelet propone un filtro de Daubechies y de falla para determinar el tiempo y la velocidad de propagación, que es una posible estimación de la distancia de falla desde el reconectador más cercano.
En los sistemas de distribución se implementa el método de onda viajera, el cual tiene baja precisión cuando la configuración de las líneas cambia de impedancia, por lo que Li, et al. [18] propone, un método preciso de localización de fallas en la red de distribución basado en la onda viajera con múltiples puntos de medición. Para obtener múltiples puntos de medición en las redes de distribución [19], [20] utilizan relés digitales en las subestaciones, IED a lo largo de los alimentadores primarios, sensores SCADA en el circuito alimentador y medidores inteligentes en los clientes. Todos ellos tienen la propiedad de almacenar información sobre la operación de la red de distribución, obteniendo así múltiples puntos de medida.
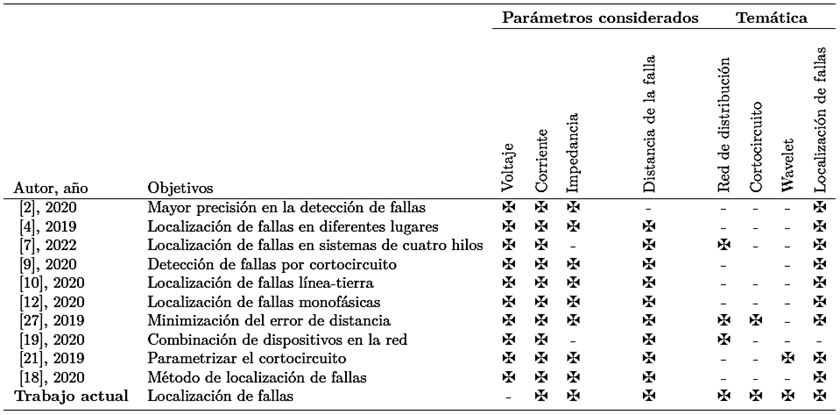
En la Tabla 1 se expone la nomenclatura, así como la descripción de abreviaturas que se están utilizando en esta investigación. Se propone la creación del estado del arte pues es una excelente herramienta para que el investigador pueda obtener información sobre el tema y desarrollar la estructura fundamental a través de la cual se expone el posible análisis y evaluación del modelo matemático, ver Tabla 2.
Existen diversos métodos para la localización y cálculo de la distancia de falla en los sistemas eléctricos de potencia, entre ellos el método de la onda viajera, que se aplica en la mayoría de los casos para la localización de fallas en los sistemas de transmisión. En los sistemas de distribución se implementa el método de onda viajera, el cual tiene baja precisión cuando la configuración de las líneas cambia de impedancia, por lo que en [18] se propone un método preciso de localización de fallas en la red de distribución basado en la onda viajera con múltiples puntos de medición.
Además, Myint y Wichakool [21] proponen, un algoritmo para la estimación de la distancia de falla en redes de distribución usando la onda viajera transitoria y la transformada wavelet, usando las señales de onda viajera actuales de la barra de la subestación con los primeros tiempos de llegada de la componente diferencial aérea y secuencias cero. Para calcular la distancia de falla estimada se puede desarrollar el análisis utilizando la Wavelet madre DB6 y nivel 1. Sin embargo, esto es posible solo cuando se trata de fallas simétricas [22].
En la actualidad, las herramientas computacionales de geoprocesamiento SIG se utilizan para diseñar una red de distribución eléctrica, obteniéndose una base de datos georreferenciada en la que se aplica el algoritmo de expansión mínima (MST). Este método representa una de las herramientas matemáticas utilizadas en problemas de simulación y optimización de las redes eléctricas [23], [24]. Una base de datos georreferenciada también permite aplicar algoritmos como K-Means y Elbow para una ubicación más precisa de los dispositivos de protección [25], [26].
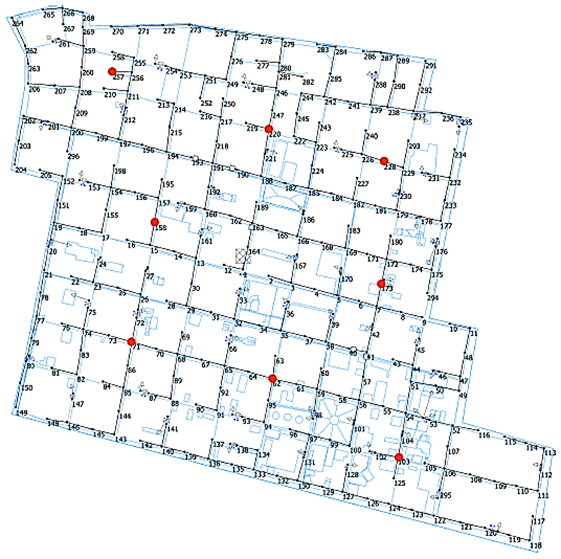
Como escenario de prueba y estudio se ha diseñado un sistema de red de distribución eléctrica con todos sus elementos. Esta red contiene reconectadores, subestaciones, cargas, entre otros. Con todos los datos establecidos en el diseño se asegura la correcta ejecución del flujo de potencia y se garantiza determinar el perfil de voltaje para el cliente. En la Figura 3 se puede observar una breve representación de la red de distribución eléctrica con detalles de la caída de voltaje, carga de reconectadores, carga de subestación, entre otros. Este sistema de diseño representa un caso de estudio para el análisis de fallas y permite una búsqueda prioritaria de la ubicación de nodos. Debido a que todo el sistema de estudio se encuentra geolocalizado, esto supone una estrategia de implementación mucho más realista.
Formulación del problema y metodología
Se presentan casos de estudio que contienen fallas en el sistema de distribución eléctrico que son identificadas por el método de la transformada wavelet. La adquisición de una base de datos que describa el funcionamiento del sistema en estado dinámico se realiza en el software CYME. Este software permite simular la estabilidad transitoria del sistema con sus respectivas características adquiridas por el método de identificación. Para esto, los datos deben contener como variable fundamental la información del comportamiento actual de la falla y esta debe ser interpolada si la distancia es menor a 850 metros, que es el umbral para tener un mejor muestreo de la señal.
El método de la onda viajera calcula la distancia de falla considerando un sistema sin cambio de impedancia homopolar positiva. Las redes de distribución están sujetas a fallas de diferente origen o naturaleza. Estas fallas afectan los componentes de la red eléctrica, generando perturbaciones en su correcto funcionamiento
y transitorios en las señales de corriente y voltaje. Por lo tanto, es necesario identificar cuando ocurre una falla usando la transformada wavelet.
La transformada wavelet es una herramienta efectiva para la identificación de fallas debido a su funcionalidad para procesar y analizar señales transitorias. La TW se puede utilizar para obtener información simultánea sobre el tiempo y la frecuencia de una señal [14].
El sistema de distribución eléctrico contiene transformadores trifásicos en media tensión con potencia que varían entre 30 kVA y 200 kVA. La configuración de los conductores está propuesta con calibres 1/0 para las fases y 2 tipo ACSR para el conductor neutro.
Para una línea aérea, la ubicación de los reconectadores depende de las características del sistema, pero para esta investigación se utilizaron los indicadores de falla para definir estas ubicaciones. Otro parámetro importante es la capacidad de los conductores, esto asegura su cambiabilidad.
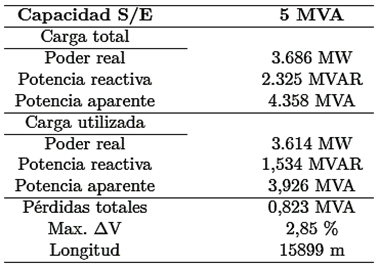
Todos los escenarios se encuentran geolocalizados con las condiciones óptimas para ejecutar un flujo de potencia, ver Figura 4. Los resultados encontrados se muestran en la Tabla 3 donde se pueden observar los parámetros más relevantes para cada caso de estudio.
El análisis de señales mediante la transformada wavelet se basa en la dilatación y traducción de una ondícula madre en la señal. La operación de escalado dilata y comprime la ondícula madre, lo que da como resultado señales de baja y alta frecuencia, respectivamente [14].
(1)
(2)
Donde:
• s - Scala.
• μ - Traducción de la función wavelet en el dominio
de la señal de análisis.
• t - Tiempo.
Diferentes wavelets madre están asociadas con la familia: Daubechies, Coiflets y Symmlet. Para los estudios de los casos presentados en esta investigación se utiliza el nivel 4 [dB4] de la wavelet de Daubechies.
Se propone localizar la falla utilizando el método de la onda viajera, el cual calcula la propagación de la onda y depende de los parámetros inductivos y capacitivos de la ecuación (3) obtenidos a partir de la impedancia de secuencia cero y de secuencia positiva.
(3)
L representa la inductancia de la línea de distribución por unidad de longitud. En contraste, C representa la capacitancia de la línea de distribución por unidad de longitud. Para cualquier caso, los parámetros pueden expresarse en kilómetros o metros; por lo tanto, la velocidad calculada se describirá en km/s o m/s. Las configuraciones de las líneas de distribución afectan la forma en que las ondas viajeras viajan a través de la red (Tabla 4).
Para calcular la distancia de falla, además de la velocidad de la señal, es necesario determinar el tiempo de la señal utilizando la longitud de onda y su frecuencia de muestreo, que es igual a 3.3 kHz.
(4)
(5)
En la ubicación del equipo de detección de fallas llamado LF, se implementa el método del codo de Jambú para estimar la cantidad de clústeres necesarios. El algoritmo k-means permite un mejor agrupamiento de los indicadores de falla dentro de la red de distribución presentada en el caso de estudio (Tabla 5).
Para probar la efectividad del algoritmo propuesto, se diseña una red de distribución de 22 kV georreferenciada con QGIS, ver Tabla 1. Estas coordenadas se importan a Matlab para conformar el grafo en el que se aplica el árbol de mínima expansión partiendo de un vértice raíz y encontrando todos sus nodos enlazados. Este análisis se realiza con base en las relaciones que permiten conectar los nodos, siendo el peso considerado la menor distancia [28]. Un árbol de expansión de peso mínimo es un dígrafo de borde ponderado conectado a todos los vértices sin la presencia de bucles [29], [30].
El alimentador propuesto cuenta con 295 nodos, 48 transformadores trifásicos de dos devanados cuyas potencias en kVA son 30, 50, 75, 112.5, 150 y 200, un transformador monofásico de 75 kVA, 54 cargas concentradas y cinco reconectadores trifásicos, dando como resultado un alimentador de 5 MVA de carga instalada; ver Figura 4. En la Tabla 3 se muestran los datos generales y en la Tabla 6 los casos de estudio propuestos.
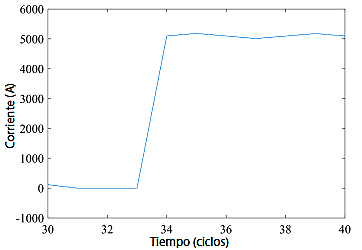
Según el caso de estudio expuesto, el punto de partida es una falla por cortocircuito trifásico en el nodo 140, a 1427 metros de la subestación de media tensión. Los datos del cortocircuito se obtienen del almacenamiento de eventos que contiene el dispositivo de protección y conmutación, que es el reconectador 41-57 con una frecuencia de muestreo de 3,3 kHz. A partir de los datos registrados se origina la forma de onda de operación del sistema de distribución en falla, ver Figura 5.
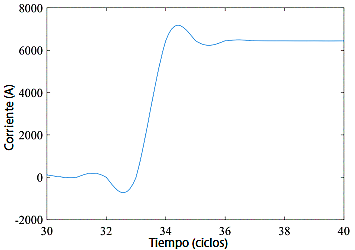
Partiendo del mismo caso de estudio, se presenta una falla trifásica con cortocircuito cercano a la subestación a una distancia de 274.6 metros. La señal de falla se obtiene del almacenamiento de eventos por parte del dispositivo de protección y conmutación, el reconectador 163-164. Como la falla es inferior al umbral, se procede a interpolar para un mejor muestreo; ver Figura 6.
Como segundo caso se presenta un cortocircuito trifásico simultáneo. Por tanto, se tienen dos distancias, una para cada cortocircuito. La primera distancia es de 625.8 metros, inferior al umbral por lo que requiere una interpolación. La segunda distancia es de 1051.7 metros, tomada desde la subestación eléctrica. Las señales se obtienen de los reconectadores 41-57 y 191-193; ver Figura 7.
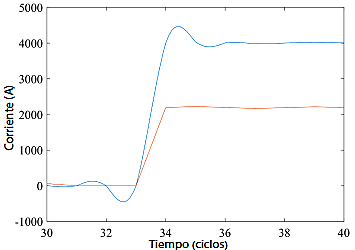
Figura 7 Cortocircuito trifásico simultáneo en dos nodos del sistema de distribución eléctrico (CYME).
Ocurre una falla bifásica dentro de la zona del reconectador 190-191 a 1219 metros de la subestación. En este caso, las corrientes de falla son simétricas porque no hay cambio de impedancia en las líneas de distribución, ver Figura 8.
Resultados y discusión
Se utiliza una transformada wavelet de la familia Db4 y orden 4 a partir de las señales de fallas obtenidas de cada caso. La señal se reconstruye usando el nivel máximo basado en la estructura de descomposición de la wavelet.
Los detalles de las señales para todos los casos son similares con la variación en su amplitud debido al número de coeficientes calculados. Una de las variables esenciales para aplicar el método de la onda viajera y la posterior localización de la falla es el tiempo exacto (td). Este tiempo resulta de la diferencia entre los dos picos (valor RMS) consecutivos en el instante de la falla, el cual se calcula para cada uno de los casos.
Para la aplicación del algoritmo de localización e identificación de fallas es necesario determinar el tiempo (td) para cada caso de estudio. Este tiempo será similar para cada tipo de falla y se puede obtener de la señal presentada en la Figura 9, la cual corresponde al análisis de la identificación de la falla distante de la subestación que fue ubicada en el nodo 140.
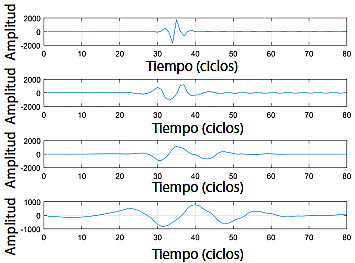
Figura 9 Detalle de la señal de wavelet para calcular el tiempo de fallas lejos de la subestación. Amplitud enamperios vs. TW del orden 4
Ahora bien, para la falla que ocurre en el nodo 186 ubicado cerca de la subestación, la información de la base de datos obtenida por el reconectador es interpolada debido a la poca cantidad de datos. Esto permite una mejor señal a analizar para la identificación de fallas y determinación del tiempo td, Figura 10.
Se analiza la ocurrencia de dos fallas simultáneas, una ubicada en el nodo 212 y la segunda en el nodo 102, donde estas pertenecen a las zonas de los reconectadores 41-57 y 191-193 respectivamente. De estas fallas se obtuvieron dos bases de datos diferentes en las que se realizó un análisis independiente para cada señal con el objetivo de identificar dónde ocurrió la falla y de determinar los tiempos td de cada señal de falla. Estos resultados se presentan en las Figuras 11 y 12.
La Figura 13 muestra el detalle de la señal de wavelet con la cual se obtiene el tiempo td para calcular la distancia en el caso de la falla bifásica que ocurre en la zona del reconectador 190-191.
Una vez identificada la ocurrencia de la falla y la distancia estimada desde su origen, se implementa el método del codo de Jambú para determinar el número requerido de localizadores de fallas a instalar en la red de distribución de estudio. El resultado del método del codo de Jambú se presenta en la Figura 14.
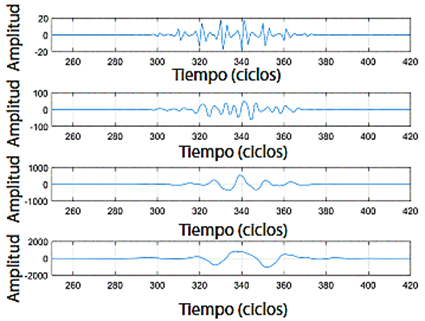
Figura 10 Detalle de la señal de wavelet para calcular el tiempo de fallas cercanas a la subestación. Amplitud en amperios vs. TW del orden 4
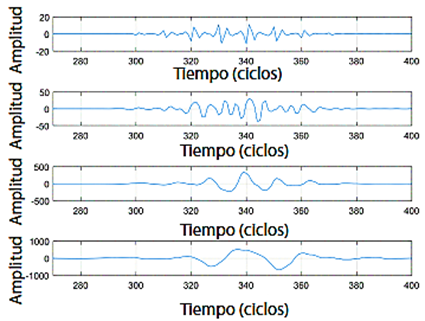
Figura 11 Detalle de la señal de wavelet para el cálculo del tiempo de falla 1. Amplitud en amperios vs. TW del orden 4.

Figura 12 Detalle de la señal de wavelet para el cálculo del tiempo de falla 2. Amplitud en amperios vs. TW del orden 4.
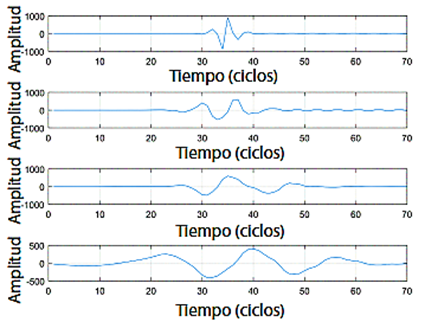
Figura 13 Detalle de la señal de wavelet para el cálculo del tiempo para el cortocircuito bifásico. Amplitud en amperios vs. TW del orden 4
El método k-means permite obtener la ubicación óptima donde se debe instalar cada localizador de falla. La Figura 5 muestra la ubicación óptima de los 8 localizadores de falla, representados por puntos rojos.
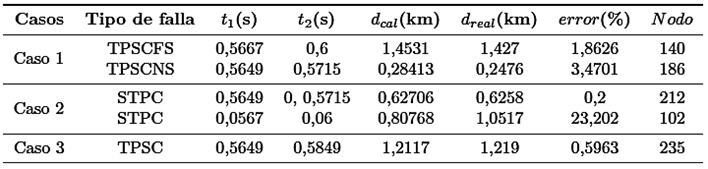
Para comprobar que el algoritmo desarrollado estima correctamente la distancia de la falla, se presenta la Tabla 7 , la cual indica los resultados obtenidos en las pruebas para cada caso. De estos resultados, se puede evidenciar que los valores de distancia de falla calculados en comparación con las distancias reales de fallas presentan un margen de error inferior al 30 %, por lo tanto, se pueden considerar satisfactorios.
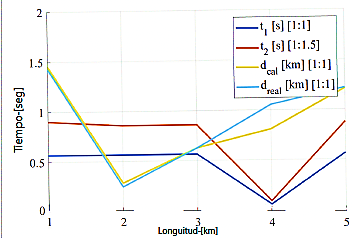
El cálculo de la distancia depende directamente del tiempo exacto de la falla. En la Figura 15 se muestra como la curva de distancia calculada también varía ante cambios en las curvas de los tiempos t1 y t2. En esta misma Figura se ve que la curva de distancia calculada es similar a la curva de distancia real, resultado que valida la factibilidad del método.
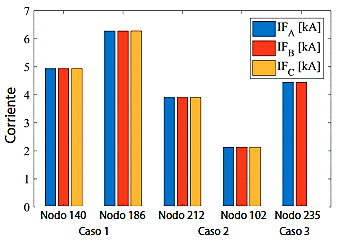
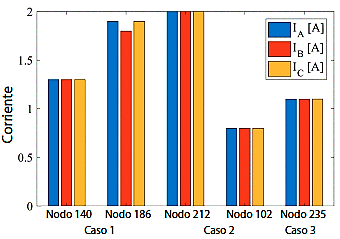
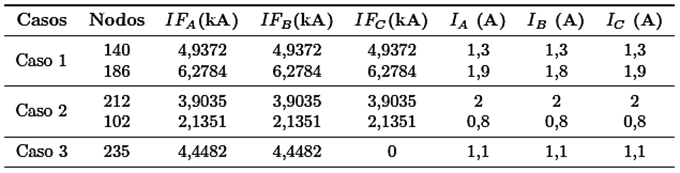
En la Tabla 9 se muestran la corriente nominal y la corriente de cortocircuito para cada nodo donde ocurre la falla. La Figura 14 muestra la corriente de falla para cada nodo, mientras que la corriente nominal para cada nodo se muestra en la Figura 17.
En la Figura 16 se puede evidenciar que el nodo 212, que se encuentra distante de la subestación, presenta la máxima corriente nominal del sistema porque tiene una mayor cantidad de carga conectada. Por el contrario, el nodo 102 posee la corriente nominal más pequeña dentro del sistema de estudio debido a que este nodo tiene conectada una pequeña carga. En el caso de la Figura 15, se observa que la máxima corriente de falla se presenta en el nodo 186 cercano a la subestación y con una gran cantidad de carga conectada, mientras que el nodo 102 nuevamente se presenta la mínima corriente de falla por la misma razón de tener una carga menor conectada.
Los voltajes en los nodos del sistema de distribución eléctrica varían dependiendo de la distancia a la que se encuentran ubicados estos nodos con respecto a la subestación eléctrica. A mayor distancia de la subestación mayor es la caída de voltaje en ese recorrido. La Tabla 8 muestra los valores del voltaje nominal y del voltaje de falla para cada caso de estudio.
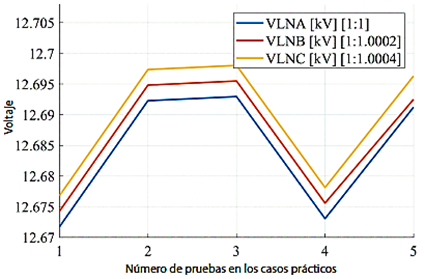
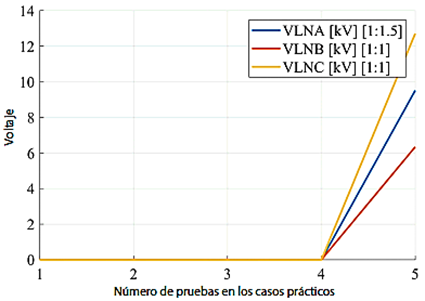
En la Figura 18 se analizan los valores de voltaje para cada fase en kV. De esta Figura se puede evidenciar cómo los voltajes en cada nodo varían en función de la distancia a la que estos nodos se encuentran con respecto a la subestación. La Figura 19 muestra cómo el voltaje de falla de cada fase varía según las características de la falla (Tabla 9).
Discusión
El rendimiento del algoritmo de localización de fallas basado en la transformada wavelet y la velocidad de propagación de la onda viajera dependen de la configuración de las líneas del sistema de distribución y la ubicación de la falla. Cuando el diseño de las líneas no presenta cambio de impedancia, el algoritmo muestra un excelente desempeño en el cálculo de la distancia de falla, por lo que la ubicación del punto de falla es más precisa. Cuando la configuración de las líneas presenta cambios de impedancia es necesario que el alimentador cuente con IED y equipos de protección instalados en múltiples nodos para tener más información sobre la ocurrencia de las fallas, lo que permite que el algoritmo presente un mayor rendimiento.
Se realizaron varias simulaciones con ocurrencias de fallas lejos y cerca de la subestación. Las fallas que ocurrieron a distancias mayores a 850 m no requieren interpolación de los datos, mientras que las fallas cercanas a la subestación deberán interpolarse. Ante esta hipótesis se determinó que el umbral de interpolación es de 850 m.
Es necesario realizar un análisis preciso de la ubicación de la falla, porque en la red de distribución pueden existir distancias iguales basadas en los equipos de protección y maniobra, como los reconectadores. Esto permite la zonificación y reduce el margen de error en la localización de las fallas. Sin embargo, incluso con el análisis por zona de reenganche, todavía pueden existir distancias iguales hasta el punto de la falla. Por lo tanto, se propone la ubicación de un dispositivo localizador de falla (LF) para lograr una ubicación precisa de la falla. Esto permitirá visualizar de manera clara qué sección de la línea de distribución está afectada por la falla.
Conclusiones
La localización de fallas en los sistemas de distribución eléctrica es fundamental para mejorar su confiabilidad y reducir el tiempo de interrupción del servicio eléctrico; en este artículo se relaciona la transformada Wavelet con la onda viajera para proponer un método de localización de fallas.
La caracterización del sistema de distribución muestra que la variación de los parámetros de las líneas influye en el cálculo de la velocidad de la onda viajera a los diferentes equipos de protección instalados en el alimentador, cuya frecuencia de muestreo varía según la marca y modelo.
Para calcular la distancia de la falla de manera precisa, es crucial seleccionar adecuadamente la función madre de la transformada wavelet. Esta elección nos permitirá identificar de manera óptima los dos picos máximos posteriores a la falla, lo que nos dará una estimación aproximada de la distancia. Es importante tener en cuenta que esta aproximación puede tener un margen de error permisible de hasta un 30 %.
La señal de falla capturada por los dispositivos de protección de la red puede provenir tanto de equipos cercanos como lejanos a la subestación. En caso de que los datos disponibles para construir la señal de falla sean limitados y no permitan obtener una señal suavizada, es necesario realizar una interpolación para ampliar la base de datos y obtener una aproximación más precisa de la falla. En el marco de este estudio, se han llevado a cabo pruebas que demuestran que la distancia óptima es de 850 metros.
La metodología implementada en este estudio de caso ha permitido la localización precisa de fallas en el sistema de distribución mediante el análisis de las señales de corriente de cortocircuito registradas por los reconectadores cercanos a la ubicación de la falla. Es crucial identificar correctamente los coeficientes de detalle, ya que estos coeficientes tienen un impacto directo en el cálculo de la distancia de la falla. Además, es importante tener en cuenta que la duración de la falla también influye en este cálculo. Es importante destacar que la metodología propuesta es aplicable únicamente en escenarios donde no se produzcan cambios significativos de impedancia en las líneas de distribución.
Para la cuantificación de los equipos detectores de fallas, se empleó el método del codo de Jambú. Este método se utiliza para implementar el algoritmo de k-means, el cual permite ubicar los equipos detectores de fallas en nodos estratégicos.