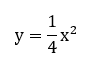Introducción
Actualmente, las Tecnologías de la Información y Comunicación (TIC) se han convertido en el medio para transmitir los conocimientos, por ello es importante promover entre la comunidad docente el uso del software educativo, como herramienta en el aprendizaje de sus áreas de conocimiento, que puede cuantificarse en un mejor aprovechamiento de sus estudiantes.
Para el constructivismo, el estudiante toma un papel dinámico, ellos deben “hacer”, en la comprensión y sentido de una “información”, no son sujetos pasivos que “esperan” el aprendizaje. Ahora bien, la información que deben comprender y dar sentido, ¿quién la proporciona?, ¿cómo la proporciona?, las respuestas a estas preguntas son variadas y han dado pie a diferentes perspectivas del constructivismo. Las diferentes perspectivas están fundamentadas en las investigaciones de Piaget, Vygotsky, Brunner, entre otros. Woolfolk extrae de Palincsar y Phillips una forma de organizar las perspectivas constructivistas es refiriéndose a dos formas de constructivismo: la construcción psicológica y la social (Woolfolk, 2014).
Según Vigotsky, cada estudiante es capaz de aprender muchas cosas en su nivel de desarrollo, pero existen otras que se encuentran fuera de su alcance pero que pueden ser aprendidos con ayuda de una o varias personas que se encuentren aventajadas. La distancia entre lo que el estudiante puede aprender por sí mismo y lo que puede aprender con ayuda, es lo que se denomina “zona de desarrollo próximo”. Vigotsky atribuye al docente un papel esencial, considerándolo facilitador en la construcción de las estructuras mentales y así construir aprendizajes complejos (De la Torre Zermeño, 2005).
En la siguiente Figura 1 podemos distinguir la zona de desarrollo próximo.
Otro icono del constructivismo social es Jerome S. Bruner (Bustos Cobos, 2002), quien resalta el papel de la actividad como parte esencial de todo proceso de aprendizaje. “Así pues, el desarrollo de la mente es, por fuerza, un desarrollo asistido siempre desde fuera (...). Y es que los límites del desarrollo dependen de cómo una cultura ayuda al individuo a servirse del potencial intelectual del que está dotado”, acota. Podemos observar que Bruner coincide de la influencia externa en el desarrollo cognitivo, de la influencia de la sociedad donde se encuentre y esta influye hasta dónde puede llegar otorgando los andamios al individuo.
A su vez, el autor aporta a la teoría constructivista, añadiendo a la postura de Vigotsky de la actividad guiada o mediada, la necesidad de adquirir información a través del contacto directo, teniendo una experiencia personal, es así donde surge el llamado aprendizaje por descubrimiento en el que el estudiante es el eje central del proceso de aprendizaje. Para Bruner no solo la interacción entre el estudiante y el profesor va a permitir que esta experiencia tenga algún sentido, el acto pedagógico no sería tanto una transmisión como más bien una transacción entre la cultura del educando y la del docente. El adulto, depositario de una cultura, a través de los intercambios con el niño, hace posible que este último construya sus conocimientos (Giry, 1989).
Las experiencias personales se dan de diferentes maneras, las cuales iremos describiendo en las siguientes líneas y representa la metodología que se pretende comprobar en este trabajo.
1.1 Aprendizaje por experiencia directa
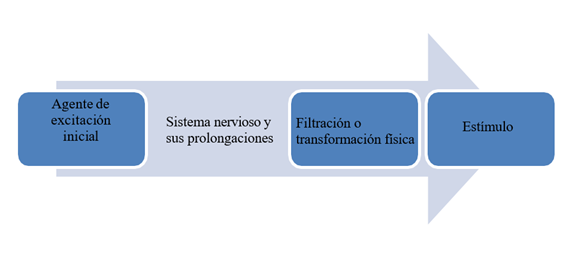
El conocimiento desde la experiencia personal, con el contacto directo del objeto de estudio es llamado por Bruner como experiencia directa. A decir del propio Bruner “La Experiencia Directa”, la expresión es algo inexacta, en la medida de que todo conocimiento se capta o percibe previa una actividad, y el conocimiento que se adquiere de esa actividad está ligado íntimamente con ella. Para poder concebir abstractamente el concepto experiencia, es necesario realizar un análisis del antiguo significado de “estímulo”, para después compararlo con lo que, a razón de Bruner, es la verdadera relación del individuo y la especie.
El antiguo significado de estímulo corresponde a “el resultado de una especie de filtración o de transformaciones físicas, a través del sistema nervioso y de sus prolongaciones, del agente de excitación inicial” (Bruner & Olson, 1973), como veremos en la siguiente Figura 2:
El crecimiento cognoscitivo, según Bruner, es un proceso integrado de actividades, donde el individuo aumenta el dominio sobre su medio ambiente. El conocimiento es construido por el individuo, es él quien lo adquiere, y almacena.
1.2 Aprendizaje por experiencia mediatizada
Bruner, nos habla de otras maneras de adquirir el aprendizaje, sin que deba existir una experiencia directa con el objeto de estudio. Estas maneras serán descritas a continuación.
Una de las maneras de obtener un conocimiento es “extraer experiencias por medio de personas interpuestas” (Bruner & Olson, 1973). El individuo no entra en contacto directo con el medio, sino con la experiencia de otra persona.
La otra posibilidad de aprendizaje es por medio de información codificada, esta es trasmitida a través de un tercer medio, mismo que pude ser por palabras orales o escritas, por largometrajes o películas, diagramas y todo medio visual o auditivo. Este medio de enseñanza reemplaza de alguna manera la experiencia directa en la enseñanza tradicional. Bruner propone tres modos de experiencias para obtener el conocimiento: Experiencia directa, experiencia mediatizada a través de personas interpuestas y experiencia mediatizada a través de un tercer medio (Bruner & Olson, 1973).
2. Teoría del crecimiento cognoscitivo según Bruner
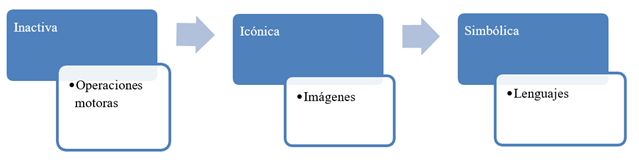
El sujeto codifica los datos que le llegan del exterior reduciéndolos a categorías de las que dispone para comprender el entorno, el comportamiento no es pues algo que depende únicamente y mecánicamente de un estímulo objetivo externo; el sujeto transforma la información que le llega por medio de tres sistemas de representación: la representación activa, icónica y simbólica (Aramburu Oyarbide, 2004). Veamos detalladamente cada sistema de representación:
La representación activa se puede entender como aquella en la que es necesaria una serie de etapas, un conjunto de acciones u operaciones motoras con la finalidad cierta y certera de alcanzar un resultado que motiva dichas acciones. De esta forma se realizan respuestas motoras para manipular el medio en el que se encuentra. “Consiste en representar cosas mediante la reacción inmediata de la persona” (Schunk & Purdue, 1997), es decir actuamos con reflejos activos para alcanzar nuestro propósito, sin proponernos una metodología.
Mientras que la representación icónica tiene un grado más de evolución, se vale de la imaginación, las imágenes y los esquemas más o menos complejos, para hacer una representación no material de su entorno, para ello Bruner señala que es necesario contar con un mínimo nivel determinado de destreza y de prácticas motrices para poder desarrollar la imagen deseada (Aramburu Oyarbide, 2004).
Estas últimas siempre son inanimadas, pues los objetos se transforman mentalmente y se reflexionan sus funciones sin atender a su función o utilidad (Posada, 1993). Dado que no es posible definirlos cabalmente, pero para escoger la imagen a representar abstractamente no se siguen criterios arbitrarios.
En cuanto la representación simbólica sube una escala más de la acción y la imaginación; dado que se basa, para la representación del entorno, de símbolos por medio de los cuales se puede presuponer objetos nunca vistos (Aramburu Oyarbide, 2004). De igual forma se representan conocimientos con características tradicionales, de manera arbitral; una ventaja intrínseca en este tipo de representación, es que permite transformar y representar el conocimiento con una gran elasticidad que con los otros dos tipos (Posada, 1993). Además de ello, contiene una serie de estipulaciones lógicas, que derivan de un sistema teórico regido por una serie de reglas, mismas que hacen transformar las estipulaciones.
En la siguiente Figura 3 se sintetizan las diferentes formas de representación, desde la activa, icónica y simbólica.
La importancia de incorporar la computación en las matemáticas, radica en la potencia del software de visualizar dinámicas de conceptos, muchos de ellos abstractos, haciendo posible que el estudiante explore y manipule diversos casos que, en el pizarrón, rotafolio o retroproyector no es posible (Villagrán et al., 2018).
Por otro lado, la Geometría Analítica (Guerra, 2004) posee lenguaje propio y una estructura conceptual compleja en su contenido por lo que genera dificultades en su enseñanza y su aprendizaje (Segura Vidal et al., 2017). Diversos estudios han demostrado que al manipular un programa y tener la representación algebraica, ver sus cambios, estudiantes razonan, plantean y argumentan sus hipótesis para comunicarlas de forma escrita y verbal con sus compañeros y docente (Pizarro Carrillo & Ramírez Lobo, 2017).
Después de un análisis de las diversas herramientas educativas para la enseñanza de la Geometría Analítica (Swokowski, 1996), elegimos el software educativo denominado: Wiris Cas, generando la hipótesis que, al incluir un Sistema de Geometría Dinámico, creemos que permite al estudiante transitar por los tres sistemas de representación que propone Bruner: activa, icónica y simbólica. Por lo tanto, el objetivo de este trabajo es demostrar si el uso del software Wiris en el aprendizaje de la parábola conduce los tres sistemas de representación que propone Bruner.
Metodología
La metodología utilizada fue la observación científica controlada, puesto que “el investigador prepara el campo de estudio, fija su atención en ciertos puntos de interés del fenómeno observado y aplica instrumentos de precisión para medir la calidad de los datos” (Pérez et al., 2020). La observación de acuerdo a la participación del investigador en el fenómeno observado es científica de participantes, donde este se integra al grupo de estudio y lo examina por dentro y por fuera; por dentro, participando, como un elemento más del grupo y por fuera, captando todo lo que el sujeto o sujetos quieren decir o dejar de ver.
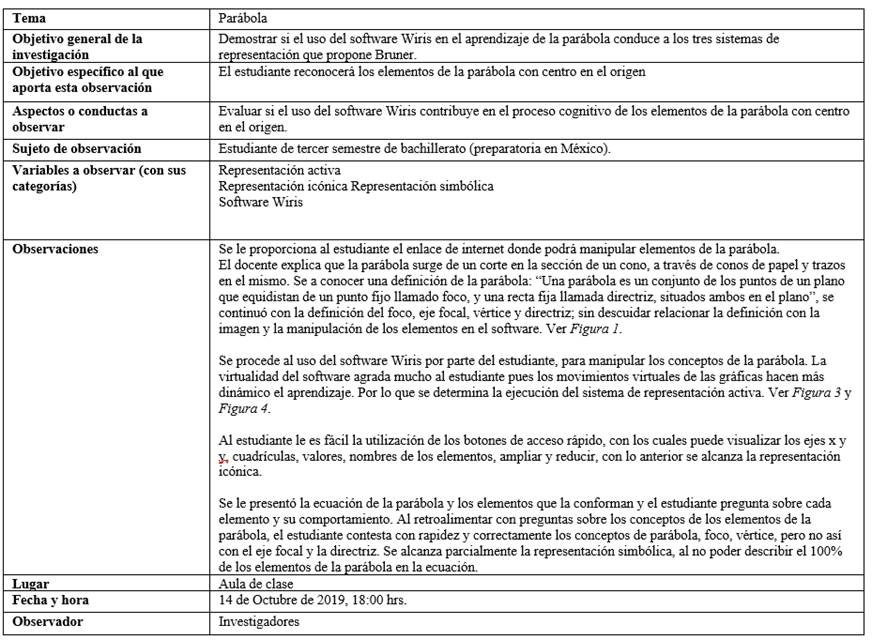
El sujeto de estudio es un estudiante de tercer semestre de bachillerato (preparatoria en México).
El instrumento empleado para el proceso de recogida de información (Tabla 1) y datos es una guía de observación, ya que observar no solo es “ir y mirar”, sino el considerar diversos puntos (Pérez et al., 2012).
Wiris CAS es una plataforma para cálculos matemáticos específicamente diseñada para la enseñanza de las matemáticas desde la primaria hasta la universidad, desarrollada por Maths for More dentro del programa Innova de la UPC (Platea, s.f). WIRIS CAS es una plataforma para cálculos matemáticos centrada en la usabilidad, se trata de un sistema de cálculo simbólico (CAS, en sus siglas en inglés) que incluye un sistema de geometría dinámica (DGS, en sus siglas en ingles), los usuarios acceden a una página web, donde pueden solicitar cálculos y recibir respuesta de modo inmediato. La versión de escritorio requiere licencia, sin embargo existe una versión gratuita del software a través del portal web: http://www.wiris.net/demo/wiris/es/cas.html.
La manera de uso es a través de un explorador de Internet, donde el usuario accede a una página y plantea ciertos cálculos, para recibir respuestas de ellos de manera casi inmediata. En una página HTML convencional, el motor matemático reside en el servidor de las diferentes instituciones que lo ponen al servicio de la educación y no en el ordenador del usuario. Las peticiones de cálculo se realizan vía el protocolo HTTP- POST y CGI. Esto consiste en ejecutar un programa que se comunica con la componente del motor Java y solicita cálculos y espera los resultados, que a la vez vuelve al cliente, es por ello que requiere de un ordenador para el usuario con navegador que admita Java 1.1 o superior (por ejemplo, Internet Explorer) (Sanz, s.f). Esta calculadora, igualmente permite representar gráficas de funciones, para comprobar propiedades de forma interactiva. Todas las propiedades anteriores lo hacen haciéndolo idóneo para nuestro caso de estudio, puesto que permite diferentes tipos de usos en el aprendizaje.
La interfaz de la versión gratuita en la Web del Software Wiris se aprecia en la Figura 4, en ella se puede observar en la barra de direcciones la URL de acceso gratuito y en la barra de menús las diversas áreas que abarca, cada una con una barra de herramientas.
Resultados
De acuerdo a una planeación previa, se ejecutaron 2 sesiones de formación, cada una con los siguientes temas:
• Elementos de la parábola.
• Construcción de parábolas con eje focal en x, a partir del foco y la directriz y su respectiva ecuación.
Las guías de observación de las tres sesiones se presentan a continuación en la Tabla 2:
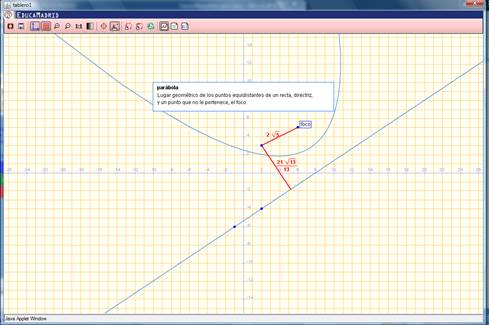
En la siguiente Figura 5 se muestra que esta fue manipulada en cada punto en color azul, para que las propiedades de la parábola se ajusten cada vez que esto suceda, como se observa en las Figuras 6 y Figura
7.
La segunda guía de observación se puede ver en la siguiente Tabla 3.
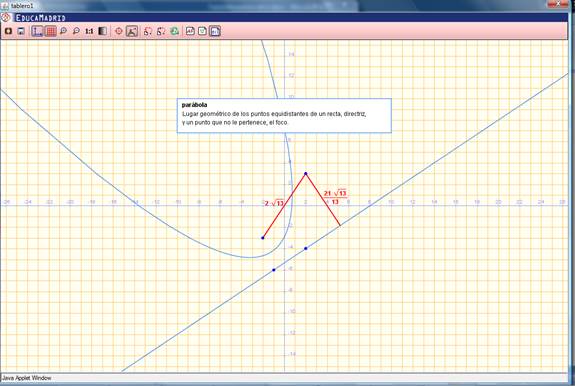
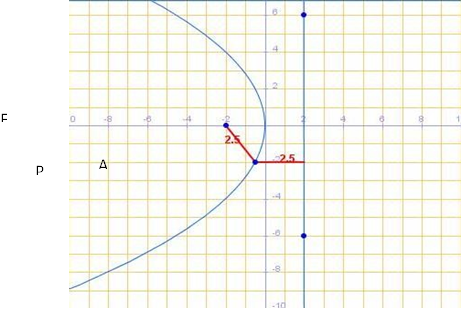
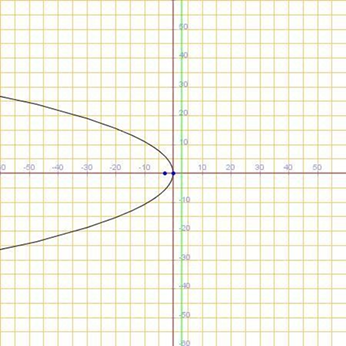
La parábola empleada para la recuperación de conocimientos previos, con foco en el eje de las x, para introducir el nuevo tema: coordenadas son F(p,0); la ecuación de la directriz l es por tanto 𝑥 = −p, donde p=-2, como se muestra en la Figura 8.
El ejemplo empleado con el estudiante para desarrollar una parábola con foco en el eje de las x es el siguiente:
Aplicando de nuevo la fórmula de la distancia entre dos puntos, deducir:
Se elevan ambos miembros al cuadrado y se simplifica:
Despejando y, obtenemos una ecuación equivalente de la parábola (Carpinteyro, 2018).
La ecuación de la parábola es una ecuación de segundo grado, al extraer la raíz
Si p>0, no deben tomarse en cuenta los valores negativos de x, por lo que la parábola se abre a la derecha del eje x, entonces, la parábola se abre a la derecha del eje y y se extiende indefinidamente hacia arriba y hacia abajo del eje x. Por lo tanto, la ecuación de la parábola es 𝑦2 = 4𝑝𝑥; las coordenadas de su foco son F(p,0) y la ecuación de su directriz es 𝑥 = −𝑝
Para ilustrar el cambio de signo en el foco, la ecuación de la parábola empleada es la siguiente: 𝑦2 − 12𝑥 = 0, donde
𝑝 = 3 y la ecuación de la directriz 𝑥 = −3
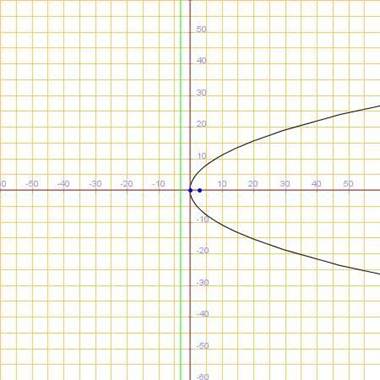
Si p<0, no deben tomarse en cuenta los valores positivos de x; por lo que, la parábola se abre a la izquierda del eje y se extiende indefinidamente hacia arriba y hacia abajo del eje x. Por lo tanto, la ecuación de la parábola es 𝑦2 = 4𝑝𝑥; las coordenadas de su foco son F(p,0) y la ecuación de su directriz es 𝑥 = −𝑝
La ecuación de la parábola ilustrada es la siguiente: −𝑦2 − 12𝑥 = 0, donde
𝑝 = −3 y la ecuación de la directriz 𝑥 = 3
Los resultados nos arrogan que las etapas del desarrollo cognoscitivo propuestas por Bruner, en la presente estrategia de aprendizaje de la parábola se desenvuelve de manera satisfactoria.
Discutamos cómo se logra cubrir cada etapa del desarrollo:
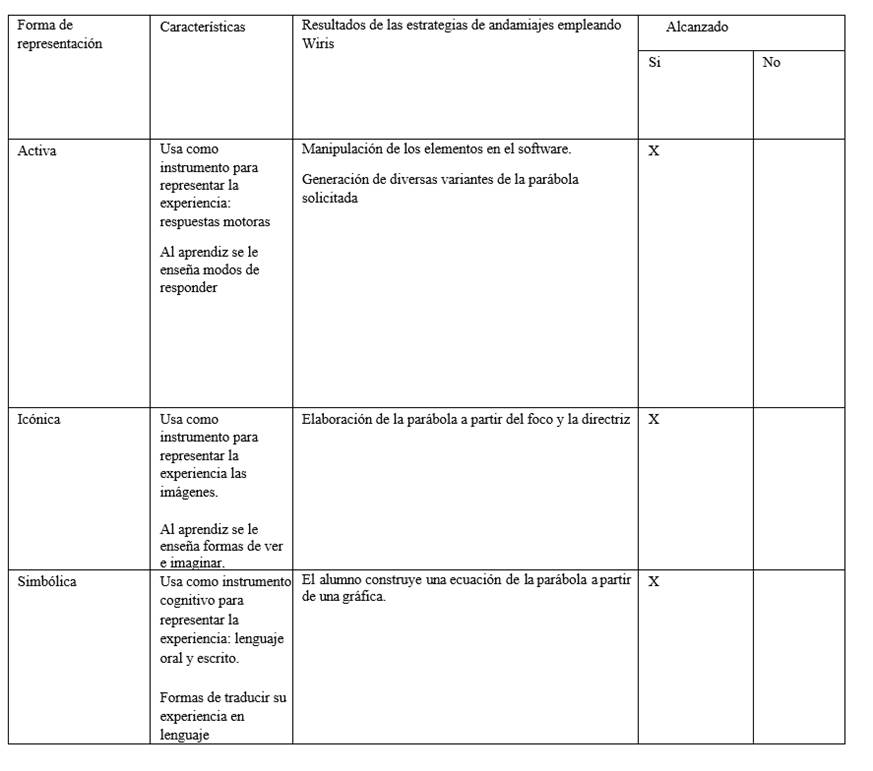
La etapa activa se presenta gracias a la interactividad que posee el software educativo denominado “Wiris”, en donde se respetan las propiedades que poseen las parábolas a medida que se va manipulando distintos elementos, mismos que fueron parte del objeto de nuestro estudio. Al respetarse las propiedades observamos de manera activa la definición de los elementos de la parábola, pudiendo citar como ejemplo la directriz que al moverse siempre conservaba la misma distancia del vértice que el vértice del foco, siendo estas últimas palabras la definición de la directriz. Gracias a la propiedad mencionada el estudiante pasa por la primera fase del desarrollo, de una manera exitosa y motivante para el estudiante.
La etapa icónica se desarrolla al graficar la parábola a través de los elementos de la misma y su graficación en el software, de esta manera ubica los elementos de la parábola y su representación. El software promueve el interés del estudiante al realizar variaciones en los datos y dinámicamente se reflejen los cambios en la gráfica, siendo relevante que el estudiante llegue hasta otros temas fuera del alcance de este libro. De cualquier manera, se respondieron a sus dudas, destacando el papel primordial del software, y rebasando las expectativas incluso del investigador.
La etapa simbólica se alcanza cuando al estudiante logra definir y elaborar ecuaciones de la parábola, obteniendo los valores de los elementos y así la graficación total de la misma. Siendo recomendable el software Wiris al obtener los valores de la ecuación de la parábola, a su vez graficar la parábola correspondiente, dando pie al “usuario” de alcanzar la etapa simbólica.
A través de la Tabla 4, se verifica si las formas de representación fueron alcanzadas.
Con lo anteriormente expuesto, resulta positiva la hipótesis planteada:
El software educativo influye completamente en el desarrollo cognoscitivo de la parábola según la teoría de Bruner.
El desarrollo cognoscitivo de Bruner, con el uso de la tecnología, otorga una gran confianza para seguir el curso del uso del software educativo Wiris, para el aprendizaje de la parábola.
El desarrollo de la presente labor culmina de una forma positiva pues como se ha venido señalando, la implementación del software educativo Wiris, es de gran utilidad para acabar con los prejuicios que existen en torno al proceso enseñanza-aprendizaje de un sector de las matemáticas, tal como lo es la parábola.
Según la teoría constructivista de Bruner, da mucha importancia a que el estudiante descubra el conocimiento, sin embargo, observamos que es necesaria la propuesta consiste en el software educativo sea una vía para el desarrollo cognoscitivo de la parábola en la materia de Geometría Analítica.
Conclusiones
Las Tecnologías de la Información y Comunicación están demostrando que son aliadas para la mejora de los procesos de enseñanza-aprendizaje, por lo tanto, resulta necesario fomentar en los docentes incursionar de una manera más vertiginosa en el ámbito de la tecnología educativa.
La teoría del crecimiento cognoscitivo según Bruner, permite fundamentar el empleo de las tecnologías en la enseñanza de las matemáticas.
Al realizar la fundamentación teórica del presente trabajo, se pudo percibir que se requiere hacer mayor número de investigaciones en este ámbito de la educación, para demostrar que las bases pedagógicas proporcionan un soporte al empleo de tecnologías aplicadas a la educación, así se les otorga la certeza a los docentes a poner en práctica lo investigado con la confianza de obtener buenos resultados de una manera eficaz y eficiente.
Es viable verificar la trascendencia del software Wiris en otros temas de las matemáticas que incluye el software en comento, expuestas en la presente, para que se explote esta tecnología en otros ámbitos de la asignatura.