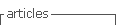INTRODUCCIÓN
Los Sistemas de puesta a tierra (SPT) son vitales dentro de las instalaciones eléctricas, dada su utilidad de proteger la integridad física de las personas y los equipos eléctricos y electrónicos, así como establecer una referencia de potencial para el sistema eléctrico. Un SPT proporciona un medio de conducción entre equipos e instalaciones y la tierra, de modo que las corrientes de falla van hacia esta [1], [2], [3].
Entre las variables que influyen en el diseño de un STP están la resistividad del suelo y la geometría de la malla, que determinan parámetros críticos que deben ser controlado, entre los cuales se encuentran [4]:
Corriente límite tolerable por el cuerpo
Voltajes de seguridad
Máximo potencial eléctrico de un electrodo de puesta a tierra con respecto a un punto de tierra lejano (GPR)
Voltaje de malla
Voltaje de paso
Voltaje de toque
Voltaje transferido
En el análisis de los STP es importante determinar la distribución de potencial en las regiones de este, para lo que se puede utilizar el método del tanque electrolítico y los métodos numéricos [5]. Dentro de los métodos numéricos se encuentra el de elementos finitos (FEM, del inglés finite element method), que facilita el análisis al dividir los cuerpos de un sistema en una cantidad finita de elementos, cada elemento está confinado entre nodos y dentro de cada elemento se asume un comportamiento continuo del fenómeno en estudio [6] [7].
En este contexto el FEM es permite resolver sistemas electromagnéticos complejos de manera gráfica, es decir, se dibuja las geometrías y se caracteriza los materiales involucrados en el fenómeno a estudiar, la solución será una distribución gráfica de los potenciales y el campo electromagnético asociado; por lo que este método se puede utilizar para resolver potenciales en los sistemas eléctricos [8], [9] incluyendo las mallas de puesta a tierra [10], [11], [12].
El diseño tradicional basado en las normas IEEE [1] considera geometrías cuadrangulares, que dificulta la aplicación cuando se requiere implementar geometrías diferentes. Dada la capacidad de procesamiento de los computadores, se puede utilizar programas gráficos de tipo FEM que permiten visualizar el comportamiento de un fenómeno físico, en este artículo se propone utilizar el FEM en tres dimensiones para el diseño de mallas de puesta a tierra. Para ello, se simulan sistemas de puesta a tierra en un suelo de varias capas y mallas de diferentes geometrías mediante el FEM con paquete de física eléctrica del programa Ansys.
Con el objetivo de obtener una metodología generalizada útil para la aplicación en el análisis de diseño de los STP, en este artículo se presenta el procedimiento de simulación y validación.
Para validar el método de simulación propuesto, en primer lugar, se construye un modelo real de un sistema de puesta a tierra con una malla a escala, de geometría rectangular de 900 mm x 900 mm con espacios de 45 mm. La malla se coloca en una cuba electrolítica para simular el comportamiento del suelo. Se utiliza una piscina de 4500 mm x 2200 mm x 800 mm.
Dentro de la cuba electrolítica se coloca una malla electrosoldada para establecer un área de referencia equipotencial. La cuba electrolítica está llena de agua para simular el comportamiento del suelo. La energía del sistema se obtiene de la red de suministro obteniendo un voltaje de 220 V / 60 Hz. Se regula la inyección de corriente hasta la obtención de 4 A. Se obtiene mediciones de los potenciales en el agua con un voltímetro y una sonda para medir voltaje. La sonda de voltaje se mueve en distintos puntos de la superficie de la piscina para obtener valores de voltaje. Estos valores de voltaje y sus coordenadas se grafican para visualizar el comportamiento del sistema a escala.
Luego se implementa un modelo digital del sistema a escala descrito. Se generan los elementos tridimensionales del sistema mediante AutoCAD, que son las entradas para la simulación en Ansys, en el que se configura la geometría y las características de los materiales del modelo físico. Posteriormente se contrastan los resultados de la simulación con los resultados obtenidos en el modelo físico. Se realizan adecuaciones en el tamaño del mallado y la calidad de los elementos tridimensionales hasta obtener una simulación eficiente. Se estudian los resultados obtenidos para generalizar el método de simulación.
Con el modelo validado se construyen modelos digitales a escala real utilizando la metodología propuesta. Se realizan diferentes casos de estudio variando la geometría, materiales y suelos. En los modelos simulados se cuantifica la resistencia de puesta a tierra, elevación de potencial a tierra SPT, voltaje de paso y de toque según las definiciones de la norma IEEE 80 [1].
METODOLOGÍA
Este estudio busca conocer la distribución del potencial eléctrico en una malla de puesta a tierra en un suelo compuesto por varias capas; con el objetivo de comprender de mejor manera cómo influyen las variables en el desempeño de una malla de puesta a tierra, en el voltaje de paso, en el voltaje de toque y también en la elevación de potencial de tierra o GPR. Para ello, se describen a continuación los métodos aplicados.
Definición del caso base
Se definió como caso base un modelo a escala de una malla de puesta a tierra cuadrada de 0,9 m x 0,9 m con cuadros de 4,5 cm; sumergida en una cuba electrolítica que simula el suelo y al que se inyecta una corriente por una de sus esquinas. El tamaño del tanque electrolítico se basó en el estudio presentado en [13].
El límite mínimo del factor de escala viene definido por la dimensión determinada en [13]. Donde se explica que el diámetro del hemisferio debe ser al menos el doble de la dimensión máxima de la cuadrícula (la diagonal). Según este enunciado para una cuadrícula de 90 m x 90 m el factor de escala sería al menos 85:1. En consecuencia se determina que el límite máximo del factor de escala está determinado por el tamaño del conductor. Para mayor comodidad al momento de la construcción, se eligió un factor de escala de compromiso de 100:1, de modo que, los metros en la cuadrícula real corresponden a centímetros en el modelo. Las pruebas experimentales indicaron que el tamaño del conductor tenía un efecto secundario en relación con los perfiles de potencial de la superficie; por lo tanto, la diferencia entre el factor de escala se consideró insignificante.
Circuito de medición
El circuito eléctrico que se utilizó para la toma de mediciones se detalla en la Figura 1. Este circuito eléctrico consta de un autotransformador variable de voltaje conectado directamente a la red eléctrica a frecuencia industrial. El variador de voltaje se encuentra acoplado mediante una conexión en serie a un reóstato, y también a la malla electrosoldada ubicada dentro de la piscina. Conectado a la fase del variador de voltaje, se encuentra la sonda de voltaje. Esta sonda de voltaje recorrió toda el área de la superficie de la piscina, y se procedió a realizar la adquisición de los datos.
Se utilizaron dos instrumentos de medición, una pinza amperimétrica y un voltímetro. La variable de entrada que se controló fue la corriente, mediante el uso de la pinza amperimétrica fue posible llevar el control para mantener constante el valor de la corriente en 4 A en todo momento de medición.
La sonda de voltaje conectada a un voltímetro, al ser móvil permitió obtener los valores superficiales de voltaje a lo largo de la piscina tanto en X como en Y al referirse a coordenadas cartesianas. Estos valores de voltaje y de corriente, fueron tabulados con su respectiva coordenada durante la toma de mediciones.
Construcción del modelo a escala
En etapa constructiva se definió un escalado de la malla de 90 cm por 90 cm. Se va a usar una cuba electrolítica que permite sumergir a la malla; el agua que está contenida dentro de la cuba representa el suelo. Y finalmente, la cuba electrolítica en el caso de estudio es una piscina. Las dimensiones del medio electrolítico comprenden 450 cm x 220 cm x 84 cm. En el contorno de la piscina está construido un semi domo, que es una malla que sirve para la de condición frontera de voltaje de cero voltios y está construida por una malla electrosoldada. Esta malla electrosoldada se conectó directamente al neutro del regulador de voltaje siendo un retorno para la corriente que será inyectada. En la construcción de la malla se utilizó un cable #24 AWG, las uniones de los cables fueron realizadas con estaño de soldar, la separación entre cables de la malla fue de 4.5 cm hasta llegar a obtener 20 divisiones.
Debido a la necesidad de que la malla sea sumergida, se utilizaron dos tubos PVC, que sirvieron de soportes para que pueda ser suspendida. La malla de puesta a tierra fue sumergida 0.6 cm bajo el nivel del agua, sostenida a los tubos mediante hilos nylon sujetados a cada una de las esquinas. Para la toma de mediciones se empleó una referencia móvil, en este caso un paralelepípedo de aluminio. La necesidad de realizar las mediciones en dos cuadrantes obligó a tomar como referencia fija un paralelepípedo de madera colocado a lo largo de la piscina. Al igual que el paralelepípedo de aluminio, se colocó una cinta métrica graduada en su cara superior. Esta cinta métrica graduada permitió en realizar movimientos calculados y toma de datos de manera precisa mediante el uso de una sonda de voltaje colocada a la referencia móvil.
Para manejar la conductividad del agua de la piscina se adicionó sal yodada, se decidió calentar agua y con el agua en temperatura de ebullición, se agregaron las fundas de sal y con un removedor se revolvió hasta que quedó completamente diluida. Al dejarla reposar por unos segundos, y sin rastro de que haya sal sin diluir se procedió a verter sobre el agua de la piscina; resultando una técnica efectiva y práctica para solucionar el problema que representaba mezclar la sal una vez instalados los elementos, tanto la malla como el semi domo. Para este proceso cada vez que se adicionaba una cantidad de sal diluida a la piscina, se tomaba medidas de la resistividad del agua. Se realizó este procedimiento varias veces hasta lograr una resistividad adecuada del agua para nuestro caso de estudio. Una vez definida la resistividad que se buscaba, se la controló durante el procedimiento de toma de datos paulatinamente. Se buscaba al realizar este permanente control es que la resistividad del agua no altere sus valores considerablemente y logre mantenerse lo más constante posible.
Para medir la resistividad del agua se usó un telurómetro calibrado y se procedió a aplicar el método de Wenner de 4 puntas [14]. Para asegurar que la medición sea lo más precisa posible, se tomaron varias medidas aleatorias para poder validar efectivamente que la resistividad se mantenga a lo largo del proceso. Estas variaciones fueron sometidas a diferentes distancias, y también a distintas horas del día.
La Tabla 1 presenta el método, y los distintos casos que se realizaron para la medición de la resistividad del agua. Se realizaron 3 mediciones, la profundidad a la cual se enterró las picas fue constante; la distancia de separación entre picas varió, por ello la lectura del telurómetro también lo hizo. Después de haber obtenido estos datos, se aplicó la ecuación del cálculo de la resistividad de Wenner [14].
Tabla 1: Valores de la profundidad de las picas, distancia de separación, lectura del telurómetro y la resistividad del agua de la cuba electrolítica
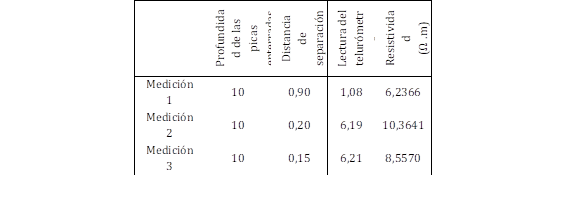
Estos resultados fueron promediados con el método BOX - COX para corregir la distribución de errores y varianzas desiguales [15]. Obteniendo un valor de resistividad de 9,1018 Ω.m que será usado posteriormente en la validación.
Validación de las simulaciones
Para realizar el proceso de validación se toman los datos característicos del experimento del modelo base, y se los aplica en una simulación en el programa Ansys con condiciones similares a la del experimento. Posterior a esto, para efectuar la validación. Se toman los valores medidos y se los importa directamente a MATLAB. Una vez que estos valores están cargados en MATLAB, se utiliza la herramienta CFTOOL que permite obtener los modelos de las curvas en tres dimensiones. Una vez cargado los datos del modelo físico, se carga también los datos del modelo experimental. Se evalúan los resultados de las curvas en las mismas coordenadas X e Y, y con los valores evaluados se determina las métricas de error: raíz del error cuadrático medio RMSE, error medio absoluto MAE, error relativo porcentual y error medio absoluto porcentual MAPE, que son medidas de desviación entre datos usado en estadística definidos y recomendados en [16].
Casos de estudio
Una vez que se valida el modelo a escala para garantizar que se puede utilizar el programa computacional Ansys se procede con la finalidad de comprender y entender que sucede al someter a una malla de puesta a tierra a distintos escenarios, para ello se han planteado varias situaciones para simularlas.
Entre los escenarios de simulación, se presentan: distintas configuraciones geométricas, distinta resistividad de los materiales, varias capas de suelo, diferentes valores de corriente que será inyectada en diferentes lugares de la malla.
Como variación de la configuración geométrica de una malla de puesta a tierra se van a tratar 3 casos: malla triangular, malla cuadrada y malla circular.
Respecto a la resistividad de los materiales, se tiene dos casos a tratar: cobre con 1.694E-08 Ω.m y aluminio con 2.67E-08 Ω.m.
Para la simulación se tomaron dos capas de suelo, la capa 1 de 4500 Ω.m y una profundidad de 5 m, y la capa 2 de 400 Ω.m y 10 m de profundidad. El suelo tendrá una temperatura de 22 º C.
Finalmente, las dos variaciones de corriente a utilizar son de 5 y 10 kA.
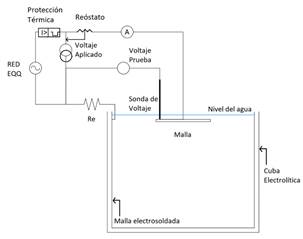
Se definieron 16 casos de estudio, para el desarrollo de este proyecto expresados de manera resumida en la Tabla 2. Para todos los casos, la profundidad de entierro de la malla es de 0,60 m, El objetivo de las simulaciones es observar los efectos de la geometría, de las resistividades de los materiales, del valor de la corriente, del lugar de inyección de la corriente y del número de capas. Para ello los casos de estudio son hipotéticos. Estas mallas no fueron diseñadas y el diseño no es del alcance de este proyecto. Al analizar los casos de estudio se puede evaluar las mallas para conocer si son o no adecuadas; y en caso de que fueran o no producto del diseño se pueda poner a prueba el diseño para evaluar su viabilidad.
RESULTADOS Y DISCUSIÓN
Validación de las simulaciones realizadas
Para la validación se tomaron cuatro índices de error detallados en 2.4. Los resultados de la simulación en Ansys exportados a MATLAB se grafican junto a los valores medidos en el experimento real y se obtienen las Figs. 2 y 3 se puede observar que el modelo real y el modelo simulado se aproximan bastante entre sí, considerando los errores de medición que pudo presentar el experimento al momento de realizar las mediciones, así como los errores de la simulación de FEM. También hay que tomar en cuenta la calibración de los equipos de medida, así también como errores humanos que pueden presentarse en el desarrollo de un proyecto.
Con los datos se puede constatar los indicadores de error para los valores medidos en el caso base y la simulación son aceptables.
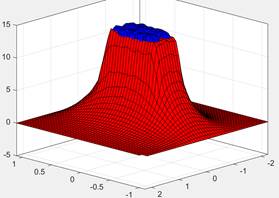
Figura 2: Vista lateral de la simulación de los errores del modelo real en color azul y el modelo simulado en color rojo
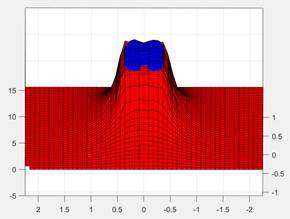
Figura 3: Vista frontal de la simulación de los errores del modelo real en color azul y el modelo simulado en color rojo
El valor RMSE es la raíz del error cuadrático medio, es el índice más empleado en modelos físicos. Ponderando los pronósticos más alejados al valor medido. Presenta un valor de 2,0635 voltios, que es bajo. El resultado obtenido del error medio absoluto o MAE calcula la magnitud promedio del error obtenido entre los datos estimados por el modelo y los datos medidos. En el caso del experimento presenta un valor 1,7882 voltios, que es bajo y aceptable. El indicador MAPE presenta un valor del 12,3242% que es aceptable para una aproximación, midiendo el error promedio de las estimaciones. Finalmente, como último indicador se presenta un error relativo porcentual igual al 3,2529% que es aceptable y bajo.
Estos valores de los indicadores significan que el modelo simulado y la realidad están bastante cerca, por lo que se puede aceptar el modelo de ANSYS como válido para analizar un SPT mediante FEM, y una vez validado se procede entonces a simular casos de estudio reales.
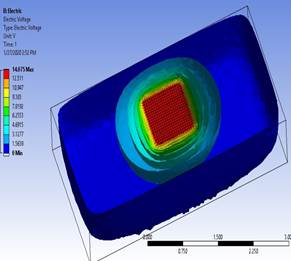
Figura 4: Resultados del potencial eléctrico del caso base del experimento visualizando como curvas equipotenciales de voltaje.
En la Fig. 4 se puede visualizar desde una perspectiva ubicada sobre el experimento, las curvas equipotenciales que se producen para despejar la corriente de falla en el suelo en Ansys.
Resultados de los casos de estudio
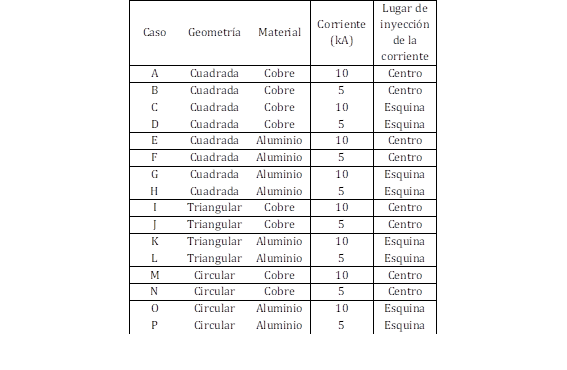
Se visualiza en la Tabla 3 la cantidad de elementos finitos, y la cantidad de elementos obtenidos en los casos de estudio.
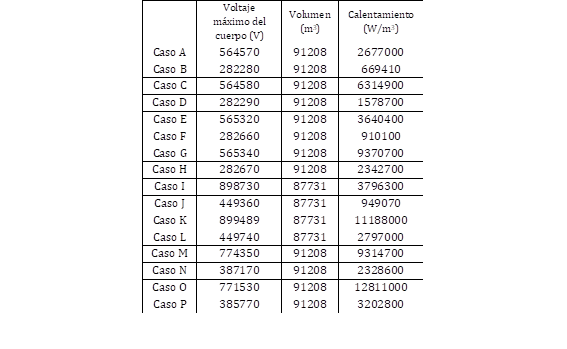
En la Tabla 4 se presentan los resultados de los voltajes máximo del cuerpo de simulación, el volumen obtenido y el calentamiento.
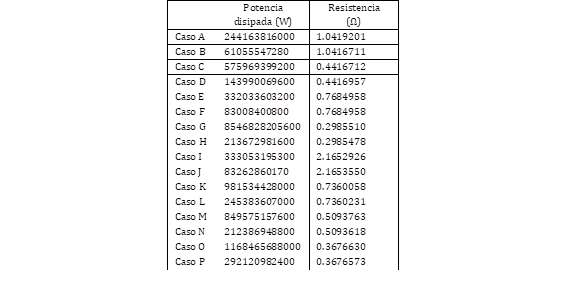
En la Tabla 5 se presentan los resultados obtenidos de la potencia disipada, además de la resistencia de puesta a tierra de la malla.
El voltaje de paso y de toque tolerables para personas de 50 y 70 kg se calculan como se define en IEEE 80 [1] sin una capa superficial es decir (s= ( del suelo y CS=1, y sus resultados son:
Epaso50=3248 V.
Etoque50=899 V.
Epaso70=4396 V.
Etoque70=1216.75 V.
Finalmente, en la Tabla 6 se presentan los resultados obtenidos del voltaje de paso, voltaje de toque y GPR de la simulación.
Tabla 6: Resultados de la obtención de los voltajes de paso, voltajes de toque y GPR de las simulaciones de Ansys
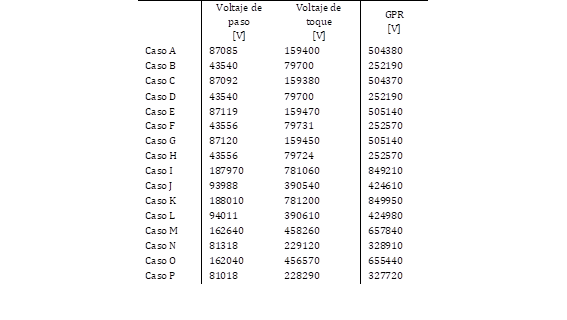
Discusión sobre Voltaje máximo de los cuerpos simulados
Se puede inferir que no es determinante el punto de inyección de la corriente en la malla. Esto quiere decir que se mantendrá el mismo nivel máximo de voltaje. Se cumple si se mantiene la configuración geométrica, la resistividad del material, y el valor de corriente constantes y se puede constatar también en el resto de los casos, como por ejemplo en el caso B - D, y el caso E - G.
Discusión sobre Voltajes máximos de la superficie del suelo (GPR)
El voltaje máximo de la superficie del suelo es el voltaje que se produce únicamente en la capa superficial del suelo en donde se encuentra enterrada la malla de puesta a tierra.
Estos voltajes tienen una relación similar a los voltajes de todo el cuerpo que se simularon, con la diferencia que son de menor valor. Se logra determinar que no es concluyente el punto de inyección de la corriente en la malla. Esto quiere decir que se mantendrá el nivel máximo de voltaje. Se cumple si se mantiene la configuración geométrica, la resistividad del material, y el valor de corriente constantes.
Discusión sobre Resistencia de la malla de puesta a tierra
Analizando una malla de puesta a tierra que posee la misma configuración geométrica, el mismo material, y el punto por el cual ingresa la corriente a la malla es el mismo genera un resultado peculiar. En el caso específico de la malla de puesta a tierra de configuración cuadrada, material de aluminio, numero de capas 2, la corriente es inyectada en la parte central de la malla. Se diferencian únicamente en el siguiente aspecto el caso E la corriente es de 10 kA y en el caso F la corriente es de 5 kA.
Se puede determinar que el valor de la resistencia de puesta de malla a tierra es independiente del valor de la corriente inyectada al ser calculada por medio de la potencia disipada. Por el contrario, el valor de la resistencia de puesta de malla a tierra varia si se emplean diferentes materiales, geometría, o el lugar de inyección de la corriente varia.
Finalmente, en la resistencia de puesta a tierra influye donde está siendo inyectada la corriente. Se puede mencionar que la fuente de corriente ve diferentes impedancias según el lugar donde se la inyecte. Al inyectarse dos corrientes en el mismo punto se vera la misma impedancia, pero al inyectarla en un punto diferente el valor de impedancia cambiará.
Discusión sobre el voltaje de paso
Para estudiar los resultados de voltaje de paso se tiene que malla de puesta a tierra que posee la misma configuración geométrica, mismo valor de la corriente, y el punto por el cual ingresa la corriente a la malla es el mismo genera un resultado analizar. En el caso específico de la malla de puesta a tierra de configuración triangular, número de capas 2, y un valor de corriente igual a 10 kA. Se diferencian en dos aspectos el caso I el material de construcción el cobre y en el caso K la construcción del material es aluminio.
Se puede concluir que el valor del voltaje de paso máximo no depende en gran medida de la resistividad del material como se puede visualizar por ejemplo en los casos A - E y caso I - K, e independiente del lugar en donde se produzca la falla como por ejemplo en los casos A - C y caso E - G. Pero al tener un distinto valor de corriente o geometría este valor cambia, además depende directamente de la resistividad del suelo.
En el caso de simulación el suelo tratado no contaba con una superficie de protección donde (s= ( y el tiempo de duración de la falla fue de 1 segundo.
El voltaje de paso según la norma ANSI / IEEE Std 80-2013 está definido para dos casos en específico una persona con un peso de 50 kilogramos y 70 kilogramos. La norma brinda un criterio de voltaje de paso tolerable.
Al analizar los resultados obtenidos y compararlos con los tolerables se observa que estos valores obtenidos en el caso experimental son mayores a los tolerables. Lo que quiere decir que la malla de puesta a tierra simulada no es segura.
Por lo tanto, si la malla fuera producto de un diseño real se obtendría como evaluación que es insegura y se debería entonces elaborar un diseño adecuado del SPT que permita cumplir con este valor tolerable, ampliar el área de cobertura de la malla de puesta a tierra puede ser una opción de solución.
Discusión sobre el voltaje de toque
Al analizar los resultados obtenidos del voltaje de toque máximo en la Tabla 6 de las simulaciones realizadas presenta una particularidad, este valor de voltaje de toque es igual en los casos en los cuales la corriente de ingreso a la malla de puesta tierra es la misma.
Es decir, el valor del voltaje de toque máximo se mantiene constante sin importar el lugar por el cual es inyectado. Esto se cumple únicamente si la configuración geométrica se mantiene, si el valor de la corriente es idéntico, y si además depende directamente de la resistividad del suelo. Se presenta un valor de voltaje de toque superior al voltaje de paso, que excede al valor tolerable admisible de voltaje de toque. Se debería hacer cambios y volver a simular para mejorar los diseños.
El voltaje de toque según la norma ANSI / IEEE Std 80-2013 está definido para dos casos en específico una persona con un peso de 50 kilogramos y 70 kilogramos. La norma brinda un criterio de voltaje de toque tolerable. Al analizar los resultados obtenidos y compararlos con los tolerables del caso simulado de estudio, se observa que estos valores obtenidos en las simulaciones son mayores a los tolerables. Lo que quiere decir que la malla de puesta a tierra simulada no es segura. Por lo tanto, si la malla fuera producto de un diseño real se obtendría como evaluación que es insegura y se debería entonces elaborar un diseño adecuado del SPT que permita cumplir con este valor tolerable, ampliar el área de cobertura de la malla. Se debería hacer cambios y volver a simular para mejorar los diseños.
Perfiles de voltaje de las mallas
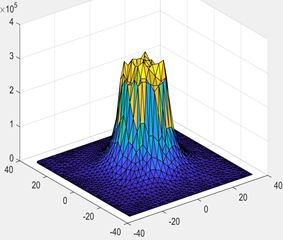
Como se observa en las Figs. 5, 6 y 7 los perfiles de voltaje toman la forma de su configuración geometría. Es decir, Es decir, la Figura 5 posee una forma geométrica cuadrangular, la Fig. 6 posee la forma geométrica de una figura triangular, y finalmente la Fig. 7 posee una forma geométrica circular. En estas gráficas, el plano superficial es el suelo y la altitud de las gráficas representa el voltaje en cada punto del espacio simulado.
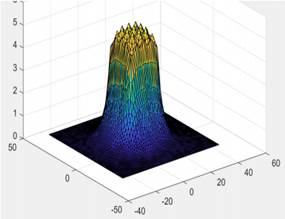
Figura 5: Grafica en tres dimensiones de los voltajes de la malla de puesta a tierra cuadrada del caso A
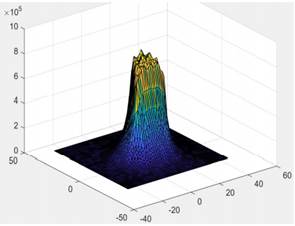
Figura 6: Grafica en tres dimensiones de los voltajes de la malla de puesta a tierra triangular del caso K
Las caras donde fueron definidas la condición de frontera presentan un valor muy cercano a cero, mientras se va acercando el valor a la malla este va aumentando hasta llegar a unos valores picos en el interior de la puesta de malla a tierra.
El perfil de voltaje muestra como la malla de puesta a tierra se eleva de voltaje cuando despeja una falla; cuando existe una descarga que cae por la malla, todos los valores que comprenden el área de la malla suben de voltaje mientras que los lugares lejanos a esta se quedan con un potencial de cero. Esta elevación del potencial dentro de la malla de puesta a tierra puede ser peligroso para una persona. Si el individuo se encuentra sobre la malla, al caminar sus pasos generan una diferencia de potencial. Si valores obtenidos están sobre los valores de voltaje de paso tolerables generan un alto riesgo para la vida de la persona.
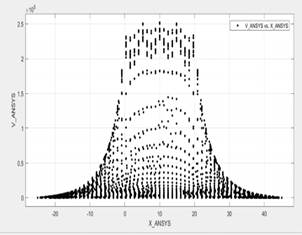
Figura 8: Visualización de los datos medidos en la coordenada X versus los voltajes obtenidos. Caso B.
En la Fig. 8 se observa una malla de puesta a tierra de configuración geométrica cuadrada en dos ejes de coordenadas: en el eje de las abscisas se encuentra el valor adquirido en las mediciones a lo largo de la coordenada X, mientras que en el eje de las ordenadas el valor de voltaje que brindó la simulación. La Figura 9 presenta el perfil de voltaje de una malla triangular.
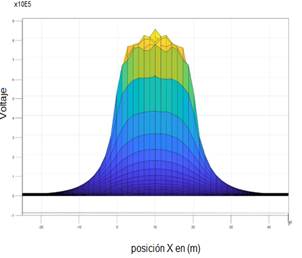
Figura 9: Perfil de voltajes visto de una malla de configuración triangular al ser inyectado con 10 kA de corriente caso I.
De acuerdo con las simulaciones obtenidas mediante el análisis de las curvas de perfil de voltaje, se observa que el voltaje de toque y paso se encuentran relacionados. Un perfil de voltaje llano es un perfil seguro, al poseer características escarpadas con pendientes elevadas genera voltajes de paso y voltajes de toque más peligrosos, como se visualiza en la Tabla 6 de los resultados de los casos de estudio.
En los casos de estudio, la malla de puesta a tierra de menor área es la configuración geométrica circular. Al querer despejar el mismo valor de corriente, deberá despejar la falla con un área menor y por lo tanto producirá voltajes elevados al tener menos espacio. En consecuencia, el voltaje de toque y paso dependerán de la cantidad de corriente inyectada, resistividad del material y la geometría
Efecto de la variación de las resistividades del suelo
Cuando la malla se ubica en un medio más conductivo, el GPR se reduce. Esto se debe a que, con menor resistencia, la misma corriente produce un voltaje menor. Se puede notar también que existe un patrón de variación de voltaje más brusco cuando el medio más conductivo está abajo, es decir la capa inferior tiene menor resistividad; esto implica mayores voltajes de paso.
Se entiende que la posición de las capas de suelo tiene gran influencia en los sistemas de puesta a tierra. Se debe procurar que la malla se ubique en el medio más conductivo. Futuros estudios deben enfocarse en combinar los principales suelos del país para facilitar el diseño de sistemas de puesta a tierra.
CONCLUSIONES Y RECOMENDACIONES
Según los resultados obtenidos la posición y resistividad de las capas de suelo tienen gran influencia en los Sistemas de Puesta a Tierra. En relación con lo expuesto, diferentes suelos causan diferentes GPR y diferentes voltajes de paso; son más altos cuando la capa de suelo en la cual se encuentra la malla tiene mayor resistividad. En conclusión, la posición y la resistividad de los suelos sí afectan a los Sistemas de Puesta a Tierra y se puede utilizar el método FEM de este proyecto para predecir los efectos de este fenómeno.
De acuerdo con los resultados tabulados en la Tabla 4 en los casos A y C se observa que el punto de inyección de corriente no causa cambios significativos en los voltajes de los sistemas de puesta a tierra. Para fines prácticos, los voltajes de paso, de toque y GPR se distribuyen de maneras iguales. Por otro lado, se puede observar que el calor generado es diferente. En conclusión, los voltajes distribuidos no dependen del punto de inyección dentro de la malla mientras que el calibre del cable del Sistema de Puesta a Tierra tenga la capacidad conducir la corriente de la falla.
Se puede observar en la Tabla 6 que para los casos A y B que la intensidad de la corriente inyectada causa cambios significativos en los voltajes de los Sistemas de Puesta a Tierra. Numéricamente, los voltajes de paso, de toque y GPR incrementan junto con la corriente inyectada. En conclusión, la corriente que disipa un Sistema de Puesta a Tierra afecta directamente a los voltajes que se deben controlar y por lo tanto es un parámetro que se debe definir durante el diseño del sistema.
Al comparar los casos A, I y M en la Tabla 6 se nota que el voltaje de toque, paso y GPR en un sistema de puesta a tierra aumentan con la existencia de ángulos agudos. Adicionalmente, la malla redonda tiene menos conexiones internas que las mallas cuadrada y triangular; aun así, logra dar mejores valores que la triangular. Se concluye que una malla no necesita tener mucho cable para ser eficiente; en su lugar debe tratar de cubrir la mayor cantidad de área posible y evitar en lo posible ángulos agudos.