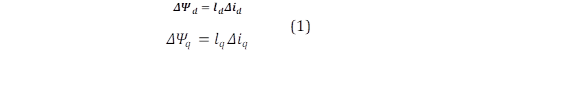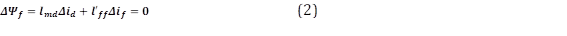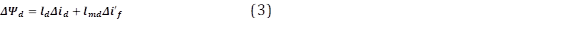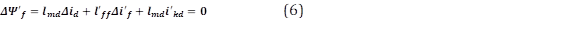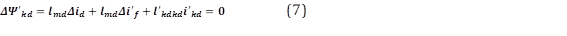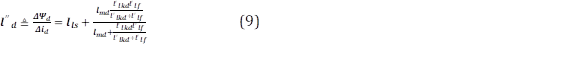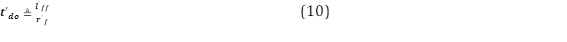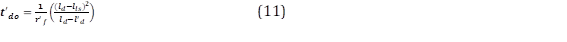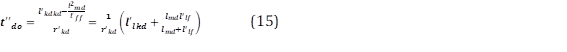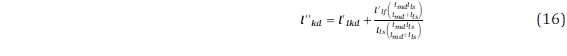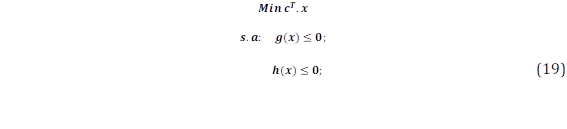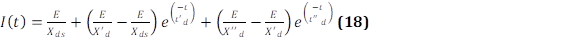INTRODUCCIÓN
La mayor parte de la energía eléctrica generada en el mundo se realiza con máquinas sincrónicas, siendo su estudio, desarrollo matemático y adecuada representación temas de gran importancia que han venido evolucionando con los años con el propósito de poder predecir el comportamiento de los sistemas eléctricos y así mejorar sus condiciones de operación . El avance de la ingeniería eléctrica ha desarrollado estudios con la finalidad de simular a la máquina sincrónica, bajo condiciones de operación, contingencia, falla y conectada a diferentes sistemas o en vacío; todos estos estudios utilizan modelos matemáticos que representan físicamente a la máquina sincrónica .
Los modelos matemáticos de la máquina sincrónica son la representación de sus ecuaciones de movimiento y de las relaciones de voltajes y corrientes entre sus partes constitutivas. Uno de los modelos más conocidos contiene ecuaciones con los parámetros eléctricos en valores de reactancias, resistencias y constantes de tiempo, y de estos valores dependen las respuestas de la máquina en el modelo de representación establecido para las diferentes simulaciones . Los valores de los parámetros que definen las ecuaciones dentro del modelo para cualquier elemento de simulación infieren directamente en la respuesta de este elemento. Para encontrar los parámetros de la máquina sincrónica, se aplica la normativa IEEE Std 115 , la exactitud de los valores depende directamente de los recursos del laboratorio y de la interpretación y correcta aplicación de la norma.
El Laboratorio de Máquinas Eléctricas de la Escuela Politécnica Nacional posee recursos limitados para realizar estas mediciones y los elementos de medida tienen baja exactitud y sensibilidad, por ello, los resultados de las pruebas no son confiables y se los asume como una aproximación hacia los valores que deben tener para representar correctamente a la máquina sincrónica.
Los valores obtenidos deben ser sintonizados al modelo de la máquina sincrónica, y entregar una respuesta similar a la respuesta experimental de la máquina frente a una perturbación aplicada. Para realizar la perturbación se elige la aplicación de un voltaje de campo y un cortocircuito trifásico en los bornes de la armadura y se analiza el voltaje de la armadura y la corriente de línea para realizar esta sintonización.
El proceso de sintonización se realiza con la herramienta computacional Estimación de Parámetros de MATLAB-Simulink, que utiliza métodos de optimización para estimar los valores de los parámetros eléctricos. La convergencia del método de optimización, el menor valor para una función de costo o error y la similitud entre los oscilogramas de respuesta experimental y respuesta de simulación indican conjuntamente los valores de los parámetros sintonizados.
Este documento presenta en la Sección 2 los conceptos básicos del modelo de un generador sincrónico y de los métodos de optimización para estimación de parámetros. La Sección 3 contiene la metodología propuesta en la que se ajustarán los resultados obtenidos de dos perturbaciones realizadas al generador utilizando como parámetros de partida los valores obtenidos con pruebas estandarizadas de laboratorio. La sección 4 presenta los resultados del estudio para diferentes métodos de optimización y la sección 5 presenta las conclusiones del documento.
MARCO TEÓRICO
Parámetros Eléctricos de la Máquina Sincrónica
Los parámetros de la máquina sincrónica se presentan en forma de inductancias, constantes de tiempo y resistencias. La mayoría de las pruebas se derivan de las medidas tomadas en los devanados de la armadura y dependen de las constantes de tiempo entre la etapa transitoria y subtransitoria .
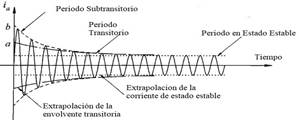
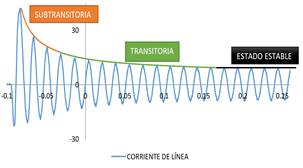
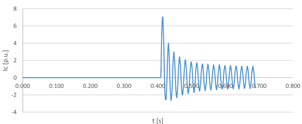
Una demostración muy usada de este fenómeno es el oscilograma de cortocircuito en las corrientes de la armadura mostrado en la Fig. 1, donde el cortocircuito trifásico es aplicado en los terminales del devanado de armadura inicialmente en circuito abierto con excitación constante.
La corriente de cortocircuito está definida por tres periodos, como se observan en la Fig.1: el periodo subtransitorio se establece en los primeros ciclos del corto circuito cuando la corriente decae muy rápido relacionado principalmente a los cambios de corriente en los devanados de amortiguamiento. El periodo transitorio ubicado en los siguientes ciclos donde la corriente decae lentamente y es relacionado principalmente a los cambios de corriente en los devanados de campo del rotor y el periodo de estado estable en los ciclos donde la corriente de cortocircuito se estabiliza en un valor diferente a la corriente previa al cortocircuito .
Variación Instantánea de Enlaces de Flujo y su Relación con la Corriente
Cuando el valor pico de la fuerza magnetomotriz (Fmm) giratoria se alinea con el eje directo, la relación entre el enlace de flujo y la corriente en el eje directo da como resultado la inductancia sincrónica l 𝑑 , de igual manera se podría encontrar la inductancia sincrónica del eje en cuadratura 𝑙 𝑞 . Un cambio en las concatenaciones de flujo 𝛥𝛹 𝑑 o 𝛥𝛹 𝑞 en la operación sincrónica donde todas las corrientes del devanado del rotor son permanentes, va acompañado de un cambio en las corrientes correspondientes 𝑖 𝑑 o 𝑖 𝑞 , reflejado en (1). Se observa que la inductancia efectiva para 𝑖 𝑑 es 𝑙 𝑑 [4].
Inductancias Transitorias
Las resistencias de los devanados de amortiguamiento son usualmente mayores que las resistencias de los devanados de campo y como consecuencia las corrientes inducidas en el devanado amortiguador decaen con mayor velocidad que las corrientes de los devanados de campo [4]. Se considera los cambios en los enlaces de flujo de los devanados sobre el eje directo, con 𝛥 𝛹 𝑓 =0 y 𝛥 𝑖′ 𝑘𝑑 =𝛥 𝑖′ 𝑘𝑞 =0 como muestra (2) y (3).
Eliminando la variación de corriente de campo para expresar 𝛥 𝛹 𝑑 solamente en términos de 𝛥 𝑖 𝑑 se tiene (4) y posteriormente se encuentra la inductancia (5).
Inductancias Subtransitorias
Para el periodo subtransitorio, las corrientes inducidas en los devanados del rotor mantienen el enlace de flujo inicialmente constante en el rotor con el eje directo [4], con esta consideración se cumple que 𝛥𝛹′ 𝑓 =𝛥 𝛹′ 𝑘𝑑 =0 para obtener (6), (7), y (8):
Sustituyendo el modelo de los cambios de corriente en (6), (7), y (8), y definiendo la relación entre 𝛥𝛹 𝑑 y 𝛥𝑖 𝑑 como la inductancia subtransitoria del eje directo 𝑙′′ 𝑑 , se obtiene (9):
Constantes de Tiempo Transitorio
Asociado a los dos periodos de los devanados del rotor en la máquina hay dos diferentes constantes de tiempo, las constantes que tienen un valor mayor se encuentran en el periodo transitorio, mientras las de menor valor se encuentra en el periodo subtransitorio [4].
Con la armadura en circuito abierto e ignorando los efectos de los devanados de amortiguamiento que contienen el mayor valor de resistencia, el cambio en las corrientes de campo en respuesta a los cambios en los voltajes de excitación es gobernado por las constantes de tiempo del circuito abierto, definido como en (10), [4]:
Sin embargo, cuando se cortocircuitan los devanados del rotor y de la armadura y se ignora los efectos de los devanados de amortiguamiento, la inductancia aparente del devanado de campo varía de acuerdo a la conexión externa. La relación entre las constantes de tiempo del devanado de campo con los devanados de la armadura en cortocircuito y en circuito abierto, es igual, a la relación de la inductancia aparente vista por la corriente de la armadura con el campo cortocircuitado y en circuito abierto dada en (11), [4].
Constantes de Tiempo Subtransitorio
La constante de tiempo subtransitoria en circuito abierto del eje directo, t ′′ 𝒅𝒐 , es la constante de tiempo de la corriente en el devanado de amortiguamiento cuando los terminales del devanado de campo están cortocircuitados y los devanados de la armadura se encuentran en circuito abierto. La constante de tiempo subtransitorio también puede ser definida como el tiempo en segundos necesario para que la componente inicial de voltaje simétrico en el eje directo decrezca rápidamente a 𝟏 𝒆 de su valor inicial; cuando el cortocircuito en los terminales de la armadura con la máquina girando a velocidad sincrónica es despejado [4]. Durante este periodo inicial de decaimiento del voltaje en el circuito abierto de la armadura la resistencia del devanado de campo es despreciada y la inductancia efectiva para la corriente del devanado de amortiguamiento bajo estas condiciones está dado en (12) a (15), [4]:
La constante de tiempo subtransitoria para cortocircuito del eje directo, 𝑡 ′′ 𝑑 , es la constante de tiempo de la corriente del devanado de amortiguamiento cuando los circuitos de armadura y campo se encuentran cortocircuitados, dados en (16) y (17), [4].
Estimación de Parámetros basado en Métodos de Optimización en MATLAB-Simulink
La estimación de parámetros, conocido también como Identificación de Sistemas, se constituye en una herramienta útil que permite determinar los parámetros de los modelos matemáticos de una manera eficiente y con precisión para representar adecuadamente el comportamiento de un sistema basado en datos experimentales. El proceso de identificación de parámetros es un proceso de optimización que se basa en que repetidamente se calculan los parámetros de un modelo para satisfacer una función objetivo y restricciones, y se compara la respuesta simulada con la respuesta medida para así establecer si el modelo es aceptable o no. Los métodos utilizados en ingeniería para realizar optimización de bases de datos son diversos y muy extensos. En esta sección se revisará los métodos que utiliza la herramienta computacional de Estimación de Parámetros de MATLAB-Simulink.
Gradiente descendente
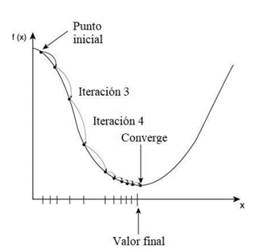
El método iterativo del gradiente descendente es una variación de la regresión lineal y utiliza una función lineal para describir la función resultante de un estudio ya que punto a punto los valores de sus parámetros se ajustan a la función lineal como se observa en al Fig.2. En cada iteración modifica los valores de un vector de parámetros, el cual está formado por los valores propios de los parámetros y sus derivadas parciales (vector gradiente) y se puede utilizar este método con matrices para varias dimensiones . Del ajuste de los valores iniciales del vector de parámetros depende la convergencia del método. La inicialización de parámetros también afecta al tiempo en que el método converja y pueden ser minutos, horas, días e inclusive semanas. Los valores iniciales no pueden ser cero, tampoco pueden adquirir valores demasiado grandes y pueden ser valores aleatorios pequeños .
Punto interior
En el algoritmo de optimización de punto interior se tienen condiciones de igualdad y desigualdad, cumpliendo con la función representada en (18) de un problema de programación lineal .
Donde c, x, g(x), h(x), representan: el vector de coeficientes de costo, parámetros del problema en c, vector de restricciones lineales de igualdad, vector de restricciones lineales de desigualdad, respectivamente. Para la solución de este tipo de problemas el método de punto interior realiza una transformación y aproxima el problema únicamente a condiciones de igualdad .
Programación cuadrática secuencial, SQP
Es un método iterativo que ayuda a la solución de problemas de programación no lineal, en donde la función objetivo es cuadrática y contiene dos variables que la definen, pero está sujeta a restricciones lineales. El método modeliza cada una de las variables de la función objetivo como una aproximación de la programación cuadrática, utilizando multiplicadores de LaGrange y expansiones de Taylor para en cada iteración ir aproximando cada variable de la función objetivo a las condiciones de paro. En este método también es muy importante los valores iniciales que tomen los parámetros y el error que se desea obtener de acuerdo a ello se tendrá una relación directa con el tiempo que tome para la convergencia del método, este método utiliza un tiempo menor gracias a la segunda derivada que el método anterior .
Trust region reflective
También denominado de paso restringido, donde la forma de aproximación hacia el menor valor de la función objetivo, ya no es lineal y utiliza una función cuadrática adicional para delimitar la región de acción en forma de elipse. Utiliza el método de minimización sin restricciones, es decir, la evaluación de la aproximación hacia las condiciones de paro se realiza en cualquier dirección y no con tendencia lineal de descenso. Transforma el vector de dirección en valores escalares y dentro de cada iteración evalúa puntos al azar dentro y fuera de la región, con diferentes distancias desde los límites de la región y lo puntos que cumplan con un menor valor para la función objetivo son encerrados por una nueva región de confianza de menor diámetro para la siguiente iteración hasta cumplir con las condiciones de paro. Para cumplir con la región de confianza utiliza aproximaciones de Taylor y el gradiente de los parámetros, y con esta información, adicional con otros elementos poder formar la matriz Hessiana que considera derivadas parciales hasta de segundo orden .
Levenberg - Marquardt
Es un método iterativo de igual manera descendente hacia el menor error con la diferencia que ha sido diseñado para trabajar específicamente con las funciones de error expresadas como sumas de errores cuadráticos .
Symplex y Pattern Search
El método de patrones de búsqueda de Hooke-Jeeves crea un conjunto de direcciones de manera iterativa, con un algoritmo donde incorpora una secuencia de iteraciones en la generación de una nueva dirección de búsqueda. El algoritmo combina movimientos exploratorios y movimientos de patrones con alguna heurística. Los movimientos exploratorios examinan la vecindad del punto actual para encontrar el mejor punto alrededor del mismo. Por lo tanto, los movimientos exploratorios examinan el comportamiento local de la función y buscan localizar la dirección de cualquier pendiente existente en la zona. La diferencia entre la búsqueda simplex y pattern radica en que la búsqueda simplex no respeta limites inferiores. Ambos métodos trabajan con algoritmos de búsqueda de patrones dentro del conjunto activo de la función error u objetivo, pero para el método simplex la forma de búsqueda es lineal, mientras para el método pattern se pueden tener distintas formas de búsqueda .
METODOLOGÍA
La metodología propuesta en este documento consiste en ajustar los parámetros del generador sincrónico utilizando las herramientas de optimización descritas en la sección 2.2 y así minimizar la diferencia entre las señales medidas y simuladas. Los métodos de optimización permiten sintonizar modelos matemáticos a sus parámetros que los caracterizan, para ello el modelo matemático debe existir físicamente y tener un punto de comparación entre el modelo matemático y el fenómeno físico . El concepto se representa en la Fig.3.
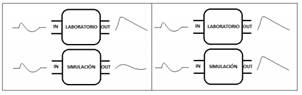
Figura 3: Concepto de estimación de la respuesta de un modelo físico. Izquierda: con optimización. Derecha: con optimización.
Se analiza el comportamiento de la máquina sincrónica representada como una función de transferencia en dos situaciones; la máquina físicamente en laboratorio y la máquina representada por un modelo matemático. En la parte izquierda se observa la respuesta de los dos casos sin optimización, en la parte derecha se observa las respuestas de los casos anteriores aplicados un método de optimización. El método de optimización ayudará a disminuir los errores de pruebas o estudios realizados para obtener el modelo matemático de la máquina sincrónica y sus parámetros eléctricos; entregando como resultado un modelo matemático y parámetros eléctricos que reflejan el comportamiento físico de la máquina sincrónica. Como condición inicial en el modelo de la máquina sincrónica seleccionada se realizaron pruebas estándar, basadas en IEEE Std 115, descritas a continuación. Para finalizar se aplica el método de optimización para la sintonización de los parámetros eléctricos con las respuestas de laboratorio ante dos perturbaciones y su simulación.
Pruebas de Laboratorio para Obtener los Parámetros Eléctricos de la Máquina Sincrónica
Se presentan los fundamentos y procedimientos de las pruebas aplicadas para la obtención de parámetros eléctricos necesarios para este estudio bajo la norma IEEE Std 115 - 2009 .
Prueba de saturación en circuito abierto
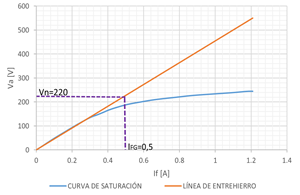
Se controla a la máquina a velocidad nominal, sin carga, en circuito abierto; tomando simultáneamente medidas de voltaje línea-línea de armadura, corriente de campo y frecuencia o velocidad de rotor, se puede construir la curva de saturación en circuito abierto y la línea de entrehierro, en la Tabla 1 se muestra la forma de obtener las mediciones necesarias [3]. La línea de entrehierro se obtiene extendiendo la parte lineal de la curva de saturación de circuito abierto. Cuando la curva de vacío obtenida no corta en el origen debido al voltaje remanente, se realiza una corrección trazando la línea de entrehierro hasta encontrar el punto de intersección con el eje de la corriente de campo. El valor de corriente de campo desde el origen hasta el punto de intersección hallado, representa el valor de corrección que debe ser sumado a todos los valores medidos de la corriente de campo, como muestra la Fig. 4.
Prueba de saturación en cortocircuito
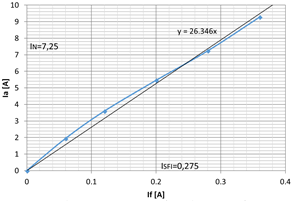
Las condiciones iniciales de la prueba de saturación en cortocircuito consisten en llevar a la máquina a velocidad nominal, sin carga, donde se aplica un cortocircuito trifásico sostenido en los terminales de armadura. Se debe registrar simultáneamente medidas de corriente de línea en armadura y corriente de campo como muestra el procedimiento de la Tabla 2 [3]. Como consideraciones generales, las lecturas para la curva mostrada en la Fig. 5 deben siempre ser tomadas en orden descendente, para evitar efectos de calentamiento y errores en la medición la lectura mayor debe ser tomada primero.
Prueba de deslizamiento
La prueba de deslizamiento consiste en hacer girar al rotor a una velocidad ligeramente diferente a la sincrónica, con el circuito de campo en circuito abierto y la armadura alimentada por una fuente trifásica de secuencia positiva y a frecuencia nominal [3].
El procedimiento consiste en registrar oscilogramas de la corriente de línea en armadura, voltaje línea-línea de armadura y voltaje a través del devanado de campo en circuito abierto cuando la fuente de voltaje trifásica se selecciona en un valor de voltaje que se encuentre por debajo del punto cruce entre la línea de entrehierro y la curva de saturación de vacío. Se debe tomar las mediciones en el cruce por cero, el deslizamiento se define como la relación de la frecuencia del voltaje inducido en el campo a la frecuencia del voltaje aplicado, observados en las Fig. 6 y 7.
Prueba de cortocircuito trifásico
La prueba de cortocircuito se define como el análisis de los componentes de la corriente de línea que entrega la máquina en el devanado de armadura antes, durante y después de la aplicación de un cortocircuito trifásico de duración de 0,5 segundos en los terminales de los devanados de armadura [3]. Las condiciones de funcionamiento de la máquina son: voltaje nominal línea-línea en circuito abierto y sin carga, girando a velocidad nominal. Se obtiene una respuesta que se ajusta al comportamiento de la ecuación (18).
Como se observa en la ecuación (18) y la Fig. 8 la corriente de cortocircuito trifásico súbita está constituida de tres partes, un primer término constante y dos términos de comportamiento exponencial, donde los valores del tercer término decaen con mayor velocidad que los valores del segundo término, la porción curva donde los valores decrecen con mayor velocidad es la etapa subtransitoria, la porción recta donde los valores decrecen con menor velocidad es la etapa transitoria de la curva y la porción donde los valores se mantienen constantes se denomina estado estable.
Prueba de recuperación de voltaje
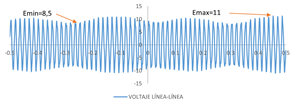
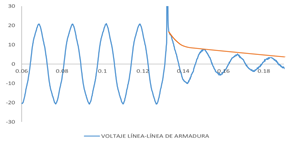
La prueba de recuperación de voltaje tiene por objetivo analizar las componentes transitorias y subtransitorias de voltaje al momento de abrir una falla sin carga trifásica sostenida en los devanados de armadura, se utiliza el mismo circuito que la prueba de cortocircuito trifásico [3]. Previo al despeje de la falla se toman los valores de corriente de línea en las fases y voltajes RMS línea-línea de armadura, con la máquina girando a velocidad sincrónica y con un valor de excitación de campo seleccionado en la porción lineal de la curva de saturación de circuito abierto. La obtención de los oscilogramas de los voltajes línea-línea de armadura de realiza durante la apertura del interruptor tripolar se muestra en la Fig. 9.
Prueba de cortocircuito súbito línea a línea
La prueba de cortocircuito línea a línea tiene un proceso muy similar a la prueba de cortocircuito trifásico, tomando las mismas medidas en dos fases, se lleva a cabo cortocircuitando dos terminales de la máquina, que deberá estar operando a velocidad nominal y sin carga, se mide el voltaje de circuito abierto en p.u., antes del cortocircuito, y el valor rms de la componente alterna inicial de la corriente de armadura I'' [3], en la Fig. 10 se observa la misma naturaleza de respuesta para la prueba de cortocircuito súbito línea-línea, que para la corriente de cortocircuito trifásico súbito.
Prueba de desconexión de bajo voltaje aplicado en armadura a un bajo deslizamiento
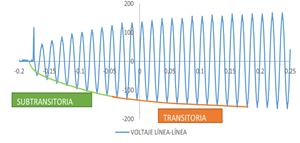
La prueba de desconexión de bajo voltaje aplicado en la armadura a un muy bajo deslizamiento, se realiza cuando la máquina tiene un deslizamiento bajo con una fuente trifásica operando en el rango de 5% -10% del voltaje nominal de armadura y a frecuencia nominal, el circuito de prueba es el mismo que para la prueba de deslizamiento [3]. Para la desconexión súbita se debe determinar que la posición del rotor se encuentre en el eje en cuadratura, lo que permite registrar corrientes de línea y voltaje línea-línea en la armadura. Se observa al instante de la desconexión que el voltaje línea-línea de armadura cae súbitamente a un valor particular y luego decae gradualmente hasta un valor no menor al 20% del voltaje aplicado, como se observa en la Fig. 11.
Prueba de rechazo de carga
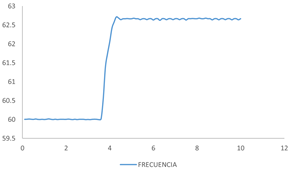
Para la realización de la prueba de rechazo de carga, se tiene al generador funcionando con el 100% de su carga y a velocidad nominal, en ese momento se desconecta súbitamente toda la carga con excitación constante, se debe medir la potencia en los bornes del generador al instante de la desconexión, se toma un registro gráfico de la frecuencia para determinar la variación de frecuencia en el tiempo y se espera a que la máquina acelera hasta un valor cercano al 1,07 de su velocidad nominal para regular la velocidad de nuevo y llevarla al reposo [3], como muestra la Fig. 12 el oscilograma de frecuencia que se obtiene.
Prueba de Perturbación a la Máquina Sincrónica
El circuito implementado en el laboratorio se representa mediante funciones de transferencia en el software MATLAB-Simulink como se muestra en la Fig. 13. La representación mediante funciones de transferencia de la máquina sincrónica permite analizar la perturbación aplicada y obtener una respuesta de la máquina sincrónica analizando la corriente de línea de la fase C, proveniente de un modelo genérico elegido para representar a la máquina sincrónica y cargado con los parámetros eléctricos encontrados con las pruebas de laboratorio.
RESULTADOS
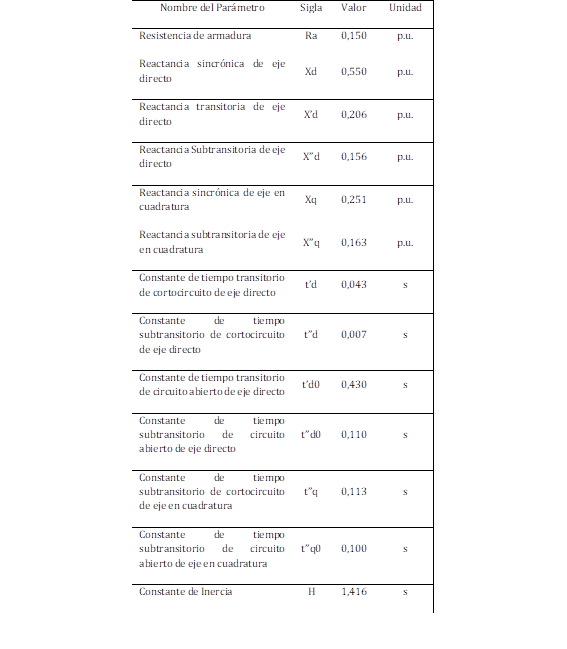
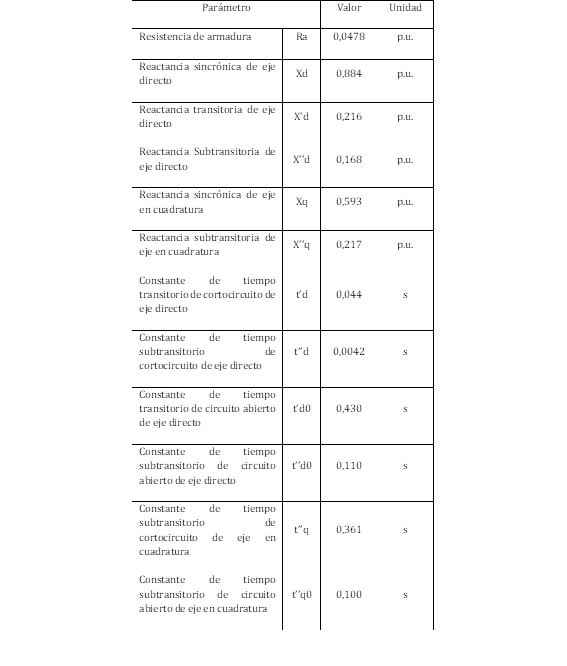
En esta sección se muestran los resultados de las pruebas realizadas en el laboratorio, luego de seguir la normativa IEEE Std 115, resumidos en la Tabla 3.
Estos parámetros no son confiables por las razones explicadas anteriormente, y por ello es necesario aplicar una metodología adicional en donde a la máquina se le aplica una perturbación sin carga luego de que el rotor este girando a velocidad nominal y entregando el voltaje nominal de armadura.
Perturbación del Voltaje de Campo
Para encontrar la respuesta experimental de la máquina sincrónica ante una perturbación se hace girar a la máquina a la velocidad sincrónica, y se le aplica un voltaje DC en la alimentación del campo. La perturbación seleccionada es una función paso, en forma de una variación de voltaje de larga duración. Se obtiene una variación de voltaje línea-línea de armadura como reacción de la perturbación aplicada.
En la Fig. 14 se observan los oscilogramas de entrada y de salida en voltaje vs tiempo, se ha elegido la función de voltaje de campo (Vf). El voltaje pico 52,2V es el ingresado como perturbación al circuito de campo de la máquina sincrónica, en este valor de voltaje se obtiene la corriente de campo nominal 1,2A y es utilizado para transformaciones a valores en p.u. de la onda ingresada como perturbación a la máquina sincrónica en la simulación.
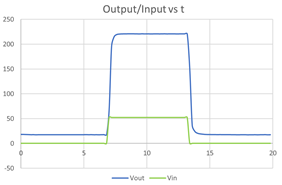
Figura 14: Oscilogramas de entrada y salida de la máquina en el laboratorio. Azul: Voltaje de armadura (salida). Verde: voltaje de campo (entrada).
Las respuestas de laboratorio y de simulación se deben superponer en un mismo gráfico para poder realizar el proceso de sintonización utilizando las herramientas de optimización en MATLAB-Simulink. Como se puede observar existe una gran similitud en las gráficas en la Fig. 15, se toma como referencia a la curva azul que es la respuesta de la máquina sincrónica en el laboratorio y la función a optimizar para sintonizar los parámetros eléctricos a la curva roja que es la respuesta del modelo estructurado en MATLAB-Simulink con los valores de los parámetros encontrados con la aplicación de la norma IEEE Std 115.
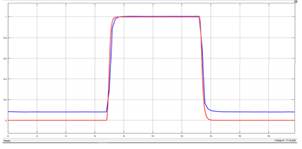
Figura 15: Superposición de respuestas. En azul señal medida en el laboratorio. En rojo señal obtenida en simulación.
Los resultados se obtienen cuando el método elegido Los resultados se obtienen cuando el método elegido converge cumpliendo con las tolerancias propuestas para la función de costo o error como se observa en la Fig.16, donde se cumple el objetivo de sintonizar los parámetros eléctricos de la máquina sincrónica, encontrados anteriormente con la aplicación de la norma IEEE Std 115 con el método de optimización “NONLINEAR LEAST SQUARES: LEVENBERG-MARQUARDT” y una tolerancia de 0.0000000001.
En las Tablas 4 y 5 se presentan los resultados de la estimación de los parámetros son los diferentes métodos de optimización utilizados.
En estas tablas se observa que el método Gradiente Descendente (GD) no maneja una exactitud adecuada para sintonizar los parámetros debido a que se ha ajustado a la función error con una tolerancia sumamente baja y los resultados siguen siendo los mismos.
Para el algoritmo de Punto Fijo active set (AS) el método no converge debido a que no cumple con las restricciones de límite donde lo parámetros no pueden valer cero o ser negativos, cuando la reactancia transitoria de eje directo Xpd y la reactancia subtransitoria de eje directo Xppd toman el valor de cero el método finaliza.
Para el algoritmo Trust Region Reflective (TRR) las condiciones que plantea la optimización con el modelo matemático de la máquina sincrónica no se adaptan a este método y por ello no los evalúa.
Del grupo de simulaciones del método Gradiente Descendente el mejor algoritmo es el de Interior Point (IP), aunque no es exacto tiene variaciones en todas las variables y la reducción en la función objetivo es la mayor de todos los algoritmos con un valor final de 0.467.
Los resultados del método Nonlinear Least Squares con el algoritmo (NLS) Levenberg-Marquardt (LM) y Trust Region Reflective (TRR), son prácticamente idénticos, por ello se asume los mismos resultados para ambos, y en próximas estimaciones se sugiere suprimir el uso de uno de estos dos métodos para comparación de resultados, y de acuerdo a la función objetivo, el método de menor error es Levenberg-Marquardt.
En el método Pattern Search los resultados se anulan inmediatamente debido a que los valores que alcanzan los parámetros son de hasta 192 p.u. como en el caso de la reactancia subtransitoria de eje directo Xppd.
El método Simplex Search también debe ser tomado en cuenta para posteriores simulaciones debido a que la exactitud que presenta es alta. Existe una diferencia visible en los resultados entre una tolerancia y otra. Pero la función objetivo es de 0,431 prácticamente para ambos casos y como se planteó en la sección 2.2.6, no respeta límites y aunque las respuestas a estos modelos no generan un valor negativo puede que en simulaciones posteriores si lo hagan.
Perturbación por un Cortocircuito Trifásico en los Bornes de la Armadura
Para realizar la sintonización de parámetros se utilizan los datos obtenidos en la prueba de cortocircuito trifásico súbito, se analiza la corriente de línea de la fase C como respuesta experimental para la herramienta computacional de optimización de parámetros en MATLAB-Simulink de la Fig. 17.
Tabla 5 Resultados de otros métodos de optimización.
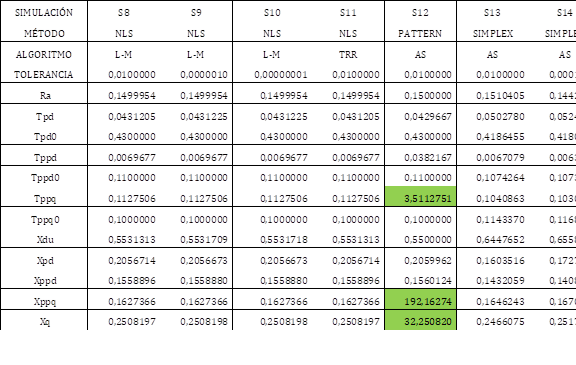
Donde, NLS, L-M, TRR, y AS, significan Nonlinear Least Squares, Levenberg-Marquardt, Trust Region Reflective y Active Set respectivamente
Herramienta de optimización en MATLAB-Simulink
Inicialmente los parámetros encontrados y cargados al modelo estructurado no reflejan el comportamiento de la máquina sincrónica, como se observa en la Fig. 18, pero son una aproximación que sirve como base de comparación para la utilización de la herramienta de optimización del software.
Como se observa con los mismos parámetros eléctricos que se manejaba anteriormente ahora se tiene mayores diferencias entre las curvas de respuesta experimental y de simulación, y se va a obtener mejores resultados ante estas respuestas generadas de una perturbación que describe de mejor manera a la máquina sincrónica.
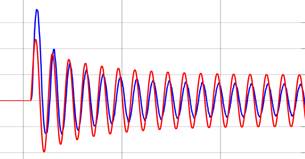
Figura 18: Resultado experimental=azul y simulación=rojo ante un evento de cortocircuito trifásico en bornes de armadura.
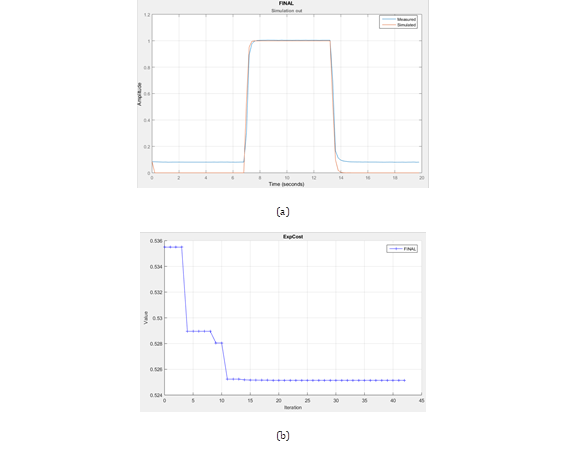
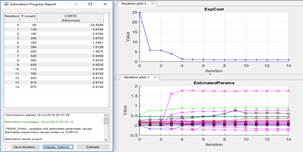
Se utiliza la herramienta de optimización “Parameter Estimation” de MATLAB-Simulink, y se configura su espacio de trabajo para mediante el algoritmo Levenberg-Marquardt, el método iterativo converge cumpliendo la menor tolerancia de 0.001, y muestra la variación de los parámetros en cada paso de iteración, como muestra la Fig. 19 donde el error entre las curvas inicialmente era 24.8588 y converge con un error de 0.9148.
Sintonización de parámetros con la oscilación de cortocircuito
En la Fig. 20 se observa el ajuste final de los oscilogramas experimentales y de simulación, en la pantalla del osciloscopio de MATLAB-Simulink dentro de la simulación del cortocircuito, con un error de la función optimizada (ajuste de las curvas) de 0.9148.
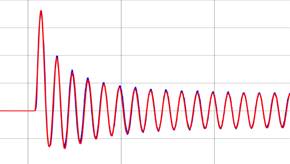
Figura 20: Respuesta grafica de la sintonización de parámetros utilizando MATLAB-Simulink. Resultado experimental=azul y simulación=rojo.
Como parámetros eléctricos sintonizados se tienen los valores finales de la simulación que alcanza valores cercanos a los valores iniciales de los parámetros eléctricos obtenidos en las pruebas del laboratorio, presentados en la Tabla 6.
Aunque los valores de la Tabla 6 son diferentes a la respuesta del oscilograma de voltaje rms evaluada anteriormente en las Tablas 4 y 5, se eligen estos nuevos parámetros encontrados como los parámetros sintonizados ya que se tienen mayores puntos de comparación y la oscilación de corriente de una falla trifásica intrínsecamente describe mejor el comportamiento de la máquina sincrónica.
Tabla 6: Parámetros eléctricos de la máquina sincrónica sintonizados con un cortocircuito trifásico.
CONCLUSIONES Y RECOMENDACIONES
El presente estudio proporciona un método válido para obtener los parámetros eléctricos de un generador sincrónico, donde determinación, inicia con la aplicación de la norma internacional IEEE Standard 115 - 2009. Con la finalidad de afinar los valores de estos parámetros, se captura la respuesta de la máquina ante una perturbación y simulando este ensayo en MATLAB-Simulink bajo las mismas condiciones de laboratorio, se obtiene la respuesta en simulación de la máquina ante la misma perturbación. Para finalizar se aplica la herramienta de optimización para sintonizar los parámetros eléctricos hacia el modelo de la máquina sincrónica seleccionada reduciendo los errores que puedan aparecer en todo el procedimiento y así entregar un modelo con parámetros eléctricos que reproducen a los efectos de la má
quina.
La elección de un modelo matemático que represente a la máquina sincrónica, que reproduzca sus condiciones de funcionamiento y maneje la mayoría de parámetros encontrados es de gran importancia para este estudio, para lo cual se eligió el modelo genérico de la librería de Simulink denominado como máquina sincrónica fundamental en p.u. basado en normativas IEEE. Este modelo cumple con los fundamentos matemáticos planteados de la máquina sincrónica, se adapta a las condiciones que se utilizaron en el ensayo de respuesta de la máquina ante una perturbación y maneja la mayoría de parámetros que se pueden encontrar con la aplicación de la norma IEEE Std 115.
La herramienta de optimización añade un valor agregado a este estudio, con su flexibilidad, maneja varios métodos iterativos de convergencia y aunque no todos se adaptan a las restricciones que deben tener los parámetros eléctricos se tiene varias opciones. Esta herramienta utiliza una función de costo o error en la cual se define la tolerancia, y en el transcurso de las iteraciones, su valor decrece hasta cumplir con el error planteado denominado como condición de paro o condición que se debe cumplir para la convergencia del método utilizado.
Para utilizar la herramienta de optimización en los parámetros eléctricos de la máquina es necesario que estas variables sean manejadas por un modelo estructurado en Simulink a base de funciones de transferencia, estas variables deben estar declaradas e inicializadas en el Workspace de MATLAB en este caso con un archivo .m. Es primordial tener dos respuestas gráficas, la primera se carga desde un archivo de Excel que en este caso es la respuesta de la máquina ante la perturbación en laboratorio y la segunda se adquiere mediante un puerto de señal a la salida del modelo estructurado en este caso a la salida de la máquina sincrónica simulada ante la misma perturbación.
Las simulaciones realizadas tienen la finalidad de entregar el mejor resultado el cual se obtiene con el método de Nonlinear Least Squares y con el algoritmo Levenberg-Marquardt encontrando la función error con menor valor y las curvas de respuesta experimental y de simulación sobrepuestas, que representan de mejor manera a los parámetros de la máquina sincrónica sintonizados.
Para encontrar los resultados de los parámetros eléctricos sintonizados, se realiza la simulación de un cortocircuito trifásico y se analiza la corriente de una línea, de igual menara se reproduce el evento en MATLAB-Simulink encontrando dos respuestas la experimental de laboratorio y la de simulación de MATLAB, adicional se utilizan los parámetros obtenidos en las pruebas del laboratorio y gracias a todos los análisis anteriores a esta sintonización se tiene el mejor método para utilizar la herramienta de optimización, de esta manera se ha elegido los parámetros sintonizados para la maquina sincrónica.
Aplicar este estudio a la base de datos del CENACE para el Sistema Eléctrico aportaría una mejora en los valores de los parámetros actuales, hay que señalar que las unidades de generación reales incluyen sistemas mucho más complejos y con mayores componentes, pero si se tiene los modelos estructurados en diagramas de bloque con sus parámetros, estos datos serían la primera aproximación para realizar la sintonización de los parámetros eléctricos en base a la metodología planteada. Adicionalmente, las unidades de generación reales acopladas al sistema cuando sufren una perturbación producen un oscilograma de respuesta, el cual puede ser simulado en base al modelo inicial, y con la herramienta de optimización se podría sintonizar los parámetros adecuadamente.
Las futuras aplicaciones de este estudio técnico estarán enfocadas en la determinación de los parámetros eléctricos de cualquier elemento constitutivo del sistema eléctrico que pueda ser representado por modelos matemáticos, como lo pueden ser transformadores, líneas de trasmisión, sistemas de control, sistemas de excitación de voltaje y velocidad. La condición indispensable es poder representar este elemento como una función de transferencia a la cual se le aplica una perturbación y el resultado de esta perturbación en la máquina sincrónica ayudará a obtener mediante los métodos de optimización los parámetros del modelo matemático correspondiente.