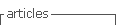Cómo citar:
Aguado-Franco, J. C. (2023). Aversión al riesgo, efecto certeza y estimación de probabilidades. Retos Revista de Ciencias de la Administración y Economía, 13(25), 49-60. https://doi.org/10.17163/ret.n25.2023.04
Introducción
La teoría de la utilidad esperada, desarrollada por Von Neumann y Morgenstern (1944), ha sido considerada durante décadas como el modelo normativo de elección racional en la toma de decisiones económicas en presencia de riesgo, asumiendo que el comportamiento de las personas respetaría sus axiomas. Así, según este modelo, la utilidad esperada que proporcionaría a un individuo el enfrentarse a una lotería se calcularía como la suma de las utilidades de los diferentes pagos, multiplicadas por sus respectivas probabilidades, de forma que el decisor optaría por aquella alternativa que tuviese una mayor utilidad esperada. Sin embargo, este planteamiento estaba cuestionado ya desde que se formuló la Paradoja de San Petersburgo (Bernouilli, 1738), traducida al inglés aquí: (Bernouilli, 1954), pues, entre otros motivos, ofrecía una enorme dificultad para valorar de forma razonable aquellas circunstancias en las que un determinado evento ofreciera un pago extremadamente alto que podía obtenerse con una probabilidad extremadamente pequeña.
Por otro lado, ante la reiterada evidencia encontrada en los procesos de toma de decisiones observados en numerosos estudios empíricos, en los que quienes tienen que llevarlos a cabo violan sistemáticamente los principios en los que se sustenta la teoría de la utilidad esperada, es fácil encontrar en la literatura especializada distintos modelos que se han desarrollado intentando de aproximarse más a la realidad de las decisiones adoptadas por los individuos (Machina, 1987; Camerer, 1989; Tversky y Kahneman, 1992). El modelo que ha tenido una mayor repercusión, pues explica las principales violaciones de la teoría de la utilidad esperada en contextos de elección con riesgo, es el de la teoría de las perspectivas (Kahneman y Tversky, 1979; Tversky y Kahneman, 1986; Tversky y Kahneman, 1992), hasta el punto de que el artículo de 1979 de ambos autores es el que recibe más citas en el ámbito de la economía y empresa (Merigó et al., 2016). La antes mencionada paradoja de San Petersburgo, de hecho, ha sido reconsiderada a la luz de la teoría de las perspectivas (Rieger y Wang, 2006).
La teoría de las perspectivas
La teoría de las perspectivas ha sido bien estudiada y revisada (Bendickson et al., 2017), y ha sido reconocida como la teoría descriptiva de la toma de decisiones ante el riesgo más relevante en la actualidad (Barberis, 2013; Starmer, 2000; Wakker, 2010), y a la que se le ha encontrado aplicación en muy variados ámbitos de toma de decisiones (Holmes et al., 2011), como en el análisis de las decisiones en los mercados inmobiliarios (Buisson, 2016), las apuestas (Bouchouicha y Vieiden, 2017), el sector de los seguros (Schmidt, 2016), la rentabilidad por dividendos de las acciones (Barberis et al., 2016), la toma de decisiones relativas al hecho de emigrar o permanecer viviendo en el mismo lugar (Morrison y Clark, 2016; Clark y Lisowski, 2017), decisiones acerca de si apostar o no en diferentes periodos, en un contexto dinámico (Ebert y Strack, 2015), decisiones acerca de qué cantidad de stock mantener de manera óptima, haciendo referencia al conocido “problema del vendedor de periódicos” (Long y Nasiry, 2015), los efectos de las leyes de bancarrota sobre las aspiraciones empresariales (Estrin et al., 2017), la cobertura de los seguros agrarios (Babcock, 2015), cuestiones relativas a la volatilidad de las inversiones y la baja rentabilidad (Bhootra y Hur, 2015), decisiones acerca de llevar a cabo acciones de carácter militar (Niv-Solomon, 2016), las relaciones internacionales entre los países (Feng y He, 2017; Stein, 2017), la asunción de riesgos por parte de los políticos (Linde y Vis, 2017), decisiones que se toman en el marco del deporte, en concreto en el fútbol americano (Bendickson et al., 2017), la predicción de resultados deportivos (Pérez-Martínez y Rodríguez-Fernández, 2022), la optimización de carteras (Grishina et al., 2017), entre otros.
A diferencia de lo que sucede en la teoría de la utilidad esperada, en la que la aversión o el amor al riesgo están determinados únicamente por la función de utilidad del individuo, en la teoría de las perspectivas entran en juego una serie de factores adicionales que afectan a su proceso de toma de decisiones, más allá de aspectos individuales como la personalidad de los decisores (Chávez-Santana et al., 2021; López et al., 2023) y otras variables psicológicas que también tienen su influencia en ámbitos de toma de decisiones, como la teoría de juegos (López et al., 2022). En efecto, en la teoría de las perspectivas, la función de utilidad sería cóncava respecto al punto de referencia en el caso de las ganancias, mientras que sería convexa respecto a ese mismo punto en el caso de incurrir en pérdidas. De esta forma, tanto en el caso de las ganancias como en el de las pérdidas, el impacto de cualquier cambio es menor cuanto más alejados nos encontremos del punto de referencia inicial (existe una sensibilidad decreciente ante los efectos de una determinada variación monetaria experimentada).
Por otra parte, según este modelo, la pendiente de la función sería mayor en el caso de las pérdidas que en el de las ganancias, reflejado de esta manera la existencia de una aversión a las pérdidas, por la que se observa una asimetría que se plasma en que una pérdida de una determinada cantidad de dinero tiene un mayor impacto sobre el nivel de utilidad del individuo que una ganancia equivalente. Finalmente, son las ganancias o las pérdidas monetarias que se experimentan las que son consideradas para calcular la utilidad, y no la situación final en la que se encuentran los individuos cuando obtienen estas ganancias o pérdidas, como ocurre en la teoría de la utilidad esperada (Tversky y Kahnemann, 1991).
La paradoja de Allais y el efecto certeza
La ausencia de linealidad en las preferencias que se recoge en los enunciados de Kahneman y Tversky fue puesta de manifiesto hace ya bastantes décadas, a mediados del siglo pasado. En efecto, Allais (1953) mostró empíricamente en un congreso científico que la diferencia entre probabilidades de un 99 % y un 100 % tiene un impacto más elevado en las preferencias de los individuos que la diferencia entre un 10 % y un 11 %, por ejemplo.
Kahneman y Tversky (1979), en la misma línea de las conclusiones extraídas por Maurice Allais, afirmaron que los decisores tienen tendencia a infravalorar los pagos que son meramente probables, en comparación con aquellos que se obtienen con certeza, hecho este que denominaron el “efecto certeza”. Esta tendencia contribuye a la aparición de comportamientos que muestren aversión al riesgo en elecciones en las que haya la posibilidad de obtener un pago seguro, mientras que provocaría amor por el riesgo en aquellas otras situaciones en las que existan posibilidades de pérdidas seguras.
El problema que Kahneman (2011) utiliza para ilustrar de forma simplificada las disyuntivas que le sirven para explicar la paradoja de Allais se podría representar de la manera siguiente:
Ante estas dos situaciones representadas, en las que hay que elegir entre la alternativa A y la B en la primera ocasión, y entre C y D en la segunda, la mayoría de las personas eligen la lotería de 520 000 en la primera disyuntiva (ganar 520 000 con una probabilidad 0,61, frente a ganar 500 000 con una probabilidad 0,63), mientras que optan por la alternativa D en la disyuntiva de la parte inferior (eligiendo ganar 500 000 con certeza antes de ganar 520 000 con probabilidad 0,98). De esta forma, se está vulnerando la teoría de la utilidad, dado que el incremento de probabilidad de 0,37 que se produce en las alternativas de la parte inferior, con respecto a las de la parte superior, favorecería más a la alternativa C que a la D, pues aumenta la posibilidad en el primer caso de obtener 520 000, y en el segundo caso incrementa la probabilidad de obtener 500 000. Se incurre por tanto en un “efecto certeza”, según el cual a los resultados que se obtienen casi con certeza se les da un valor menor del que justificaría su probabilidad.
Si se hubiese utilizado el criterio de la maximización del valor esperado monetario de cada alternativa, se habría tenido que calcularlos y compararlos:
Si se hubiese utilizado el criterio de la maximización del valor esperado monetario de cada alternativa, se habría tenido que calcularlos y compararlos:
VEM(A) = 520000 x 0,61 + 0 x 0,39 = 317200
VEM(B) = 500000 x 0,63 + 0 x 0,37 = 315000
VEM(C) = 520000 x 0,98 + 0 x 0,02 = 509600
VEM(D) = 500000
De forma que VEM(A) > VEM(B) y VEM(C) > VEM(D)
El decisor debería, en ese caso, elegir la alternativa A y la alternativa C frente a B y D, respectivamente. Sin embargo, no existe interés en comparar las ganancias esperadas de las distintas alternativas, sino en la utilidad que dichas ganancias proporcionan al individuo.
En efecto, utilizando las funciones de utilidad Von Neuman-Morgenstern, suponiendo que un individuo prefiera en el primer problema de decisión la primera opción a la segunda, se tiene:
0,61 x u(520) > 0,63 x u(500)
Por otro lado, en el caso de una función de utilidad monótonamente creciente, resulta evidente que:
0,37 x u(520) ≥ 0,37 x u(500)
Sumando a ambos lados de la desigualdad anterior, se debería cumplir que:
0,98 x u(520) > 1 x u(500)
Dicho de otro modo; si un decisor elije A frente a B, debería elegir C frente a D.
En otras palabras, la opción C debería elegirse ante la opción D, independientemente de si el decisor muestra aversión o amor por el riesgo. Alguien que elija las opciones A y D estaría incumpliendo los principios de la utilidad esperada; no existe una función de utilidad compatible con ambas decisiones. Se trataría, por tanto, de una decisión irracional. De hecho, Daniel Kahneman reconoce que uno de los primeros objetivos que se propuso cuando comenzó a trabajar con Amos Tversky fue hallar una adecuada explicación psicológica de por qué se produce la paradoja de Allais (Kahneman, 2011), y hasta el día de hoy se siguen utilizando distintas versiones de la paradoja de Allais para estudiar y analizar las tomas de decisiones de los individuos en situaciones de riesgo (Berlinger, 2015; Bruhin et al., 2022).
Como afirma Thaler (2016), cuando las personas realizan elecciones entre distintas alternativas, lo hacen basándose en un conjunto de expectativas acerca de las consecuencias de sus decisiones, así como de muy variados factores exógenos que pueden determinar cómo evolucionarán todas esas variables en el futuro. Además, tradicionalmente, los economistas asumían que tales creencias estaban libres de sesgos, hecho que no es compartido de manera general en la actualidad, como se puede observar en la literatura existente parte de la cual ha sido citada en el epígrafe anterior.
En efecto, como señalan Slovic y Tversky (1974), ante la observación y la constatación empírica de la violación de los axiomas de la teoría de la decisión racional, muchos teóricos de la decisión consideraban que esos hechos deberían ser tratados como errores de juicio debidos a descuidos, a la ausencia de incentivos adecuados, o simplemente por errores de comprensión de los problemas planteados. Sin embargo, la existencia de numerosos heurísticos y sesgos cognitivos en el comportamiento de los individuos a la hora de tomar decisiones económicas en entornos de riesgo o incertidumbre ha sido profusamente estudiada, y los aportes desde la psicología económica o la economía conductual, analizando la existencia de efectos marco, efectos dotación, efecto anclaje, efecto posibilidad, efecto certeza, etc. que han venido a enriquecer el conocimiento de cómo se produce dicho proceso de toma de decisiones y de qué factores afectan a ese comportamiento.
Por otra parte, existen estudios empíricos muy recientes que demuestran que las preferencias de los individuos no vienen dadas de forma inamovible, sino que se construyen sobre la marcha, influenciadas por el contexto de toma de decisiones, y su experiencia reciente en ese ámbito (Kusev et al., 2020, 2022). En este estudio, ahondando en esa línea, se introducirá una consideración que de manera general no ha sido contemplada en la literatura existente, y que consiste en encontrar la relación que pueda existir entre el nivel de comprensión que tienen los individuos acerca de la probabilidad de que se presente un determinado suceso, con la postura ante el riesgo que presenten estos individuos, en situaciones propicias para la aparición del efecto certeza.
En efecto, el conocimiento matemático básico de las probabilidades, que se suele dar por sentado en los estudios precedentes, parece ser relevante cuando alguien se enfrenta a un problema de decisión, en el que puede obtener diferentes resultados en función de determinados sucesos que pueden ocurrir con una determinada probabilidad, de forma que el desconocimiento de esos principios básicos de las probabilidades podría influir de alguna manera en sus decisiones. De esta forma, aun siendo conscientes de que existen muchas variables diferentes que influyen en la toma de decisiones de los individuos, el objetivo es comprender mejor las razones que conducen a actitudes diferentes hacia el riesgo, introduciendo esta nueva variable, que es el conocimiento básico o el desconocimiento de las probabilidades de que ocurra un determinado suceso.
Metodología
En el marco de la XXVI Jornada Internacional de Investigación de la Universidad Pedagógica y Tecnológica de Colombia, se realizó un estudio experimental en el que se planteó un problema de decisión a los asistentes, de la misma forma que hizo Maurice Allais en París en un encuentro para discutir sobre economía del riesgo al que asistieron economistas como Samuelson, Arrow, Friedman o el estadístico Jimmie Savage. El problema se planteó tanto a quienes asistieron de forma presencial como a quienes lo siguieron a distancia con medios virtuales, de forma que se minimizaba el posible sesgo que pudiera aparecer como consecuencia de que se comunicaran unos participantes con otros al responder a las preguntas. Se obtuvieron 149 respuestas al formulario diseñado al efecto, en el que no se solicitaba ningún dato que permitiera conocer la identidad de las personas, con el fin de que pudieran contestar libremente y con absoluta confidencialidad.
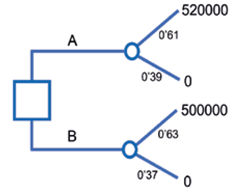
En el formulario que rellenaron, tras ver la representación gráfica del problema de la figura 1, los participantes debían elegir entre la alternativa A y la B en función de sus preferencias, alternativas con las que hipotéticamente podían obtener unos pagos conforme al siguiente enunciado:
Imagine que se enfrentara usted a un juego como el de la imagen. Si opta por la alternativa A, ganará 520 000 con una probabilidad 0’61, y no ganará nada con una probabilidad 0’39. Si por el contrario opta por la alternativa B, ganará usted 500 000 con una probabilidad 0’63 y no ganará nada con una probabilidad 0’37. Indique a continuación cuál de las alternativas elegiría usted.
Con objeto de conocer el grado de comprensión que tenían los participantes en el estudio acerca de las probabilidades ante sucesos aleatorios, se les planteó el siguiente enunciado:
Imagine que de una bolsa que contiene 50 bolas rojas y 50 bolas blancas se extrae aleatoriamente una. Se apunta de qué color es, se vuelve a introducir en la bolsa, y se repite el proceso, así hasta 7 veces. Indique cuál de las siguientes secuencias considera usted más probable que salga.
Las secuencias a las que hace referencia el enunciado son las de la figura 2.
Las posibles respuestas que se ofrecían en el formulario, en consonancia con las secuencias reproducidas en la imagen, fueron las siguientes:
roja, roja, roja, roja, roja, roja, roja
blanca, blanca, blanca, blanca, blanca, blanca, blanca
roja, blanca, roja, blanca, roja, blanca, roja
roja, roja, blanca, roja, blanca, blanca, roja
todas las secuencias anteriores tienen la misma probabilidad
La respuesta correcta es la última, ya que todas las secuencias tienen la misma probabilidad (1/128).
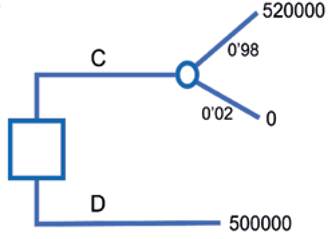
Después, los participantes en el estudio debían responder cuál sería su elección cuando se modificaban las probabilidades de obtener los pagos del problema de decisión inicial, conforme al problema representado en la figura 3, y que respondía al siguiente enunciado:
Imagine que se enfrentara usted a un juego como el de la imagen. Si opta por la alternativa A, ganará 520 000 con una probabilidad 0’98, y no ganará nada con una probabilidad 0’02. Si por el contrario opta por la alternativa B, ganará usted 500 000 con certeza. Indique a continuación cuál de las alternativas elegiría usted.
El problema que se examina, al considerar las respuestas dadas a ambos problemas de decisión, responde al planteamiento de la “paradoja de Allais”, y pretende mostrar la inconsistencia que muestran algunos individuos en la toma de decisiones, lo que los lleva a incumplir la teoría de la utilidad esperada.
En efecto, una persona que eligiera la alternativa A en el primer problema, “debería” hacerlo también en el segundo. Esto es así porque, en el segundo problema, se ha incrementado en la alternativa A en un 37 % la probabilidad de obtener un pago de 520 000 frente al problema inicial, mientras que en la alternativa B se ha incrementado en un 37 % la probabilidad de obtener un pago de 500 000.
La ganancia esperada de la alternativa A ha crecido, por tanto, en 192 400, mientras que la ganancia esperada de la alternativa B ha aumentado solamente en 185 000; si en el primer problema se eligió la alternativa A, con mayor motivo se debe hacer lo mismo en el segundo problema si se actuara con “racionalidad económica”.
Resultados
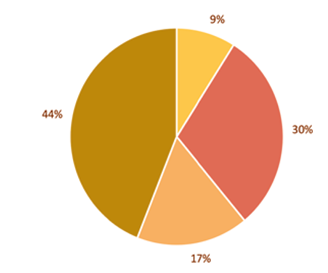
El 30 % de los participantes en el estudio (véase figura 4) incurrieron en esa situación consistente en subestimar los resultados que son meramente probables en comparación con los resultados que se obtienen con certeza, respondiendo A y D ante los dos problemas de decisión planteados.
Las otras tres posibles combinaciones de respuestas que se obtuvieron son las siguientes:
AC (9 %) son personas que se ven atraídas por la posibilidad de obtener el mayor pago, el de 520 000, y son consistentes en sus elecciones, en el sentido de que eligiendo A en el primer problema, lo hacen también en el segundo.
BC (17 %) son personas que muestran en el primer enunciado aversión al riesgo, pues eligen la alternativa que tiene menor ganancia esperada, pero en la que la probabilidad de no ganar nada es menor. Sin embargo, estas personas se ven atraídas por la probabilidad muy cercana a 1 de obtener el mayor pago (520 000) en el segundo problema. Se podría interpretar que inicialmente ambas alternativas estaban cercanas en la valoración del individuo, con ligera ventaja para la alternativa B, pero que la mejora experimentada en el pago de la alternativa A al pasar a C, que es mayor que la experimentada por pasar de B a D, ha desnivelado la balanza a favor de la primera opción.
BD (44 %) son personas que muestran aversión al riesgo en ambos problemas, optando siempre por aquella alternativa en la que la probabilidad de obtener un pago es mayor.
Con respecto a la pregunta que buscaba conocer hasta qué punto los participantes en el estudio tenían un conocimiento básico de las probabilidades, solo el 50,34 % de las respuestas emitidas fueron correctas, distribuyéndose los fallos casi por igual entre quienes opinaban que lo más probable era que se alternaran los colores (rojo, blanco, rojo, blanco, rojo, etc.) y quienes consideraban más probable la secuencia “rojo, rojo, blanco, rojo, blanco, blanco, rojo”. La explicación a que las respuestas de un porcentaje tan elevado de personas fueran ambas respuestas erróneas no es difícil de encontrar.
En el primer caso, porque como el color de cada bola extraída puede ser rojo o blanco con idéntica probabilidad, ante el hecho de que en una ocasión salga uno de los dos colores, por ejemplo el rojo, las personas pueden pensar que la siguiente bola extraída “debería” ser blanca, y por tanto la siguiente roja, y la siguiente blanca, y así sucesivamente, sin darse cuenta de que se trata de sucesos independientes y ser un ejercicio de extracción con reemplazamiento, por lo que en cada etapa la probabilidad de ambos colores es idéntica e igual a 0,5. En el segundo, porque el hecho de que sea una secuencia que no responde a ninguna pauta concreta que pueda ser reconocida fácilmente, las personas pueden suponer que tiene más probabilidades de ocurrir que el resto, en las que sí que se puede apreciar una ordenación clara. Eso es un error, pues esa secuencia determinada en concreto tiene la misma probabilidad de ocurrir que el que sean todas las bolas de un color concreto o se alternen sucesivamente uno y otro color, por ejemplo.
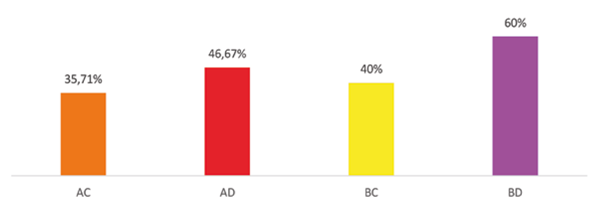
Ahora bien, la pregunta de análisis que se plantea dado estos datos es: ¿existe alguna relación entre las personas que responden correctamente (o erróneamente) a la pregunta de las bolas rojas y blancas, y las respuestas dadas en el problema de la paradoja de Allais? Para analizarlo, se ha elaborado un gráfico que recoge el porcentaje de personas que responde correctamente en la pregunta de las bolas rojas y blancas, relacionándolo con las respuestas dadas en el problema de la paradoja de Allais. Así, antes de relacionar estos resultados con los obtenidos en el problema de decisión, ya se aprecia una notable diferencia de respuestas correctas a favor de quienes contestaron BD, con un 60 %, muy superior especialmente a quienes respondieron AC (35,71 %) y BC (40 %).
Conclusiones y discusión
A lo largo de la historia se ha estudiado la forma en que los individuos toman decisiones económicas cuando se encuentran ante problemas de elección entre distintas alternativas, en las que los resultados que puedan obtener dependen de diversas circunstancias, a las que se puede dar una probabilidad de presentarse. El criterio de la maximización del valor esperado monetario, que consiste en elegir aquella alternativa cuya ganancia esperada sea mayor tras hacer una suma ponderada de los distintos pagos por sus correspondientes probabilidades, fue superado en el momento en el que se consideró la postura ante el riesgo con las funciones de utilidad (Von Neuman-Morgenstern, 1944).
Sin embargo, siguieron apreciándose situaciones en las que los decisores incumplían de forma sistemática los principios de la teoría de la utilidad. Así, existe un amplio consenso en admitir que el hecho de alterar la forma de presentar los problemas (por ejemplo, en términos de ganancias o de pérdidas), conlleva sistemáticamente a la expresión de preferencias diferentes; es lo que se ha llamado el “efecto marco”. Del mismo modo, aunque en el análisis económico de las decisiones en entornos de riesgo e incertidumbre se asume generalmente la existencia de aversión al riesgo, hay circunstancias en las que los decisores muestran amor por el riesgo. Esto ocurre, por ejemplo, cuando se compra lotería. En la lotería se tiene una ínfima probabilidad de obtener un premio muy elevado, pero si se calcula el valor esperado monetario de la lotería, sumando todos los posibles pagos, multiplicados por la probabilidad de obtener cada uno de ellos (incluida la posibilidad de no ganar absolutamente nada) se tiene, obviamente, un resultado que es muy inferior al precio que se paga. También se observó amor por el riesgo, cuando existe obligación por elegir entre sufrir una pérdida segura y obtener una pérdida aún mayor, no segura, pero que se puede producir con una alta probabilidad. La posibilidad de poder evitar esa pérdida, aunque sea con una probabilidad muy pequeña, puede resultar atractiva si la comparamos con la alternativa de tener una pérdida con certeza.
La existencia de preferencias no lineales, como demostró Allais (1953) y se ha explicado en este artículo, es otra de las circunstancias en las que se producen inconsistencias en el comportamiento de los individuos en los procesos de toma de decisiones económicas, llevándolos a actuar de forma que se podría calificar de “irracional” conforme a los postulados de la teoría de la utilidad. La existencia de un efecto certeza, que Allais sugirió y que tiene explicación en la teoría de las perspectivas que desarrollaron Kahneman y Tversky (1992), está detrás de esa irracionalidad.
En casi todos los párrafos anteriores, en este apartado de conclusiones y discusión, se han mencionado, como un factor fundamental para la toma de decisiones, las probabilidades de que ocurran los distintos sucesos. Así, se asume que el hecho de que los resultados que se puedan obtener, como consecuencia de las decisiones que se toman entre distintas alternativas, estén condicionados por dichas probabilidades, esto, conlleva un cierto conocimiento acerca de las probabilidades, no ya de las que afecten al problema abordado, sino del concepto de probabilidad en general. En caso contrario, las irracionalidades mencionadas contarían con una fuente adicional basada en el desconocimiento o la confusión.
Analizando los datos aportados en el apartado de resultados, se pudo observar que el grupo de personas que realizaron las elecciones en las que mostraban verse afectadas por el efecto certeza de una manera más clara, es decir, quienes respondieron alternativa A y alternativa D sucesivamente ante los dos problemas de decisión que se les plantearon, tienen un porcentaje de acierto en la pregunta correspondiente a la probabilidad (la de las bolas rojas y blancas) que es muy cercano a la media: 46’67 frente al 49’66. Con los datos de este estudio, por tanto, no se puede concluir que haya ninguna relación entre ambos hechos. Sin embargo, resulta llamativo el porcentaje de personas (60 %) que optaron por las alternativas B y D en los problemas de la paradoja de Allais (optando por aquellas loterías en las que tenían una mayor probabilidad de ganar, aun cuando el pago fuera menor que el ofrecido por la otra alternativa, mostrando, por tanto, aversión al riesgo) y que a la vez respondieron acertadamente a la pregunta relativa a la estimación de probabilidades, (indicando que todas las secuencias presentadas tenían la misma probabilidad de ocurrir). En efecto, ese porcentaje es un 50 % mayor que el de quienes respondieron B y C a las dos preguntas, y casi un 70 % mayor que quienes optaron por la opción A en la primera pregunta y C en la segunda.
A falta de más estudios que lo corroboren, con muestras mayores y considerando factores adicionales, de los datos de este trabajo se puede concluir que existe una relación positiva entre comprender adecuadamente las probabilidades de que sucedan determinados sucesos, con el hecho de mostrar un mayor nivel de aversión al riesgo. Visto en sentido contrario, cuanto menor sea el conocimiento que posean de cómo funcionan las probabilidades, más probable es que los individuos tomen decisiones arriesgadas, en las que puedan obtener pérdidas que en ocasiones pueden ser muy elevadas. En cualquier ámbito de toma de decisiones (administración pública, administración privada empresarial o particulares), es necesario comprender cuáles son los factores que afectan a las personas cuando se enfrentan a situaciones de decisión con riesgo o incertidumbre, pues de ello dependerán en parte sus resultados. Este estudio señala la conveniencia de reforzar el estudio matemático de las probabilidades para que los ciudadanos sean capaces de tomar decisiones económicas (de inversión, por ejemplo) que no se vean penalizadas por el hecho de incurrir en riesgos elevados como consecuencia de un conocimiento limitado de la teoría de la probabilidad.