1. INTRODUCCIÓN
En los últimos años el Sistema Nacional Interconectado del país ha tenido un crecimiento notorio debido al aumento de la población y a la necesidad de mejorar el servicio. En este progreso los transformadores juegan un papel muy importante: elevar y reducir el voltaje para transportar la energía eléctrica. Por esto, es esencial que funcionen de manera óptima (Tibanlombo & Granda, 2018). Para verificar su funcionamiento y calidad se realizan pruebas en su fábrica antes de su puesta en servicio; de igual manera este equipo debe protegerse ante eventualidades internas y externas al sistema eléctrico, por tal motivo, se deben realizar pruebas que aseguren su protección. Para tener información y poder coordinar sus protecciones se deben realizar pruebas para obtener los parámetros que ayuden a realizar ciertos ajustes para su protección (Reyes Ruiz, 2012).
Para determinar ciertos parámetros, entre estos, los de secuencia positiva, negativa y cero, se deben realizar pruebas según los estándares internacionales ANSI, IEEE e IEC, los cuales proponen aspectos generales para tomar en cuenta durante la medición de secuencias con el fin de no exceder corrientes, voltajes o límites térmicos en el transformador (Reyes Ruiz, 2012), (IEC, 2011), (IEEE, 2015). Estos parámetros en los equipos de protección asociados a los transformadores en un sistema eléctrico requieren de modelos para su simulación, tanto del transformador como de la red eléctrica en la que está instalado. Sin embargo, si el modelo del transformador no es el adecuado, entonces la simulación no va a ser correcta y, por lo tanto, el ajuste de las protecciones tampoco va a ser adecuado
En el modelo de las componentes simétricas desarrollado por C. L. Fortescue se establecen las condiciones para el cálculo de las fallas trifásicas, bifásicas, bifásicas a tierra y monofásicas, éstas dos últimas poseen componentes de secuencia cero, por lo que su cálculo es de mucha importancia (Sorrentino & Burgos, 2012).
En los eventos de fallas monofásicas y bifásicas a tierra, el problema se da debido a la influencia de la impedancia de secuencia cero, este valor se presenta en equipos con conexión estrella principalmente, ya que estos tienen un conductor de neutro que normalmente está sólidamente aterrizado (Angela Ramos, Burgos, Moreno, & Sorrentino, 2013).
También se debe a la forma y construcción del transformador, pues las paredes del tanque del transformador proporcionan un camino para una parte del flujo magnético de secuencia cero (Sorrentino & Burgos, 2012).
Sin embargo, varios transformadores en servicio, en su placa de características no incluyen datos de secuencia cero que permitan un análisis preciso de su comportamiento bajo cargas desequilibradas y fallas.
Con lo antes expuesto, las pruebas en el laboratorio siguen las metodologías de cálculo que se indican en las normas internacionales para la obtención de sus parámetros; sin embargo, existe una diferencia de valores entre lo medido y lo simulado. Para evidenciar esto, se realiza una comparación de las corrientes obtenidas en la simulación con respecto a las medidas en la parte experimental aplicando un evento de cortocircuito en los terminales del transformador (Angel Ramos & Burgos, 2017).
Si los valores de corriente resultan ser muy diferentes, significa que los parámetros del modelo del transformador no se asemejan a la realidad, una razón es debida a las limitaciones físicas para elaborar estas pruebas en laboratorio. Con esta problemática se propone un método práctico para reducir esta diferencia de corriente a la salida de los bornes de un transformador trifásico de 50 kVA en el lado de bajo voltaje, comparando la corriente del modelo estructurado en el software MATLAB-Simulink con la corriente del modelo real obtenido en las pruebas normalizadas en el laboratorio (Chiguano, Valenzuela, & Gallardo, 2018), (Chiguano, Ramírez, Quilumba, & Gallardo, 2018).
Para solucionar esta problemática, se plantea evaluar el desempeño del transformador trifásico ante un evento de cortocircuito experimentalmente en el laboratorio y su comparación con el del modelo simulado realizando el mismo evento. La diferencia que se obtenga de las dos respuestas se reducirá utilizando los métodos de optimización para la estimación de parámetros con las que cuenta la herramienta MATLAB-Simulink.
2. PRUEBAS NORMALIZADAS PARA DETERMINAR LOS PARÁMETROS DE SECUENCIA EN UN TRANSFORMADOR TRIFÁSICO
2.1 Prueba de Circuito Abierto
Esta prueba se realiza con el fin de determinar la corriente de magnetización y las pérdidas de hierro en el núcleo del transformador en función del voltaje aplicado. Generalmente se alimenta al transformador por el lado de bajo voltaje y se mantienen los terminales del lado de alto voltaje abiertos, los equipos de medida se colocan en el lado de la alimentación a voltaje nominal. Al encontrarse los terminales abiertos en una rama del transformador, la fuente genera una potencia que se disipa en el núcleo en forma de calor, por esta razón la corriente de magnetización es muy pequeña por lo que se desprecia la resistencia del devanado (IEEE, 2015).
Las mediciones que se realizan son: voltaje de alimentación, corriente de magnetización y potencias. Los métodos de ensayo a detalle se pueden encontrar en los dos estándares de (IEC, 2011), (IEEE, 2015). Los parámetros que se pueden obtener de este ensayo son la reactancia de magnetización XM y la resistencia de magnetización del núcleo RM.
2.2 Prueba de Cortocircuito
Esta prueba se realiza con el fin de determinar las pérdidas en los devanados, para esto, los terminales de alto voltaje se alimentan con una fuente regulable hasta que circule la corriente nominal del lado de bajo voltaje con sus terminales en cortocircuito. Las mediciones de voltaje, corriente y potencia deberán realizarse cuando estén conectados sus devanados en el tap principal. En el lado de alto voltaje, el voltaje se reduce entre el 4-10% del voltaje nominal, expresado en porcentaje (IEEE, 2015).
Las pérdidas en el núcleo del transformador son despreciables al igual que el flujo en el núcleo, esto se debe a que una fracción del voltaje nominal pasa por el lado de alto voltaje. Estas mediciones se las debe hacer de manera conjunta y mediante cálculos se puede separar valores para determinar los parámetros de los devanados de corto circuito en el lado de bajo voltaje. Los métodos de ensayo a detalle se pueden encontrar en (IEC, 2011), (IEEE, 2015).
Se deben tomar las mediciones del voltaje de cortocircuito Vccl, corriente de cortocircuito Iccl, potencias de cortocircuito Pccl, Qccl. Los parámetros que se pueden obtener de este ensayo son: la resistencia de secuencia positiva R1 y reactancia de secuencia positiva X1 de ambos bobinados del transformador.
2.3 Prueba de Secuencia Cero
En los transformadores eléctricos es preciso conocer la impedancia de secuencia cero para estudios con diversos fenómenos en redes de potencia trifásica en condiciones de desequilibrio. En una red eléctrica con carga simétrica, solamente aparecen las impedancias positiva y negativa; sin embargo, ante una perturbación asimétrica, la magnitud de las corrientes de cortocircuito o sobretensiones en fallas monofásicas y bifásicas a tierra en estado estacionario está influenciada por la impedancia de secuencia cero en su gran parte (IEC, 2011).
Para el transformador u otro elemento no rotativo de la red eléctrica las impedancias positiva y negativa son iguales razón por la cual hay que poner atención a la impedancia de secuencia cero. Por otra parte, el transformador dependiendo del tipo de conexión, construcción del núcleo en cuanto a su posición de sus devanados y a su circuito magnético va a tener diferentes características de impedancia se secuencia cero (IEC, 2011).
La impedancia de secuencia cero de un transformador se expresa en ohmios/fase a la frecuencia de la red y se obtiene conectando en paralelo las 3 bobinas de un transformador en estrella (Y) y su terminal neutro (IEC, 2011).
Para que exista un valor de impedancia cero diferente de infinito en un transformador trifásico al menos uno de sus arrollamientos debe tener una conexión en estrella o zigzag. De igual manera es preciso que la red tenga neutro para que existan corrientes de secuencia cero. Los métodos de ensayo a detalle se pueden encontrar en los dos estándares de (IEC, 2011).
El cálculo de la impedancia de secuencia cero Z0 se presenta en la Ecuación (1).
Donde:
V = Voltaje aplicado fase neutro.
I = Corriente de prueba del neutro.
La impedancia de secuencia cero consta de dos componentes: resistiva
Se debe tener en cuenta que el flujo de secuencia cero puede causar un calentamiento excesivo en las partes estructurales metálicas del transformador bajo prueba como el tanque, tapa y elementos de sujeción. Por este motivo la corriente de medición no debe ser superior al 30% de la corriente nominal. La inyección de corriente nominal solo se permite por un tiempo muy corto (unos pocos segundos) y el voltaje aplicado no debe exceder el voltaje de fase a neutro que se produce durante el funcionamiento normal (Carlson & Zürich, 2003).
3. METODOLOGIA
3.1 Falla Monofásica a Tierra en los Transformadores Bajo Prueba
Para la obtención de los parámetros estimados del modelo del transformador en estudio se realizan las siguientes acciones:
Se conocen unos parámetros iniciales del transformador obtenidos a través de ensayos normalizados en el laboratorio según lo indicado en las secciones 2.1, 2.2 y 2.3 de este artículo.
Se genera un cortocircuito controlado monofásico a tierra y bifásico a tierra en el laboratorio y se adquieren las señales de corriente de las fases cortocircuitadas mediante un osciloscopio para ser utilizadas digitalmente.
Se realiza en Simulink una simulación de los mismos eventos de cortocircuito del punto 2) utilizando un modelo del transformador en el que se pueden ingresar los parámetros obtenidos en el punto 1).
4) Se comparan los resultados de las curvas de corriente de cortocircuito medidas y simuladas y se utiliza la herramienta Parameter Estimation de Simulink para realizar un ajuste de las curvas, de manera que, los parámetros del modelo cambian para lograr que las curvas simuladas sean muy similares a las curvas medidas. Este es el proceso de estimación de los parámetros.
5) Una vez que se obtienen los nuevos parámetros en el proceso de estimación se cuantifica la diferencia de las curvas ajustadas por medio del error cuadrático medio RMSE y también se comparan los errores relativos de los parámetros iniciales y los nuevos parámetros. Combinando estos dos errores se determinan finalmente los parámetros del modelo.
3.2 Problema de optimización
La herramienta Parameter Estimation de Simulink formula la estimación de parámetros como un problema de optimización y la solución del problema de optimización es un conjunto de valores de los parámetros seleccionados (MathWorks, 2019).
El problema de optimización consiste de: las variables de diseño que en este problema son los parámetros del modelo y sus estados iniciales; la función objetivo, función de costo o estimación del error calcula una medida de la diferencia entre las respuestas medidas y simuladas del modelo; los límites entre los que pueden variar los parámetros del modelo; las funciones de restricción si existiesen restricciones en las variables de diseño (MathWorks, 2019a).
Al resolver el problema la herramienta estima los valores de las variables de diseño para satisfacer los objetivos y restricciones especificados. La formulación exacta del problema de optimización depende del método que se desee utilizar. Los métodos disponibles en la herramienta son: Mínimos Cuadrados No Lineales, Gradiente Descendente, Búsqueda Simple y Patrones Búsqueda; con los algoritmos de Levenberg-Marquadt, Conjunto Activo, Punto Interior, Región de Confianza Reflexiva, Programación Cuadrática Secuencial (SQP). La utilización detallada de estos métodos puede encontrarse en (Chiguano et al., 2018).
4. CASOS DE ESTUDIO
Las pruebas se realizaron en un transformador didáctico del Laboratorio de Máquinas Eléctricas de la Escuela Politécnica Nacional para determinar las impedancias de secuencia (Z+, Z-, Z0). Para obtener las curvas de cortocircuito se realizarán dos eventos de fallas, una monofásica a tierra y una bifásica a tierra. En esta primera parte se realizan todas estas pruebas en el transformador trifásico didáctico con conexión Dyn5 debido a que el transformador de 50 kVA que se usará posteriormente tiene internamente esta conexión; para obtener los valores iniciales de sus parámetros y validar el modelo estructurado en MATLAB-Simulink. Por último, se realizará la estimación de los parámetros de secuencia.
En segundo lugar, se realiza el mismo procedimiento, pero en el transformador de 50 kVA. Se realizan las pruebas para determinar las impedancias de secuencia (Z+, Z-, Z0). En la realización de los eventos de fallas cuando se trabaja con el transformador de 50 kVA se alimenta al transformador por el lado de alto voltaje a 500 V debido a las condiciones físicas del Laboratorio de Máquinas Eléctricas que no dispone de un voltaje de 6300 V para alimentarle. Por último, se realizará la estimación de los parámetros de secuencia.
Debido a que las simulaciones de los cortocircuitos en Simulink requieren del valor de la resistencia de puesta a tierra, se midió la resistencia de puesta de tierra del Laboratorio de Máquinas Eléctricas, utilizando el método del 62% dado por la norma IEEE 80-2013 (IEEE, 2013).
4.1 Transformador Trifásico Didáctico
El transformador tiene sus tres devanados de cada fase en un solo núcleo ferromagnético con bobinas de 120 V a 5 A. Esta máquina se encuentra en el Laboratorio de Máquinas Eléctricas de la Escuela Politécnica Nacional, se le realiza una conexión Dyn5.
4.2 Transformador Trifásico de 50 kVA
El transformador en el que se aplicará la metodología para determinar los parámetros de secuencia (Z+, Z-, Z0) tiene internamente una conexión Dyn5, razón por la cual se realizó la misma conexión en el transformador didáctico. En los eventos de falla, se alimentará a un voltaje reducido de 500 V y no al voltaje que necesita de 6300 V por disposición física en el Laboratorio de Máquinas Eléctricas, donde se realizarán estos eventos. Los datos de placa de este equipo se encuentran en la Tabla 1.
4.3 Falla Monofásica a Tierra en los Transformadores Bajo Prueba
La falla monofásica a tierra es una de las fallas asimétricas (causadas por líneas que caen a tierra, por cadena de aisladores que se rompen debido a las cargas de hielo, por daños permanentes en las torres y por fallas de los apartarrayos) que más ocurren en el sistema, es la falla que con más frecuencia se presenta. El 70% y 80% de las fallas ocasionadas en el sistema son fallas monofásicas a tierra (MukeshThakre & Mishra, 2013).
Una vez realizada la conexión Dyn5 y alimentado por el lado de alto voltaje con una fuente variable trifásica, se procederá a conectar en el lado de bajo voltaje una de las tres fases libres a tierra.
En el caso del transformador trifásico didáctico, para generar el evento de cortocircuito se utiliza un interruptor bipolar de 25 A – 125 V; en el cual, al momento de cerrarse generará un cortocircuito monofásico a tierra.
Para tomar la información se procede a capturar rápidamente la curva de corriente de cortocircuito con la ayuda del osciloscopio digital en la fase a tierra como se aprecia en la Figura 1a. Se coloca una resistencia de muy bajo valor entre la fase que va a tierra del lado de bajo voltaje y el interruptor bipolar para medir el valor de corriente en forma de voltaje con el osciloscopio.
Para la realización del evento de cortocircuito en el transformador trifásico de 50 kVA, se alimenta con una fuente regulable de 500 V trifásica por el lado de alto voltaje. Para su protección en el lado de alto voltaje se colocan fusibles en cada fase que soportan una corriente de hasta 5 A.
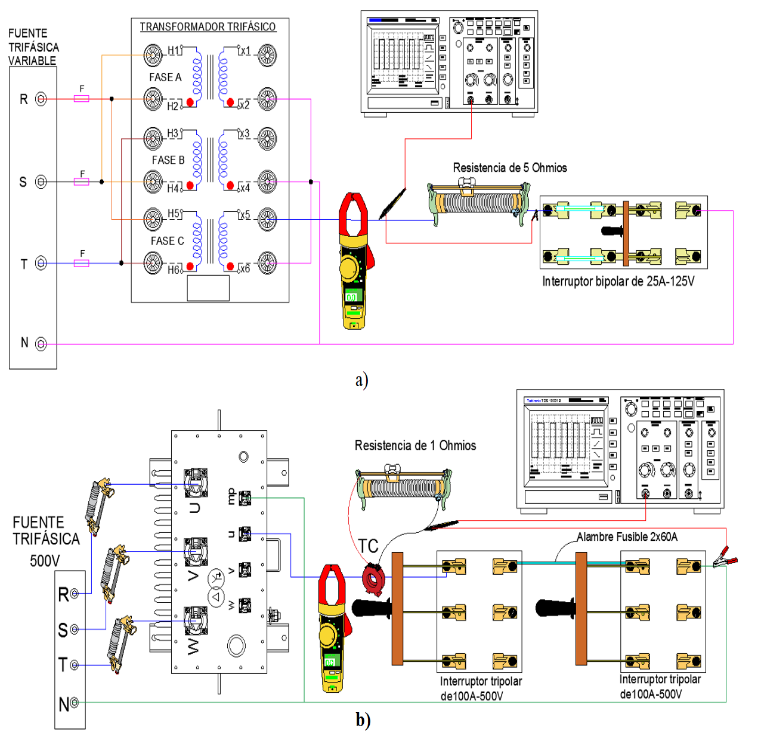
Figura 1. a) Conexión del transformador trifásico didáctico para el evento de falla monofásica a tierra. b) Conexión del transformador trifásico de 50 kVA para el evento de falla monofásica a tierra
En el lado de bajo voltaje se conecta una de las tres fases a tierra para luego tomar las mediciones de la corriente de cortocircuito. Para generar el evento de cortocircuito se utiliza un interruptor tripolar de 100 A – 500 V, al momento de cerrar las cuchillas, la medición a tomar se realiza rápidamente para no causar esfuerzos significativos al transformador y la fuente de energía; con ayuda del osciloscopio y la pinza amperimétrica como se aprecia en la Figura 1b.
Para la protección en el lado de bajo voltaje se coloca un fusible que soporta 120 A en cada fase a tierra, para esto se coloca en paralelo alambre fusible de 60 A. En cada una de las fases se coloca un transformador de corriente (TC) para reducir su valor y registrar los datos de corriente de cortocircuito en el osciloscopio.
4.4 Falla Bifásica a Tierra en los Transformadores Bajo Prueba
La falla bifásica se debe a que dos de las fases se vinculan con la tierra. Esta prueba es muy similar al del evento de falla monofásico, con la diferencia de que se conectan ahora dos fases del lado de bajo voltaje del transformador a tierra.
4.5 Modelo del Transformador Trifásico Seleccionado
En esta parte se presenta el modelo a utilizar del transformador trifásico. Se utiliza el modelo “Three-Phase Transformer (Two-Windings)” que se encuentra en la biblioteca de MATLAB-Simulink en la sección Specialized Power Systems /Fundamental blocks/ Elements. El modelo del transformador trifásico a utilizar cumple con los siguientes requisitos:
Los parámetros poseen la capacidad de ajustarse a los valores calculados en las pruebas de laboratorio.
Posee la capacidad de manejar los parámetros que se ingresan al modelo como variables para realizar la estimación de parámetros utilizados los métodos de optimización con la herramienta de Matlab Parameter Estimation.
Tiene la capacidad de realizar los mismos eventos que se realizan en el laboratorio.
Este es un modelo que tiene una sustentación teórica y que se ha venido desarrollando con normas internacionales y que aún se encuentran activas en la biblioteca de Matlab R2019a.
El bloque está constituido por tres transformadores monofásicos. Los devanados se pueden conectar con la notación estándar de bobinas, la primera letra corresponde al bobinado de alto voltaje ya sea este en estrella o delta (Y o D) y con letra minúscula en el bobinado de bajo voltaje (y o d) en estrella o delta. Si se selecciona Y con neutro en cualquiera de las bobinas, aparecerá un puerto N (MathWorks, 2019b).
Se selecciona Three-limb core (core-type) para trabajar con un transformador trifásico de tres ramas, tipo núcleo. Este tipo de modelo produce resultados precisos durante un evento de falla asimétrica. Durante las condiciones de voltaje asimétrico, el flujo de secuencia cero de un transformador tipo núcleo retorna por fuera del núcleo a través del aire, el acero de la estructura del transformador y de su tanque. Así, la inductancia de secuencia cero natural L0 de un transformador de tipo núcleo es generalmente muy baja
En primera instancia se debe escoger las unidades en las que se desea trabajar, en este trabajo se utilizan los valores en por unidad para evitar que los resultados en las simulaciones se vean reflejado desde la bobina 1 o la bobina 2. La potencia que se debe trabajar será la nominal con una frecuencia de 60 Hz. Para los bobinados 1 y 2 se debe ingresar el voltaje rms, el valor de las resistencias e inductancias calculadas de las pruebas de laboratorio, tanto para el lado de alto voltaje como para el lado de bajo voltaje.
Para la parte de magnetización se debe ingresar los valores RM y LM, valores que son calculados de las pruebas de laboratorio. Para la inductancia L0 solo existe esa opción ya que la resistencia de secuencia cero es muy pequeña comparada a su parte inductiva y este valor se obtiene de las pruebas de laboratorio.
4.6 Estimación de Parámetros
Se desarrolla en MATLAB una rutina donde se ingresan los valores de los parámetros iniciales que se obtienen después de realizar las pruebas de laboratorio en los transformadores. Adicionalmente, reconoce la información que se registra en el osciloscopio de los eventos de las fallas monofásicas y bifásicas a tierra en formato de Excel donde se puede generar las curvas de corriente de cortocircuito.
En Simulink se estructura mediante bloques la simulación de un transformador trifásico con la conexión deseada, donde también se puede realizar los eventos de cortocircuitos monofásicos y bifásicos a tierra. Este archivo también reconoce los valores de corriente de cortocircuito que fueron registrados de la parte experimental en el osciloscopio con el objetivo de superponer las curvas reales y simuladas. Este modelo se aprecia en la Figura 2.
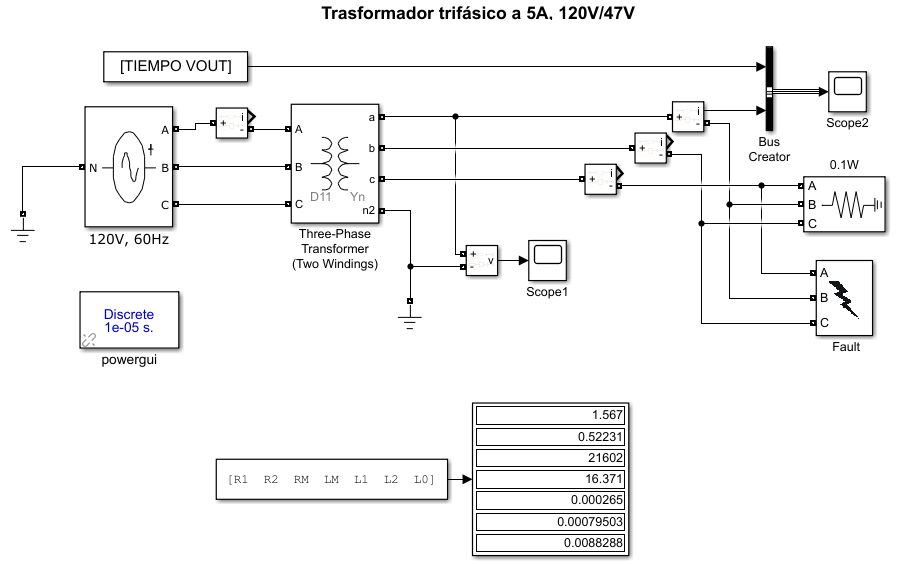
Figura 2. Estructuración del programa para la optimización de parámetros de secuencia en un transformador trifásico
Al correr este programa se generarán dos curvas; la simulada y la real medida en el laboratorio. Para la estimación de los parámetros de secuencia se utilizarán métodos de optimización no lineal de los que dispone la herramienta como son: Levenberg-Marquadt, Gradiente Descendente, Región de Confianza Reflexiva, Conjunto Activo, Punto Interior, Programación Cuadrática Secuencial (SQP), Patrón de Búsqueda y Búsqueda Simple.
La utilización de estos algoritmos se realiza con la herramienta Parameter Estimation de Simulink que hace que los parámetros del modelo varíen hasta un valor donde las curvas reales y simuladas de corrientes de cortocircuitos queden lo más parecidas posibles.
5. RESULTADOS Y DISCUSIÓN
5.1 Parámetros de Secuencia
En la Tabla 2 se presentan de los valores iniciales de los parámetros calculados con las pruebas de laboratorio para trabajar en las simulaciones de MATLAB-Simulink.
Tabla 2. Valores Iniciales en p.u. de los Parámetros de Secuencia de los Dos Transformadores en Estudio
|
Valores en p.u. para trabajar en el modelo | ||
|
Parámetros |
Transformador Didáctico |
Transformador de 50 kVA |
|
R1 |
0,065243 |
0,011174 |
|
R2 |
0,065243 |
0,011174 |
|
RM |
299,75 |
499,007 |
|
LM |
85,637 |
47,1318 |
|
L1 |
0,012449 |
0,016175 |
|
L2 |
0,012449 |
0,016175 |
|
L0 |
0,000123 |
0,041204 |
5.2 Resultados de los Cortocircuitos en los Transformadores Trifásicos Didáctico y de 50 kVA con Conexión Dyn5
Una vez realizado el cortocircuito cuando se cierran las cuchillas del interruptor bipolar, el osciloscopio registra los datos de la forma de onda en archivos .CSV que luego son tratados en Excel.
5.3 Estimación de Parámetros
5.3.1 Transformador Didáctico
En el transcurso de las simulaciones en los transformadores bajo prueba, se determinó que el método “Gradiente Descendente” con el algoritmo “Región de Confianza reflexiva” y el método “Patrón de Búsqueda” no convergen en ninguna circunstancia debido a que estos no respetan los limites inferiores y no encuentran el punto óptimo para ir iterando para mejorar su función objetivo. Con estos dos métodos la herramienta de MATLAB-Simulink para optimizar indica un aviso de alerta de que no puede converger.
En el proceso de la estimación de parámetros en el transformador didáctico se utilizaron todos los métodos de optimización Levenberg-Marquadt, Gradiente Descendente, Conjunto Activo, Punto Interior, Región de Confianza Reflexiva, Programación Cuadrática Secuencial (SQP), Patrón de Búsqueda y Búsqueda Simple.
Para este proceso se comparan las formas de onda de corriente de cortocircuito del lado de bajo voltaje del transformador trifásico bajo prueba con la curva de corriente que resulta del modelo estructurado en MATLAB-Simulink. Los tiempos donde inicia el cortocircuito deben ser iguales tanto del modelo en MATLAB como de la parte medida en el laboratorio.
Posteriormente la estimación logra que la curva del modelo se asemeje a la curva real variando los parámetros del modelo. Al realizar las iteraciones e ir ajustando las dos formas de onda, la función objetivo que utiliza este método se va reduciendo hasta un valor que sea el óptimo durante todo el proceso. Una vez que se comprueba con el transformador didáctico que la estimación de parámetros es posible y exitosa se procede de manear similar con el transformador de interés de 50 kVA.
5.3.2 Transformador Trifásico de 50 kVA
En la Figura 3 se presenta un ejemplo de la corriente de cortocircuito monofásico en la fase A. Una curva es el resultado de la simulación del modelo utilizado en Simulink y la otra es la medida en el laboratorio. Se parecía la diferencia entre las dos debido a que los parámetros del transformador no corresponden precisamente a la realidad. En la Figura 4 se presentan las mismas curvas luego de haber realizado un proceso de estimación de parámetros y se puede apreciar que la corriente simulada se aproxima de mejor manera a la corriente medida.
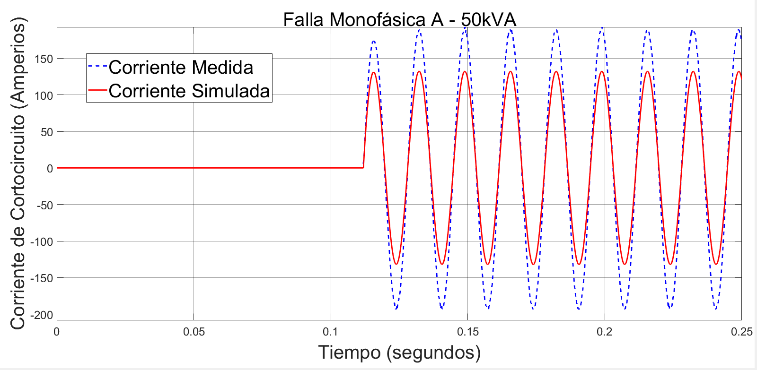
Figura 3. Curvas de corriente de falla monofásica en la fase A. Roja: del modelo de Simulink. Azul: medida. Antes del proceso de estimación de parámetros.
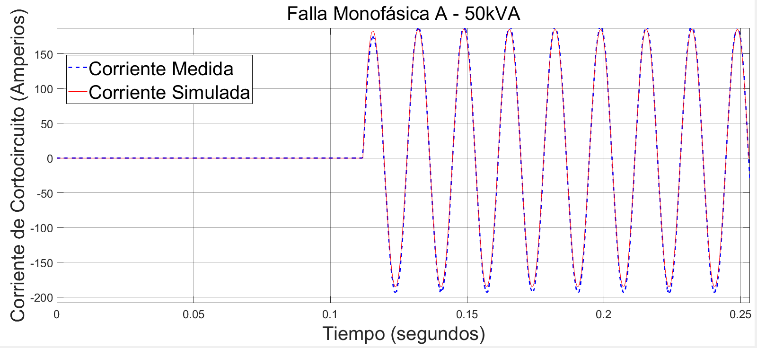
Figura 4. Curvas de corriente de falla monofásica en la fase A. Roja: del modelo de Simulink. Azul: medida. Luego del proceso de estimación de parámetros.
Tabla 3. Errores RMSE Antes y Después de la Estimación con los Métodos Utilizados
|
Error RMSE antes de la estimación |
Error RMSE después de la estimación |
||||
|
Método: |
Falla Monofásica a tierra fase |
Falla Bifásica a tierra fases |
Falla Monofásica a tierra fase |
Falla Bifásica a tierra fases |
|
|
A |
AB |
A |
AB |
||
|
Levenberg-Marquadt |
2,496 |
3,645 |
0,721 |
0,9310 |
|
|
Región de Confianza Reflexiva |
2,496 |
3,597 |
0,721 |
0,9306 |
|
|
Conjunto Activo |
2,495 |
3,551 |
0,721 |
0,9306 |
|
|
Punto Interior |
2,807 |
3,614 |
0,721 |
0,9306 |
|
|
Programación Cuadrática Secuencial |
2,812 |
3,654 |
0,721 |
0,9306 |
|
|
Búsqueda Simple |
2,761 |
3,554 |
0,721 |
0,9306 |
|
En la Tabla 3 se observan los errores RMSE antes y después de la estimación utilizando todos los métodos de optimización dando como resultado valores menores lo que indica que las curvas están muy cerca entre sí.
Luego se calculó el promedio de los parámetros resultantes de los diferentes métodos de optimización, se determina un valor promedio total de todas las fallas y se presentan los parámetros finales en la Tabla 4 donde el error relativo entre los parámetros iniciales y estimados presenta la diferencia que se ajustó con este procedimiento.
Tabla 4. Resultados Promedios de los Parámetros de Secuencia del Transformador de 50 kVA
|
Parámetro |
Promedio |
Valor inicial |
Error relativo % |
|
R1 |
0,009984977 |
0,011174 |
10,64 |
|
R2 |
0,011512888 |
0,011174 |
3,03 |
|
RM |
502,5718512 |
499,007 |
0,71 |
|
LM |
45,92161765 |
47,1318 |
2,57 |
|
L2 |
0,015803562 |
0,016175 |
2,30 |
|
L1 |
0,016909791 |
0,016175 |
4,54 |
|
L0 |
0,054105219 |
0,041204 |
31,31 |
El mejor método de estimación fue Levenberg-Marquadt. Con el método de punto interior, los parámetros RM y LM se elevan demasiado con respecto a los valores iniciales y los únicos que no varían tanto son R1 y L1, es decir los de secuencia positiva, por lo que no se recomienda utilizar este método.
Para una mejor comprobación del modelo, se ha realizado en el programa computacional PowerFactory una simulación de un transformador trifásico de 50 kVA de las mismas características y efectuando los mismos eventos de fallas, monofásicas a tierra y bifásicas a tierra.
Los parámetros ingresados en este transformador son los que resultaron de las estimaciones de parámetros en MATLAB de la Tabla 4, y resultan curvas muy parecidas a la del modelo de Simulink y a la corriente medida como se presenta en la Figura 5.
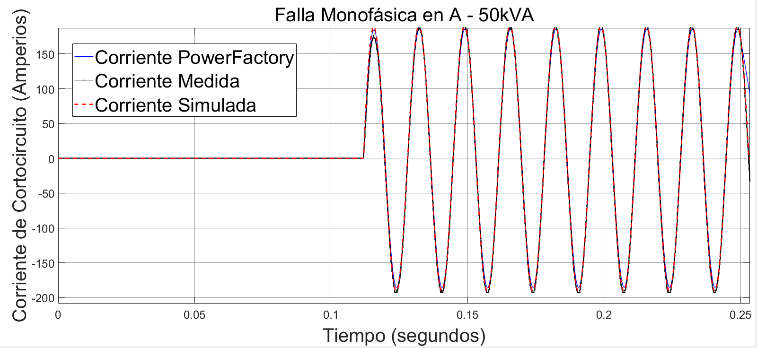
Figura 5. Curvas de corriente de falla monofásica en la fase A. Roja: del modelo de Simulink. Azul: modelo de PowerFactory. Negra: medida. Luego del proceso de estimación de parámetros.
No hay mayor diferencia entre las curvas de la Figura 5, lo que significa que bajo las mismas condiciones de falla e iguales características del transformador trifásico de 50 kVA el modelo se asemeja mucho a la realidad. En la Tabla 5 se presentan los errores RMSE entre las curvas de la Figura 5.
Tabla 5. Errores RMSE entre las Curvas Simuladas y la Medida.
|
Curvas comparadas |
RMSE |
||
|
Corriente medida |
vs. |
Corriente simulada en Simulink |
2.8773 |
|
Corriente medida |
vs. |
Corriente simulada en PowerFactory |
4.453 |
|
Corriente simulada en PowerFactory |
vs. |
Corriente simulada en Simulink |
2.515 |
Como resultado final se obtiene la validación de los parámetros dados en la Tabla 5 como los valores de los parámetros aceptables para el transformador de 50 kVA en estudio dentro del margen de error de la estimación.
6. CONCLUSIONES
Se realizó la estimación de los parámetros de secuencia de un transformador trifásico mediante la utilización de la herramienta Parameter Estimation de MATLAB-Simulink. Esta herramienta contiene diferentes métodos de optimización no lineal con lo cual se logra ajustar las curvas producidas por los eventos de fallas en el transformador trifásico de 50 kVA simuladas con respecto a las medidas.
En los resultados analizados se observa que todos los métodos reducen el error RMSE, pero este valor no es el único que se impone para decidir cuál es el mejor método para estimar los parámetros. En las tablas de resultados también se analiza el error relativo y en algunos métodos puede ser muy grande; esto significa que muchos parámetros diferentes pueden producir la misma curva y por esta razón no necesariamente son los valores reales. Debido a esto se requiere analizar tanto el error RMSE y el error relativo.
El modelo presentado puede tomar medidas de un transitorio de corriente de un transformador trifásico y estimar sus parámetros sin conocer los parámetros iniciales; sin embargo, en este proyecto sí se conocen estos valores y con ello se puede correr varias simulaciones y permite determinar cuál es el mejor de los métodos.
Para escoger el mejor método hay que combinar el que realice el ajuste lo mejor posible por medio del menor RMSE y por medio del menor error relativo de los parámetros de partida el cual fue en este proyecto el de Levenberg-Marquadt.