Introducción
Los avances científicos de los UAVs en los campos de la detección (Nevalainen et al. 2017), las comunicaciones (Amorim et al. 2017), los sistemas de control (Yongqiang et al. 2009), etc., han dado lugar a una explotación constante de la tecnología actual. En particular, el mercado mundial de los UAVs se encuentra en plena expansión, hasta el punto de que en la actualidad existen varias previsiones y proyecciones dentro del mercado de los UAV. En específico, en el Sistema Nacional de Espacio Aéreo en Estados Unidos se prevé un impacto económico de la integración de los UAVs, y un crecimiento sustancial que alcanzará más de 82,1 mil millones de dólares entre 2015 y 2025 (Valavanis y Vachtsevanos 2015).
Durante décadas, el desarrollo de los UAVs ha tenido como objetivo sustituir a los pilotos humanos en diversas misiones. Las diferentes tecnologías de los UAVs están en constante evolución, por lo que su desarrollo tecnológico no se ha detenido, independientemente de las soluciones que se presenten sobre determinados problemas. Así, incluso cuando se han completado soluciones a problemas concretos, dichas soluciones han sido objeto de nuevos cambios y modificaciones, lo que demuestra que la resolución sobre las diferentes problemáticas presentes en la temática UAV continúa en estado abierto y de ahí la necesidad de un desarrollo más profundo.
La tarea de planificación de trayectorias y evasión de obstáculos en un espacio euclídeo 3D, ha sido abordada desde diversos paradigmas metodológicos, ya sean empíricos o heurísticos. Estas diversas metodologías parten de una base de muestreo continuo o discreto (Aguilar y Morales 2016; Yao, Wang, y Su 2015), algoritmos basados en nodos (Dijkstra 1959; Hart & Nils 1968; Nosrati, Hasanvand, & Original 2012; Verscheure et al. 2010), algoritmos bioinspirados (Gautam & Verma 2014; Goel et al. 2018; Iswanto, Wahyunggoro, & Cahyadi 2016), entre otras técnicas (Wang, Chu, y Mirjalili 2016; YongBo et al. 2017). Metodologías desarrolladas sobre entornos: con o sin obstáculos (estáticos o dinámicos), por lo tanto, presentan ventajas y desventajas (Szirmay-Kalos & Márton 1998). Por otro lado, es importante destacar que, la teoría de la complejidad y análisis de algoritmos (AofA) involucrada en esta diversidad de metodologías conlleva una alta carga computacional O 𝑛 log 𝑛 (Chivers et al. 2015) como se puede ver en la Tabla 1.
Tabla 1: Costo computacional y complejidad en la estructura del grafo, 𝑛 es el número de vértices y 𝑚 es el número de aristas.
| Método | Tiempo de Complejidad | Memoria | Tiempo Real |
|---|---|---|---|
| Algoritmos de muestreo | 𝑂 𝑛 log 𝑛 𝑂 𝑛 2On-line | ||
| Algoritmos basados en nodos | 𝑂 𝑚 log 𝑛 𝑂 𝑛 2On-line | ||
| Algoritmos bioinspirados | 𝑂 𝑛 log 𝑛 𝑂 𝑛 2On-line |
En concreto, este trabajo se enfoca en la determinación de trayectorias en entornos 3D, mediante muestreo discreto. En este sentido, se ha tomado como punto de partida la metodología de descomposición adaptativa de celdas (ACD), puesto que presenta sólidas características que resuelven sistemas físicos dominados por ecuaciones diferenciales parciales (Berger & Oliger 1984). Es importante destacar que, esta técnica ofrece una sustancial mejora en tiempo computacional, además que la discretización no se rige por un sistema de ecuaciones dominante. De la misma forma, la ACD se utiliza en reconstrucciones cartesiana 3D (Hasbestan & Senocak 2018). No obstante, el enfoque presentado en este trabajo no intenta realizar una reconstrucción refinada del entorno, se centra en la determinación de los espacios ocupados y espacios libres dentro del espacio cartesiano 3D. Por tanto, se busca alcanzar un ahorro de esfuerzo computacional y de memoria, tomando una estructura computacional por medio de un etiquetado rápido de la figura geométrica del entorno como un sólido 3D de forma rectangular.
Gran parte de la literatura en el campo de la planificación de trayectorias se centra en la optimización de la distancia. Partiendo de este hecho, este trabajo busca incluir no sólo la distancia como parámetro principal en la generación de una trayectoria 3D, sino que también se pueden incluir otras características, que influyan tanto en el desplazamiento (geométricas del entorno), como posibles restricciones de vuelo (velocidad, capacidad de giro, batería, entre otros); entonces, el objetivo es alcanzar una trayectoria 3D que tenga en cuenta todas las restricciones posibles en un tiempo de cálculo mínimo, como se ha definido en la sección 2, donde se detallan diferentes restricciones de vuelo. Por tanto, el lector puede agregar características y condiciones adicionales para la generación de una trayectoria 3D, partiendo de sus requerimientos geométricos y restricciones de vuelo.
Es importante señalar que la tarea de planificación de trayectorias implica completar dos subtareas fundamentales dentro del espacio de trabajo 𝕎. Estas tareas implican posición y orientación, entendiéndose como posición 𝑝 𝑥,𝑦,𝑧 y orientación 𝑜 𝜑,𝜓,𝜃 . Entonces, el objetivo es alcanzar otra posición y orientación definidas dentro de 𝕎 , ya sea individualmente o ambas a la vez. En este sentido, se destaca que el procedimiento descrito a continuación, completa la tarea de planificación de trayectorias en posición, para lo cual se definen un punto inicial 𝑞 𝑖 = 𝑥 𝑖 , 𝑦 𝑖 , ?? 𝑖 y un punto meta 𝑞 𝑔 = 𝑥 𝑔 , 𝑦 𝑔 , 𝑧 𝑔 (la orientación será tratada en un próximo trabajo, a través de curvas suaves, siendo ejemplos relevantes de estudio los trabajos planteados por (Armesto, Vanegas, & Girbés-Juan 2022; Girbés, Vanegas, & Armesto 2019; Vanegas et al. 2018, 2022).
Entonces, si se asume las características completas del 𝕎 . Así, como las dimensiones 3D 𝑋,𝑌,𝑍 del 𝕎, los obstáculos (dimensiones y ubicaciones) dentro del 𝕎 , el punto de partida 𝑞 𝑖 del UAV, y el punto de meta 𝑞 𝑔 . Entonces, el objetivo es realizar una descomposición discreta (parcial y recursiva) del 𝕎, con el fin de determinar el conjunto finito de octantes contiguos y libres de colisiones que unen 𝑞 𝑖 con 𝑞 𝑔 . La trayectoria final genera un vector de puntos 3D 𝜌 𝑘 = 𝑥 𝑘 , 𝑦 𝑘 , 𝑧 𝑘 con 𝑘=1,…,𝑛 , siendo 𝑛 el número total de puntos del vector.
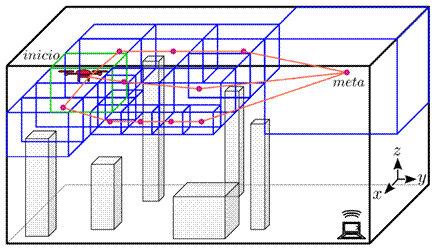
La Figura 1 muestra un ejemplo de un entorno urbano con edificios de varias dimensiones en distintas ubicaciones. El entorno se somete a una descomposición discreta, que da lugar a espacios libres de colisiones en forma de octantes 3D (color azul). Esto significa que, en función de las características del obstáculo, puede determinarse la trayectoria de escape alrededor de los obstáculos (hacia arriba, hacia abajo, hacia la izquierda o hacia la derecha). Por lo tanto, el UAV puede evitar los obstáculos realizando maniobras 3D verticales y/o horizontales.
Se muestran varias trayectorias posibles (líneas rosas) desde la ubicación actual del UAV y el punto objetivo. Los puntos magenta indican el número de puntos necesarios para construir la trayectoria. Los octantes azules muestran espacios libres de colisiones. El octante verde indica la posición actual del UAV.
Este trabajo se organiza de la siguiente forma: En la Sección 2, se explica el nuevo algoritmo de planificación de trayectorias 3D. En la Sección 3 se describen ejemplos de experimentos y sus resultados. La sección 4 expone una breve discusión de los resultados. Finalmente, las conclusiones y trabajos futuros se consideran en la sección 5.
Metodología
Para completar el problema de planificación de trayectorias 3D, a continuación, se describe la metodología desarrollada en este trabajo. Entonces, partiendo de la definición de las condiciones iniciales (características espaciales de 𝕎, dimensiones y ubicaciones de los obstáculos 𝑂 , estados inicial 𝑞 𝑖 y final 𝑞 𝑔 ), se determina cada posible estado futuro del sistema, donde, cada estado actual se define como un octante 𝑆 𝑓𝑟𝑒𝑒 y el conjunto de posibles estados futuros se define como el conjunto de octantes vecinos 𝑆 𝑓𝑟𝑒𝑒 . Por lo tanto, se asume Γ como un espacio de trabajo discreto 3D, que contiene un conjunto finito de octantes libres de colisiones 𝑆 𝑓𝑟𝑒𝑒 y un conjunto finito de octantes ocupados ?? 𝑜𝑐𝑐𝑢𝑝 .
Si se asume que el UAV está incluido dentro de la localización inicial, que a su vez se considera como el estado inicial 𝑠 𝑘 , el objetivo es alcanzar el punto objetivo 𝑞 𝑔 . Entonces, se asume un conjunto formado por octantes de diferentes tamaños 𝑆 𝑘+1 como vecindad de 𝑆 𝑘 . En este contexto, se puede desarrollar un modelo de estado y una matriz de transición, donde se determina la transición óptima de 𝑆 𝑘 a cualquier estado perteneciente a 𝑆 ??+1 basándose en dos medidas de transición ( 𝐷 1 y 𝐷 2 ). Por lo tanto, partiendo del estado actual 𝑠 𝑘 , el método intenta obtener el estado vecino óptimo perteneciente a 𝑆 𝑘+1 𝑠 𝑘 → 𝑆 𝑘+1 = 𝐷 1 . A continuación, se localiza la sub-trayectoria desde cada vecino de 𝑆 𝑘+1 hasta el punto final 𝑞 𝑔 , siendo la mejor 𝑆 𝑘+1 → 𝑞 𝑔 = 𝐷 2 .
Para resolver este problema se ha definido un autómata finito determinista discreto (DDFA) (Skoldstam, Akesson, y Fabian 2007), siendo 𝐹=(𝑆,𝐺,𝐷,𝑞 ) 𝑇 un conjunto de funciones parciales 𝑅 𝑚 , donde, los parámetros 𝑞 son dos puntos en el espacio del entorno 3D, mientras que 𝑞 𝑖 representa el punto inicial, y 𝑞 𝑔 representa el punto final. Por otra parte, 𝑆 define el conjunto finito de 𝑀 estados actuales, para lo que 𝑆 𝑓𝑟𝑒𝑒 define el conjunto finito de octantes libres de colisión, divididos en el octante actual 𝑠 ?? = 𝑠 𝑘 𝑥 , 𝑠 𝑘 𝑦 , 𝑠 𝑘 y el conjunto de sus vecinos 𝑠 𝑘+1 = 𝑠 𝑘+1 𝑥 , 𝑠 𝑘+1 𝑦 , 𝑠 𝑘+1 𝑧 . En este sentido, 𝑆 𝑜𝑐𝑐𝑢𝑝 representa el conjunto finito de octantes ocupados. Finalmente, 𝑅 𝑚 ,𝑚=1…𝑁 define el conjunto de las 𝑁 funciones parciales que intervienen en las características de navegación 3D del UAV y determinan el progreso factible. En este trabajo, se definen 𝑁=2 parámetros de vuelo, definidos tal que:
donde, 𝑀 𝑑𝑖𝑠𝑡 𝑠 𝑖 → 𝑠 𝑗 es la distancia euclídea entre dos estados cualesquiera y 𝑀 𝑡𝑟𝐷 es la distancia en línea recta entre 𝑞 𝑖 y 𝑞 𝑔 , lo cual busca alcanzar una minimización de distancia en trayectoria de vuelo directo entra octantes 𝑆 𝑓𝑟𝑒𝑒 .
Por otra parte, es importante destacar que toda batería consume energía, la cual se agota después de un determinado tiempo, entonces, el cálculo de la trayectoria debe considerar este consumo. Por una parte, para aeronaves comerciales, el cálculo del consumo se define por medio de la relación:
donde 𝑚 representa la masa del vehículo y 𝑐 el gasto másico de combustible. La consecuencia del consumo de combustible significa la masa es una función del tiempo. Por lo tanto, cuanto menor sea la variación de la masa, menor será el consumo de combustible.
No obstante, debido a las características del UAV tomado para este trabajo (se considera una masa constante puesto que se requiere de una alimentación de energía exclusiva de baterías eléctricas), se buscar realizar una estimación de energía consumida durante la trayectoria de vuelo. Entonces, a partir de método de Euler mejorado, se ha realizado una aproximación del cálculo de consumo, lo cual se define como:
donde, 𝑐𝑠𝑚 𝑠 𝑖 → 𝑠 𝑗 representa el consumo de batería para la trayectoria entre los estados vecinos. Trayectoria definida como el área de vuelo 3D, la cual es menor al área total de vuelo desde el punto inicial hasta el punto final de trayectoria en vuelo directo. De esta forma, el área de vuelo se define a partir de los límites definidos por los ejes coordenados 𝑥,𝑦,𝑧 , tal que: 𝑏 1 ≤𝑦≤ 𝑏 2 y 𝑎 1 ≤𝑥≤ 𝑎 2 .
Además, se utiliza una función gaussiana 𝑔 𝑅 𝑚 para determinar la recompensa en la ejecución de una posible acción y se define como:
donde, los valores de coste de transición 𝑠 𝑘 → 𝑆 𝑘+1 , 𝑆 𝑘+1 → 𝑞 𝑔 se han normalizado dentro de los límites 0,1 . Obsérvese cómo cuanto mayor es el esfuerzo 𝑅 𝑚 , menor es la recompensa 𝑔 𝑅 𝑚 y viceversa. Por lo tanto, la ejecución de una acción desde el estado 𝑠 𝑖 a diferentes estados 𝑠 𝑗 produce transiciones de estado a diferentes costes.
Todas estas recompensas pueden expresarse como un vector 𝐺 𝑖, 𝑗 de parámetros de vuelo como:
donde 𝜉 es un valor de recompensa negativo predefinido en cada estado perteneciente a 𝑆 𝑘+1 . Se debe notar que los valores de la distribución de probabilidad de las funciones 𝑔 𝑅 1 ,𝑔 𝑅 2 ,…,𝑔 𝑅 𝑁 son independientes y el conjunto de vectores de respuesta 𝐷 son mapeos de 𝑆× 𝑆 𝑓𝑟𝑒𝑒 . En consecuencia, este mapa se genera con una distribución de probabilidad independiente del tiempo. Esto significa que la probabilidad de pasar de un instante al siguiente no cambia.
Por lo tanto, el mejor valor de recompensa del vector 𝐷 genera la mejor trayectoria final 𝑥 , denotada por 𝜌 𝑥 𝐹 , definida por un grafo finito etiquetado con vértices 𝑆 𝑥 ∈ 𝑆 𝑓𝑟𝑒𝑒 .
2.1 Ejemplo de aplicación
Para explicar la metodología, a continuación, se plantea un problema de planificación de trayectoria, donde el punto inicial se define como 𝑞 𝑖 ∈ 𝑠 𝑘 (definido como estado actual), mientras que el punto meta se define como 𝑞 𝑔 . En este sentido, se considera un octante maestro que contiene un obstáculo en su interior. La Figura 2 muestra el escenario inicial, así como los diferentes estados 𝑆 𝑘+1 (observables y vecinos) que pueden convertirse en un nuevo 𝑆 𝑘 . En este caso, en 𝑡=0 , el costo de moverse a la derecha, al frente o hacia abajo, implica el mismo costo. Esta situación aparece debido a la simetría inherente a la metodología de descomposición, en frente a tal situación, el azar decide el siguiente estado.
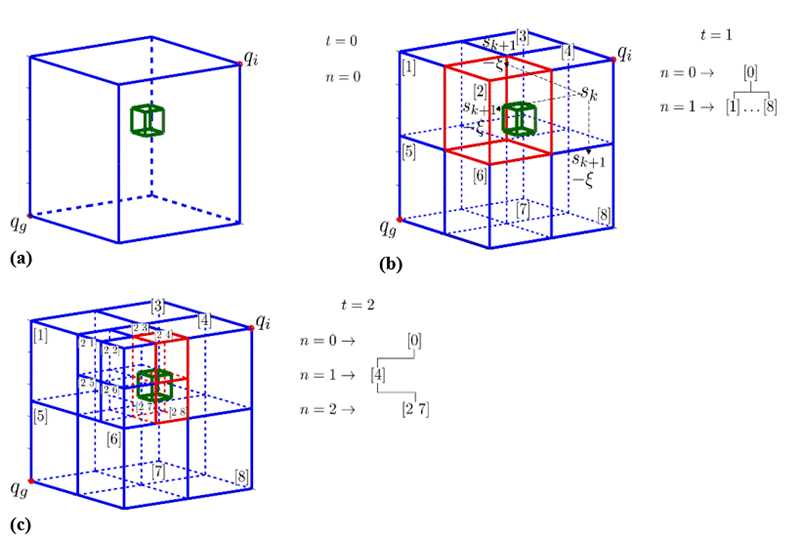
Figura 2: Ejemplo de proceso de inicio MACD de recompensa recursiva (3D-PTDR). (a) Entorno completo. (b) Primer nivel MACD 𝑛 = 1. (c) Segundo nivel MACD 𝑛 = 2.
Como puede verse, el árbol octante se divide en diferentes niveles de octantes con diferentes características dimensionales en diferentes ubicaciones espaciales. Con el objetivo de obtener el conjunto finito de espacios libres de colisiones 𝑆 𝑓𝑟𝑒𝑒 , MACD se realiza recursivamente. Por otra parte, dado que un estado no puede apuntar a sí mismo y sólo puede visitarse una vez, cuando se visitan y evalúan los 𝑆 𝑘+1 estados, se selecciona uno de ellos produciendo un movimiento de reenvío (véase la Figura 2b). Por tanto, el estado seleccionado es el nuevo punto inicial 𝑠 𝑘 , y el proceso se repite de nuevo (véase la Figura 2c). La estructura de red mostrada indica un movimiento de avance 𝑠 𝑘 hacia el estado inmediatamente siguiente 𝑠 𝑘+1 . Este movimiento es independiente de cualquier estado anterior 𝑠 𝑘 .
Los principales límites del entorno han sido definidos desde las coordenadas iniciales 𝑞 𝑖 = 𝑥 𝑖 , 𝑦 𝑖 , 𝑧 𝑖 hasta la meta 𝑞 𝑔 ≡ 𝑥 𝑓 , 𝑦 𝑓 , 𝑧 𝑓 , resultando una forma rectangular, siendo 𝑒𝑛𝑣 = ( ( 𝑥 𝑖 , 𝑥 𝑓 ), ( 𝑦 𝑖 , 𝑦 𝑓 ), ( 𝑧 𝑖 , 𝑧 𝑓 )). Cada obstáculo se define como ℎ 𝑖 𝑥, 𝑦, 𝑧 ∈ ℝ 3 → 𝑥, 𝑦, 𝑧 =λ, y este es definido como:
donde ℎ 𝑖 (𝜆) → 𝑖 > 0 representa un conjunto de obstáculos estáticos.
La Figura 2a muestra la definición del entorno (líneas azules) como nodo principal 𝑛 = 0 con un obstáculo ℎ 1 (λ) situado en su interior (recuadro líneas verdes). Una vez realizada la primera descomposición (ver Figura 2b), un primer nivel octeto 𝑛 = 1 → { (1) . . . (8)} se genera con nodos que tienen diferentes propiedades de ocupaciones. Cada uno pertenece a 𝑆 𝑓𝑟𝑒𝑒 si no hay ℎ 𝑖 (λ) dentro de los límites de su octante ( 𝑠 𝑘 ∩ ℎ 𝑖 (λ)=0) (líneas azules), o a 𝑆 𝑜𝑐𝑐𝑢𝑝 si el octante está parcial o totalmente ocupado por el obstáculo 𝑠 𝑘 ∩ ℎ 𝑖 (λ)=1 ∨ 𝑠 𝑘 ∈ ℎ 𝑖 (λ) (líneas rojas).
El primer paso consiste en determinar el octante contenedor 𝑞 𝑖 (para este ejemplo, es 𝑛 = 1 → {(4)}). En caso de detección de obstáculos en {(4)}, se realizaría una descomposición recursiva en la ubicación. En este nivel, el nodo {(4)} es el nuevo estado inicial 𝑠 𝑘 y los vecinos observables 𝑆 𝑘+1 son los nodos {(2) (3)} y {(8)}. En esta fase, el modelo de estado se representa en la Figura 3.
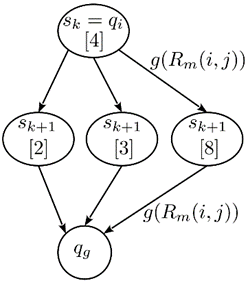
Figura 3: Distribución de probabilidad para los estados discretos, los cuales se derivan de la matriz multidimensional de dimensiones 𝑀 × 𝑀 × 𝑁, donde 𝑀 es el número de estados y 𝑁 es el número de funciones parciales 𝑅( 𝑚 ) con 𝑚 = 1 . . . 𝑁, que intervienen en la navegación 3D del UAV.
De esta forma, se construye una matriz multidimensional con la información del modelo de estado y los valores de recompensa. El objetivo es encontrar las respuestas parciales procedentes de la primera fila y la última columna, y dividirlas en dos vectores de prioridad de transición ( 𝐷 1 , 𝐷 2 )∈ ℝ 𝑀−2 . Utilizando el vector de prioridad 𝔭 y el desplazamiento 𝜉, los vectores 𝐷 1 y 𝐷 2 entregan distribuciones parciales de recompensa a un posible siguiente estado.
Entonces, el vector de prioridad de transición 𝐷 1 se construye con el conjunto de columnas 𝑗 = 2 . . . (𝑀 − 1) y la fila 𝑖 = 1 tal que:
El segundo vector de prioridad de transición, 𝐷 2 , se construye con el conjunto de filas 𝑖=2. . . (𝑀−1) y la columna 𝑗 = 𝑀.
Finalmente, el vector de recompensa final 𝐷 expresado como la suma de 𝐷 1 y 𝐷 2 contiene el valor óptimo que señala el mejor estado para continuar la búsqueda del camino ρ 𝑥 .
Para continuar con el ejemplo de la Figura 2, se asume que 𝑥 = 𝑏𝑒𝑠𝑡(𝐷) apunta hacia el estado {(6)}. Sin embargo, el estado {(2)} está ocupado (pertenece a 𝑆 𝑜𝑐𝑢𝑝 ), por lo que se invoca a MACD, creando un nuevo nivel en la estructura de datos, compuesto por {(2 1) (2 2) (2 3) (2 4) (2 5) (2 6) (2 7) (2 8)} (véase la Figura 2c). Aunque el estado 𝑠 𝑘 permanece en (4), la nueva descomposición en (2) devuelve un nuevo conjunto de vecinos, que se unen a los anteriores y definen el nuevo conjunto 𝑆 𝑘+1 definido por {(3) (2 3) (2 4) ( 2 7) (2 8) (8)}.
Por tanto, es necesario buscar el óptimo dentro de 𝑆 𝑘+1 . Entonces, asumiendo que el mejor nodo desde 𝑠 𝑘+1 es (2 3) (nótese que MACD se invoca una vez hasta ahora) y por tanto el nuevo estado 𝑠 𝑘 se reasigna a (2 3) y en consecuencia, la vecindad del nuevo estado 𝑠 𝑘 , queda conformada por 𝑆 𝑘+1 ={(2 1) (2 4) (2 7) (1) (4)}.
Las acciones anteriores producen el desplazamiento desde un estado 𝑠 𝑘 actual al siguiente mejor estado, y hacia el punto final. Aunque el octante contenedor del mejor estado resultante 𝑥 no contiene el punto de meta, existe la posibilidad de que 𝑥 tenga vecinos en distintos niveles de descomposición. Por lo tanto, el proceso continúa hasta que se alcanza el punto de meta. Una vez completada la fase anterior, el camino óptimo ρ 𝑥 (𝐹) queda totalmente determinado y la búsqueda finaliza.
En realidad, el procedimiento se divide en dos etapas. En primer lugar, se define una ubicación de octante inicial, entonces, si existe un ℎ 𝑖 (𝜆) en el entorno, se realiza una descomposición simple inicial, en consecuencia, se define el octante libre de colisiones que contiene el punto inicial. Una vez asignado el estado inicial 𝑠 𝑘 que también es un ρ 𝑥 inicial, se procede en función de su ocupación. Si 𝑠 𝑘 está libre de colisiones, se asignan los vecinos 𝑆 𝑘+1 , se calculan las recompensas y se localiza el óptimo 𝑥. Por tanto, el mejor estado 𝑥 se convierte en el nuevo 𝑠 𝑘 y se añade a ρ 𝑥 . En el caso que este nuevo 𝑠 𝑘 este ocupado, el proceso requiere otra descomposición en el 𝑠 𝑘 actual, y 𝑠 𝑘 volverá a su estado anterior. El procedimiento finaliza cuando el 𝑠 𝑘 actual contiene el punto objetivo y 𝑠 𝑘 está libre de colisiones.
La metodología descrita presenta varias propiedades, siendo: (a) Define un proceso estocástico en tiempo discreto, entonces, la distribución de probabilidad para un estado futuro depende únicamente de sus valores presentes y es independiente del pasado del estado actual. (b) La suma de las prioridades definidas en el vector 𝔭 no es igual a 1. 𝑖=1 𝑁 𝔭 𝑖 𝑖≠1. (c) La suma de los valores de cada vector de prioridades, no es igual a 1. 𝐷 1 ≠1 y 𝐷 2 ≠1.
Finalmente, es importante destacar que la descomposición discreta del entorno da lugar a octantes cada vez más pequeños y de distintos tamaños. El nivel de descomposición de los octantes es variable en función de dos objetivos que deben cumplirse, siendo: (1) El diseñador define el nivel máximo de descomposición (tamaño mínimo del octante); sin embargo, el algoritmo intenta reducir el coste computacional, en consecuencia, se suele evitar el tamaño mínimo del octante. (2) En cuanto un espacio libre cumple las restricciones definidas, el algoritmo lo selecciona independientemente del tamaño del octante.
Resultados
Con el objetivo de analizar el rendimiento del algoritmo propuesto, se han aprovechado las prestaciones del sistema de cálculo numérico “MATLAB versión 9.9.0.1467703 (R2020b)”. El algoritmo se ha ejecutado en “Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 GHz, 1 procesador físico; 4 núcleos; 8 hilos” con 8Gb RAM y S.O. Ubuntu Linux 20.04.2 LTS.
Para evaluar el algoritmo 3D-PTDR propuesto, se han diseñado 10 escenarios de simulación (𝕎 que incluyen uno o más obstáculos estáticos en su interior), no obstante, para efectos de simplificación en la Tabla 2 se detallan 2 escenarios. En concreto, cada escenario tiene dimensiones espaciales de 𝑋= 100𝑚), 𝑌=100𝑚), 𝑍=100 (𝑚 . De esta forma, cada escenario ha sido sometido a 10 ejecuciones, resultados que han sido comparados con los resultados generados por MACD.
Tabla 2: Definición de los distintos 𝕎 3D para los ejemplos de simulación. Tanto las ubicaciones de los objetivos como las de los obstáculos y sus dimensiones se han definido en metros (m).
| Ubicaciones de la trayectoria objetivo (m) | Obstáculos (m) | |||||||||||||
| # | Inicio | Meta | Dimensiones | Ubicación | ||||||||||
| # | x | y | z | x | y | z | ||||||||
| 1 | 100 | 100 | 42 | 0 | 0 | 24 | 1 | 12 | 12 | 50 | 40 | 30 | 25 | |
| 2 | 96 | 60 | 30 | 12 | 15 | 45 | 1 | 10 | 10 | 10 | 40 | 40 | 50 | |
| 2 | 5 | 5 | 5 | 60 | 60 | 80 | ||||||||
| 3 | 6 | 6 | 6 | 70 | 80 | 50 | ||||||||
| 4 | 15 | 15 | 15 | 70 | 70 | 70 | ||||||||
En específico, la Tabla 2 se divide en 2 columnas principales que son: “Ubicaciones de la trayectoria objetivo” y “Obstáculos”. En la primera columna se detallan las ubicaciones específicas de los objetivos inicio y meta (se han definido diferentes objetivos 3D para cada escenario), mientras que en la segunda columna se muestran las dimensiones, ubicaciones y número de obstáculos para cada escenario. Es importante resaltar que, en el primer escenario, se ha localizado un obstáculo, mientras que, en el segundo escenario se han definido cuatro obstáculos.
La Figura 4 muestra el ejemplo de trayectoria construida por 3D-PTDR para el primer escenario, donde las cajas negras son los obstáculos ℎ𝑖(𝜆), las estrellas verdes muestran el conjunto de vértice en el estado 𝑠 𝑘 y la línea naranja muestra la trayectoria final ρ 𝑥 (𝐹). De esta forma, la Figura 4(a) muestra una vista 3D de la trayectoria construida mediante 3D-PTDR en el primer escenario, mientras que la Figura 4(b) muestra una vista perpendicular (desde el plano ortogonal al eje-z) del mismo escenario #1. Finalmente, la Figura 5 representa los resultados 3D-PTDR y MACD para el escenario #2, donde las Figuras 5(a) y 5(c) muestran una vista 3D, finalmente, las Figuras 5(b) y 5(d) muestran los resultados de ρ 𝑥 con vista perpendicular al eje-z.
Discusión
Con el fin de proporcionar una comparación de rendimiento entre los algoritmos descritos, la Tabla 3 detalla los resultados en tiempo de descomposición discreta a lo largo de cada escenario, el número de octantes libres de colisión 𝑆 𝑓𝑟𝑒𝑒 , el número de nodos generados en la trayectoria final ρ y la longitud de la trayectoria. Es importante destacar que cuando un obstáculo ℎ 𝑖 (𝜆) se cruza con una descomposición de octantes, MACD continúa recursivamente hasta el nivel 𝑛 predefinido (por esta razón el tiempo de búsqueda de MACD es considerablemente mayor que 3D-PTDR), además, MACD requiere cálculos adicionales definidos por el planificador de Dijkstra’s para obtener el camino óptimo final ρ.
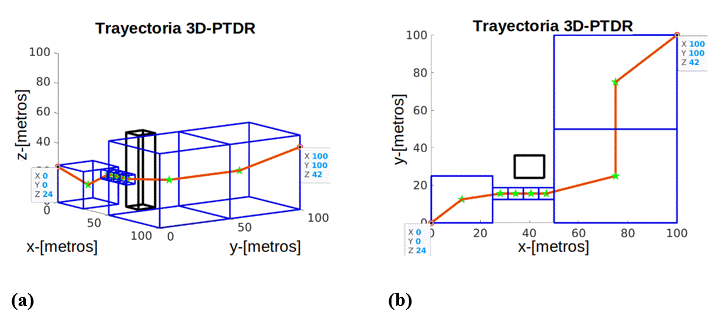
Figura 4: Resultados de trayectoria del escenario #1 visto desde diferentes perspectivas. (a) Trayectoria generada por 3D-PTDR con perspectiva de vista 3D (54, 12). (b) Resultados del escenario #1 con la vista desde el 𝑝𝑙𝑎𝑛𝑜 (𝑥, 𝑦).
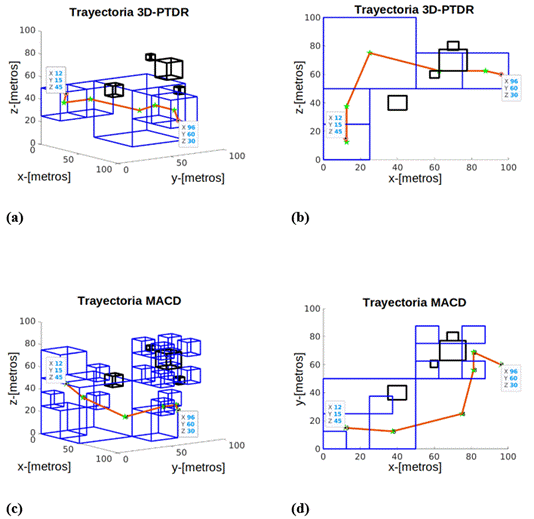
Figura 5: Escenario #2, visto desde diferentes perspectivas. (a) Trayectoria generada por 3D-PTDR con perspectiva de vista 54°, 12° . (b) Trayectoria generada por 3D-PTDR con perspectiva de vista del plano 𝑥, 𝑦 . (c) Trayectoria generada por MACD con perspectiva de vista (54,12). (d) Trayectoria generada por MACD con perspectiva del plano (𝑥, 𝑦).
Tabla 3: Resultados de las diversas ejecuciones sobre los escenarios descritos.
| - | MACD | 3D-PTDR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| # | Tiempo de descomp. (s) | Tiempo Dijkstra (s) | #S free | # 𝛒 | Longitud (m) | Tiempo de descomp. (s) | #S free | # 𝛒 | Longitud (m) |
| 1 | 0.14265 | 0.00189 | 65 | 7 | 173.43682 | 0.00166 | 43 | 9 | 177.36750 |
| 2 | 0.15187 | 0.00119 | 55 | 5 | 132.73110 | 0.00016 | 19 | 6 | 146.76870 |
| 3 | 0.17352 | 0.01513 | 107 | 6 | 130.32670 | 0.00514 | 27 | 7 | 152.44530 |
| 4 | 0.12765 | 0.00130 | 44 | 7 | 175.81597 | 0.00017 | 19 | 6 | 171.25050 |
| 5 | 0.18137 | 0.00314 | 77 | 7 | 147.79795 | 0.00022 | 27 | 5 | 121.72630 |
| 6 | 0.41876 | 0.00158 | 49 | 5 | 152.67823 | 0.00476 | 11 | 6 | 199.9279 |
| 7 | 0.29923 | 0.00147 | 61 | 5 | 152.67823 | 0.00018 | 11 | 6 | 169.2270 |
| 8 | 0.26390 | 0.00118 | 55 | 9 | 184.97604 | 0.00023 | 19 | 5 | 139.02570 |
| 9 | 0.23216 | 0.00118 | 66 | 7 | 158.83471 | 0.00339 | 67 | 13 | 127.6446 |
| 10 | 0.15697 | 0.00088 | 42 | 6 | 173.12528 | 0.01133 | 27 | 7 | 208.0392 |
De esta forma, la Tabla 4 muestra las diferencias en términos porcentuales entre los algoritmos. Se distingue una diferencia sustancial en los distintos parámetros. Por lo tanto, la diferencia en el tiempo de cálculo es evidente debido al tiempo adicional de Dijsktra en MACD. Por ejemplo, en el primer escenario, el algoritmo 3D-PTDR sólo necesita el 1,15248% del tiempo computacional que MACD necesita para la descomposición discreta, el 66,15385% del total de número de 𝑆 𝑟𝑓𝑒𝑒 que MACD, +28,57143% más nodos que MACD necesita para construir ρ, por último, la trayectoria 3D-PTDR es +2,26635% más largo que MACD.
Tabla 4: 3D-PTDR vs. MACD (%) muestra los recursos medios (tiempo de descomposición (s), número de 𝑆 𝑓𝑟𝑒𝑒 y número de nodos en la ruta final “ρ”) utilizados para 3D-PTDR en comparación con MACD.
| - | 3D-PTDR vs MACD | |||
| # | Tiempo de descomp. (s) | #S free | # 𝛒 | Longitud (m) |
| 1 | 1.15248 | 66.15385 | +28.57143 | +2.26635 |
| 2 | 0.11041 | 34.54545 | +20.00000 | +10.57597 |
| 3 | 0.02966 | 0.25233 | +16.66667 | +16.97165 |
| 4 | 0.13725 | 43.18182 | 85.71429 | 97.40327 |
| 5 | 0.12302 | 35.06494 | 71.42857 | 82.35993 |
| 6 | 1.13405 | 22.44898 | +20.00000 | +30.94722 |
| 7 | 0.06218 | 31.14754 | +40.00000 | +10.83898 |
| 8 | 0.08714 | 34.54545 | 55.55556 | 75.15876 |
| 9 | 1.45357 | +1.51515 | +85.71429 | 80.36316 |
| 10 | 7.18182 | 64.28571 | +16.66667 | +20.16685 |
En términos generales, el tiempo computacional conseguido en 3D-PTDR mejora significativamente, debido a la forma en la que se divide 𝕎, por lo que el número de 𝑆 𝑓𝑟𝑒𝑒 también es menor.
Conclusiones
El primer paso relevante para completar la tarea de planificación de trayectoria 3D, ha estado enfocado en el trabajo sobre un entorno en forma de malla adaptativa, lo cual ha dado lugar a la metodología para la descomposición discreta del entorno 3D. De esta forma, los resultados de la descomposición del entorno han sido utilizados para alcanzar las trayectorias 3D deterministas. No obstante, es importante destacar que el refinamiento 3D en los diversos experimentos ha sido mínimo (teniendo en cuenta diversas restricciones de vuelo, además de las características geométricas de la 𝕎), lo cual provocado un tiempo computacional de cálculo aceptable.
Luego de revisada la bibliografía referente a la planificación de trayectoria 3D en entonos discretos, se ha llegado a un punto relevante en que se menciona de forma reiterada que diversas metodologías requieren de planificadores adicionales como los de Dijkstra, A*, D*, entre otros, mientras que 3D-PTDR evita la necesidad de utilizar planificadores adicionales. Por otra parte, es importante resaltar que, al proponer una metodología que considera un conjunto de condiciones para la determinación de trayectorias (restricciones de vuelo, que además puede ser ampliada por el lector), las cuales son sometidas a evaluación simultánea. Dando como resultado un conjunto de recompensas, a partir de las cuales se determina la trayectoria final óptima, con un tiempo computacional reducido y menor complejidad de cálculo, en comparación con técnicas similares aplicadas a la tarea de planificación de trayectorias 2D y 3D.
Finalmente, se puede destacar que los experimentos y resultados han demostrado que la metodología propuesta alcanza su objetivo final de generación de trayectoria 3D, no obstante, queda abierta la posibilidad de incrementar las funciones de optimización de trayectoria, tanto en geometría como en restricciones de vuelo.
Conflicto de interés
Los autores declaran que no existen conflictos de interés de naturaleza alguna con la presente investigación.
Contribución de los autores
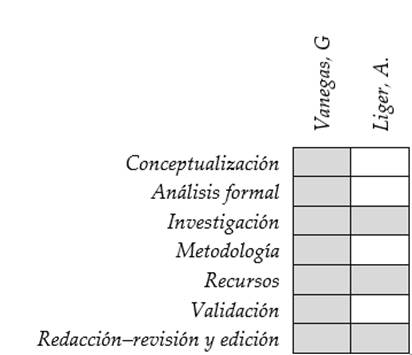
En concordancia con la taxonomía establecida internacionalmente para la asignación de créditos a autores de artículos científicos (https://casrai.org/credit/ ). Los autores declaran sus contribuciones en la siguiente matriz: