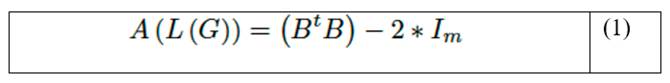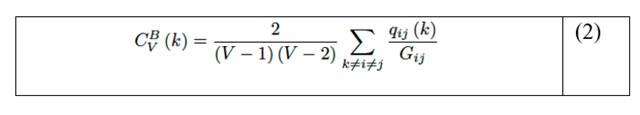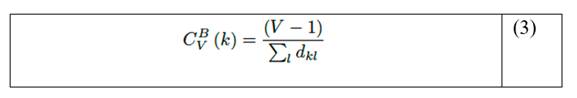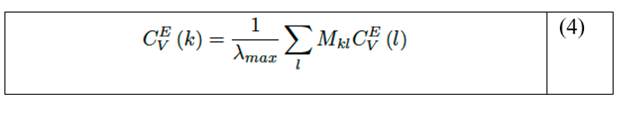Introducción
La identificación de elementos importantes en sistemas eléctricos de potencia (SEP), consiste en determinar cuáles de estos elementos tienen mayor relevancia frente a una, o varias condiciones de operación particulares. Por ejemplo, pueden mencionarse los trabajos de diversos autores [1-3], donde a partir de evaluación de flujos de potencia en el SEP, seleccionan los elementos que, puestos fuera de servicio, producen el mayor racionamiento a la carga.
Otros investigadores se han centrado en encontrar los elementos que afectan en mayor medida la vulnerabilidad del SEP [4, 5], elementos con mayor potencial para desencadenar fallas en cascada en el SEP [6], o identificar los elementos que afectan la confiabilidad del SEP [7].
Recientemente, una línea de investigación en el análisis de sistemas de potencia se basa en la teoría de redes para obtener soluciones computacionalmente más rápidas, pues no contemplan la evaluación de las ecuaciones físicas que rigen el comportamiento del sistema, sino que, se basan únicamente en las características topológicas de la red [8].
Un enfoque ampliamente utilizado para la evaluación de importancia de elementos en una red, considerando exclusivamente la topología, tiene como referencia las medidas de centralidad. De acuerdo con Newman [9], los investigadores tratan de responder la siguiente pregunta: ¿Cuáles son los nodos más importantes o centrales en una red? Pero la mayoría de las medidas de centralidad están definidas para los nodos del sistema, algunos científicos han hecho extensiones de la centralidad para nodos [10] a los enlaces; a partir de ello puede entonces responderse la interrogante anterior, pero desde la perspectiva de los enlaces de la red.
En el caso de los SEP, los enlaces (que pueden representar líneas de transmisión de energía o transformadores eléctricos) revisten más importancia que en otro tipo de sistemas. Como indican Ortiz et al. [11] las medidas de centralidad (consideradas sobre los enlaces) son de utilidad, pues, permiten conocer la importancia que tiene un enlace, que se interconecta con otros enlaces para permitir el flujo de energía eléctrica entre fuentes y cargas. Algunos autores [11, 12] se basan en una transformación de la red original a una equivalente, donde los enlaces de la original se cambian a nodos en la red equivalente, y en esta, pueden evaluarse métricas de centralidad de nodos, logrando de forma indirecta determinar la importancia de los enlaces de la red original. Esta transformación tiene su sustento en el concepto matemático denominado linegraph [13], donde a partir de un grafo G se crea un nuevo grafo equivalente L(G) cuyos nodos representan los enlaces de G.
En este trabajo, a partir de la transformación de una red G, que representa la topología de un SEP, a una nueva red L(G) mediante linegraph [13] y la evaluación de medidas de centralidad en redes, se plantea cómo clasificar los enlaces (líneas de transmisión y/o los transformadores) de la red G de acuerdo con su nivel de importancia. Para ello se emplea la agregación de listas ordenadas, lo que permite combinar varias en una sola. La agregación es un problema común en ciencias sociales, estadísticas y otros campos, en los que se deben combinar diferentes listas ordenadas de acuerdo con algún criterio [14].
Trabajos previos
Autores como los citados en [15] y [8] analizan el sistema eléctrico italiano (HVIET) y el sistema eléctrico venezolano (SENTRONCAL), respectivamente, desde la perspectiva de las redes complejas. Se determina la importancia de la topología en la caracterización de la red, pero las evaluaciones y clasificaciones de los elementos se centran en los nodos del sistema eléctrico.
Por otra parte, Hines y Blumsack [16] indican que existe una clara vinculación entre la topología de la red y la vulnerabilidad de la misma. En este trabajo [16] se define una medida denominada “distancia eléctrica equivalente entre pares de nodos”, basada en medidas de centralidad de información [17, 18].
Ciertos investigadores [19] evalúan diversos sistemas eléctricos de la literatura (IEEE30, IEEE57 y IEEE 118) a partir de medidas de centralidad modificadas para incorporar parámetros eléctricos, las medidas consideradas son: Degree centrality, Closeness centrality y Betweenness centrality, todas son evaluadas en los nodos de la red. Posteriormente, Nasiruzzaman y Pota [6] plantean un método para la evaluación de la estabilidad de sistemas de potencia a partir de la teoría de redes, utilizan como medida de centralidad una extensión del concepto de Betweenness centrality a Edgebetweenness centrality; es decir, una medida de centralidad para enlaces de red.
En el artículo [19] se propone un modelo mejorado del índice closeness centrality, para determinar nodos críticos en procesos de fallas en cascadas en redes. Chen et al. [5] proponen un índice denominado “weighted line betweenness” con el cual identifican líneas de transmisión críticas (enlaces de la red), no solo por su capacidad de potencia eléctrica, sino por su disposición topológica en la red. Amani y Jalili [4] presentan una revisión relacionada con el análisis de vulnerabilidad y resiliencia en sistemas de potencia a partir de la teoría de redes complejas. Identifican un conjunto de medidas e índices, específicamente cabe destacar un resumen donde mencionan medidas específicas para nodos y enlaces, algunas son medidas de centralidad o medidas de centralidad adaptadas a redes eléctricas.
En el trabajo de Nakarmi et al. [7] realizan una clasificación de análisis de confiabilidad en sistemas de potencia a partir de grafos y la interacción de sus elementos. Una subclasificación importante que realizan es la “identificación de componentes críticos”, es un tipo de análisis de confiabilidad donde se enfocan en encontrar nodos/líneas de transmisión (enlaces) críticos, mediante el análisis de las propiedades estructurales de los grafos, utilizando medidas de centralidad estándar o mediante la definición de nuevas métricas basadas en grafos (por lo general incorporan características eléctricas a la medida estándar) [20-22].
En el trabajo de Bröhl y Klaus [10] indican que existe abundancia de métodos para medir la centralidad de los nodos individuales, pero hay pocas métricas para medir la centralidad de los enlaces individuales. Por ello, proponen modificaciones a los conceptos de centralidad ampliamente utilizados para los nodos, para poder aplicarlos a enlaces en las redes y así identificar enlaces, o conjuntos de enlaces, importantes. Se enfocan en tres índices:
El trabajo de Ortiz et al. [11] utilizan el concepto matemático denominado linegraph [13], donde a partir de un grafo original G, se puede crear un nuevo grafo L(G) cuyos nodos representan los enlaces de G. Esto supone poder aplicar las medidas tradicionales de centralidad de nodos a los enlaces de la red, a partir de esa red nueva L(G). Su propuesta permite identificar enlaces de importancia en la red, se aplican los índices de centralidad a enlaces en redes sociales (Facebook), pero indican, que esto pudiera permitir conocer la importancia que tiene un enlace interconectado con otros para permitir el flujo de información entre orígenes y destinos.
Este trabajo propone, a partir del concepto de linegraph L(G), [13] clasificar los enlaces importantes en redes eléctricas, cuantificando valores de centralidad de los mismos. Posteriormente, se realiza una agregación de las listas ordenadas anteriores, para generar una única clasificación de importancia de los elementos, que considere e integre las diversas medidas de centralidad empleadas. Adicionalmente, se compara la distribución de los valores de centralidad de diferentes redes eléctricas analizadas en la literatura.
Materiales y métodos
Definiciones preliminares
Grafo
Una red, incluidos los sistemas eléctricos de potencia, puede ser modelada como un grafo G = (V,E), donde V = {v1, ..., vn} representa el conjunto de nodos (buses de conexión del sistema); y E = {e1, ..., em} el conjunto de enlaces que conecta los nodos del grafo (líneas de transmisión y transformadores). El número de nodos se define como n = |V |; y el número de enlaces como m = |E|.
Entonces, A(G) = (aij) es la matriz de adyacencia del grafo G de orden n x n, donde aij indica si hay conexión entre los nodos vi y vj , aij = 1 si vi y vj están conectados, y aij = 0 cuando no.
Por otra parte, B(G) = (bij) representa la matriz de incidencia de G con un orden n x m, donde bij = 1 si vi y vj son incidentes, y bij = 0 cuando no.
Linegraph
El Line Graph L(G) es un grafo cuyos nodos representan los enlaces del grafo original G y la matriz A(L(G)). La ecuación (1) representa la matriz de adyacencia de L(G) de orden m x m.
Entonces:
Donde Im es la matriz identidad de dimensión m x m.
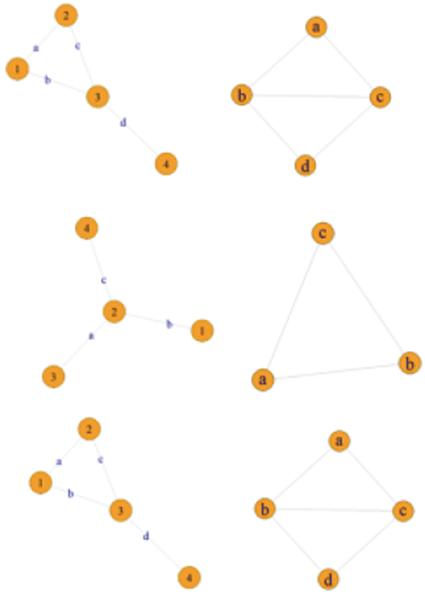
En la Figura 1 se muestran ejemplos para grafos simples (izquierda) con sus correspondientes L(G) (derecha). Note que en los grafos L(G), no se consideran los nodos originales y se obtiene un grafo en los que los nodos corresponden a los enlaces. Por ejemplo, en el grafo mostrado en la parte superior izquierda de la Figura 1, con los nodos {1, 2, 3} y enlaces a = (1, 2) y b = (2, 3) se transforma a otro grafo con solo dos nodos {a, b} y un único enlace {2}.
Medidas o índices de centralidad Betweenness centrality (centralidad de intermediación [23]).
De acuerdo con [24], la betweenness centralit de un nodo k puede definirse según la ecuación (2):
Donde {k, i, j} εV y qij es el número de caminos más cortos entre los nodos i y j pasando por el nodo k. Gij es el número total de caminos más cortos entre los vértices i y j.
Closeness centrality (centralidad de cercanía [23]). La centralidad de la cercanía del nodo (para un nodo k) se define de acuerdo con la ecuación (3):
Con {k, l} εV y donde dkl denota la longitud del camino más corto desde el nodo k al nodo l.
Eigenvector centrality (centralidad de vector propio [23]). La centralidad del vector propio del nodo (del nodo k) se define como, ecuación (4), la k-ésima entrada del vector propio v correspondiente al valor propio dominante λmax de la matriz M, que derivamos de la ecuación del vector propio M 𝑣 = λ 𝑣 {k, l} εV . Donde, M denota la matriz de adyacencia A(v)ε{0, 1}V xV de una red, con 𝐴 𝑖𝑗 (𝑣) = 1 si hay un enlace entre los nodos i y j, y 0 en caso contrario.
Procedimiento para la clasificación de los enlaces de acuerdo con su importancia
Sea un SEP, considerando exclusivamente su topología, se define el grafo G = (V,E), entonces se puede determinar L(G) cuyos nodos representan los enlaces del grafo original G. Luego, a partir de este grafo equivalente L(G) se determinan:
Para cada uno de los enlaces del sistema eléctrico de potencia, pero representados como nodos en el grafo equivalente L(G), se obtienen las tres medidas de centralidad mencionadas, se normalizan y se ordenan de mayor a menor, lo cual permite clasificar la importancia del enlace de acuerdo con el índice dado.
Entonces, pueden clasificarse como importantes enlaces de acuerdo con un valor preestablecido del índice, por ejemplo, puede establecerse que los enlaces con valores mayores a 0.9 son los más importantes de la red, o algún otro criterio preestablecido por el decisor.
Luego de tener cada una de las listas o rankings, por cada índice de centralidad considerado, es posible generar una clasificación general de los elementos que combine las características que mide cada índice por separado, y, de aquí, determinar un único orden de importancia para cada uno de los elementos.
En este trabajo se utiliza un método para la combinación de listas ordenadas de acuerdo con su importancia, basado en determinar un orden compromiso, en el que, las diferencias o distancias con las listas ordenadas sean mínimas. Naturalmente, para la determinación del orden combinado, pueden considerarse cualquier otra técnica (por ejemplo, métodos de decisión multicriterio) [25]. El método de combinación de listas empleado en este trabajo se encuentra en la librería RankAgregg [14] del software R [26]. Las distancias entre el ordenamiento compromiso buscado y cada una de las listas ordenadas se calcula con el índice de similitud de Spearman, mientras que la optimización (minimización de la suma de las distancias) se realiza mediante una heurística basada en el uso del algoritmo Cross-Entropy Monte Carlo [27]. Para problemas grandes, como en toda heurística, no se garantiza una solución óptima.
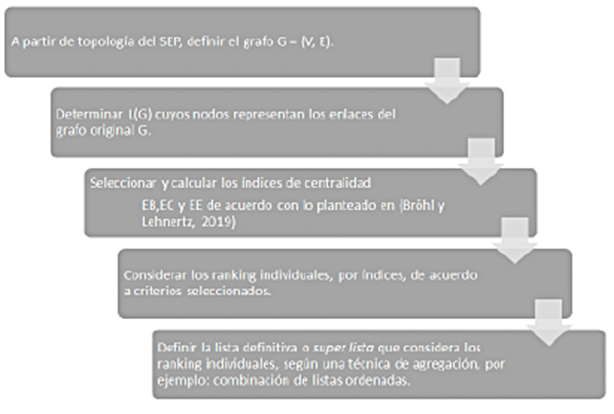
La Figura 2 muestra un gráfico que presenta el proceso completo de agregación para la selección de los grupos de enlaces del SEP considerado.
Ejemplo ilustrativo del procedimiento
Para ilustrar el procedimiento descrito en la Figura 2, consideremos un SEP representado por el grafo de la Figura 3 (izq.). A partir de la técnica linegraph (disponible en la librería igraph [28]) obtenemos el grafo equivalente, ver Figura 3 (der.), donde los enlaces ahora son presentados como nodos. Es decir, por ejemplo, el enlace h que conecta a los nodos 5 y 6 en el grafo de la Figura 3 (izq.), se corresponde con el nodo h del grafo de la Figura 3 (der.).
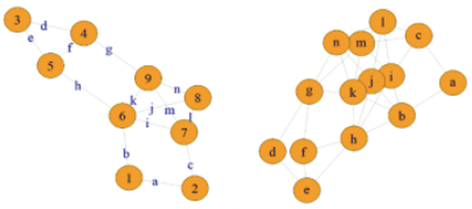
Figura 3 Grafo representativo de un SEP 9 nodos (izq.)-Grafo equivalente (line-graph) de un SEP 9 nodos aplicando linegraph (der.)
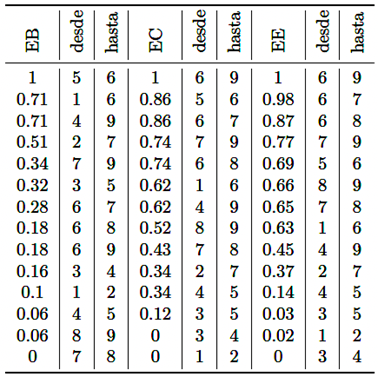
Para el grafo equivalente, Figura 3 (der.), se calculan los índices de centralidad descritos EB, EC, EE. Para ello se emplean las funciones codificadas en la librería igraph [28], del software estadístico R v4.2.2 [26]. La Tabla 1 muestra los valores de los índices de centralidad de los enlaces considerados, ordenados de más importante a menos importante. Note que no existe un enlace que sea el más importante considerando simultáneamente los tres índices de centralidad. De aquí la necesidad de determinar un ranking compromiso. En la Tabla 1 están presentados los elementos (desde-hasta) referidos al grafo Figura 3 (izq.).
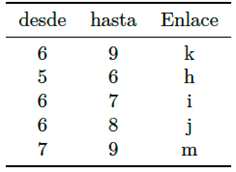
Finalmente, se muestran los cinco elementos más importantes de la lista ordenada combinada o superlista de los enlaces (ver Tabla 2), que considera simultáneamente los tres índices (paquete RankAgregg del software estadístico Rv4.2.2 [26]). Para ello se repite el método, RankAgregg [14], mil veces sobre la red, y las posiciones en la lista, se corresponden con la mayor frecuencia de aparición de los elementos en cada puesto.
Tabla 2 Lista ordenada (5) más importantes, de mayor a menor, de los enlaces del grafo representativo de un SEP 9 nodos
Es importante resaltar que este ordenamiento es robusto, ya que se mantiene aún después de haber ejecutado mil veces el algoritmo de agregación seleccionado (basado en una heurística de optimización).
Resultados y discusión
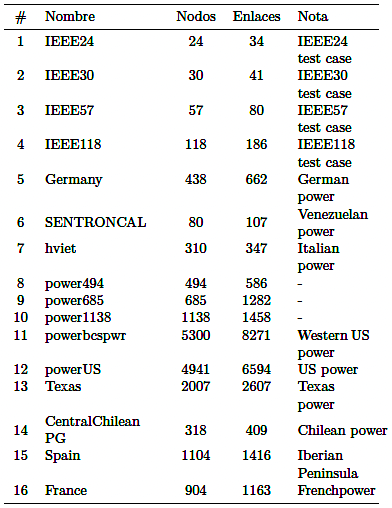
El procedimiento planteado para la identificación de elementos importantes en un sistema eléctrico de potencia, se aplica a un grupo de 16 SEP [29], donde se utiliza exclusivamente la topología asociada a ellos. En la Tabla 3 se muestra el número de nodos y enlaces de cada una de las redes analizadas.
En la Figura 4 se muestra la distribución de las medidas de centralidad para cada una de las redes mostradas en la Tabla 3. Para ello se determina el valor de cada una de las medidas de centralidad consideradas (EB, EC y EE), y se normalizan con la finalidad de comparar las redes de los 16 sistemas eléctricos. Note que para los índices EB y EE, las distribuciones se encuentran casi todas concentradas en valores bajos (a la izquierda) (con la excepción de las redes que poseen pocos nodos (IEEE24 y IEEE30) que presenta una mayor dispersión), mientras el índice EC se encuentra “mejor” distribuido.
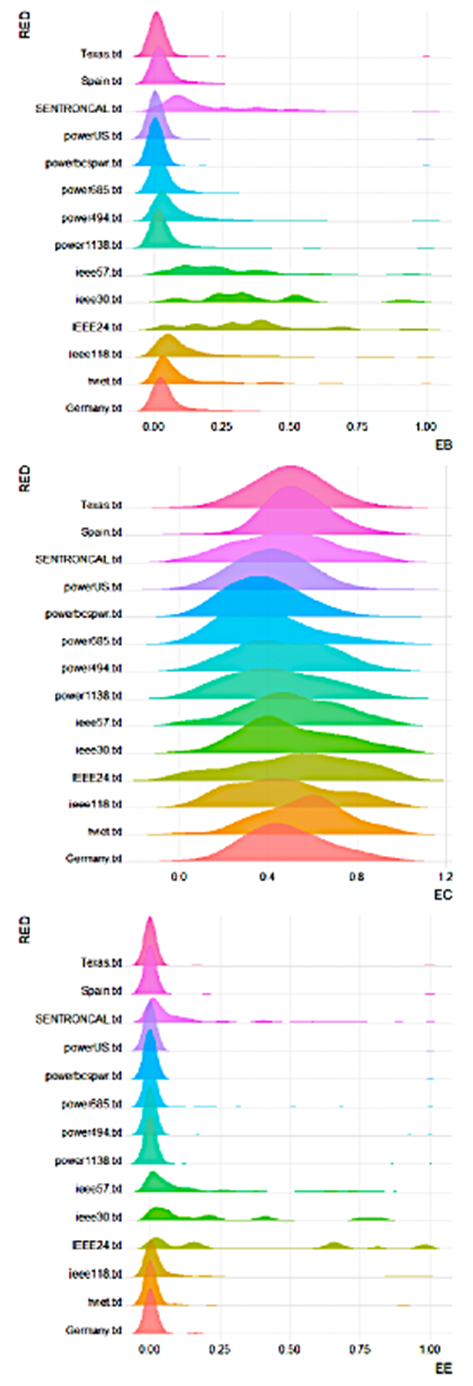
Figura 4 Densidad de probabilidad de los valores de centralidad (EB, EE y EC) en sistemas eléctricos de potencia de la literatura de la Tabla 2
Ahora se considera una red en específico, por ejemplo, la red IEEE57 compuesta por 80 enlaces. En la Figura 5 se muestran los valores de las medidas de centralidad normalizados, para cada uno de los 80 enlaces de la red, donde destacan los enlaces 17, 21 y 33
con los valores más altos en los tres índices evaluados. Es interesante notar que no existe un único enlace más importante (técnicamente un enlace que domine simultáneamente al resto de los enlaces) y que existen índices que evalúan diferentemente la importancia de cada enlace. De aquí, la necesidad de determinar un ranking único que combine las importancias relativas de cada índice.
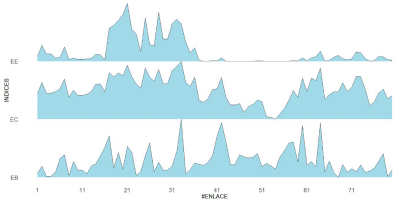
Figura 5 Valores de cada uno de los índices considerados (superior: Betweenness centrality (EB); medio: Closeness centrality (EC); inferior: Eigenvector centrality (EE)) para los enlaces de la red IEEE57.
Para esta misma red, IEEE57, consideremos que el decisor establece un valor mínimo de 0.70 en los índices de centralidad normalizados, para poder considerar el enlace como importante en la red. En la Figura 6 se muestra, a la izquierda, la lista ordenada de enlaces importantes (valores del índice superiores a 0.70), de acuerdo con cada índice en particular; y a la derecha, la topología de la red donde se destacan los enlaces importantes (línea azul), de acuerdo con el criterio mencionado anteriormente.
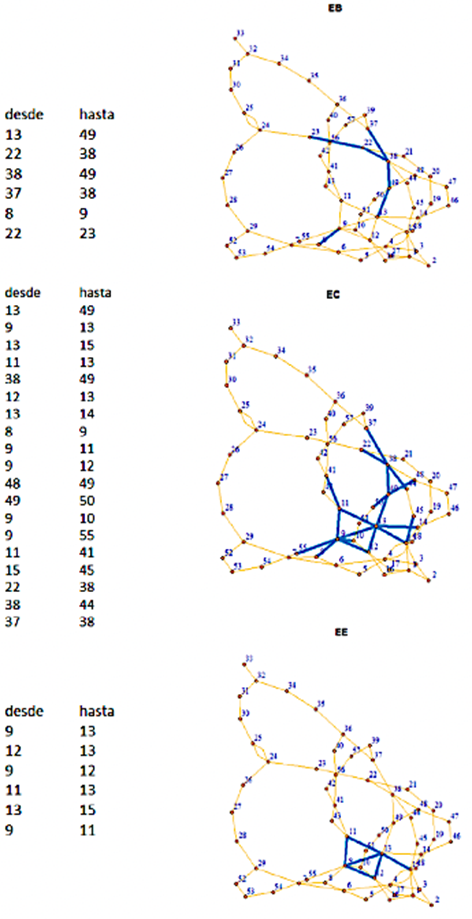
Figura 6 Enlaces importantes de acuerdo con índices de centralidad particulares (superior: Betweenness centrality (EB); medio: Closeness centrality (EC); inferior: Eigenvector centrality (EE)), con sus grafos asociados (los enlaces importantes se destacan en color azul).
Cada índice ordena en forma diferente los enlace. Por ejemplo, el enlace que une los nodos 13-49 (enlace 33) es clasificado como el más importante de acuerdo con los índices de centralidad: Betweenness centrality (EB) y Closeness centrality (EC), pero, en cambio, no aparece en los enlaces importantes de acuerdo con Eigenvector centrality (EE).
Para obtener una clasificación que considere todos los índices de forma simultánea, se aplica el algoritmo de agregación de listas ordenadas, mencionado anteriormente [14]. En la Figura 7 se muestran la red L(G) correspondiente a IEEE57 y los primeros diez elementos de la lista ordenada, que corresponden a los enlaces: 33, 21, 32, 25, 64, 28, 31, 17, 19 y 20 (ordenados de más importante a menos importante).
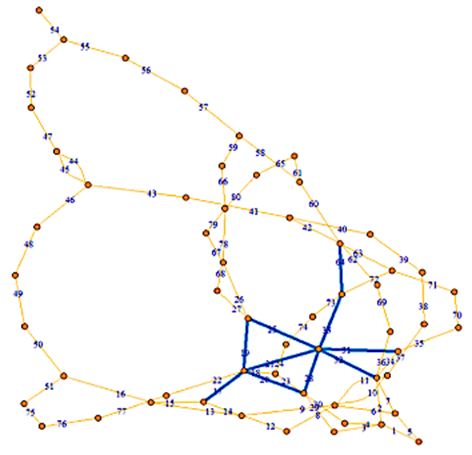
Figura 7 Enlaces importantes de acuerdo con índices de centralidad particulares (superior: Betweenness centrality (EB); medio: Closeness centrality (EC); inferior: Eigenvector centrality (EE)), con sus grafos asociados (los enlaces importantes se destacan en color azul).
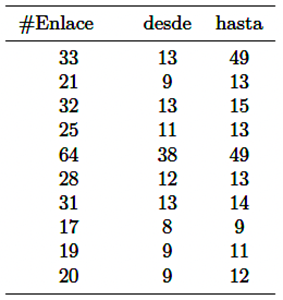
Si se considera el grafo original que representa la red IEEE57, los diez más importantes son los enlaces que se muestran en la Tabla 4.
En la Figura 7 se observa como los elementos más importantes resultan de las listas individuales de los índices de centralidad. Por ejemplo, el elemento que conecta al nodo 13 con el nodo 49 es el más importante en la lista agregada, y, posee los valores más altos en los índices EB y EC, pero está ubicado en la séptima posición para el índice EE (con un valor de 0.65 < 0.7).
El número de enlaces a considerar como importantes puede ser previamente definido por el decisor. Por otra parte, la lista combinada de los enlaces considerados importantes puede ser utilizada como una lista base de entrada en análisis adicionales del sistema eléctrico (por ejemplo, estudios de protección, vulnerabilidad o resiliencia), reduciendo el espacio de análisis al conjunto de elementos importantes. Para el caso particular de la red IEEE57, los primeros diez elementos considerados como importantes, representan menos del 15 % del total de enlaces de la red, lo cual puede reducir el número de posibles evaluaciones que requieran alta exigencia computacional, sobre todo en redes con mayor cantidad de elementos.
Conclusiones
Aquí se propone un esquema de trabajo que permite determinar una lista ordenada, según su importancia, de los enlaces de una red eléctrica, basado en un conjunto de índices de centralidad. Para ello se transforma la red original a una red equivalente que presenta los enlaces como nodos, y, en esta red equivalente se evalúa un conjunto de índices de centralidad (por lo general, los índices de centralidad están desarrollados para nodos y no para enlaces). Utilizamos tres índices de centralidad particulares, pero cualquier conjunto de índices de centralidad pudiera ser empleado.
Posteriormente, desde estas listas se genera una única clasificación, que combina las propiedades consideradas individualmente, con un orden definido de importancia para los elementos de la red.
Este procedimiento fue evaluado en un conjunto de redes que comparten como característica que representan la topología de sistemas eléctricos de potencia, de diversa magnitud, de distintas regiones del mundo y, posiblemente, con criterios de diseño diferentes. Los resultados sugieren que, en general, la distribución estadística estimada de los valores de los índices de centralidad tiene un comportamiento similar.
Los índices evaluados en este trabajo, sugieren, de forma consistente, que los enlaces más importantes están en el “centro” de la red, y que permiten la conexión con enlaces más periféricos. Es importante resaltar que, para la clasificación de los elementos en la red, no se requiere ninguna evaluación de la dinámica específica de la red, incluso, no es necesario ninguna información adicional más allá de la topología de la red (conexiones desde-hasta). Por esto, el procedimiento planteado podría aplicarse para evaluaciones más rápidas que las convencionales, sistemas de potencia con información incompleta, o simplemente como insumo que reduzca las posibles soluciones de una evaluación completa que considere las ecuaciones que modelan el fenómeno eléctrico.
Por otra parte, no considerar el fenómeno eléctrico específico que permite evaluar y clasificar los elementos del sistema de potencia, representa una limitante para este procedimiento, pues, podrían omitirse elementos importantes que solo serían adecuadamente clasificados por la naturaleza en sí del problema.
Se plantea extender en el futuro este procedimiento en dos direcciones. En primer lugar, considerar medidas de centralidad referidas específicamente a sistemas eléctricos, incorporando incluso propiedades de los enlaces (capacidades, impedancias, u otras características). Y, en segundo término, comparar los resultados obtenidos con otros esquemas de evaluación de componentes importantes, basados en análisis funcionales de sistemas eléctricos, por ejemplo: estabilidad, flujos de potencia u otro.