Introducción

Durante los últimos años, el trabajo educativo ha orientado su actuar hacia el desarrollo de habilidades esenciales sustentadas en la capacidad de aprender a aprender más que en la de acumulación del conocimiento (^{Scott, 2015}). Dentro de estas habilidades, se ha fomentado el desarrollo del pensamiento que permite a cada estudiante acercarse al mundo desde diversas perspectivas donde, en particular, la metacognición se sitúa como una de las habilidades que facilitan el proceso de pensar, reflexionar y evaluar el aprendizaje con el fin de comprender cómo se aprende.

Por lo mismo, se ha buscado profundizar respecto a los efectos de la metacognición sobre el desarrollo pedagógico, lo que ha llevado a un significativo incremento de investigaciones que apuntan tanto a niveles educativos primarios como secundarios e incluso universitarios (^{Barrera y Cuevas, 2017}; ^{Mato et al., 2017}; ^{Troncoso, 2013}). Bajo esta lógica, lograr comprender mejor los procesos metacognitivos en el trabajo educativo ha cobrado cada vez mayor relevancia, por cuanto posibilita profundizar respecto a cómo los estudiantes autorregulan sus propios procesos de aprendizaje, sobre todo si pueden elegir qué, cuándo y dónde aprender (^{Steffens y Underwood, 2008}).

Desde el punto de vista del aprendizaje de las matemáticas, uno de los mayores problemas que se ha reconocido en la literatura correspondió a la resolución de ejercicios o problemas, donde se observa una mayor prioridad hacia los resultados, desatendiendo otros procesos mentales vinculados con el “aprender a aprender” y “aprender a pensar”, es decir, hacia los procesos metacognitivos. En otras palabras, se puede decir que el foco de la enseñanza se ha situado preferentemente en los procesos cognitivos por sobre los metacognitivos (^{Mato et al., 2017}), lo que ha generado en los estudiantes aspectos negativos como la carencia de un conocimiento consciente y reflexivo, por ende, no significativo (^{Troncoso, 2013}).

Basados en el contexto de los acelerados cambios sociales, se requiere que los estudiantes desarrollen capacidades para la autonomía en la creación de conocimiento y, al mismo tiempo, que los docentes promuevan situaciones y estrategias de aprendizaje que propicien la enseñanza (^{Rigo et al., 2010}). A pesar del avance con respecto a las estrategias de aprendizaje, aun se observa en la actividad docente estrategias basadas en la transmisión de información que se reducen a mostrar, repetir y copiar el conocimiento transformando esta actividad en una reproducción de saberes y que trae como consecuencia estudiantes pasivos, con dificultades para aprender por sí mismos y regular su aprendizaje. En otras palabras, los estudiantes aprenden sin el desarrollo de la competencia de aprender a aprender, vinculada con el control metacognitivo, que determina al mismo tiempo el desarrollo de habilidades cognitivas y motivacionales (^{Mejía y Haro, 2019}).

En consecuencia, pareciera que la escuela no está cumpliendo a cabalidad con la función de facilitar los procesos de aprendizaje ni con el rol de preparar a los estudiantes para lograr adecuadamente procesos de autoaprendizaje, dado que no se está proporcionado las herramientas necesarias que les permitan ordenar, sistematizar y comprender la información (^{Enríquez et al., 2014}). Con esto, se ha comprendido la urgencia por fomentar habilidades autorreguladoras como la planificación, control, monitoreo y evaluación para una apropiación del conocimiento (Enríquez et al., 2014; ^{Mejía y Haro, 2019}).

En el ámbito del aprendizaje de la matemática, la resolución de problemas ha cumplido un rol fundamental y es uno de sus principales focos de estudio. Sin embargo, tan solo a mediados de la década del setenta la metacognición cobró especial relevancia respecto a su formalización conceptual (^{Valenzuela, 2019}), destacándose la necesidad de modificar los modelos planteados con anterioridad, ya que no suministraban estrategias cognitivas y metacognitivas (^{Flavell, 1976}). En este sentido, las teorías y modelos de resolución de problemas contemporáneos incluyeron elementos de metacognición tales como la planificación, regulación y evaluación del proceso (^{Barrera y Cuevas, 2017}). Pese a estas modificaciones, se ha demostrado empíricamente que los estudiantes “hacen un escaso uso de las estrategias metacognitivas al momento de resolver un problema, además de que se les dificulta tener conciencia sobre los propios procedimientos desarrollados” (Barrera y Cuevas, 2017, p. 8).

También es primordial en matemática el desarrollo del pensamiento lógico, definido como el proceso cognitivo y metacognitivo que se genera a partir de las interacciones de las experiencias y acciones durante la solución de un problema. Dentro de este, el razonamiento hipotético surge como producto de procesos metacognitivos que incluyen la formulación de estrategias, organización de la información, ubicación de los recursos, monitorización y evaluación del proceso, ligados a destrezas cognitivas básicas como la percepción, atención, memoria, pensamiento, razonamiento y lenguaje. La evidencia empírica ha mostrado que, si el problema no se desarrolla en base a procesos cognitivos y metacognitivos en conjunto, no es posible elaborar y/o configurar un plan fundamentado en estrategias que, en gran parte de los casos, implicaría el fracaso en su resolución (^{Ullauri y Ullauri, 2018}).

Frente a lo planteado, existió la necesidad de analizar las habilidades involucradas en el proceso metacognitivo de los estudiantes de secundaria. En particular, en la asignatura de matemática. Además, se profundizó en las estrategias de aprendizaje que facilitan dicho proceso con el fin comprender el aporte de la metacognición en el aprendizaje de las matemáticas en estudiantes de educación secundaria.

Metodología

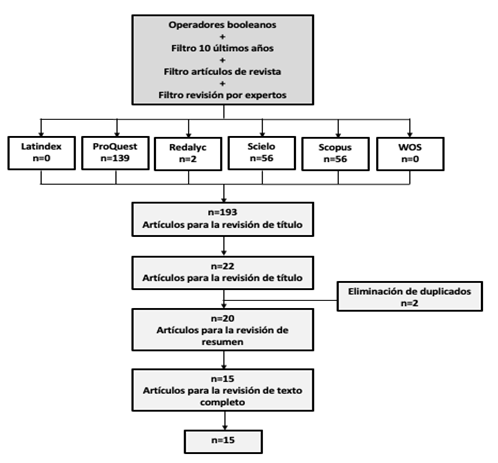
Se realizó una revisión bibliográfica sistemática de 193 artículos publicados en castellano, durante los últimos 11 años en distintas bases de datos (2011-2022) de los cuales se seleccionaron 15 para el análisis. El tema buscado fue la metacognición en matemáticas en estudiantes de secundaria. Los criterios de inclusión utilizados fueron: la temporalidad (últimos 11 años), la fuente (solo revistas científicas) y que fuesen estudios evaluados por expertos. Los 15 artículos seleccionados provienen de las bases de datos ProQuest y Scielo.

La búsqueda se efectuó utilizando las siguientes palabras claves: metacognición, educación secundaria, matemática, en conjunto con sus respectivos sinónimos, lo que fueron conectados a través de los operadores de truncamiento (*, “, (), =, etc.) y booleanos (OR, NOT, AND) originando una ecuación de búsqueda (“Metacognición” OR “Educación secundaria”) AND (“Metacognición” OR “Educación secundaria” OR “Matemática”) AND (“Procesos metacognitivos” OR “matemática”) AND (“Aprender a aprender” OR “Secundaria” OR “Matemática”). Se consideraron solo investigaciones relacionadas con la metacognición en el ámbito de la educación matemática en el nivel de secundaria (equivalente a enseñanza media en Chile). En el caso de las estrategias de aprendizaje, se consideraron las mismas características, aunque no de manera específica a la matemática, sino que en el ámbito educativo general.

Finalmente, los artículos seleccionados se organizaron sobre la base de tres categorías de análisis:

La primera categoría referida a las habilidades metacognitivas en educación matemáticas en secundaria.

La segunda categoría respecto a los procesos metacognitivos en educación matemática en secundaria.

La tercera categoría en relación con las estrategias de aprendizaje en estudiantes de secundaria.

Resultados

A continuación, se presentan los artículos de la muestra seleccionada (Figura 1) y posteriormente se desarrollaron las temáticas de acuerdo con los hallazgos recopilados en los artículos seleccionados.

Figura 1 Proceso de Selección de Artículos Revisados (PRISMA). 

Si bien los artículos seleccionados comprendieron más de una categoría, se destacaron los más representativos para cada una de ellas.

Respecto a las habilidades metacognitivas los autores que asumen esta temática son: ^{Gusmão et al., 2014}; ^{Sánchez et al., 2015}; ^{Tamayo et al., 2018})

Los procesos metacognitivos son abordados por: (^{Gusmão et al., 2014}; ^{Panadero y Alonso, 2014}; ^{Sáiz y Pérez, 2016}; ^{Sánchez et al., 2015}).

Mientras que las estrategias de aprendizaje las analizaron: (^{Maldonado et al., 2019}; Saíz y Pérez, 2016; ^{Suárez et al., 2016}; ^{Torrano et al., 2017})

3.1. Primera categoría: habilidades metacognitivas en educación matemática en secundaria.

Respecto a esta primera categoría, se lograron identificar cuatro investigaciones cualitativas y tres cuantitativas. Estas investigaciones han permitido una comprensión de las habilidades metacognitivas en educación matemática en secundaria por medio de sus propuestas metodológicas con una leve preferencia hacia el tipo de investigación cualitativa.

En relación con las técnicas para recolectar la información y considerando que cada investigación puede abarcar más de una de estas, los artículos revisados en esta primera categoría utilizaron el cuestionario, la entrevista, los grupos focales, la prueba y la revisión bibliográfica. En este sentido, la diferencia fundamental entre prueba y cuestionario radicó en que en la primera (prueba) preguntaba por procesos de la resolución de problemas matemáticos donde la metacognición estaba implícita, a diferencia de la segunda (cuestionario) donde se preguntaba directamente por las habilidades y procesos metacognitivos. Se pudo apreciar que las técnicas que mayormente resaltaron fueron la entrevista, la prueba y la revisión bibliográfica.

En términos prácticos, se pudo evidenciar a través de los artículos que el desarrollo de habilidades metacognitivas y cognitivas juegan un papel importante en el aprendizaje de los estudiantes, donde muchas veces las primeras afectan más en las dificultades y errores en la resolución de tareas matemáticas. Se planteó que ambas son necesarias y debiesen presentarse unidas en el proceso de aprendizaje, dado que el desarrollo de las habilidades cognitivas es previo y necesario para el desarrollo de las habilidades metacognitivas en un segundo momento. El desarrollo de estas se va dando progresivamente junto al desarrollo cognitivo. En este sentido, el hecho de fomentar el aprendizaje activo, constructivo y significativo para cada estudiante potencia el desarrollo de habilidades metacognitivas (^{Gusmão et al., 2014}; ^{Sánchez, 2015}; ^{Sirignano y Magdalena, 2019}; ^{Torres y Sanjosé, 2016}).

Entre las habilidades involucradas en las tareas de matemática por parte de los estudiantes de secundaria destacaron la argumentación, el razonamiento abstracto y la atención sostenida como habilidades cognitivas; además, las funciones ejecutivas como habilidades metacognitivas tales como la planificación, el monitoreo, la evaluación, el control y la flexibilidad mental (^{Gusmão et al., 2014}; ^{Sánchez, 2015}; ^{Tamayo et al., 2018}). Asimismo, ^{Panadero y Alonso (2014}) construyeron un marco comprensivo sobre qué es y cómo hacer para fomentar las habilidades de autorregulación anteriores, explicando estas según distintas teorías y estrategias de aprendizaje enfocadas en educación primaria y secundaria.

Se desprende de la revisión sistemática que las principales habilidades cognitivas y metacognitivas en la enseñanza de la matemática fueron:

Tabla 1 Habilidades Metacognitivas y Cognitivas Presentes en el Aprendizaje de las Matemáticas en Secundaria. 

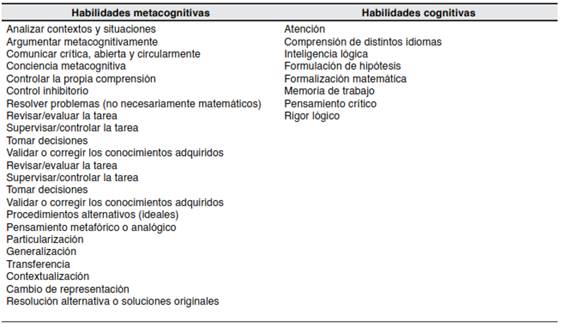
En síntesis, en esta primera categoría se logró observar que potenciar las habilidades metacognitivas permitió un mayor compromiso del aprendiz con la resolución de problemas o tareas y un manejo de habilidades y estrategias (^{Prados et al., 2014}) que les permite razonar y contrastar la información para utilizarla en la vida diaria.

3.3. Tercera categoría: estrategias de aprendizaje en estudiantes secundarios.

En esta tercera categoría, se identificaron dos investigaciones cualitativas y siete cuantitativas, por lo que fue posible asegurar la preferencia hacia el tipo de investigación cuantitativa para el estudio de estrategias de aprendizaje en educación secundaria. Esto se debe a que se aplicaron cuestionarios o escalas que privilegiaron puntuación a través de escalas Likert. Con relación a las técnicas para recolectar la información y considerando que cada investigación puede abarcar más de una de estas, los artículos revisados utilizaron el cuestionario, prueba, revisión bibliográfica y talleres.

La diferencia fundamental entre cuestionario y prueba radicó en que en la primera (cuestionario) preguntaba directamente por estrategias de aprendizaje, a diferencia de la segunda (prueba) que preguntaba por procesos de la resolución de problemas matemáticos donde las estrategias de aprendizaje estaban implícitas, destacándose en mayor medida el cuestionario, en contraste con la prueba, la revisión bibliográfica y los talleres. De este modo, los artículos destacaron la importancia de incorporar la metacognición y las estrategias de aprendizaje en conjunto, no tan solo en la teoría, sino también en la práctica; de manera que los objetivos de aprendizaje giren en torno a estrategias que fomenten la planificación y autoevaluación de las tareas de aprendizaje, adoptando así una posición crítica frente al propio proceso de aprendizaje (^{Arteaga et al., 2020}; Saíz y Pérez, 2016; ^{Suárez et al., 2016}; ^{Torrano et al., 2017}).

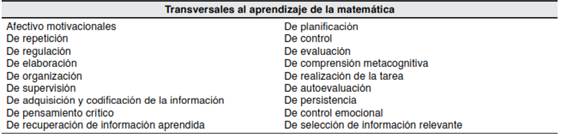
Los autores revisados sostuvieron que existen estrategias transversales al aprendizaje que facilitan el desarrollo de otras específicas para la matemática, estas fueron:

Tabla 2 Estrategias de Aprendizaje Cognitivas y Metacognitivas. 

En general, se concluyó que se deben adoptar estrategias de aprendizaje enfocadas tanto en procesos metacognitivos como cognitivos (Saíz y Pérez, 2016; ^{Suárez et al., 2016}; ^{Torrano et al., 2017}). En específico, para las primeras se mostró un efecto positivo en el aprendizaje cuando se refieren a la autorregulación y motivación, puesto que permite gestionar y mejorar el propio aprendizaje y al mismo tiempo la motivación (^{Cerda y Vera, 2019}; Suárez et al., 2016).

Igualmente, ^{Maldonado et al. (2019}) concluyeron que la estrategia de codificación de información impactó en mayor medida en la autonomía de los estudiantes. También, ^{Solano et al. (2016}) identificaron que en los lectores hábiles predominaban estrategias de aprendizaje y procesos metacognitivos, a diferencia de los estudiantes que no fueron lectores hábiles, por tanto, se consideró la comprensión lectora tanto en lengua castellana como en matemática.

^{Cerda y Vera (2019}) se orientaron específicamente al área de matemática deduciendo que las estrategias basadas en habilidades cognitivas, motivacional- afectivas y de autorregulación, se relacionaron de manera positiva con el rendimiento académico en la asignatura. Paralelamente, ^{Arteaga et al. (2020}), mostraron la importancia de la regulación cognitiva en la resolución de problemas verbales matemáticos, sugiriendo éstos como un recurso exploratorio de las estrategias metacognitivas que el estudiante debe poner en funcionamiento y que le sirven de información para adaptarse a la metodología que utiliza el profesor en el aula. En síntesis, los autores concordaron que existió una correlación positiva entre el uso de estrategias de aprendizaje en el rendimiento académico y la calidad del aprendizaje (Arteaga et al., 2020; Cerda y Vera, 2019; Saíz y Pérez, 2016; ^{Solano et al., 2016}; ^{Suárez et al., 2016}; ^{Valencia y Caicedo, 2015}).

Conclusiones

Tal como lo reflejó la evidencia empírica de los artículos revisados, la metacognición no ha sido un elemento aislado dentro del aprendizaje, y el aprendizaje de la matemática en secundaria no ha sido la excepción. Así, ha resultado necesario que esta se manifieste en armonía con los elementos cognitivos; ya que alguna carencia en alguna de estas dos configuraciones (metacognitiva y cognitiva) ha implicado el desarrollo ineficaz de la tarea. Por ende, un aprendizaje significativo en los estudiantes, independiente del área de estudio, está estrechamente ligado con procesos de aprendizaje donde se incluyan habilidades metacognitivas y estrategias de aprendizaje (^{Arteaga et al., 2020}; ^{Cerda y Vera, 2019}; ^{Dorado et al., 2020}; ^{Gusmão et al., 2014}; ^{Maldonado et al., 2019}; ^{Sáiz y Pérez, 2016}; ^{Panadero y Alonso, 2014}; ^{Sánchez et al., 2015}; ^{Sirignano y Magdalena, 2019}; ^{Solano et al., 2016}; ^{Suárez et al., 2016}; ^{Tamayo et al., 2018}; ^{Torres y Sanjosé, 2016}; ^{Torrano et al., 2017}; ^{Valencia y Caicedo, 2015}).

En este sentido, la estimulación de la actividad cognitiva en educación matemática en secundaria, depende de cómo los docentes posibiliten la metacognición, desde metodologías de enseñanza que motiven a los aprendices a desarrollar para poner en práctica la autorreflexión, la creatividad, la solución de problemas, así como poner en práctica funciones ejecutivas que les permitan procesos como el planificar, organizar, guiar, revisar, regularizar y evaluar su propio proceso de aprendizaje (^{Cerda y Vera, 2019}; ^{Gusmão et al., 2014}; ^{Sáiz y Pérez, 2016}; ^{Panadero y Alonso, 2014}; ^{Sánchez et al., 2015}; ^{Sirignano y Magdalena, 2019}; ^{Tamayo et al., 2018}; ^{Torres y Sanjosé, 2016}).

En específico, las estrategias de aprendizaje han tenido importantes implicaciones en el ámbito psicoeducativo justificando la necesidad de ser incluidas en los modelos de enseñanza y aprendizaje para desarrollar técnicas y estrategias específicas que mejoren aspectos como la comprensión y argumentación metacognitiva, aspectos afectivo- motivacionales y funciones ejecutivas. En consecuencia, que los estudiantes de secundaria determinen situaciones de creación, mantenimiento y evaluación de tareas, así como de flexibilidad, control mental, planificación y autonomía (^{Arteaga et al., 2020}; ^{Cerda y Vera, 2019}; ^{Dorado et al., 2020}; ^{Maldonado et al., 2019}; ^{Sáiz y Pérez, 2016}; ^{Solano et al., 2016}; ^{Suárez et al., 2016}; ^{Torrano et al., 2017}; ^{Valencia y Caicedo, 2015}).

Para incorporar la metacognición efectivamente en el aula se hace necesario una adecuación en la formación de estudiantes de pedagogía, que les permita tener una visión amplia de distintas teorías y modelos de enseñanza que faciliten la comprensión de todos los procesos cognitivos y metacognitivos que los estudiantes de secundaria activan y desarrollan durante los procesos de enseñanza y aprendizaje. Lo anterior permitiría una mayor comprensión teórica profunda de la implementación de distintas estrategias de aprendizaje de los futuros docentes para lograr las metas de aprendizaje que los programas educativos diseñan en los distintos niveles de educación secundaria. Por otra parte, los docentes deben mediar para que los aprendices adquieran y desarrollen habilidades y competencias requeridas en la educación contemporánea.

Antes de enseñar tales estrategias, es necesario que los estudiantes de pedagogía y los docentes las utilicen en beneficio de su propio aprendizaje, lo que permitirá una comprensión y consciencia profunda acerca de éstas facilitando su implementación eficaz en el aula.

Con relación a lo mencionado anteriormente, la reflexión pedagógica ha cobrado vital importancia al permitir a cada docente pensar acerca de su propia práctica, evaluando si la metodología considera las necesidades del alumnado de manera integral, y que permita que cada estudiante logre adquirir y poner en práctica estrategias de aprendizaje para las tareas de aprendizaje requeridas, junto con el desarrollo de habilidades metacognitivas. Al mismo tiempo, ha sido primordial en la formación continua como docentes mirar en retrospectiva, donde cuyo punto de reflexión sea el pilar la educación, es decir, la formación y el crecimiento individual de los estudiantes como personas y futuros ciudadanos, quienes se tendrán que enfrentar con la cambiante realidad moderna, que les exige habilidades más complejas y les presenta retos de escenarios desconocidos y nuevos.

Ahora bien, el desafío como educadores, en matemáticas y otras asignaturas, no es proponer tareas o problemas creados por otros en contextos no congruentes con los que se pensaron, sino que el reformular y/o crear enunciados y tareas para ser adaptados al aula en cuestión, respecto a características individuales y grupales, así como de factores internos y externos al aprendizaje. Sin embargo, no de manera aislada a las configuraciones metacognitivas que la propia cognición requiere casi naturalmente.

Considerando el ámbito nacional, ha sido posible afirmar la casi inexistente investigación respecto a la metacognición en matemáticas en estudiantes de secundaria. Donde solo un artículo revisado fue desarrollado en Chile, con una muestra muy concreta que no permitió generalizar, encontrar razones robustas o soluciones respecto al tema. Una realidad que ha preocupado considerando los bajos niveles en la asignatura de matemática según pruebas estandarizadas a nivel mundial y que, al mismo tiempo, no concuerda con lo estipulado en los distintos documentos que guían la educación chilena. Dentro de los cuales están involucradas las habilidades para el siglo XXI, siendo la metacognición una habilidad fundamental y transversal al aprendizaje en los estudiantes, pero también una competencia necesaria como futuros ciudadanos.