Introducción
En 2022 el hormigón fue el principal material de construcción para cimientos y estructuras en todo el Ecuador (Instituto nacional de estadísticas, 2022). Por su importancia y uso masivo, es un material que debe ser idealizado correctamente al momento de diseñar estructuras. Dos parámetros fundamentales para el diseño de las estructuras de hormigón son la resistencia a la compresión (𝑓’𝑐), y el módulo de elasticidad. Con base a la filosofía del diseño estructural estos parámetros son considerados por normativas nacionales e internacionales para el diseño de elementos estructurales tales como vigas, columnas, muros, cimientos, entre otros, además están correlacionados entre sí, donde se utiliza la resistencia a la compresión para la determinación del módulo de elasticidad por medio de ecuaciones establecidas en base a resultados de ensayos y métodos estadísticos (American Concrete Institute (ACI), 2019).
Un total de seis estudios (Herrería y Villegas, 2008), (Asmal, et al 2012), (García, 2013), (Laboratorio de ensayo de materiales y modelos. Carrera de Ingeniería Civil. UCE, 2013), (Alejandro, 2014), (Paucar y Sacasari, 2017), la normativa nacional NEC 15 y la normativa internacional ACI318 se realizaron para la determinación del módulo de elasticidad del hormigón en el Ecuador, tomando en cuenta variables como resistencia a la compresión, procedencia del agregado, tipo de cemento, elaboración del hormigón, entre otros, demostrando que la ecuación convencionalmente utilizada y normada, no es cercana a la realidad, y proponiendo varias ecuaciones alternativas. Estas ecuaciones alternativas a su vez varían unas de otras, por las características particulares de cada estudio.
A continuación, se presentan las ecuaciones obtenidas de códigos de diseño y las más representativas de diversas investigaciones realizadas para determinar el módulo de elasticidad en Ecuador. Se destaca que, en todos estos estudios, el módulo de elasticidad se relaciona con la resistencia a la compresión, sin considerar la procedencia del agregado, el tipo de cemento ni el proceso de producción. Además, se debe mencionar que la principal limitación de estos estudios es que, para cada sitio específico o cambio en el tipo de cemento o proceso de producción, la ecuación varía, lo que impide estimar datos nuevos de módulo de elasticidad fuera de su zona de estudio.
ACI 318/NEC 15 Ec=4700√(f´c) (1)
ESPE (Herrería y Villegas, 2008) Ec=3440√(f´c) (2)
UCE (Asmal, et al 2012) Ec=3980√(f´c) (3)
UCE (García, 2013) Ec=3246√(f´c) (4)
UCE 8
Ec=2937√(f´c) (5)
EPN (Alejandro, 2014) Ec=3875√(f´c) (6)
UCE (Paucar y Sacasari , 2017) Ec=3075√(f´c) (7)
Las ecuaciones anteriores se han tomado como referencia de los estudios realizados, pero muchos de ellos presentan más de una ecuación debido a que la relación entre el módulo de elasticidad y sus variables asociadas puede cambiar según factores como la producción, la procedencia del agregado y el tipo de cemento. Estas variaciones en las ecuaciones reflejan la complejidad del comportamiento del hormigón y la necesidad de considerar múltiples factores para la obtención del módulo de elasticidad.
Además, se puede observar que no existe una ecuación única y la variación de los estudios respecto a las normativas de diseño es significativa. Entre las ecuaciones obtenidas de estudios previos también se presenta una variación notable. La incertidumbre sobre qué ecuación utilizar recae en diseñadores o investigadores, quienes deben seleccionar la más adecuada según sus necesidades particulares.
También se ha desarrollado un método de predicción utilizando redes neuronales (Machado et al., 2024), el cual considera variables de entrada como densidades de materiales, módulos de finura y capacidad de absorción, entre otras. Si bien estas variables son útiles para los investigadores, pueden resultar algo complicadas para los productores, diseñadores y constructores.
Dentro del diseño de las estructuras el módulo de elasticidad es un hito clave para la determinación de deformaciones y desplazamientos, así como también la obtención de fuerzas sísmicas, rigidez lateral de piso, y el cálculo de derivas de piso en una estructura. Es aquí donde radica la importancia de la correcta idealización del módulo de elasticidad.
Tomando en cuenta que la predicción del módulo de elasticidad se calcula como un aproximado, es factible implementar la teoría de la lógica difusa para su determinación. Esta teoría, aplicada en ingeniería, considera la tolerancia y la imprecisión que son aplicables al módulo de elasticidad. Se emplean Sistemas de Inferencia Lógica (SIL), los cuales son funciones universales no lineales aproximadas que pueden predecir nuevos datos a partir de un entrenamiento previo (Ross, 2010).
El principal objetivo de la presente investigación es desarrollar un modelo que permita estimar el módulo de elasticidad utilizando la teoría de lógica difusa, mediante un sistema de inferencia lógico ANFIS (Adaptive Neuro Fuzzy Inference Systems). Para ello, se empleará la experiencia previamente obtenida a partir de ensayos de laboratorio, que incluyen un total de 132 ensayos. Las variables introducidas en el modelo serán el sitio de producción, el origen del agregado, el tipo de cemento, la edad de ensayo, la resistencia a la compresión y el propio módulo de elasticidad. Estos datos constituyen el conocimiento previo que permitirá crear funciones de membresía (FMs) y reglas difusas del tipo condicional (If-Then) para estimar o predecir nuevos datos del módulo de elasticidad. De esta manera, la variable de entrada no se limitará únicamente a la resistencia a la compresión, sino que contemplará otras variables importantes en el proceso de determinación del módulo de elasticidad.
Metodología
A continuación, se muestra el proceso utilizado para desarrollar un modelo que pueda estimar el módulo de elasticidad usando la teoría de la lógica difusa. Figura 1.
Obtención de datos
El primer paso es la obtención de datos de estudio que sean relevantes y permitan desarrollar la presente investigación. Para ello, se ha realizado una revisión de seis distintas tesis de grado realizadas por diferentes universidades del país. Estas tesis proporcionaron ecuaciones que relacionan el módulo de elasticidad con la resistencia a la compresión del hormigón. Sin embargo, se observa que, si bien estas investigaciones tomaron en cuenta características singulares para determinar el módulo de elasticidad, al estimarlo solo se consideró la relación existente con la resistencia a la compresión del hormigón. Es importante señalar que las características de estas investigaciones previas incluyen la procedencia del agregado, el tipo de cemento, la edad de ensayo, la resistencia a la compresión y el sitio/proceso de producción. Se reconoce que todas estas variables influyen en los resultados de la obtención del módulo de elasticidad, no solo la resistencia a la compresión.
Por lo tanto, en esta investigación se involucrarán cinco variables de entrada, a saber:
Variable 1: Sitio de producción, tres diferentes sitios. Unidad sitio.
Variable 2: Origen del agregado, dos diferentes canteras. Unidad cantera.
Variable 3: Tipo de cemento, dos tipos de cemento. Unidad tipo.
Variable 4: Edad de ensayo, tres edades diferentes. Unidad días.
Variable 5: Resistencia a la compresión (f´c), la característica de cada probeta. Unidad MPa.
La variable de salida o la variable objetivo variable 6 será el módulo de elasticidad. Unidad MPa.
En la Tabla 1, se resumen las seis investigaciones en análisis, su tema, las características principales que se tomaron en cuenta en el desarrollo de cada una y la relación con las cinco variables de esta investigación.
Tabla 1: Investigaciones previas y sus variables
| INVESTIGACIÓN | PROCEDENCIA DEL AGREGADO | TIPO DE CEMENTO | EDAD DE ENSAYO | RESISTENCIA A LA COMPRESIÓN | PROCESO DE PRODUCCIÓN. |
|---|---|---|---|---|---|
| “Módulos de elasticidad y curvas de esfuerzo deformación, en base a la compresión del hormigón a 21, 28, 35 MPa”, (Herrería y Villegas, 2008) | x | x | |||
| “Estudio del módulo de elasticidad estático del hormigón en base a la resistencia a la compresión (f´c= 21, 28 Mpa) fabricado con material de la mina de Pintag.” (Asmal, et al 2012) | x | x | x | ||
| “Módulo de elasticidad estático del hormigón para varios tipos de agregados” (Laboratorio de ensayo de materiales y modelos, Carrera de Ingeniería Civil, UCE 2013) | x | x | x | ||
| “Módulo estático de elasticidad del hormigón en base a su resistencia a la compresión (f’c = 24MPa), fabricado con materiales de la mina Villacres, ubicada en el sector de la Península Cantón Ambato en la Provincia de Tungurahua y cemento holcim.”, (García, 2013) | x | x | x | x | |
| “Módulo de elasticidad de hormigones de peso normal empleados en el Ecuador f´c: 21, 24, 28,35 MPa” (Alejandro, 2014) | x | x | x | x | x |
| “Caracterización del módulo estático de elasticidad del hormigón a partir de pruebas a compresión simple en probetas cilíndricas con diferentes agregados del cantón quito, provincia de Pichincha” (Paucar y Sacasari, 2017) | x | x | x |
Como se observa en la Tabla 1, la tesis de Alejandro (2014) abarca todas las variables que se involucran en la presente investigación. Estos datos serán utilizados para el entrenamiento, chequeo y validación del Sistema de Inferencia Lógico (SIL) con teoría de lógica difusa. Es importante destacar que, para la variable 1 (Sitio de producción), solo esta tesis la considera debido a que fue realizada con datos reales de campo, en contraste con ensayos controlados de laboratorio que se utilizaron en los otros estudios. Esta diferencia en la fuente de datos confiere a la tesis de Alejandro (2014) un valor significativo para esta investigación.
Generación del Sistema de inferencia lógico (SIL)
Para la modelación difusa se generó automáticamente un sistema de inferencia lógico (SIL) tipo Sugeno permitiendo una identificación del sistema utilizando las variables de entrada y salida que fueron escogidas previamente.
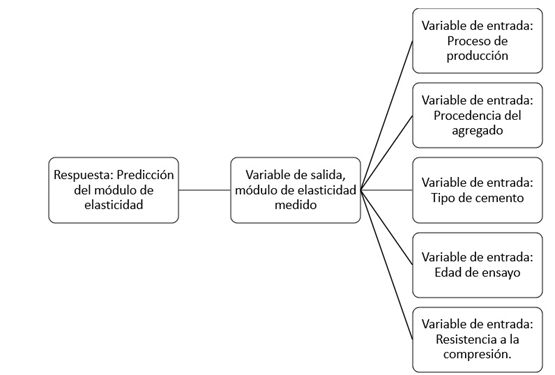
La generación del sistema de inferencia lógico o modelo difuso, parte del conocimiento previo en este caso los resultados de investigaciones precedentes (Alejandro, 2014) donde se identificaron las variables de entrada y salida (Figura 2):
Variables de entrada
Sitio/proceso de producción (V1)
Procedencia del agregado (V2)
Tipo de cemento (V3)
Edad de ensayo (V4)
Resistencia a la compresión (V5)
Variables de salida
Módulo de elasticidad (V6)
El sistema de inferencia lógico (SIL) requiere un entrenamiento y un chequeo con variables conocidas. De los datos totales escogidos para esta investigación, el 70% son utilizados para el entrenamiento y el 30% para el chequeo.
Se escoge entre los mecanismos de inferencia lógica el tipo Sugeno, ya que este produce resultados con valores discretos, es decir valores no difusos (Takagi y Sugeno, 1985).
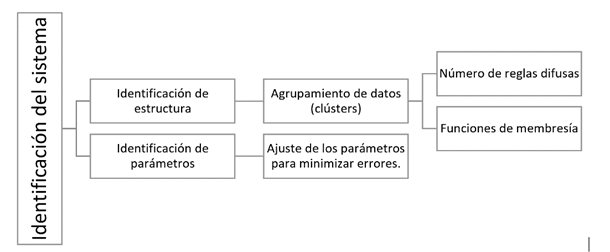
La identificación del sistema desarrolla la estructura mediante el agrupamiento de datos (clústeres), que le permite determinar el número de reglas difusas y funciones de membresía para el sistema, esto se desarrolla por medio del método de agrupamiento sustractivo (Chiu, 1994). Además, seguidamente se identifica parámetros para ajustarlos y minimizar errores. Figura 3.
Se asignan los grados de membresía a los datos de entrada mediante la utilización de las funciones de membresía (FMs). A partir de estos datos, se generan las reglas difusas que relacionan las variables consideradas (Takagi y Sugeno, 1985).
Al utilizar el método de agrupamiento sustractivo, para el sistema de inferencia lógico tipo Sugeno se utilizan las funciones de membresía tipo gaussianas para obtener un valor discreto no difuso, este será el módulo de elasticidad que se puede obtener a partir de las variables de entrada consideradas para el desarrollo del presente modelo.
Con datos que no se utilizaron ni para el entrenamiento ni para el chequeo del sistema de inferencia lógico, se realiza la validación del modelo. Con estos datos se puede verificar si el modelo puede estimar el módulo de elasticidad del hormigón considerando todas las variables de entrada para nuevos valores de estas.
Resultados
Se seleccionaron 132 datos que involucran todas las variables. De estos datos se escogieron aleatoriamente 118 para entrenamiento y chequeo. El sistema de inferencia lógico fue entrenado con 83 datos, correspondiente al 70% de la muestra, a continuación, para el chequeo del SIL de utilizó 35 datos, correspondiente al 30% de la muestra. Para la validación se utilizaron 14 datos restantes.
El método de agrupamiento sustractivo ha utilizado los siguientes parámetros en el desarrollo del SIL:
Relación de aceptación=0.5
Relación de rechazo=0.15
Rango de influencia=0.5
Factor squash=1.5
El sistema de inferencia lógico (SIL) realizó el agrupamiento de datos en 17 clústeres, además seleccionó las funciones de membresía (FMs) en un total de cinco, que se corresponden con las variables de entrada (origen del agregado, tipo de cemento, sitio/proceso de producción, edad de ensayo, resistencia a la compresión).
Con el agrupamiento sustractivo de datos se generaron 17 reglas difusas, relacionando las variables de entrada. Las 17 reglas difusas son:
Si (V1 está en Clúster 1) y (V2 está en Clúster 1) y (V3 está en Clúster 1) y (V4 está en Clúster 1) y (V5 está en Clúster 1) entonces (V6 está en Clúster 1)
Si (V1 está en Clúster 2) y (V2 está en Clúster 2) y (V3 está en Clúster 2) y (V4 está en Clúster 2) y (V5 está en Clúster 2) entonces (V6 está en Clúster 2)
Si (V1 está en Clúster 3) y (V2 está en Clúster 3) y (V3 está en Clúster 3) y (V4 está en Clúster 3) y (V5 está en Clúster 3) entonces (V6 está en Clúster 3)
Si (V1 está en Clúster 4) y (V2 está en Clúster 4) y (V3 está en Clúster 4) y (V4 está en Clúster 4) y (V5 está en Clúster 4) entonces (V6 está en Clúster 4)
Si (V1 está en Clúster 5) y (V2 está en Clúster 5) y (V3 está en Clúster 5) y (V4 está en Clúster 5) y (V5 está en Clúster 5) entonces (V6 está en Clúster 5)
Si (V1 está en Clúster 6) y (V2 está en Clúster 6) y (V3 está en Clúster 6) y (V4 está en Clúster 6) y (V5 está en Clúster 6) entonces (V6 está en Clúster 6)
Si (V1 está en Clúster 7) y (V2 está en Clúster 7) y (V3 está en Clúster 7) y (V4 está en Clúster 7) y (V5 está en Clúster 7) entonces (V6 está en Clúster 7)
Si (V1 está en Clúster 8) y (V2 está en Clúster 8) y (V3 está en Clúster 8) y (V4 está en Clúster 8) y (V5 está en Clúster 8) entonces (V6 está en Clúster 8)
Si (V1 está en Clúster 9) y (V2 está en Clúster 9) y (V3 está en Clúster 9) y (V4 está en Clúster 9) y (V5 está en Clúster 9) entonces (V6 está en Clúster 9)
Si (V1 está en Clúster 10) y (V2 está en Clúster 10) y (V3 está en Clúster 10) y (V4 está en Clúster 10) y (V5 está en Clúster 10) entonces (V6 está en Clúster 10)
Si (V1 está en Clúster 11) y (V2 está en Clúster 11) y (V3 está en Clúster 11) y (V4 está en Clúster 11) y (V5 está en Clúster 11) entonces (V6 está en Clúster 11)
Si (V1 está en Clúster 12) y (V2 está en Clúster 12) y (V3 está en Clúster 12) y (V4 está en Clúster 12) y (V5 está en Clúster 12) entonces (V6 está en Clúster 12)
Si (V1 está en Clúster 13) y (V2 está en Clúster 13) y (V3 está en Clúster 13) y (V4 está en Clúster 13) y (V5 está en Clúster 13) entonces (V6 está en Clúster 13)
Si (V1 está en Clúster 14) y (V2 está en Clúster 14) y (V3 está en Clúster 14) y (V4 está en Clúster 14) y (V5 está en Clúster 14) entonces (V6 está en Clúster 14)
Si (V1 está en Clúster 15) y (V2 está en Clúster 15) y (V3 está en Clúster 15) y (V4 está en Clúster 15) y (V5 está en Clúster 15) entonces (V6 está en Clúster 15)
Si (V1 está en Clúster 16) y (V2 está en Clúster 16) y (V3 está en Clúster 16) y (V4 está en Clúster 16) y (V5 está en Clúster 16) entonces (V6 está en Clúster 16)
Si (V1 está en Clúster 17) y (V2 está en Clúster 17) y (V3 está en Clúster 17) y (V4 está en Clúster 17) y (V5 está en Clúster 17) entonces (V6 está en Clúster 17)
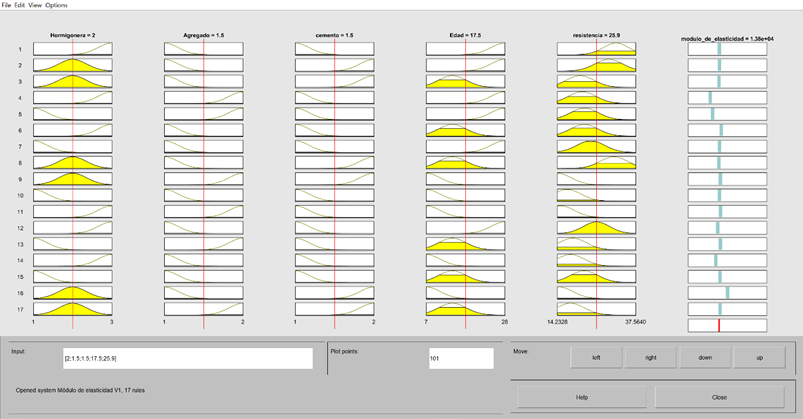
El sistema de inferencia lógico (SIL), utilizó el método de agrupamiento sustractivo tipo Sugeno con las funciones de membresía tipo gaussianas para obtener un valor discreto no difuso, este valor encontrado corresponde al módulo de elasticidad, cuya obtención es el objetivo de esta investigación, este módulo de elasticidad, no relaciona solamente la resistencia a la compresión como en el caso convencional de los códigos y normativas de diseño, sino que toma en cuenta las cinco variables de entrada, permitiendo así tener un acercamiento más real, al módulo de elasticidad de hormigón. Figura 4.
Para validar el modelo se utilizaron datos nuevos que no se usaron ni para el entrenamiento ni para el chequeó del modelo, estos datos se seleccionaron al azar donde todas las variables de entrada y salida se involucran.
En la Tabla 2, se muestran los datos para verificación donde se encuentran las 5 variables utilizadas en las columnas C1 a la C5, La columna C6 indica el módulo de elasticidad medido en laboratorio, la columna C7, indica el valor obtenido mediante el modelo desarrollado por el SIL, la columna C8 indica el valor del módulo de elasticidad obtenido mediante la ecuación sugerida en (Alejandro, 2014), la columna C9 indica el error obtenido mediante la utilización del SIL, y finalmente la columna C10 indica el error obtenido por la utilización de la ecuación.
Tabla 2: Datos para validación de modelo y comparativa de error del SIL y Ecuación
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | Ec (Mpa) | SIL Ec (Mpa) | Ecuación Ec (Mpa) | Error SIL | Error Ecuación |
| 1 | 2 | 1 | 7 | 14.28 | 9360.71101 | 10200 | 14628.401 | -8% | -36% |
| 2 | 2 | 2 | 7 | 14.23 | 10491.5748 | 10500 | 14524.6639 | 0% | -28% |
| 1 | 1 | 1 | 14 | 25.68 | 17432.6308 | 17000 | 19613.8959 | 3% | -11% |
| 1 | 2 | 1 | 28 | 22.76 | 19003.1697 | 17100 | 18465.4303 | 11% | 3% |
| 1 | 1 | 1 | 28 | 24.48 | 18696.5566 | 18700 | 19148.2047 | 0% | -2% |
| 1 | 1 | 1 | 28 | 29.09 | 21676.2189 | 20200 | 20875.21 | 7% | 4% |
| 2 | 1 | 2 | 7 | 24.72 | 13780.1038 | 12800 | 19144.3401 | 8% | -28% |
| 2 | 1 | 2 | 14 | 30.96 | 17143.7098 | 18400 | 21422.2866 | -7% | -20% |
| 2 | 2 | 2 | 28 | 21.39 | 17525.1914 | 20200 | 17807.238 | -13% | -2% |
| 2 | 1 | 2 | 28 | 28.19 | 20369.1276 | 20200 | 20442.8168 | 1% | 0% |
| 3 | 1 | 1 | 14 | 22.43 | 13648.5851 | 15500 | 18494.7114 | -12% | -26% |
| 3 | 1 | 1 | 28 | 33.21 | 18006.3473 | 23700 | 22504.6219 | -24% | -20% |
| 3 | 1 | 1 | 28 | 28.06 | 19675.1637 | 19800 | 20685.6026 | -1% | -5% |
| 3 | 1 | 1 | 28 | 26.08 | 19390.1743 | 18300 | 19942.8397 | 6% | -3% |
| Desviación estándar | 0.097 | 0.134 | |||||||
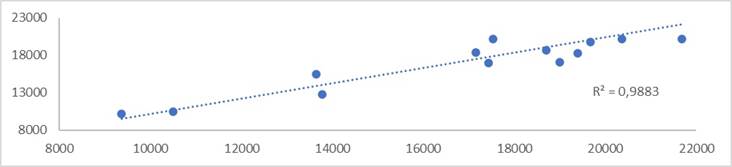
El proceso de validación del modelo, para medir la precisión general de este, se realizó con el coeficiente R2=0.98. Figura 5. La desviación estándar se usó para medir la dispersión de los datos utilizados, comparada con la obtenida con la ecuación de (Alejandro, 2014).
En la Figura 5, se muestran en el eje “x” los valores obtenidos mediante ensayos de laboratorio de módulo de elasticidad en MPa (Columna 6); en el eje “y” los valores calculados de módulo de elasticidad en MPa para las cinco variables de entrada, con el sistema de inferencia lógico SIL para los datos de la validación (Columna 7).
Discusión
Como se observa en la Figura 4, el sistema de inferencia lógico SIL, desarrolló el modelo capaz de predecir el módulo de elasticidad partiendo de 17 reglas difusas gaussianas que relacionan las cinco variables de entrada, y devolviendo un valor discreto que es la variable de salida módulo de elasticidad.
En el apartado validación del modelo, Tabla 2 se puede observar como el sistema de inferencia lógico SIL (Columna 7) predice el módulo de elasticidad, y al ser comparados con el módulo de elasticidad real tomado de laboratorio (Columna 6) se puede construir la Figura 5 obteniendo un coeficiente de correlación R2 de 0.98 el cual es un valor muy alto y es un indicativo de la predicción eficiente que se consigue mediante el modelo desarrollado por el sistema de inferencia lógico SIL.
En la Tabla 2 además se encontró resultados del módulo de elasticidad obtenido mediante la ecuación que se sugiere en la investigación de (Alejandro, 2014), (Columna 8). Con los datos obtenidos del SIL y de la ecuación, (columna 9 y 10) se encontró la variación que se calculan con relación al módulo de elasticidad real (columna 6), se observa que, para el modelo del SIL, 4 valores de los analizados superan el 10% de error, mientras que para el caso de la ecuación son 7 los valores que superan el 10% de error. Estos resultados se pueden verificar además mediante la desviación estándar que, para el caso del modelo desarrollado por el SIL es de 0.097, mientras que para el caso de la ecuación es del 0.134.
En la investigación tomada de base, el autor ha desarrollado una ecuación para cada sitio donde se realiza el proceso de producción del hormigón, en total existen tres sitios de producción del hormigón, el sitio 1 responde a la ecuación E=3870raíz(f´c), el sitio 2 responde a la ecuación E=3850raíz(f´c), el sitio 3 responde a la ecuación E=3905raíz(f´c) (Variable 1), para que estas sean más cercanas a la realidad, es decir no se puede utilizar una única ecuación que satisfaga el cálculo del módulo de elasticidad del hormigón, mientras que el SIL es capaz de desarrollar un modelo único que permite la entrada de todas las variables que influencien en la determinación del módulo de elasticidad y devolver valores confiables.
Conclusiones
Por medio de la identificación del sistema, con ayuda de datos de entrada reales se genera un sistema de inferencia lógica tipo Sugeno de forma automatizada, el proceso se vuelve sencillo y amigable con el usuario, volviendo al modelo desarrollado una solución practica para ser implementada por productores de hormigón, laboratoristas, diseñadores o investigadores, que deseen estimar el módulo de elasticidad por medio de conocimiento previo del tema y sin necesidad de hacerlo por el método convencional.
Utilizando la teoría de lógica difusa, se desarrolló un modelo que permite estimar el módulo de elasticidad, por medio de un sistema de inferencia lógico ANFIS (Adaptive Neuro Fuzzy Inference Systems), partiendo de la experiencia previa obtenida de ensayos de laboratorio y utilizando variables fundamentales que lo influencian como el sitio/proceso de producción, el origen del agregado, el tipo de cemento, la edad de ensayo, la resistencia a la compresión y el módulo de elasticidad. El modelo al ser abarcador y considerar variables de entrada más no sólo la resistencia a la compresión es capaz de estimar adecuadamente el módulo de elasticidad.
Las cinco variables de entrada utilizadas en esta investigación se limitan a los datos del estudio de (Alejandro, 2014) con dos datos de procedencia del agregado, dos tipos de cemento, tres sitios de producción, tres edades de ensayo, y la resistencia a la compresión característica de cada cilindro de prueba (132). Estas variables podrían aumentar a fin de generar un modelo más amplio y adecuado a la utilización del usuario final, sea este investigador o diseñador.
Las investigaciones que preceden a esta han desarrollado una ecuación para cada condición específica de las variables de entrada, y esa ecuación sólo es adaptable a esas condiciones, mientras que el modelo desarrollado para estimar el módulo de elasticidad permite estimarlo con la ayuda de un único modelo que se adapte al cambio de cualquiera de las variables de entrada, y devolviendo un valor de módulo de elasticidad confiable y útil para el diseño de las estructuras.
Además de las cinco variables que influyen directamente en la estimación del módulo de elasticidad del hormigón, estudiadas en la presente investigación, si se necesitan implementar más variables como proceso de mezclado, densidades de materiales, entre otros, es posible mediante la teoría de la lógica difusa, por medio del sistema de inferencia lógico.