INTRODUCCIÓN
En Perú, un estudiante universitario de pregrado es aquel que ha concluido sus estudios de educación secundaria, ha aprobado el proceso de admisión a una universidad, ha alcanzado vacante y se encuentra matriculado en ella. Así, la Universidad Nacional Agraria La Molina de Lima, Perú (UNALM), es una institución educativa que brinda formación en 12 carreras universitarias de pregrado relacionadas al uso y gestión de recursos agropecuarios y la conservación del medio ambiente, organiza procesos de admisión semestrales, mediante los cuales los postulantes buscan alcanzar una vacante para acceder a los estudios universitarios, a través de la resolución de un examen que mide sus conocimientos.
El proceso de admisión se puede dividir en tres etapas: inscripción, examen y asignación de vacantes. En la etapa de inscripción, el postulante, además de brindar sus datos entre los que se encuentra la modalidad de ingreso, la cual se define según los requisitos que el postulante cumple, siendo las más comunes la de concurso ordinario, centro preuniversitario (CEPRE), primer y segundo puesto de colegio, y quinto de secundaria.
La segunda etapa consiste en el examen de admisión, el cual está compuesto preguntas concernientes a las áreas de Razonamiento matemático, Razonamiento Verbal, Matemática, Física, Química y Biología. Sin embargo, existen excepciones en cuanto a los postulantes de algunas modalidades quienes rinden un examen distinto: Traslados Externos y Graduados y Titulados y CEPRE. Finalmente, el proceso de asignación de vacantes se realiza en estricto orden de mérito para cada una de las modalidades del proceso de admisión, es decir aquellos que optaron por distintas modalidades no compiten por una misma vacante.
Luego de haber conseguido una vacante, el ingresante confirma su incorporación a la UNALM realizando su matrícula del primer semestre. En su condición de alumno matriculado y en función a su rendimiento académico, se le adjudica una de las siguientes situaciones académicas: Normal, Observado, Suspendido, Prueba o Separado. La situación Normal es asignada automáticamente a los estudiantes de primer año (dos primeros semestres) y a aquellos que mantienen su promedio semestral en un valor mayor o igual a 11. Las demás situaciones académicas comienzan a regir a partir del tercer semestre. Así, un estudiante es Observado si su último promedio semestral es inferior a 11, y es Suspendido si sus 2 últimos promedios semestrales son inferiores a 11, lo cual le imposibilita la matrícula en el semestre académico siguiente. Luego de subsanar una observación, la situación académica futura puede volver a ser Normal, sin embargo, esto sucede después de subsanar una suspensión, su condición pasaría a ser Normal con antecedente. Finalmente, la situación de Prueba es aquella que presenta el estudiante que se matricula luego de una suspensión. Si en esta situación, vuelve a reportar un promedio semestral inferior de 11, pasa automáticamente a la situación de Separación académica, con la cual pierde la condición de estudiante de la UNALM.
En la literatura se pueden encontrar diversos estudios acerca del rendimiento académico en estudiantes universitarios. En el estudio llevado a cabo por Gómez-Sánchez, Martínez-López, Oviedo-Marín10 se encontró que el sexo del estudiante y el semestre de estudios, así como su promedio y satisfacción con la carrera influyen en su desempeño académico. Por otro lado, Ocaña22, en su investigación, lista un conjunto de potenciales variables académicas que tienen repercusión en el rendimiento académico, entre las que menciona las características del colegio de procedencia, el rendimiento en las pruebas de admisión, el desempeño universitario en el año previo al del estudio, la vocación, entre otras.
Por su parte, en la investigación realizada por Jiménez14 se mencionan tres factores que inciden en el rendimiento académico: el sexo del estudiante, el acceso a becas y el nivel de uso de tecnologías de la información y la comunicación. Es así que diversos estudios señalan distintos factores que repercuten en el desempeño académico, a lo cual cabe mencionar, tal como lo hace Mora18, que existe una gran cantidad de factores a los cuales no se suele tener completo acceso, tales como el entorno familiar, laboral o de salud, pero que, a pesar de ello, la consideración de variables principalmente académicas es de utilidad para la toma de decisiones de los gestores universitarios. También se puede mencionar los trabajos sobre deserción universitaria realizados por Barragán2, Calvache3, Montserrat17, Moreira19 y Munizaga20.
En la UNALM, Huertas y Bullón13 desarrollaron un trabajo en el que evaluaron el rendimiento de los ingresantes del año 2000 luego de cinco años, es decir once semestres académicos después de haber ingresado, llegando a la conclusión de que el 11% logró culminar sus estudios y aproximadamente la mitad se encontraba en situación académica normal, además que la modalidad de ingreso no fue un factor diferenciador en el rendimiento académico.
En un estudio más reciente, llevado a cabo por Delgado6, se analizó el rendimiento de los ingresantes de los semestres 2017-I y 2017-II mediante su nota obtenida en el curso de Matemática y la cantidad de créditos aprobados en su primer semestre de estudios universitarios. Luego de su análisis, concluyó que la nota de matemática del examen de admisión de la universidad fue la más importante para la clasificación del desempeño académico.
El objetivo de esta investigación consiste en encontrar las variables que permitan predecir la situación académica de un estudiante universitario (normal o deficiente) luego de que transcurrieron seis semestres desde su ingreso, usando algoritmos de Machine Learning.
MATERIALES Y MÉTODOS
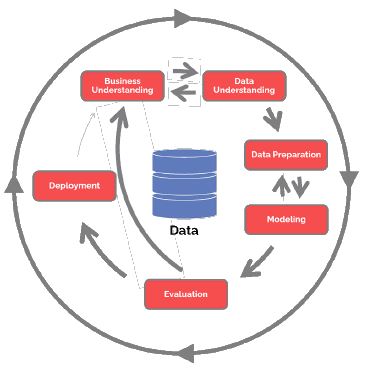
Se utilizó la metodología CRISP (Cross-Industry Standard Process for Data Mining), la cual es una metodología probada para trabajos de minería de datos e incluye seis fases que pueden apreciarse en la Figura 1 y que comprende: entendimiento del negocio, entendimiento de los datos, preparación de los datos, modelación, evaluación y despliegue de resultados. Estas fases son mencionadas por Cichosz4 y Witten, Frank, Hall, Pall25.
Unidad elemental y variables
Un estudiante que ingresó a la UNALM en los semestres 2017-I o 2017-II por cualquier modalidad excepto Graduados y titulados, Traslado externo y CEPRE, y que además cursó por lo menos un semestre de estudios. El conjunto de datos está compuesto por 622 unidades elementales.
La variable objetivo considerada para el modelo es la situación académica del estudiante 6 semestres después de haber iniciado sus estudios universitarios, la cual es una variable dicotómica que toma el valor 0 si la situación académica del estudiante es Normal u Observado, o 1 para todas las demás situaciones académicas. Las variables predictoras pueden ser agrupadas en tres categorías: sociodemográficas, relacionadas al examen de admisión y referidas al primer semestre de estudios.
Metodología Estadística
Se realizó un análisis descriptivo univariado y bivariado con las variables predictoras y la variable dependiente a predecir (situación académica) y se aplicó el algoritmo BORUTA para la selección de las principales variables predictoras. Este algoritmo duplica el conjunto de datos y mezcla los valores en cada columna. Lantz16 denomina a estos valores como variables de sombra. Luego, entrena un clasificador usando el algoritmo Random Forest en el conjunto de datos y calcula el Mean Decrease Accuracy o el Mean Decrease Impurity para cada una de las variables del conjunto de datos. Cuanto mayor sea el puntaje, mejor o más importante es la variable.
El conjunto de datos fue dividido asignando de manera aleatoria el 80% del total de registros para los datos de entrenamiento, y el 20% restante para los datos de evaluación, verificando que en ambas particiones la proporción de estudiantes por situación académica sea similar. Las variables numéricas fueron estandarizadas. Al tener un 84,41% de alumnos en situación académica normal y un 15,59% en situación académica No Normal, se realizó un balanceo de datos utilizando el algoritmo SMOTE, el cual está basado en el principio de oversampling que genera datos artificiales o sintéticos basados en las similitudes del conjunto de variables de la clase minoritaria usando el algoritmo de los vecinos más cercanos o k-nn. Estos algoritmos son descritos por Fernández, García, Galar, Prati, Krawczyk, Herrera8 y Haibo y Yunqian11.
Para la etapa de modelamiento se usó la validación cruzada 10-folds para la estimación y selección de hiperparámetros de los modelos. Se usaron los siguientes algoritmos, descritos por Gareth9 y Hastie12:
-Regresión logística
-K-NN
-Naive Bayes
-Árbol C5.0
-Árbol CART
-Bagging
-Random Forest
-Gradient Boosting Machine (GBM)
-XGBoosting
-Red Neuronal Perceptrón Multicapa
-Máquina de Soporte Vectorial con kernel lineal (SVL)
-Máquina de Soporte Vectorial con kernel radial (SVM)
Posteriormente, con los tres algoritmos que proporcionaron los mejores indicadores en el entrenamiento y que no estén correlacionados, se realizó un algoritmo de ensamble basado en el promedio de las probabilidades obtenidas y se mejoraron los indicadores usando el punto de corte óptimo sugerido por la curva ROC. Los métodos de ensamble son técnicas para combinar varios algoritmos de aprendizaje con la finalidad de poder construir un algoritmo de aprendizaje más fuerte. Existen ensambles basados en pro- medio, promedio ponderado y voto mayoritario, descritos por Alfaro1, Dixit7, Kumar15, Narayanachar21, Rokach23 y Zhou26. Al mantener la muestra de evaluación sin balancear se usaron indicadores robustos a esta desproporción, tales como la sensibilidad, la especificidad y el accuracy balanceado.
RESULTADOS
Selección de variables predictoras
Como resultado de la comprensión de los datos y aplicando el algoritmo BORUTA se selecciona-ron las siguientes variables predictoras numéricas de la situación académica de un alumno:
PUNTAJE.MATEMÁTICAS: Puntaje obtenido en el área de Matemática en el examen de admisión
PUNTAJE.RM: Puntaje obtenido en el área de Razonamiento matemático en el examen de admisión.
PUNTAJE.FÍSICA: Puntaje obtenido en el área de Física en el examen de admisión
PUNTAJE.FINAL: Puntaje obtenido en el examen de admisión
LENGUA: Nota en el curso de Lengua
QUIM: Nota en el curso de Química
MATE: Nota en el curso de Matemáticas
CREDAP: Número de créditos aprobados en el primer semestre de estudios.
PROMSEM: Promedio ponderado del primer semestre de estudios.
Análisis descriptivo de las variables predictoras
En el primer semestre de estudios, la nota promedio de Matemática fue de 11.1 puntos, para Química su media fue de 10.5, mientras que la nota media de Lengua fue igual a 13.3.
Los estudiantes obtuvieron un primer promedio semestral con media de 12.2 puntos y aprobaron 14.7 créditos en promedio.
El 23.1% de los estudiantes que obtuvieron hasta 13.4 de nota en el área de Matemáticas (mediana de la variable) en el examen de admisión presentaron una situación académica de riesgo, mientras que en el grupo restante (más de 13.4 de nota) esta cifra se redujo a casi la mitad (12.9%).
El 23.8% de los estudiantes que obtuvieron 11 o menos nota en Matemática (mediana de la variable) en el primer semestre presentaron una situación académica de riesgo, mientras que en el grupo restante (más de 11) este indicador alcanzó solo el 6.7%.
El 24% de los estudiantes que aprobaron hasta 15 créditos (mediana de la variable) en el primer semestre presentaron una situación académica de riesgo, mientras que en el grupo restante (16 a más créditos aprobados) este indicador alcanzó solo el 7.1%.
El promedio semestral del primer semestre presentó una alta correlación (mayor a 0.8) con al menos una de las demás variables predictoras, por lo que fue retirado del análisis.
Evaluación de los modelos
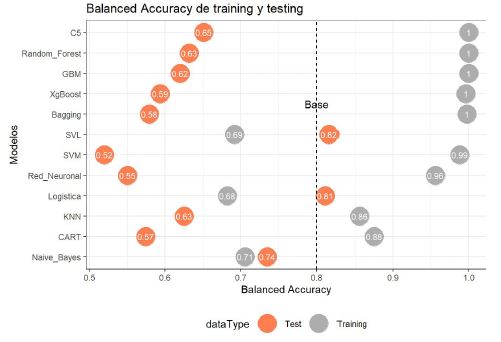
En la Figura 2 se puede observar que los algoritmos que son más estables son la Regresión Logística, Naive Bayes y un SVM con kernel lineal, puesto que con estos se obtuvieron las menores diferencias entre el Balanced Accuracy en los datos de entrenamiento y evaluación, asimismo, alcanzaron el mayor valor en este indicador al utilizar los datos de evaluación. Estos tres algoritmos fueron ensamblados.
Ensamble de modelos
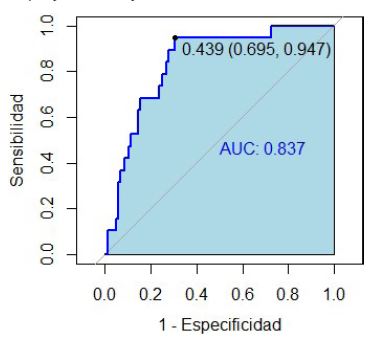
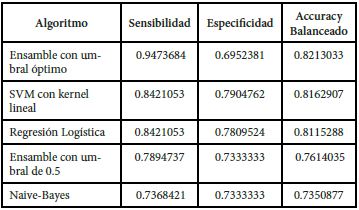
Los resultados de la sensibilidad, especificidad y accuracy balanceado para cada uno de los tres modelos elegidos se muestran en la Tabla 1, así también para el ensamble de éstos, usando el punto de corte tradicional (0.5) y el óptimo sugerido por la curva ROC que se aprecia en la Figura 3. Con este valor óptimo (0.439), la probabilidad de detectar correctamente a los alumnos en situación académica normal es de 0.695, mientras que la detección de estudiantes cuya situación es no normal se realiza con una probabilidad de 0.947.
Tabla 1 Comparación de indicadores para los tres algoritmos y el ensamble con y sin punto de corte óptimo.
DISCUSIÓN
En los hallazgos reportados de esta investigación, las variables sociodemográficas como el sexo, la edad de ingreso y el tipo de colegio de procedencia del estudiante no contribuyeron en la predicción de la situación académica, a diferencia de lo señalado en las investigaciones de Gómez-Sánchez, Martínez-López, Oviedo-Marín10 y Cortez, Tutiven, Villavicencio5. Por otro lado, el estudio de Tapasco, Ruiz y García24 indica que el puntaje conseguido en el examen de admisión no fue una variable significativa en el promedio del estudiante de carreras de ingeniería y ciencias agropecuarias, lo cual concuerda con lo detectado a través de los algoritmos de Machine Learning para alumnos de la UNALM, puesto que solo la nota de Razonamiento Matemático estuvo entre las predictoras más significativas y solo en uno de los algoritmos. Esto se debería a que el examen de admisión mide los conocimientos de los postulantes mas no su aptitud hacia la carrera, un factor importante en su desarrollo académico. Finalmente, las notas de Matemática y Química en el primer semestre siempre aparecen en el grupo de mejores predictoras en los tres modelos ensamblados. Es importante mencionar también que el trabajo de Ocaña22 señala al rendimiento académico previo como una variable que repercute a futuro. Así, los hallazgos reportados por el modelo en estudio podrán ser de utilidad para los tutores, quienes están a cargo del seguimiento de estudiantes universitarios en cuanto a su desempeño académico.
CONCLUSIONES
El modelo de regresión logística, y los algoritmos Naive Bayes y Máquinas de Soporte Vectorial con kernel lineal fueron elegidos por tener un Balanced Accuracy altos y estabilidad de resultados en las muestras de entrenamiento y evaluación.
En los modelos elegidos para el ensamble, las variables relacionadas al primer semestre presentaron mayor importancia que las del examen de admisión. La nota obtenida en el curso de Matemáticas fue una de las más importantes para predecir la situación académica.
Las variables sociodemográficas no fueron relevantes en la predicción del rendimiento académico luego de seis semestres de estudios.
El modelo encontrado debe actualizarse rutinariamente dado que los contenidos y/o formas de enseñanza - aprendizaje van variando a lo largo del tiempo.