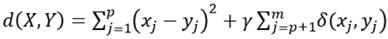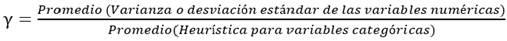I. INTRODUCCIÓN
La preocupación de la comunidad educativa y los responsables de las políticas educativas en las instituciones de educación superiores gira en torno a mejorar la eficiencia académica y del entorno educativo, buscando prevenir problemas como la deserción universitaria que en el Perú anualmente puede alcanzar el 30% de la cantidad de alumnos ingresantes 7, universitarios que por distintas razones como: problemas económicos, falta de vocación en la carrera profesional, falta de apoyo por parte de la universidad y plana universitaria (profesores/orientadores), expectativas defraudadas en la formación y bajo rendimiento académico dejan sus estudios superiores; para ello, es de suma importancia conocer al estudiante que se gestiona desde su inicio en la vida universitaria; conocer sus fortalezas y debilidades, ello permitirá al docente evaluar y proponer las mejores prácticas y metodologías que requieran sus estudiantes.
El objetivo principal de la investigación es lograr identificar cuáles son los distintos grupos de estudiantes que ingresan a una universidad. Se busca adicionalmente caracterizar cada uno de estos grupos y entender sus peculiaridades, conocimientos que promueven la sinergia de esfuerzos entre estudiante - docente, para que este último tenga información del tipo de ingresante que gestiona y con ello diseñe estrategias y renueve sus espacios de enseñanza de manera personalizada, aprovechando toda información del ámbito de la enseñanza 8.
II. MATERIALES Y MÉTODOS
La investigación fue realizada con los datos de los alumnos ingresantes de la Universidad Nacional Agraria La Molina (UNALM) en Lima, Perú durante los semestres 2015-I y 2015-II, los datos fueron obtenidos a partir de la vinculación entre las bases de datos de la Oficina de Estudios y Registros Académicos, del Centro de Admisión y Promoción y la Oficina de Bienestar Universitario y Asuntos Estudiantiles.
La población investigada fueron todos los alumnos ingresantes de la UNALM de las modalidades: Concurso Ordinario y Dos Primeros Puestos de Colegios de Educación Secundaria, con un total de 690 estudiantes. Las variables identificadas en la aplicación de ambas técnicas se muestran en la Tabla 1.
El tipo de investigación fue de carácter descriptivo, se identificó los grupos de ingresantes de la UNALM a través de la descripción de sus variables. El diseño de la investigación fue de carácter no experimental-transversal, ya que se contó con datos de los estudiantes que se recolectaron de diferentes fuentes. Para identificar los grupos se utilizó un algoritmo clustering que es un método exploratorio multivariado iterativo no supervisado 22,23,26 que describe el comportamiento de los objetos en grupos en la fase exploratoria de su investigación, ya que el resultado es exclusivo de los objetos incluidos en el análisis 27 de modo que el analista no asigna las clases previamente, es utilizado en varias áreas desde la década de 1960 10,24. El clustering clasifica los objetos, asignándolos en grupos internamente homogéneos, pero también heterogéneos entre ellos 4,9,17. Uno de los algoritmos clustering más utilizados y conocidos es el K-means 6,15, técnica que distribuye los objetos a través del sistema de particiones en un número k de clústeres previamente definido por el investigador 19,13, sin embargo, este enfoque, tiene un inconveniente frente a la presencia de elementos con outliers 2,12,18 que pueden tener un efecto extremo en el análisis y provocar un agrupamiento inadecuado 3,14,20.
Frente a ello, se han desarrollado algoritmos más apropiados para lidiar con los valores atípicos 21. Un algoritmo más robusto a los outliers y al ruido, que ocurren en un ambiente real sin control es el algoritmo K-medoid 5, el cual se basa en similitud 1. En lugar de utilizar la media convencional, se utiliza medoids para representar los clústeres 16.
El medoid es un elemento del conjunto de datos y es el más centralizado del conjunto de datos. El algoritmo K-medoids inicia con la selección aleatoria de k elementos de datos como centros iniciales para representar los k clústeres, los elementos restantes se incluyen en el grupo que tiene el medoid más cercano a ellos y posteriormente se determina un nuevo centro que puede representar mejor al grupo. En cada iteración, todos los elementos distintos a los centros se asignan nuevamente a los clústeres que tienen el medoid más cercano, provocando que los medoids alteren su ubicación.
El algoritmo minimiza la suma de las distancias entre cada elemento de datos y su correspondiente medoid, este ciclo se repite hasta que ningún medoid cambie su colocación, esto marca el final del proceso y se tienen los clúster finales. La ubicación de cada centro puede cambiar en cada una de las  iteraciones, así se encuentran los k clústers que representan n objetos de datos; el algoritmo fue diseñado para no depender del orden de las observaciones o una semilla inicial, debido a que prueba todas las posibles combinaciones, por lo que siempre converge en la misma solución.
iteraciones, así se encuentran los k clústers que representan n objetos de datos; el algoritmo fue diseñado para no depender del orden de las observaciones o una semilla inicial, debido a que prueba todas las posibles combinaciones, por lo que siempre converge en la misma solución.
Para evaluar cuán diferente son dos observaciones de tipo mixto X e Y con m atributos, donde se tiene p atributos numéricos y m-p atributos categóricos, el algoritmo calcula la disimilitud 11, como:
donde el primer término es la medida de distancia euclidiana al cuadrado en los atributos numéricos y el segundo es la medida de disimilitud de coincidencia simple en los atributos categóricos, siendo 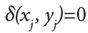 para
para 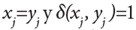 para
para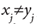 , γ es un peso para atributos categóricos, introducido para evitar favorecer cualquier tipo de atributo. Un cálculo estimado de γ es de la siguiente manera:
, γ es un peso para atributos categóricos, introducido para evitar favorecer cualquier tipo de atributo. Un cálculo estimado de γ es de la siguiente manera:
donde la heurística para variables categóricas se calcula como: 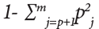 o
o 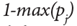 con j = p+1,…,m; siendo pj la proporción de la categoría j en la variable cualitativa. La solución para encontrar el mejor algoritmo clustering y el número óptimo de conglomerados k se llama generalmente validez del clúster. Para esta investigación, se utilizó el Índice de validación de Dunn 25, cuyo objetivo es identificar un conjunto de clústeres que sean compactos, con una varianza pequeña entre los miembros del clúster, y que éstos estén bien separados de los miembros de otros clústeres. Un valor más alto del índice de Dunn indica un mejor rendimiento del algoritmo de clustering, tiene un valor entre cero e infinito.
con j = p+1,…,m; siendo pj la proporción de la categoría j en la variable cualitativa. La solución para encontrar el mejor algoritmo clustering y el número óptimo de conglomerados k se llama generalmente validez del clúster. Para esta investigación, se utilizó el Índice de validación de Dunn 25, cuyo objetivo es identificar un conjunto de clústeres que sean compactos, con una varianza pequeña entre los miembros del clúster, y que éstos estén bien separados de los miembros de otros clústeres. Un valor más alto del índice de Dunn indica un mejor rendimiento del algoritmo de clustering, tiene un valor entre cero e infinito.
III. RESULTADOS
Para aplicar el algoritmo K-medoid es necesario conocer a priori el número de clústeres k a formarse. En este caso, se utilizó el índice de validación interna de Dunn, calculándolo de manera iterativa cambiando el número de clúster y el valor de semilla inicial, el valor de k seleccionado fue aquel que permitió obtener el índice de Dunn más alto.
Se observa en el Tabla 2 que al aplicar el algoritmo K-medoid los valores del índice de validación interna de Dunn óptimos fue 0.16 por lo que el número clúster óptimo es k=3.
Analizando los resultados obtenidos, se realizó la Tabla 3 de resumen general para caracterizar cada uno de los grupos de ingresantes 2015 de la UNALM. Asimismo, se obtuvo que el 36% de los ingresantes pertenecen al clúster 1, el 42% al clúster 2 y el 22% al clúster 3.
Se observó que el clúster con mayor porcentaje de alumnos ingresantes fue el 2 con 42%, dado los resultados obtenidos los ingresantes se clasificaron en:
Con el fin de validar los resultados obtenidos de la segmentación se cruzó esta información con el promedio ponderado acumulado de los alumnos que obtuvieron al término de su primer año de estudios superiores, ya que en este período los universitarios llevan cursos generales que buscan reforzar sus conocimientos adquiridos antes de ingresar a la universidad. Para el análisis se clasificó el promedio ponderado acumulado como:
EXCELENTE: notas ente 16.5 y 20,
BUENO: notas entre 12,5 y 16.5,
REGULAR: notas entre 10,5 y 12.5 o
MALO: notas entre 0 y 10.5
Todo esto permite entender que los clústeres 2 y 3, son los perfiles de ingresantes que deben ser atendidos con prioridad por autoridades pertinentes dentro de la institución, a través de diversas estrategias educativas, apoyo económico y orientación con el fin de que a futuro no tengan bajo rendimiento académico, retraso en sus estudios, dilatación del tiempo de estudio, deserción, entre otros.
V. CONCLUSIONES
Al aplicar el algoritmo de clustering K-medoid, es posible agrupar a los ingresantes de una universidad pública respecto a sus variables socioeconómicas, demográficas y de rendimiento educativo, se pudo identificar 3 tipos de ingresantes cada uno con características diferentes, se denominaron:
Ingresante previsto, Ingresante en proceso e Ingresante en inicio; este último dado sus características necesita mayor tiempo de acompañamiento e intervención del consejero de acuerdo con su ritmo y estilo de aprendizaje frente a los otros segmentos, por otro lado el Ingresante previsto puede ser considerado el grupo de ingresantes con mejores características para la universidad.