Introducción
La geometría es una rama fundamental de las matemáticas que estudia las propiedades y relaciones de las figuras en el espacio y en el plano. Para Crompton et al. (2018) la geometría es el estudio de las propiedades, relaciones y transformaciones de objetos espaciales en un sistema definido. Esta es una asignatura que puede ser relacionada con aspectos del entorno en el que vivimos; y cuando a los temas de geometría se le da un contexto, se facilita su comprensión.
La enseñanza de la geometría es una tarea importante en la educación porque desarrolla en el estudiante habilidades para conceptualizar, razonar y argumentar (Gamboa y Ballestero, 2010). Sin embargo, se ha identificado que muchos estudiantes tienen dificultades para comprender los conceptos básicos de la geometría y aplicarlos en situaciones reales (Silmi et al., 2022). Esta dificultad puede deberse a una variedad de factores, como la falta de exposición a la geometría en la vida diaria, la metodología de una enseñanza inadecuada y la carencia de habilidades matemáticas básicas (Giarrizzo, 2021). Por lo tanto, es fundamental explorar las dificultades en la enseñanza de la geometría para mejorar la calidad del aprendizaje y los resultados académicos de los estudiantes.
Para Aray et al. (2019) uno de los problemas en la enseñanza de la geometría es la dificultad que existe para que los estudiantes logren pasar de la descripción de las figuras hacia un proceso más formal, basado en razonamiento y argumentación. Como consecuencia de esto, Campos (2019) ha mencionado que la resolución de ejercicios y problemas de geometría ocasionan dificultades a los jóvenes, y que esto se manifiesta en las pruebas de ingreso a la educación superior.
En Ecuador, el currículo de geometría se ha diseñado para promover el desarrollo de competencias matemáticas en los estudiantes mediante el análisis, la interpretación y la construcción de objetos geométricos. Fraga et al. (2020) mencionan que a través del análisis y construcción, los estudiantes pueden desarrollar habilidades de pensamiento lógico, crítico y analítico, que son fundamentales para su desarrollo cognitivo. Según el Ministerio de Educación de Ecuador (2016), el programa de geometría usa metodologías basadas en la resolución de problemas, modelización, comunicación y argumentación. Allí, se desarrollan diferentes conceptos como puntos, líneas, ángulos, figuras bidimensionales y tridimensionales, transformaciones geométricas y sistemas de coordenadas.
El currículo ecuatoriano prevé una priorización en el desarrollo de los temas, y distingue contenidos imprescindibles y deseables; por esto, Bravo Guerrero (2020) explica que el currículo debe adaptarse a las necesidades específicas del contexto de los estudiantes y del mundo actual. En geometría, los temas y ejercicios deben adaptarse y contextualizarse para que se visualice su aplicabilidad y mejore su comprensión.
El currículo ecuatoriano está fundamentado en el constructivismo. En palabras de Vygotsky (1978) esta es una teoría del aprendizaje que enfatiza en la construcción activa del conocimiento por parte del sujeto. La idea fundamental de esta corriente es que el aprendizaje implica una interacción activa entre el sujeto y el objeto de conocimiento. Así, Bolaño (2020) menciona que los postulados constructivistas forman parte esencial de la transformación educativa para la enseñanza de las matemáticas, donde el protagonista es el alumno, considerando sus intereses, habilidades para aprender y necesidades en el sentido más amplio.
Gardner (2006) propone una teoría amplia del constructivismo, que integra factores biológicos, psicológicos, culturales y sociales en la construcción del conocimiento. Según este autor, cada individuo posee una combinación única de habilidades y aptitudes que influyen en su forma de aprender y construir conocimiento. Partiendo de esta idea, Miranda (2020) explica que un docente constructivista estará permanentemente indagando, convirtiéndose en un investigador que rompe el cerco del determinismo y abre las puertas hacia la búsqueda de nuevos conocimientos, facilitando de esta forma que el estudiante aprenda de forma activa.
Teniendo en cuenta las dificultades que se tienen para la enseñanza de la geometría, al requerir de mucho razonamiento y deducciones lógicas (Bravo Guerrero, 2019), se plantea incorporar un factor relacionado con la asignatura que aporte con motivación para los estudiantes y que despierte interés en la materia. Se ha propuesto desarrollar un contexto histórico alrededor de la geometría como reconstrucción de la evolución del pensamiento, esto facilita comprender el avance de la ciencia conociendo las ideas originales que fundamentan los logros teóricos, su apoyo en las prácticas y aplicaciones, las limitaciones y carencias de ciertos períodos del desarrollo. Esta es una historia de la cual la epistemología y la didáctica se nutren (Corredor y Londoño, 2019).
Para la enseñanza de la geometría, también es importante el uso de materiales manipulables como figuras geométricas elaboradas en cartulina o madera. Hincapié y Riaño (2008) indican que esta actividad favorece la percepción del estudiante, lo cual influye directamente en el desarrollo de su pensamiento geométrico. Debido al vínculo entre el objeto concreto y el concepto, sus dibujos, basados en la percepción, pueden adquirir con mayor facilidad la naturaleza de representación del concepto (Prieto et al., 2022).
Otra posibilidad es la de realizar un recorrido por diferentes lugares fuera del aula. La visita a patios, jardines y edificaciones dentro del campus posibilita a los estudiantes identificar las formas geométricas que se han usado en las construcciones, mobiliario y diferentes elementos que conforman el paisaje. Esto da la posibilidad de que esas figuras planas y sólidos tratados de forma teórica en las aulas, puedan encontrarse como aplicaciones en la vida real (Bravo Guerrero, 2019).
Bajo la perspectiva constructivista, el uso de la tecnología pasa a ser un componente importante para desarrollar los temas del bloque de geometría, como las figuras planas y espaciales. El Ministerio de Educación de Ecuador (2016) promueve el uso de herramientas como software de geometría dinámica, la calculadora gráfica y el internet para la resolución de problemas y la visualización de figuras geométricas. Riofrío et al. (2019) mencionan que el uso de tecnología en la clase de matemáticas contribuye a una mejor comprensión de los conceptos por parte de los estudiantes. Por otra parte, los estudiantes aprecian que en sus clases se considere el uso de software y dispositivos tecnológicos como recursos para el aprendizaje (Bravo Guerrero et al., 2022).
Metodología
Esta investigación fue un estudio de caso y el diseño metodológico correspondió al enfoque cualitativo. En primera instancia, fueron diseñadas clases de geometría bajo la perspectiva del constructivismo, que luego fueron aplicadas a un grupo de estudiantes de una carrera universitaria. Posteriormente, se aplicó la técnica de Grupos Focales para recopilar información acerca de la intervención realizada.
Se escogieron cuatro temas que corresponden al plan curricular de la asignatura para desarrollar cada uno de esos temas en una clase. Cada clase fue planeada mediante una secuencia de actividades que se organizaron en tres momentos: anticipación, construcción y consolidación de aprendizajes. Estas clases están diseñadas bajo la perspectiva constructivista, afín al enfoque planteado por el Ministerio de Educación (2016) para la educación básica y de bachillerato. Estas clases contienen una serie de actividades que fomentan la participación activa del estudiante en la construcción del conocimiento, el uso de material concreto, recursos tecnológicos y el desarrollo de ejercicios y problemas contextualizados para que se visibilice la aplicación práctica de los contenidos desarrollados.
La intervención se realizó a un grupo de 40 estudiantes que tomaron la asignatura de Geometría en la carrera de Pedagogía de las Matemáticas y Física de la Universidad de Cuenca. Fueron desarrolladas cuatro clases donde se aplicaron las actividades. Los estudiantes fueron divididos en grupos para facilitar la interacción entre ellos y pudieron participar activamente del desarrollo de las clases y manipular los materiales preparados; también usaron software que facilitó la comprensión de los temas.
Una vez desarrolladas las clases donde se aplicaron actividades diseñadas, fue seleccionada una muestra de ocho estudiantes para participar en un grupo focal. Esta técnica consiste en una entrevista grupal aplicada a los investigados y que resulta útil para entender el fenómeno estudiado (Corbetta, 2007). La selección de la muestra se realizó de forma no aleatoria bajo el criterio de cuotas que consiste en escoger la diversidad de los participantes según una cierta característica. En este caso, se escogió como criterio el rendimiento académico: dos estudiantes de altas calificaciones, dos de mediano rendimiento, dos de bajas notas y dos representantes estudiantiles. Esta selección de los participantes correspondió a la búsqueda de todas las opiniones que puedan aportar sobre la temática conversada.
Los estudiantes aceptaron participar del grupo focal luego de que conocieron el documento del consentimiento informado. El documento indicaba que la información que proporcionarían sería tratada de manera confidencial y los reportes serían anónimos. El grupo focal se realizó con la presencia de los ocho estudiantes y el investigador que actúo como moderador. Para llevar adelante la sesión, se preparó un cuestionario guía de preguntas cualitativas que orientó el desarrollo de los temas a tratar (Hernández et al., 2010). La entrevista grupal fue de tipo semiestructurada dado que el moderador podía introducir preguntas para profundizar en temas de interés. La sesión tuvo una duración de una hora y fue grabada para facilitar el posterior procesamiento de la información.
El registro de las participaciones fue transcrito para posteriormente efectuar el análisis de contenido. Se realizaron varias lecturas al documento y luego, mediante un proceso de reflexión, se ordenaron las ideas y temas tratados en la entrevista grupal. De esta manera, se pudo organizar el reporte de la información y la redacción de los resultados.
Resultados
3.1 Diseño de cuatro clases constructivistas
Se diseñaron clases de geometría basadas en el paradigma constructivista. Bajo este enfoque, se aplicaron metodologías activas y de trabajo colaborativo. La planificación buscó que los estudiantes realicen sus trabajos y tareas de forma autónoma. Además, se les incentivó a investigar, a realizar actividades prácticas y del contexto. Los estudiantes realizaron experimentos, manipularon objetos y usaron software que les facilitó el aprendizaje de los temas. El propósito fue que los estudiantes se sientan motivados y dispuestos a aprender, logren un alto nivel de comprensión de los temas y encuentren aplicables a los temas que estudian, es decir, que logren aprendizajes duraderos y de calidad.
La primera clase desarrolló el tema de los grandes personajes de la historia de la geometría: Tales de Mileto, Arquímedes, Pitágoras, Euclides, Descartes, Galileo y da Vinci. Se planificó una serie de lecturas de artículos y publicaciones académicas seleccionadas para que los grupos de estudiantes escogieran un personaje de su preferencia, prepararan una biografía con las principales propuestas en el campo de la geometría de estos personajes y presentasen la información en diapositivas con texto, mapas e imágenes referidas al tema. Conocer el contexto histórico de esos avances e inventos motivó a los estudiantes a aprender geometría. Además, la elaboración de diapositivas les permitió presentar de forma visual los temas. Finalmente, realizaron la presentación a sus compañeros.
En la segunda clase, se manipularon sólidos y se realizó un trabajo práctico. En este, los estudiantes realizaron mediciones de algunas dimensiones de figuras planas como triángulos, cuadriláteros y polígonos; también de sólidos como prismas y pirámides, para posteriormente realizar cálculos de área y volumen de las figuras planas y sólidos. Los alumnos fueron registrando las características de las figuras asignadas y realizaron los cálculos en una ficha previamente elaborada. Esta práctica la realizaron de forma grupal.
Los estudiantes suelen tener dificultades en las destrezas de comprensión espacial, dado que se les complica imaginar las formas que tienen las figuras. Por esta razón, la manipulación de figuras en tres dimensiones les facilitó la comprensión de las mismas, ante cualquier dificultad, conversan entre ellos, se explican e intercambian ideas y el docente brinda apoyo ante cualquier consulta.
Para la tercera clase, durante la primera parte se trabajó en el aula. Allí, los estudiantes pudieron manipular y observar las características de algunas pirámides que fueron repartidas entre ellos. Posterior a eso, se les incentivó a salir en grupos a recorrer el campus de la universidad para identificar dónde se podían encontrar aplicaciones relacionadas con las pirámides. Ellos tenían que fotografiar esas figuras para posteriormente presentarlas a sus compañeros. Cabe resaltar que es de suma importancia que los estudiantes vinculen los temas de geometría con aplicaciones que pueden encontrar a su alrededor pues esto facilita el logro de aprendizajes significativos.
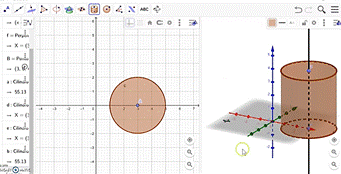
En la cuarta clase, se planteó el uso de software educativo para facilitar la comprensión de sólidos de caras curvas. Se preparó una clase donde se usó software Geogebra y SketchUp, ambas aplicaciones de libre acceso que facilitan el dibujo de figuras en dos y tres dimensiones. Con esto, se trabajó la manipulación de forma virtual, fomentando la participación y el aprendizaje activo.
El diseño de la sesión se realizó mediante la planificación de actividades interactivas, donde se proporcionaron instrucciones, se facilitó la colaboración y se proporcionó retroalimentación; todo esto a medida que los estudiantes trabajaban con los programas educativos. De esta manera, se elaboraron simulaciones de cilindros, conos y esferas, que luego fueron manipulados virtualmente por los estudiantes para ayudarles a caracterizar las figuras. Además, se preparó una hoja de trabajo, donde pudieron apuntar sus características, registrar sus dimensiones y realizar cálculos.
3.2 Resultados del grupo focal
Al consultar a los estudiantes sobre la importancia que ha tenido la geometría en su formación, indicaron que, a pesar de la trascendencia de la asignatura, en el colegio ha existido un escaso abordaje de la materia. Los entrevistados señalaron que durante el colegio se han desarrollado muy pocos temas de estudio: los triángulos como base para la trigonometría, fórmulas de áreas y perímetros de figuras planas y fórmulas del volumen de sólidos. Explicaron que solo lograban un aprendizaje de memoria a través de fórmulas y solo resolvían ejercicios básicos de aplicación directa.
Por otro lado, los participantes reconocieron que actualmente en su formación como docentes de matemáticas, la geometría les ha ayudado a tener una mejor comprensión de ciertos contenidos de otras asignaturas. Mencionaron que la geometría debe ser tratada con una mayor profundidad. Sobre esto, Pedro, uno de los participantes indicó que: “En la materia, se debe saber cómo y de dónde salió eso […] dónde podemos aplicarlo en el entorno […] de esa forma es mucho más fácil entender las fórmulas, de dónde salen, no solo es de memorizar, sino de obtenerlas”.
Explicaron que la geometría no es solo teoría y fórmulas como lo habían visto en el colegio; más bien resaltaron que es importante que se visualice la aplicación que pueden tener los temas en diferentes situaciones de su vida cotidiana. Los estudiantes mencionaron que esto les permite lograr una mejor comprensión de los temas y alcanzar aprendizajes con significado. Ana comentó que: “La geometría es práctica, es aplicada a la vida cotidiana, está a nuestro alrededor”.
Los participantes también mencionaron que la materia es compleja y tiene un nivel elevado de dificultad, pero que en buena medida depende del docente, de su dominio de los temas, de la calidad de las explicaciones que usan para exponer los temas. María lo explicó así: “Hace tiempo tuve un profesor que me complicó con la matemática, yo lloraba porque no le entendía […] después tuve un profesor que sí sabía explicar, sí sabía del tema, y para mí se me hacía súper sencillo todo”.
Ellos indicaron que el docente debe aplicar diferentes metodologías y usar recursos didácticos para desarrollar sus clases, conocer de pedagogía y psicología, tiene que saber cómo manejar sus grupos de estudiantes y saber cómo comunicarse con ellos. Referente a esto, Rosa resaltó: “Somos mundos diferentes, entendemos de maneras diferentes, entonces el profesor tiene que estar capacitado en todo aspecto posible, no sólo en el área técnica o de los números […] más que todo debe poner en práctica la empatía”.
Una vez que se realizaron las cuatro clases donde se aplicaron actividades basadas en el constructivismo, se conversó con los estudiantes buscando sus reacciones a esta nueva forma de desarrollarlas.
Acerca de la clase donde se trabajó en grupos para conocer a los grandes filósofos y pensadores, los estudiantes destacaron la importancia de conocer el contexto histórico, sus reflexiones, postulados y los inventos que crearon. Pedro comentó: “Se ve donde de donde se originó […] se ve esos autores que nunca vas a pensar que tuvieron que ver con la matemática, sólo se dicen que son pensadores, nada más de filosofía, pero te enteras lo que hicieron en la geometría”.
Sobre esta clase, los estudiantes reflexionaron acerca de la utilidad de conocer la historia, el contexto de los temas, los aportes a la geometría, la conexión que esta puede tener con otras asignaturas y la importancia de sus aplicaciones a la vida cotidiana.
Acerca de la clase donde ellos usaron y manipularon material concreto en los temas de prismas y pirámides, indicaron que esto les facilitó identificar y caracterizar las figuras. Además, los estudiantes pudieron calcular la superficie y el volumen de los sólidos a través de ejercicios donde realizaron mediciones. Celina dijo: “Esa actividad que hicimos en grupo, vimos las figuras, los prismas, todo se nos hizo mucho más fácil comprender lo del área y volumen, porque se usó el material didáctico”.
Al reflexionar sobre la aplicación y uso de estos recursos en el futuro cuando ellos sean docentes, explicaron que no todas las instituciones educativas tienen recursos didácticos y tecnológicos. En gran medida, dependerá de la imaginación y creatividad de los profesores para elaborar sus propios materiales de bajo costo e incluso haciendo uso de materiales reciclados para las clases.
Cuando se conversó sobre la visita de observación que realizaron a diferentes ambientes del campus de la universidad, ellos explicaron que pudieron identificar techos, monumentos, toldos, chimeneas, entre otros objetos que tenían esta forma. Rosa afirmó: “En esa salida que hicimos vimos las figuras, las pirámides, sus formas, a mí se me hizo fácil comprenderlas”. En esta observación, los estudiantes entendieron cuán importantes son esas figuras, pues hay muchos objetos donde estas formas se plasman. Esto los motivó a estudiar dichas figuras, profundizar en su comprensión y realizar cálculos.
También se realizó una clase donde se usaron aplicaciones previamente elaboradas de software educativo de uso libre para explicar los sólidos de caras curvas. Este software les permitió a los estudiantes manipular esos sólidos de forma virtual, describir las formas y sus características. Los estudiantes reflexionaron que las instituciones y los jóvenes tienen limitaciones en cuanto a poseer dispositivos tecnológicos donde puedan usar estos programas, Sonia manifestó que “en muchos colegios no hay computadoras, por lo menos en zonas rurales. También, la mayoría de los niños no tiene un celular, por lo tanto, es muy difícil aplicar el software”.
Al realizar una comparación entre sus clases de geometría recibidas en el colegio y en la universidad, bajo el enfoque constructivista, mencionaron que en el colegio priorizan el desarrollo de la secuencia de temas del álgebra y dan poco espacio a los temas de geometría, aunque según el plan curricular oficial la geometría se debe abordar en los diferentes niveles de la educación. José comentó “más dan álgebra en los colegios, más dan algebra que geometría […] un bloque y ahí murió, y entonces solo dan cuadrados, rectángulos”.
Los participantes mencionaron que durante dos años realizaron estudios virtuales debido a la pandemia de Covid-19, lo que perjudicó la calidad sus aprendizajes. Los entrevistados consideraron que no tienen conocimientos sólidos. Ellos reflexionaron que en el futuro van a ser docentes de geometría y deben tener buenos conocimientos de lo disciplinar y lo pedagógico. María mencionó “nosotros tenemos que saber cómo enseñar esos temas […] llevar cosas creativas para que ellos entiendan […] en geometría las figuras son en 3D y ellos de ley no van a entender en el pizarrón algo así, entonces ellos tienen que ver, observar, palpar cómo son las figuras”.
Sobre las cuatro clases diseñadas bajo el constructivismo, indicaron que son nuevas formas de enseñar y aprender, distintas a las tradicionales. Estas clases les dejaron muchas ideas para aplicarlas en el futuro cuando sean docentes. Pedro concluyó “es como una nueva forma de aprender, porque nosotros estamos acostumbrados a aprender de una forma tradicional, que es que es pizarra y marcadores […] es como una forma de aprender más actualizada, didáctica y práctica […] acá hemos aprendido nuevas cosas para formar a otras personas”.
Explicaron que puede ser difícil desarrollar clases constructivistas porque estas toman más tiempo del que se dispone en el colegio, pero muchas de esas ideas podrían ser aplicadas para elevar la calidad de la enseñanza. Los participantes consideraron que las clases mejoraron la comprensión, motivación, investigación, el trabajo colaborativo y la contextualización de los temas.
Conclusiones
El docente tiene un importante rol bajo el paradigma del constructivismo: preparar clases que incentiven el aprendizaje activo por parte de los estudiantes y el logro de aprendizajes duraderos. Además, fomentar el pensamiento crítico y la resolución de problemas al utilizar herramientas para construir y analizar figuras geométricas, así como para realizar cálculos y demostraciones matemáticas.
Las clases desarrolladas tuvieron como objetivo promover un aprendizaje efectivo de la geometría a través de diferentes estrategias. En primer lugar, se enfocó en que los estudiantes conozcan el contexto histórico de esta disciplina, que les facilitase comprender mejor los conceptos y aplicaciones. Además, se fomentó el uso de material didáctico y el uso de recursos tecnológicos para manipular y experimentar con las figuras geométricas, lo cual facilita su comprensión.
Por otro lado, se realizó una actividad de campo donde los estudiantes tuvieron la oportunidad de aplicar lo aprendido en el aula, identificando y caracterizando las figuras geométricas en su entorno. Esto les permitió hacer conexiones entre la geometría y la realidad, fortaleciendo la comprensión de los conceptos.
Finalmente, los estudiantes expresaron que se sintieron motivados al trabajar con metodologías activas y colaborativas, ya que el uso de recursos didácticos y virtuales les ayudó a comprender de manera más sencilla temas que suelen ser complejos. Asimismo, las visitas al campo para observar la aplicación de los conceptos estudiados les dieron sentido y utilidad práctica a los temas estudiados, lo que consideraron que fomenta un aprendizaje significativo y perdurable.