Introducción
El Ecuador se encuentra en la zona con mayor peligrosidad sísmica, localizada en las costas continentales e insulares del Océano Pacífico conocida como el Cinturón de Fuego, lugar en el que ocurren la mayor parte de sismos a nivel mundial (Cueva, 2017).
Nuestro país es un territorio sísmicamente activo, que históricamente ha sido afectado por numerosos terremotos muy destructivos; entre los cuales, se pueden citar los terremotos de: Esmeraldas en 1906 (M=8.8), uno de los más grandes registrados en el mundo, Ambato en 1949 (M=6.8), que dejó cerca de 5050 fallecidos (USGS), Reventador en 1987 (M=6.1 y 6.9), que provocó deslizamientos de lodo, avalanchas de rocas y la destrucción parcial del oleoducto ecuatoriano, Bahía de Caráquez en 1998 (M=7.2), que afectó cerca del 60% de las edificaciones de la zona (Ortiz, 2013), Pedernales en 2016 (M=7.8). Estos sismos demostraron que gran parte de la infraestructura presenta una alta vulnerabilidad sísmica, provocando que las autoridades tomen parte en el asunto e inicien programas que permitan disminuir el riesgo (Cueva, 2017).
La no concordancia entre la estructura proyectada por el ingeniero calculista y la construida, la calidad de los acabados y las excesivas derivas permitidas en el análisis son las causas principales de los daños. En el análisis convencional de estructuras aporticadas, usualmente se asume que solo las vigas, las columnas y la cimentación constituyen el esqueleto de la estructura y, en consecuencia, son los únicos elementos que se consideran al evaluar su resistencia, rigidez y ductilidad. Consecuentes con este planteamiento, los muros divisorios y de fachada, indispensables en cualquier construcción, deberían ser independientes del sistema estructural y no deben afectar su funcionamiento; para ello, deben aislarse de la estructura mediante un adecuado procedimiento constructivo. El aislar los muros de la estructura complica y encarece el procedimiento de construcción; razón por la cual, generalmente esto no se realiza, y la mampostería adosada a las columnas restringe el movimiento relativo entre dos pisos consecutivos alterando el modelo concebido para el análisis (Rochel, 1993).
La mampostería no estructural es un sistema que consiste en la colocación de bloques de hormigón o arcilla unidos con mortero entre sí, con el fin de generar paredes divisorias resistentes y duraderas. Este sistema es el más empleado actualmente debido a que presenta varias ventajas, tanto a nivel económico como constructivo. La principal ventaja es la reducción del peso de los muros en comparación con muros de hormigón armado (Espinosa, 2018).
En el proceso de modelación de una estructura, al tener en cuenta las cargas sobre el muro de mampostería, se debe también valorar la resistencia de la pared para lograr resistir esas cargas. De ahí la necesidad del ingeniero de conocer que puede debilitar o fortalecer la resistencia del muro a diseñar, ya que, dependiendo de su rigidez, así será su resistencia a las cargas que lo someten (Moya, 2011).
La mayor degradación de rigidez se presenta en los ciclos a bajas distorsiones, incluso menores que las asociadas al primer agrietamiento inclinado en la mampostería. Esto significa que, aun cuando el daño no es observable, la estructura pierde rigidez ante sismos de intensidad baja y moderada (Alcocer, 1997).
En investigaciones previas, Barreno (2018) realizó modelaciones de estructuras de hormigón armado sin considerar la presencia de paredes de ladrillo y bloque, y considerando la presencia de éstas. Para determinar su contribución en la resistencia del pórtico, usó modelos matemáticos de diagonales equivalentes, basados en teorías de elementos finitos.
Centeno (2019) planteó la reducción de las excentricidades generadas por la presencia de paredes mediante una combinación de diferentes tipos de materiales y su redistribución. Para esto, consideró paredes de ladrillo y bloque. La combinación de paredes con diferentes propiedades físicas y mecánicas y su redistribución permitió reducir de manera significativa las excentricidades producidas al usar un solo tipo de mampostería.
Muchas veces la falta de consideración de mampostería en las modelaciones se da por la falta de conocimiento del aporte de la rigidez de estas membranas al sistema y esto conlleva a modelos matemáticos que no se ajustan al comportamiento real de las estructuras, generando resultados erróneos. Hasta la fecha de realización del estudio, no se encontraron en bibliografía aportes que contribuyan a relacionar los factores de rigidez de mampostería en la modelación de membranas en edificios. El objetivo de esta investigación es determinar factores de rigidez de membrana, usados para modelar, en edificaciones de hormigón armado, mampostería de ladrillo y bloque, mediante elementos finitos. Para esto, se han considerado diagonales equivalentes y elementos tipo “Shell” en función de la variación de aberturas y luces del edificio. Los tipos de elementos “Shell” están provistos en numerosas herramientas computacionales para el análisis y diseño estructural. Con este estudio se pretende aportar una herramienta que permita obtener de manera rápida los factores de rigidez de membrana, de acuerdo con la configuración estructural lo que ayudará a modelar de forma ágil la mampostería confinada en edificaciones de hormigón armado, considerándola como un elemento tipo “Shell”.
Metodología
Descripción de los materiales
Las propiedades de los materiales considerados como mampostería se obtuvieron de diferentes investigaciones, entre ellas, la investigación realizada por Zamalea (2013) presenta una amplia observación de lo disponible, concretamente en la ciudad de Cuenca (Ecuador), en relación con la mampostería. En esta investigación se utilizó tanto bloque de hormigón y ladrillo cerámico, considerando los siguientes resultados del módulo de elasticidad: E 𝑙𝑎𝑑𝑟𝑖𝑙𝑙𝑜 =2430 MPa y 𝐸 𝑏𝑙𝑜𝑞𝑢𝑒 =1935 MPa. En la investigación de Moreno & Rodas (2017) se obtuvieron los valores de masa por unidad de volumen del ladrillo, 𝜌=17.45 𝑘𝑔/ 𝑚 3 , un peso por unidad de volumen de: 𝛾=16.46 𝑘𝑁/ 𝑚 3 y un módulo de Poisson de: 𝑣=0.25. Para la mampostería de bloque, Páez (2014) determinó una masa por unidad de volumen de: 𝜌=11.40 kg/ 𝑚 3 , un peso por unidad de volumen de: 𝛾=10.76 𝑘𝑁/ 𝑚 3 , y un módulo de Poisson de: 𝑣=0.2.
En base a la norma Ministerio de Desarrollo Urbano y Vivienda (MIDUVI) (2015a), las propiedades del hormigón armado utilizadas fueron: módulo de elasticidad 𝐸𝑐=4.7∗ 𝑓′𝑐 , resistencia a la compresión 𝑓 ′ 𝑐=21𝑀𝑃𝑎, peso por unidad de volumen 𝛾=24.54 𝑘𝑁/ 𝑚 3 , módulo de Poisson 𝑣=0.2, y para el acero se usó un límite de fluencia de 𝑓𝑦=420 𝑀𝑃𝑎.
Cargas
Las cargas de análisis consideradas en las estructuras modeladas en tres dimensiones (3D) fueron: cargas verticales y cargas horizontales. Las cargas verticales consideradas fueron: carga viva y carga muerta (peso propio de las losas, paredes de mampostería, acabados y enlucidos). La carga viva se determinó en función de la ocupación de la edificación. Los valores de las cargas muertas que se asignaron sobre la losa fueron de 5.29 𝑘𝑁/ 𝑚 2 . Los valores de la carga viva fueron de 2 𝑘𝑁/ 𝑚 2 , (MIDUVI, 2015b), valor que se usó en edificaciones de uso residencial y de 0.7 kN/ 𝑚 2 , para la losa inaccesible de cubierta. Las cargas horizontales debidas al sismo se consideraron de acuerdo a las disposiciones del MIDUVI (2015c); los parámetros para la carga lateral fueron: tipo de suelo “D”, factor de reducción de respuesta para estructuras 𝑅=8, aceleración máxima esperada o factor de zona 𝑍=0.4𝑔, factor de importancia 𝐼=1, y los coeficientes de irregularidad en planta Φp=1 e irregularidad en elevación Φe=1. Con estos factores se obtuvo el espectro de diseño y cortante basal. Por otro lado, las combinaciones de carga usadas fueron las establecidas en el (MIDUVI, 2015b). Para el análisis de los pórticos modelados en dos dimensiones (2D) se asumieron cargas sísmicas con los valores que se observan en la (a) (b)
Configuración estructural
En este estudio se consideraron dos configuraciones estructurales, una para el modelo en 2D y otra para el modelo en 3D. En base a los resultados de los modelos en 2D se establecieron los factores de rigidez de membrana f11, f22 y f12; mientras que los modelos en 3D se usaron para la comprobación y aplicación de los factores.
El modelo de 2D consideró pórticos de un vano, con cinco pisos, y el último piso se consideró como una losa inaccesible. Para determinar si existen variaciones en los resultados en función de la tipología estructural, en el modelo en 3D consideraron tres configuraciones diferentes:
Modelo 1 (Comprobación de factores): Una estructura de cinco pisos, conformada solo por un vano en cada sentido, con la misma luz de vano.
Modelo 2 (Aplicación de factores): Una estructura de cinco pisos, conformada por tres vanos en cada sentido, con diferentes luces de vano.
Modelo 3 (Aplicación de factores): Una estructura de seis pisos, conformada por cuatro vanos en cada sentido, con diferentes luces de vano.
Modelación muros de mampostería confinada
La modelación de los muros de mampostería confinada se la realizó usando diagonales equivalentes y elementos tipo “Shell”, tanto para la mampostería de bloque como de ladrillo. Para la modelación de los muros de mampostería confinada se consideraron propiedades físicas y mecánicas de los materiales, tales como: módulo de elasticidad, peso específico, masa por unidad de volumen y módulo de Poisson.
Modelación de la mampostería considerándola como elementos tipo “Shell”
Bajas (2015) manifiesta que los elementos tipo “Shell” son también conocidos como elementos de superficie, es decir, tienen tres grados de libertad, razón por la cual, el elemento “Shell” puede absorber los esfuerzos. Además, las dimensiones son comparables entre sí, o bien dos de sus dimensiones son más grandes que la tercera. Se utiliza principalmente para modelar áreas que pueden ser de losas y muros de mampostería, o cualquier estructura que presente la condición antes planteada.
Para la modelación de las mamposterías de ladrillo y bloque con elementos “Shell”, se ingresaron las propiedades del peso específico y la masa por unidad de volumen, para que se calcule el peso y la masa propia del muro.
Bajas (2015) afirma que para asegurar una conexión adecuada de los nodos entre los elementos tipo “Shell”, se debe discretizar a los elementos grandes en elementos más pequeños, pero que no sean muy pequeños, debido a que, si se disminuye en exceso el tamaño de los elementos finitos, el modelo se vuelve más flexible, más allá del rango aceptable, y además provoca inestabilidad en el programa. Por este motivo, se realizó una discretización cada 50 cm a los muros de la mampostería.
Modelación de la mampostería considerándola como diagonales equivalentes
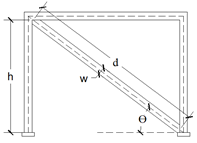
Las diagonales equivalentes, que simulan la presencia de los muros de mampostería confinada, se modelaron como marcos reforzados con diagonales (Braced Frame Model). Las dimensiones de las diagonales equivalentes se calcularon en función de las tablas de factores de reducción de rigidez propuestas por Asteris (2003) para la simulación de muros de mampostería que presentan aberturas a diferentes ubicaciones. Para modelar la diagonal equivalente, se necesita el valor del peso específico y masa por unidad de volumen con valores iguales a cero, ya que el peso y la masa de la diagonal no representa el peso y la masa de una pared. Por lo tanto, se asignó de forma independiente en el modelo el peso y la masa de la pared como cargas distribuidas y masas adicionales sobre las vigas que soportan los muros.
Modelo matemático de la diagonal equivalente
Asteris (2003) presentó resultados analíticos sobre la influencia del tamaño de la abertura y su posición en la pared de mampostería en la respuesta sísmica de los pórticos rellenos de mampostería, según el método de los puntos de contacto. Aquí, la principal condición límite física entre la mampostería de relleno y el pórtico es que el panel de relleno no puede entrar en el pórtico circundante; las únicas condiciones naturales aceptadas entre la mampostería de relleno y el pórtico son el contacto o la separación (puntos de contacto). El problema se estudia en la región elástica y la relación de reducción de rigidez estimada, definida como la rigidez con la abertura de la pared que se utiliza para la comparación con los datos bibliográficos. La acción general entre el marco y el relleno se ve afectada negativamente a medida que la posición de abertura se mueve hacia la diagonal de compresión, es decir la estructura se vuelve más flexible.
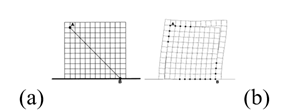
Figura 2: Mallado de mampostería. (a) Diagonal en compresión, (b) Puntos de contactos de mampostería en compresión.
Fuente: Asteris (2003). Lateral Stiffness of Brick Masonry Infilled Plane Frames.
Asteris (2003) desarrolló un modelo matemático para el estudio de los pórticos con diagonales equivalentes que simula la presencia de mampostería, con aberturas en: 1) la esquina superior, 2) esquina inferior, y 3) en el centro de la pared, y variaciones en el tamaño de la abertura de la pared comprendidas entre el 0% y 25%. La Ecuación 2, basada en la propuesta por Mainstone (1971) mostrada en la Ecuación 1, se utilizó en la presente investigación para determinar las dimensiones de la diagonal en compresión.
A partir de una investigación experimental, Stafford (1967) descubrió que la mayor influencia del marco en la rigidez y resistencia del relleno radicaba en la rigidez relativa del relleno-columna, y la influencia de la viga, cualquiera que sea su tamaño, era constante y, por lo tanto, podría ser descartada como una variable. Razón por la cual, en este estudio solo se ha considerado la inercia de las columnas. Asteris et al. (2011) manifiestan que la inercia de las columnas es el valor promedio de las inercias de las columnas adyacentes.
Luego de definir la ubicación y el porcentaje de abertura, se obtuvieron los factores de reducción de rigidez λ a utilizar en la obtención de las dimensiones de la diagonal en compresión, usando las curvas mostradas en la Figura 4. En este trabajo solo se ha considerado la presencia de aberturas en la esquina inferior del muro, de acuerdo con el caso Tipo “A”.
Donde:
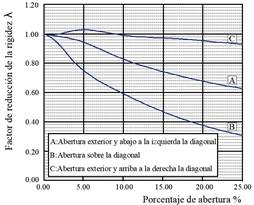
Figura 4: Factor de reducción de la rigidez λ del marco lleno en relación con el porcentaje de abertura para diferentes posiciones.
Fuente: Asteris (2003). Lateral Stiffness of Brick Masonry Infilled Plane Frames.
Modelación estructural
Los sistemas considerados fueron: estructura con pórticos (vigas y columnas), y estructura con pórticos más muros de mampostería (ladrillo y bloque), modelados como diagonales equivalentes y elementos tipos Shell.
Todos los modelos que se realizaron tienen una altura de entrepiso de 3m, con una losa inaccesible en el último piso. Los modelos en 2D y en 3D tuvieron luces comprendidas entre los 3.5 m hasta los 6 m, con variaciones de 50 cm entre cada caso, y adicionalmente, se consideraron en los modelos aberturas en la mampostería confinada que representaron el 0%, 5%, 10%, 15%, 20% y 25% de la pared. Estas aberturas se ubicaron en la esquina inferior de la pared. Para las modelaciones de la mampostería se tuvieron las siguientes consideraciones:
Caso A (Abertura en la esquina inferior), tipo puerta o ventana con una altura estándar de 2.1m, en donde varía el ancho.
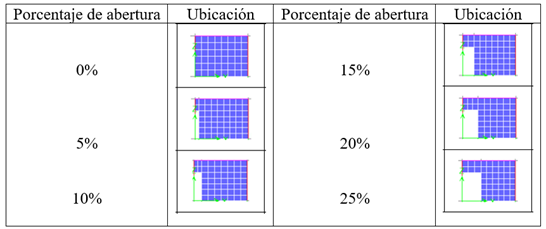
Figura 5: Ubicaciones y porcentajes de abertura en la pared, para el método de elementos tipo “Shell”.
Las modelaciones realizadas en 2D fueron: 256 modelaciones con diagonales equivalentes y 256 modelaciones con elementos tipo Shell. Para el “modelo 1” en 3D, con mampostería de ladrillo y bloque, se realizó el mismo número de modelaciones que en los modelos en 2D.
En los “modelos 2 y 3” en 3D se consideraron estructuras con un mayor número de vanos y pisos; en cada modelo se realizaron combinaciones de muros de ladrillo y bloque y también se combinaron las ubicaciones de las aberturas. Tanto para el modelo 2 y 3 se realizaron seis diferentes modelaciones según el porcentaje de abertura de paredes y una modelación adicional sin paredes. Las estructuras consideradas en este estudio se muestran en las Figura 6, 7, 8, 9, 10, 11.
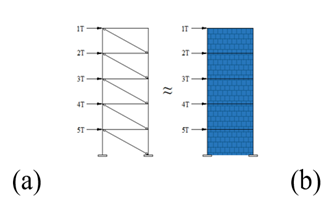
Figura 6: Modelo en 2D y cargas sísmicas aplicadas. a) Sistema con diagonales equivalentes, b) Sistema con elementos tipo “Shell”
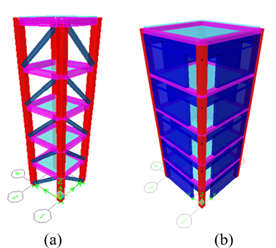
Figura 7: Modelo1 en 3D. a) Sistema con diagonales equivalentes, b) Sistema con elementos tipo “Shell”
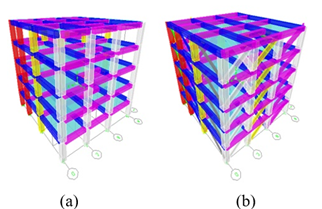
Figura 8: Modelo 2 en 3D. a) Sistema aporticado sin paredes, b) Sistema con diagonales equivalentes.
Figura 10: Modelo 3 en 3D. a) Sistema aporticado sin paredes, b) Sistema con diagonales equivalentes.
En todos los casos, la estructura se conformó de pórticos especiales resistentes a momento, y las vigas y columnas fueron modeladas como elementos tipo “Frame”. Los valores de las inercias agrietadas se obtuvieron de acuerdo al MIDUVI (2015c). Las losas se modelaron como elementos tipo “membrana” con la condición de diafragma rígido.
En las estructuras en 2D y modelo 1 en 3D no se realizaron verificaciones de comportamiento, ya que estos modelos solo se utilizaron para obtener los factores de rigidez de membrana. Luego se realizó la comprobación en los modelos 2 y 3 en 3D (casos generales de aplicación), en los que se realizaron controles de excentricidades de piso, derivas de piso, aplastamiento de columnas, modos de vibración y columna fuerte-viga débil. En la modelación sin la presencia de mampostería se consideró el peso de esta en los controles antes mencionados.
Análisis de resultados
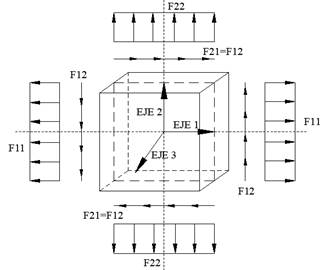
En la modelación con elementos “Shell” se buscó obtener un comportamiento similar a la modelación usando diagonales equivalentes. Para que esto suceda, fue necesario usar factores de rigidez de membrana que simulen la rigidez de la diagonal equivalente. Los factores de rigidez de membrana f11, f22 de los elementos “Shell” modifican el comportamiento a flexión y axial del muro, y dependiendo de la ubicación de los ejes locales, el factor f12 cambia el comportamiento a corte. En la modelación se disminuyó los factores de rigidez de membrana f11, f22 y f12, para que además de considerar solo la rigidez de la diagonal equivalente, también se tome en cuenta: el agrietamiento del muro, la presencia de huecos en la mampostería, discontinuidades y errores de construcción, malas prácticas constructivas y colocación de instalaciones eléctricas y sanitarias.
Los criterios usados para determinar los factores de rigidez de membrana f11, f22 y f12 corresponden a la comparación de los desplazamientos de tope de los modelos en 2D, entre las estructuras modeladas con elementos tipo “Shell” y diagonales equivalentes. Mediante iteraciones se modificaron los factores de rigidez de membrana del modelo con elementos tipo “Shell”, hasta encontrar un resultado de desplazamiento de tope que no tenga diferencias significativas al valor obtenido en el modelo con diagonales equivalentes; para esto se realizó un análisis estadístico de variabilidad ANOVA de un factor, con un nivel de significancia del 95%, de las 256 modelaciones con diagonales equivalentes y de las 256 modelaciones con elementos tipo Shell.
Para validar los resultados obtenidos sobre los factores de rigidez de membrana se usaron los modelos en 3D, con las distintas configuraciones estructurales planteadas, comparando el comportamiento estructural, en términos de desplazamientos, derivas de piso y excentricidades en planta, entre los modelos que consideran la mampostería como elementos tipo “Shell” con los modelos que consideran la mampostería como diagonales equivalentes.
Resultados
Factores de rigidez de membrana
Las estructuras en 2D y modelo 1 en 3D se modelaron usando elementos finitos, lo que permitió encontrar los valores de: desplazamientos de piso, derivas de piso y excentricidades en planta. Con estos parámetros se analizó el comportamiento estructural de las edificaciones. En los modelos 2 y 3 en 3D se realizaron modelaciones para la aplicación práctica de los factores de rigidez de membrana, combinando los materiales, diferentes porcentajes de aberturas ubicadas en las esquinas inferiores, y variando las luces en los pórticos. Al realizar la inclusión de muros de mampostería en los modelos, con el método de diagonales equivalentes y con el método de modelación con elementos tipo “Shell”, se compararon los resultados para realizar ajustes y correcciones en los factores de rigidez de membrana f11, f22 y f12. El método de la diagonal equivalente se lo realizó de acuerdo a la investigación de Asteris (2003), considerando varios porcentajes de abertura de pared, a distintas ubicaciones.
Tabla 1: Comparación de resultados de la modelación de mampostería de ladrillo entre el método de diagonales equivalentes y el método de elemento tipo Shell. Estructura 2D y Estructura 3D modelo 1, caso A.
| . | 2D | 3D | |||||||||||
| Diagonal | Shell | f11, f22, f12 | Diagonal | Shell | |||||||||
| Luz | %A | d (mm) | d (mm) | d (mm) * | D (%) * | e (m) | d (mm) * | D (%) * | e (m) | ||||
| 3.5 m | 0 | 20.90 | 19.90 | 0.1186 | 20.20 | 1.92 | 0.90 | 19.90 | 1.90 | 0.90 | |||
| 5 | 21.70 | 20.80 | 0.1281 | 20.60 | 1.93 | 0.89 | 20.20 | 1.91 | 0.89 | ||||
| 10 | 23.70 | 23.00 | 0.1216 | 21.40 | 1.98 | 0.84 | 21.00 | 1.95 | 0.84 | ||||
| 15 | 25.60 | 25.20 | 0.1192 | 22.10 | 2.01 | 0.81 | 21.80 | 1.99 | 0.80 | ||||
| 20 | 27.20 | 27.00 | 0.1242 | 23.30 | 2.08 | 0.74 | 23.00 | 2.06 | 0.74 | ||||
| 25 | 28.60 | 28.70 | 0.1339 | 23.70 | 2.10 | 0.72 | 23.40 | 2.08 | 0.72 | ||||
| 4.0 m | 0 | 18.40 | 17.50 | 0.1170 | 23.20 | 2.32 | 1.12 | 22.90 | 2.29 | 1.12 | |||
| 5 | 19.10 | 18.30 | 0.1249 | 23.60 | 2.33 | 1.11 | 23.20 | 2.30 | 1.11 | ||||
| 10 | 21.00 | 20.40 | 0.1180 | 24.60 | 2.38 | 1.06 | 24.20 | 2.35 | 1.06 | ||||
| 15 | 22.80 | 22.50 | 0.1162 | 25.50 | 2.43 | 1.02 | 25.10 | 2.40 | 1.02 | ||||
| 20 | 24.30 | 24.30 | 0.1213 | 26.90 | 2.51 | 0.95 | 26.50 | 2.48 | 0.95 | ||||
| 25 | 25.60 | 26.00 | 0.1320 | 27.50 | 2.54 | 0.93 | 27.00 | 2.51 | 0.93 | ||||
| 4.5 m | 0 | 16.60 | 15.80 | 0.1140 | 26.70 | 2.78 | 1.34 | 26.30 | 2.75 | 1.34 | |||
| 5 | 17.30 | 16.70 | 0.1199 | 27.20 | 2.81 | 1.33 | 26.70 | 2.76 | 1.33 | ||||
| 10 | 19.00 | 18.50 | 0.1143 | 28.30 | 2.87 | 1.28 | 27.80 | 2.83 | 1.28 | ||||
| 15 | 20.70 | 20.60 | 0.1124 | 29.30 | 2.92 | 1.24 | 28.90 | 2.89 | 1.24 | ||||
| 20 | 22.20 | 22.30 | 0.1179 | 31.10 | 3.02 | 1.17 | 30.50 | 2.98 | 1.17 | ||||
| 25 | 23.40 | 24.00 | 0.1295 | 31.80 | 3.05 | 1.14 | 31.20 | 3.02 | 1.14 | ||||
| 5.0 m | 0 | 15.20 | 14.40 | 0.1110 | 30.70 | 3.33 | 1.57 | 30.20 | 3.29 | 1.57 | |||
| 5 | 15.90 | 15.30 | 0.1165 | 31.20 | 3.35 | 1.56 | 30.70 | 3.30 | 1.56 | ||||
| 10 | 17.60 | 17.20 | 0.1101 | 32.50 | 3.42 | 1.50 | 32.00 | 3.38 | 1.50 | ||||
| 15 | 19.20 | 19.10 | 0.1087 | 33.80 | 3.49 | 1.46 | 33.30 | 3.45 | 1.46 | ||||
| 20 | 20.60 | 20.80 | 0.1142 | 35.90 | 3.60 | 1.38 | 35.00 | 3.55 | 1.38 | ||||
| 25 | 21.80 | 22.50 | 0.1261 | 36.70 | 3.64 | 1.36 | 35.80 | 3.60 | 1.36 | ||||
| 5.5 m | 0 | 14.20 | 13.50 | 0.1074 | 35.20 | 3.96 | 1.80 | 34.70 | 3.91 | 1.79 | |||
| 5 | 14.80 | 14.30 | 0.1119 | 35.80 | 3.98 | 1.78 | 35.20 | 3.93 | 1.78 | ||||
| 10 | 16.50 | 16.10 | 0.1059 | 37.30 | 4.06 | 1.73 | 36.70 | 4.01 | 1.73 | ||||
| 15 | 18.10 | 18.00 | 0.1049 | 38.70 | 4.13 | 1.68 | 38.10 | 4.09 | 1.68 | ||||
| 20 | 19.40 | 19.70 | 0.1107 | 41.20 | 4.27 | 1.60 | 40.20 | 4.21 | 1.60 | ||||
| 25 | 20.60 | 21.50 | 0.1224 | 42.10 | 4.32 | 1.57 | 41.10 | 4.27 | 1.57 | ||||
| 6.0 m | 0 | 13.40 | 12.70 | 0.1038 | 40.20 | 4.67 | 2.02 | 39.60 | 4.61 | 2.02 | |||
| 5 | 14.00 | 13.50 | 0.1076 | 40.90 | 4.70 | 2.01 | 40.20 | 4.63 | 2.01 | ||||
| 10 | 15.60 | 15.20 | 0.1018 | 42.60 | 4.78 | 1.95 | 41.90 | 4.72 | 1.95 | ||||
| 15 | 17.10 | 17.10 | 0.1010 | 44.20 | 4.86 | 1.90 | 43.50 | 4.81 | 1.90 | ||||
| 20 | 18.40 | 18.90 | 0.1069 | 47.10 | 5.02 | 1.83 | 45.90 | 4.95 | 1.83 | ||||
| 25 | 19.60 | 20.60 | 0.1189 | 48.10 | 5.07 | 1.80 | 47.00 | 5.02 | 1.80 | ||||
Nota: * corresponde al valor obtenido en el centro de masas del diafragma rígido (losa)
Tabla 2: Comparación de resultados de la modelación de mampostería de bloque entre el método de diagonales equivalentes y el método de elemento tipo Shell. Estructura 2D y Estructura 3D modelo 1, caso A.
| 2D | 3D | ||||||||||||
| Diagonal | Shell | f11, f22, f12 | Diagonal | Shell | |||||||||
| Luz | %A | d (mm) | d (mm) | d (mm) * | D (%) * | e (m) | d (mm) * | D (%) * | e (m) | ||||
| 3.5 m | 0 | 22.00 | 20.40 | 0.1151 | 20.30 | 1.90 | 0.89 | 20.00 | 1.88 | 0.89 | |||
| 5 | 22.80 | 21.80 | 0.1217 | 20.60 | 1.92 | 0.88 | 20.40 | 1.90 | 0.87 | ||||
| 10 | 24.90 | 23.70 | 0.1184 | 21.40 | 1.96 | 0.84 | 21.10 | 1.93 | 0.84 | ||||
| 15 | 27.00 | 26.00 | 0.1162 | 22.10 | 2.00 | 0.80 | 21.80 | 1.98 | 0.80 | ||||
| 20 | 28.60 | 27.90 | 0.1210 | 22.60 | 2.03 | 0.77 | 22.40 | 2.01 | 0.77 | ||||
| 25 | 30.10 | 29.80 | 0.1306 | 23.10 | 2.05 | 0.74 | 22.80 | 2.04 | 0.74 | ||||
| 4.0 m | 0 | 19.40 | 18.00 | 0.1135 | 23.20 | 2.32 | 1.12 | 22.90 | 2.29 | 1.12 | |||
| 5 | 20.20 | 18.90 | 0.1213 | 23.70 | 2.32 | 1.10 | 23.30 | 2.28 | 1.10 | ||||
| 10 | 22.20 | 21.10 | 0.1149 | 24.70 | 2.37 | 1.05 | 24.30 | 2.33 | 1.05 | ||||
| 15 | 24.10 | 23.30 | 0.1129 | 25.60 | 2.42 | 1.01 | 25.20 | 2.39 | 1.01 | ||||
| 20 | 25.60 | 25.20 | 0.1181 | 26.20 | 2.45 | 0.97 | 25.90 | 2.43 | 0.97 | ||||
| 25 | 27.00 | 27.00 | 0.1286 | 26.80 | 2.48 | 0.95 | 26.50 | 2.47 | 0.95 | ||||
| 4.5 m | 0 | 17.50 | 16.20 | 0.1110 | 26.80 | 2.76 | 1.34 | 26.40 | 2.72 | 1.34 | |||
| 5 | 18.30 | 17.10 | 0.1173 | 27.30 | 2.79 | 1.33 | 26.80 | 2.74 | 1.33 | ||||
| 10 | 20.20 | 19.20 | 0.1110 | 28.50 | 2.85 | 1.27 | 28.00 | 2.81 | 1.27 | ||||
| 15 | 22.00 | 21.30 | 0.1093 | 29.50 | 2.90 | 1.22 | 29.10 | 2.87 | 1.22 | ||||
| 20 | 23.50 | 23.20 | 0.1146 | 30.30 | 2.95 | 1.19 | 29.90 | 2.92 | 1.19 | ||||
| 25 | 24.80 | 25.00 | 0.1259 | 31.00 | 2.98 | 1.16 | 30.70 | 2.97 | 1.16 | ||||
| 5.0 m | 0 | 16.10 | 14.90 | 0.1080 | 30.90 | 3.30 | 1.57 | 30.40 | 3.26 | 1.57 | |||
| 5 | 16.90 | 15.80 | 0.1129 | 31.40 | 3.33 | 1.55 | 30.90 | 3.28 | 1.55 | ||||
| 10 | 18.70 | 17.80 | 0.1068 | 32.80 | 3.40 | 1.50 | 32.20 | 3.35 | 1.50 | ||||
| 15 | 20.40 | 19.80 | 0.1057 | 34.00 | 3.47 | 1.44 | 33.50 | 3.42 | 1.44 | ||||
| 20 | 21.80 | 21.70 | 0.1110 | 34.90 | 3.52 | 1.41 | 34.50 | 3.48 | 1.41 | ||||
| 25 | 23.10 | 23.50 | 0.1226 | 35.70 | 3.56 | 1.37 | 35.40 | 3.54 | 1.37 | ||||
| 5.5 m | 0 | 15.10 | 13.90 | 0.1044 | 35.40 | 3.93 | 1.80 | 34.80 | 3.87 | 1.80 | |||
| 5 | 15.80 | 14.80 | 0.1086 | 36.10 | 3.96 | 1.78 | 35.40 | 3.89 | 1.78 | ||||
| 10 | 17.50 | 16.70 | 0.1028 | 37.60 | 4.04 | 1.72 | 36.90 | 3.98 | 1.72 | ||||
| 15 | 19.20 | 18.70 | 0.1018 | 39.00 | 4.11 | 1.67 | 38.40 | 4.06 | 1.67 | ||||
| 20 | 20.60 | 20.60 | 0.1075 | 40.10 | 4.17 | 1.62 | 39.60 | 4.13 | 1.62 | ||||
| 25 | 21.80 | 22.40 | 0.1190 | 41.00 | 4.22 | 1.59 | 40.70 | 4.20 | 1.59 | ||||
| 6.0 m | 0 | 14.30 | 13.10 | 0.1008 | 40.50 | 4.63 | 2.03 | 39.80 | 4.56 | 2.03 | |||
| 5 | 14.90 | 13.90 | 0.1044 | 41.30 | 4.67 | 2.01 | 40.50 | 4.59 | 2.01 | ||||
| 10 | 16.60 | 15.80 | 0.0987 | 43.00 | 4.76 | 1.95 | 42.20 | 4.69 | 1.95 | ||||
| 15 | 18.20 | 17.80 | 0.0981 | 44.60 | 4.84 | 1.89 | 43.90 | 4.78 | 1.89 | ||||
| 20 | 19.60 | 19.70 | 0.1038 | 45.80 | 4.91 | 1.85 | 45.20 | 4.87 | 1.85 | ||||
| 25 | 20.80 | 21.50 | 0.1155 | 46.90 | 4.96 | 1.81 | 46.50 | 4.95 | 1.81 | ||||
Nota: * corresponde al valor obtenido en el centro de masas del diafragma rígido (losa)
Curvas para la obtención de coeficientes de rigidez de membrana
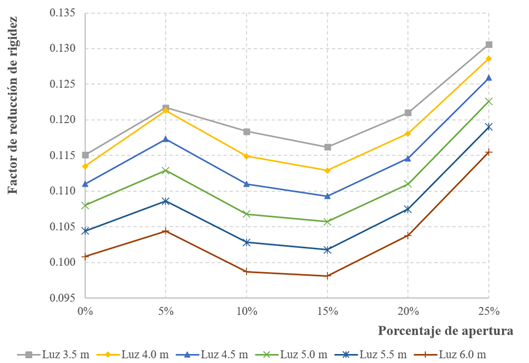
Para obtener de manera rápida los coeficientes de rigidez de membrana, según el porcentaje de abertura y la luz del vano con mampostería confinada, se pueden usar las curvas representadas en las figuras 12 y 13, en las cuales se presenta la variación de los factores de rigidez de membrana, de acuerdo con el caso y el tipo de mampostería.
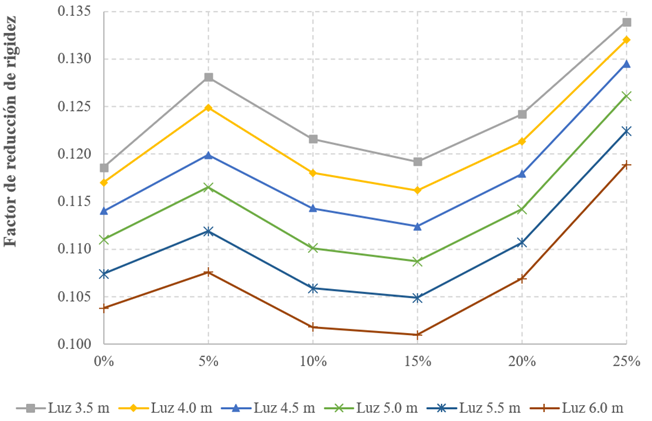
Figura 12: Factores de rigidez de membrana en función del porcentaje de abertura de pared (Ladrillo)
Discusión
La presencia de muros de mampostería confinada en estructuras de hormigón armado produjo cambios significativos en el centro de rigidez independientemente que las paredes presenten o no aberturas hasta un porcentaje del 25% en las edificaciones analizadas, que son el modelo 2 y 3 en 3D; estos resultados coinciden con lo reportado en el estudio de Dias et al. (2022) en donde se concluye que la rigidez, resistencia, ductilidad global y capacidad de disipación de energía de las estructuras mejora durante un sismo gracias a la mampostería confinada. De la misma manera Pallarés et al. (2021) señalan que la mampostería confinada en pórticos de concreto incrementa hasta ocho veces la rigidez en comparación con un pórtico no confinado. Este incremento de rigidez se debe a diagonales que conectan los nodos de la estructura, limitando la deformación relativa de los pisos, que al ser componentes de la estructura principal pasan a formar parte del sistema sismo resistente.
El análisis de la mampostería realizada con elementos tipo “Shell” se basa en el método de los elementos finitos (Bajas, 2015), estos elementos son del mismo espesor de la mampostería. Además, para la modelación con este tipo de elementos se debe tener en cuenta los factores de rigidez de membrana f11, f22 y f12 apropiados. De esta manera, se obtuvieron los resultados del comportamiento estructural de las edificaciones, evidenciando que no existen diferencias significativas al modelar la mampostería con el método de diagonales equivalentes y con el método de elementos tipo “Shell”.
En las Tablas 1 y 2 se muestran los resultados obtenidos del comportamiento estructural, en términos de desplazamientos de tope (d), derivas inelásticas (D) y excentricidades (e), los factores de rigidez de membrana (f11, f22 y f12), de acuerdo con la configuración estructural, el tipo de mampostería y al porcentaje de abertura (%A). Como se puede notar, al usar los factores de rigidez de membrana f11, f22 y f12 apropiados en las estructuras modeladas con elementos tipo “Shell”, los valores de desplazamientos de piso, derivas de piso y excentricidades de piso no presentan diferencias significativas. Los resultados obtenidos en los dos sentidos (X y Y) para las modelaciones en 3D del modelo 1 son iguales, debido a la distribución simétrica de la mampostería en ambos sentidos.
Los factores de rigidez de membrana representados en las Figuras 12, 13, cuando las luces disminuyen (3.5m), se ven afectados por un aumento de rigidez de la diagonal equivalente, lo que ha dado lugar a la obtención de resultados que no son proporcionales a los obtenidos para las luces mayores. Esto puede atribuirse a una mayor extensión de la longitud de puntos de contacto, tal como se presenta en la Figura 2(b), cuando las luces se reducen.
Conclusiones
Después de realizar el análisis de los resultados de derivas, desplazamientos y excentricidades de las estructuras modeladas con muros de mampostería usando diagonales equivalentes y elementos finitos “Shell”, se tienen las siguientes conclusiones:
El centro de rigidez se modificó de manera importante con la incorporación de muros de mampostería confinada, sin importar si las paredes tenían aberturas de hasta un 25% en las edificaciones estudiadas, que corresponden a los modelos 2 y 3 en 3D. También aumentó significativamente la rigidez de la estructura debido a la continuidad de la mampostería desde el primer piso hasta el último piso.
Al usar los factores de rigidez de membrana f11, f22 y f12 para muros de mampostería confinada no existieron diferencias significativas entre los resultados de las modelaciones mediante el método de elementos “Shell” con los obtenidos al usar el método de diagonales equivalentes.
Los factores de rigidez de membrana f11, f22 y f12, se usan para considerar en el modelo el incremento en la rigidez del pórtico debido a la presencia de mampostería. Además, estos factores consideran la disminución de la rigidez de la mampostería debido al uso de materiales prefabricados huecos y poco homogéneos, discontinuidad en la colocación de morteros de pega, errores constructivos, etc. Los factores de rigidez de membrana, por lo antes expuesto, y dependiendo del tipo de mampostería, tipo y porcentaje de abertura y luz del pórtico, presentan reducciones que van desde el 80% al 90%, aproximadamente.
Los factores de rigidez de membrana determinados en este estudio pueden ser usados en modelaciones de estructuras de hormigón armado construidas con mampostería confinada de ladrillo o bloque, con luces comprendidas entre 3.5 m y 6.00 m, aberturas de pared ubicadas en los extremos inferiores, con porcentajes de abertura que pueden variar entre 0% y 25%, alturas de entrepiso comprendidas entre 2.50m y 3.50m, con los valores de módulo de elasticidad de mampostería que imponga el calculista y espesores de pared variable.
Al modelar la mampostería con el método de elementos tipo “Shell”, usando factores de rigidez de membrana apropiados, se simplifica el proceso de modelación, análisis y diseño de una edificación, en relación con el uso del método de diagonales equivalentes.
Contribuciones de los autores
En concordancia con la taxonomía establecida internacionalmente para la asignación de créditos a autores de artículos científicos (https://casrai.org/credit/). Los autores declaran sus contribuciones en la siguiente matriz: