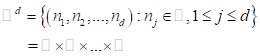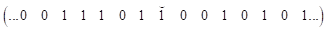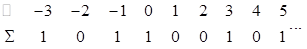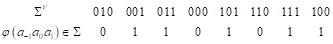Introducción
El vehículo automotor, es un elemento esencial en el estilo de vida de las generaciones modernas. Cada año se fabrican millones de ellos que son distribuidos por todo el mundo y es en las grandes ciudades, donde se presentan mayores problemas FV al momento de ir y retornar del trabajo, utilizando tanto vehículos propios como transporte urbano, además de todo el transporte de carga pesada que debe circular para dotar a las ciudades de insumos para funcionar correctamente. Aunado a esto, al no haber un FV adecuado se presentan problemas de contaminación ambiental, exceso de ruido y personas estresadas, entre otros. Tyagi, Darbha, & Rajagopal (2009), reportaron que en 1994 el índice de congestionamiento de carreteras (en inglés Road Congestión Index, RCI), había crecido 20 % (Schrank, Turner, & Lomax, 1994). También, en lo económico las pérdidas asociadas al congestionamiento del tráfico en Estados Unidos para 2017 fueron aproximadamente de 308 billones de dólares, según Schneider (2018).
La cantidad desbordante de vehículos excediendo la capacidad operacional de las vías, algunos semáforos mal programados y mala distribución de las vías, hacen que ocurra inevitablemente el congestionamiento vehicular. Una solución a esto es hacer nuevas y amplias avenidas, pero esto ocasionaría un costo muy elevado, además las edificaciones grandes y densas no permiten una ampliación como tal. Los modelos matemáticos de FV juegan un papel importante, ya que trabajan sobre las vías existentes a un costo muy bajo, sobre todo, usando el avance electrónico, en telecomunicaciones y computación para inclusive tener una respuesta en tiempo real del FV.
Uno de los modelos matemáticos usados desde los años 90 para modelar el FV es el autómata celular (AC). En el trabajo de Maerivoet y De Moor (2005) se afirma que al ser aplicado al FV “generan modelos computacionales con rendimientos eficientes y rápidos, dichos modelos provienen de la Mecánica Estadística, una disciplina de la Física, con el objetivo de entender el comportamiento del FV macroscópico basado en una descripción mínima de los modelos microscópicos”.
En este trabajo se pretende realizar una revisión de la bibliografía del modelo de AC siguiendo las necesidades que las mismas condiciones del FV han generado. El objetivo de la presente revisión es identificar hacia donde se orientan los temas relacionados con el comportamiento del flujo vehicular. Se espera colocar al investigador o lector interesado en contacto con trabajos publicados, asociados al estudio del FV usando autómatas celulares.
También, se presentan como elementos esenciales de los autómatas celulares el espacio de estados y la regla de interacción entre las células. Esto desde el punto de vista matemático para tener una visión más amplia y profunda del modelo.
Se describen dos modelos, uno determinístico y el otro probabilístico, los que dieron inicio al estudio del tráfico desde los AC; se presentan un par de ejemplos para hacer la lectura más didáctica. La diferencia con respecto a otras revisiones bibliográficas consiste en tomar inicialmente el enfoque de un carril, luego el de dos o múltiples carriles, indicando los problemas tratados recientemente y mostrando los modelos de forma general, mas no la técnica usada para modelarlos computacionalmente, ya que cada autor usa recursos computacionales diferentes.
Metodología
La realización de este artículo se basó en una investigación bibliográfica acerca del FV y los autómatas celulares. Para Reis (2008), la revisión de bibliografía describe un problema que se basa en “[…] las contribuciones secundarias, es decir, en las informaciones de datos extraídos de libros de literatura común y científicos, revistas impresas y virtuales, material audiovisual, entrevistas y documentos, de diferentes autores que tratan el mismo problema seleccionado para el estudio”.
Primero fue realizada una selección de artículos sobre los inicios del estudio del FV en particular de los relacionados con autómatas celulares, como: Greenshields (1934), Chandler, Herman, & Montroll (1958), Gazis, D., Herman, R., & Rothery (1961), Biham, Middleton, & Levine (1992), Wolfram (1983) y Nagel & Schreckenberg (1992).
Se determinó el momento en el que aparecieron los modelos de autómatas celulares para modelar el flujo del tráfico y comprender el modelo de Nagel y Schreckenberg (NaSch), desde el artículo original y su diferencia respecto a los otros modelos de AC para FV de la época. Luego se consideraron modelos publicados en revistas científicas de impacto registradas en Scimago Journal Ranking (2018) como Maerivoet & De Moor, (2005) de Physics Reports, otros en Physical Review A, Physical Review E, Physica A. Estas revistas se encargan de seleccionar artículos con aportes significativos en los temas tratados en cada una de ellas, con la finalidad de comprender el enfoque de los investigadores.
También, fueron considerados el libro de Romero (2012) y los artículos de Wolfram (1983, 1984), para contar con un enfoque pedagógico además del fundamento matemático.
Ingredientes de los autómatas celulares y notaciones básicas
En esta sección se realiza una definición formal matemática de los autómatas celulares determinísticos y se describen los dos modelos que dieron inicio a la teoría de tráfico con AC. Para mejorar la visualización y comprensión de los modelos, se presentan un par de ejemplos.
Autómatas celulares
Según Romero (2012)
Los autómatas celulares fueron introducidos por John von Neumann a comienzos de los años 1950’s. Una vez concluida su participación en la creación del primer computador de propósito general, Von Neumann se propuso desarrollar un robot que tuviese la capacidad de auto-reproducirse. Stanislaw Ulam, colega de von Neumann en el Laboratorio de Los Alamos, le sugirió el uso de la abstracción matemática para lograr su propósito, de forma semejante a la empleada por él en el estudio del crecimiento de cristales; fue así como von Neumann ideó el primer autómata celular… G. A. Hedlund en 1969 escribió un trabajo que es considerado pionero en la formalización matemática de la teoría de los autómatas celulares (Hedlund, 1969).
En esta subsección se siguen las ideas presentadas en Romero (2012). Para definir un AC se necesitan varios elementos los cuales son:
Primero, considere un conjunto de células o de celdas, en matemática retículos. En este caso se consideran un conjunto de células generadas por los números enteros d dimensional (𝑑≥1), esto es (1)
donde ℤ denota el conjunto de los números enteros, 𝑛 1 , 𝑛 2, … 𝑛 𝑑, es una d-úpla ordenada, esto significa que si 𝑛 1 , 𝑛 2, … 𝑛 𝑑, = 𝑚 1 , 𝑚 2, … 𝑚 𝑑, entonces, 𝑛 𝑖 = 𝑚 𝑖 para todo los valores 𝑖∈ 1, 2, …𝑑 . Por ejemplo, el punto 1, 2 es distinto al punto 2, 1 para el caso de ℤ 2 . En el caso 𝑑=1, ℤ 1 =ℤ. A cada elemento de ℤ 𝑑 se le llama célula. En muchos modelos de aplicación se usa un retículo finito o de forma de anillo, esto es, ℤ 𝑁 ={0, 1, … , 𝑁−1} el anillo de los enteros módulo 𝑁, en palabras significa que a la célula en la posición cero se le relaciona con la célula en la posición 𝑁. Es un conjunto importante ya que permite tener operaciones algebraicas en él.
Segundo, el conjunto de estados (en matemática llamado también alfabeto) denotado por Σ. En general este es un conjunto finito que puede ser representado por letras minúsculas o números, por ejemplo Σ= 1, 2, …, 𝑁 o Σ= 0, 1, …, 𝑁−1 . En algunos casos dependiendo del problema a tratar Σ puede ser el anillo de los enteros módulo 𝑁 (Σ= ℤ 𝑁 ). Con estos dos ingredientes, se realiza la configuración de la célula de la siguiente forma: a cada célula de ℤ 𝑑 se le asigna un valor en el conjunto de estado Σ. En Matemática, tal configuración es una función 𝑎: ℤ 𝑑 → Σ.Al conjunto de todas las posibles configuraciones 𝑎: ℤ 𝑑 → Σ (espacio fase del autómata celular) es denotado por Σ ℤ 𝑑 , que dotado de una topología adecuada llamada topología producto se obtiene que Σ ℤ 𝑑 posee todas las propiedades topológicas equivalente al conjunto de Cantor. En el caso particular 𝑑=1 𝑦 Σ= 0, 1 , una configuración 𝑎: ℤ → Σ, se puede denotar de la siguiente forma donde el valor que tiene el símbolo en forma de “v” es la posición “cero” (2)
o de la forma donde en la parte superior se indica la posición de la célula y en la parte inferior en estado que adquirió la célula: (3)
Con esta notación se asume que en la posición y espacio de cada célula tomo el valor del estado, que en el ejemplo es de 0 o 1.
Tercero, el siguiente ingrediente se enfoca con la vecindad, es decir, dependiendo del comportamiento de las células vecinas se actualiza la configuración de un estado de la célula al siguiente. La vecindad es un subconjunto finito 𝑉 de ℤ 𝑑 ,indica la cantidad y en cuales células vecinas se debe observar su comportamiento.
Cuarto, la regla local, se refiere a como actualizar la célula en función de sus vecinos. Los vecinos a observar son los dados por 𝑉. En otras palabras, la regla local que rige los cambios de estados de una célula a la siguiente. Esto matemáticamente es una función 𝜑: Σ 𝑉 → Σ, la cual genera la regla local que regirá al autómata celular. La vecindad más estudiada al principio de los AC, es 𝑉= −1, 0, 1 , que observa al vecino anterior, el estado actual y al vecino siguiente. Recuerde Σ 𝑉 es el conjunto de todas las posibles configuraciones que puede tener las células de 𝑉.
Con estos cuatro ingredientes un autómata celular en una 4-úpla ℤ 𝑑 ,Σ,𝑉,𝜑 donde la transición de una célula a la siguiente viene dada por la aplicación global 𝐹: Σ ℤ 𝑑 → Σ ℤ 𝑑 , que a cada configuración 𝑎: ℤ 𝑑 → Σ y cada célula 𝑛 = 𝑛 1 , 𝑛 2, … 𝑛 𝑑, ∈ ℤ 𝑑 se va a actualizar al siguiente estado de la forma: 𝐹 𝑎 𝑛 =𝜑(𝑎 | 𝑉+ 𝑛 ), donde 𝑎 | 𝑉+ 𝑛 es la restricción de 𝑎 al conjunto finito 𝑉+ 𝑛 = 𝑚+ 𝑛 :𝑚 ∈𝑉 y se puede ver como un elemento de Σ 𝑉 que luego, 𝜑 le asocia un estado en Σ. Para ver la evolución de una configuración inicial 𝑎 es la sucesión 𝑎, 𝐹 𝑎 , 𝐹 2 𝑎 , 𝐹 3 𝑎 , …, 𝐹 𝑘 𝑎 , …, esto es la órbita de 𝑎 respecto a 𝐹, donde 𝐹 𝑘 𝑎 significa que se compone la función 𝐹 con ellas misma 𝑘 veces.
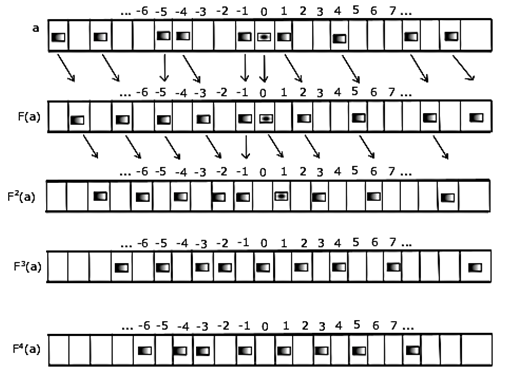
Cuando 𝑑=1,el autómata celular ℤ,Σ,𝑉,𝜑 es unidimensional. Un ejemplo bastante didáctico para entender cómo funciona los AC para modelar el flujo vehicular es usando la famosa regla 184 propuesta por Wolfram (1983) y Wolfram (1984). Esta regla para poder ser modelada en un computador es necesario tomar una cantidad finita de celdas o células en el retículo unidimensional, y claro, una cantidad finita de iterados de la función 𝐹 que actualiza cada célula. El espacio de estados que toma cada célula es Σ= 0, 1 (0 para un espacio en blanco y 1 para representar un vehículo) y la vecindad a tomar es 𝑉= −1, 0, 1 . Las posibles configuraciones, que son 8, es el espacio Σ 𝑉 = 0 0 1 , 0 1 0 , 0 1 1 , 0 0 0 , 1 0 1 , 1 1 0 , 1 1 1 , (1 0 0) y la función o regla local que rige los cambios para determinar el nuevo estado de cada célula es 𝜑: Σ 𝑉 → Σ, donde (4)
Luego, dada una configuración inicial 𝑎∈ Σ ℤ la transición de cada célula a la siguiente por la aplicación global 𝐹: Σ ℤ 𝑑 → Σ ℤ 𝑑 queda definida como: para cada posición 𝑖 de la célula, su actualización es 𝐹 𝑎 𝑖 =𝜑( 𝑎 𝑖−1 𝑎 𝑖+0 𝑎 𝑖+1 ). La regla local además de ver el estado actual de la célula, depende de sus vecinos inmediatos, anterior y siguiente. Se cambia el valor de 1 por un rectángulo pequeño en negro en la célula y un rectángulo en blanco para el 0. En la figura 1 se presenta un ejemplo con 22 células o celdas, donde el tiempo evoluciona de arriba hacia abajo.
Modelo de Nagel & Schreckenberg
En los inicios de los años 90 el modelo conocido como NaSch se popularizó debido a su facilidad para generar unas reglas simples de modelación del complicado tráfico usando autómatas celulares.
En esta subsección se ofrece una corta explicación del modelo. Ellos consideran un AC unidimensional ℤ 𝐿 ,Σ,𝑉, 𝜑 , donde se toma un subconjunto finito de células por ejemplo una cantidad 𝐿 y para la configuración inicial se toma Σ= 0, 1 como conjunto de estados. También, se considera la vecindad como el siguiente conjunto:
Lo interesante aquí es la regla de transición 𝜑 que no es fija, es variable en cada actualización ya que considera un parámetro probabilístico relacionado a la desaceleración del vehículo, es decir, cada célula al ser actualizada, puede desacelerar dependiendo del parámetro de probabilidad incluido 𝑝∈ 0, 1 . En realidad 𝜑 es una sucesión de reglas de transición 𝜑= 𝜑 𝑛 probabilística.
Para la implementación computacional e interpretación en ingeniería, el modelo es como sigue: considere una vía dividida en 𝐿 células todas del mismo tamaño de 7.5m, con una estructura topológica tipo redondel donde la primera célula se conecta con la última célula, no se puede adelantar y el avance del vehículo depende del vehículo del frente. La velocidad máxima de un vehículo es igual a 5, esto es, puede avanzar máximo 5 células y se denota 𝑣 𝑀 . El espacio entre vehículos se denota por 𝜀. Para iniciar el proceso es necesario tener una configuración inicial la cual va a depender de la cantidad de vehículos en la vía, esto es la densidad vehicular 𝜌= 𝐶𝑎𝑛𝑡𝑖𝑑𝑎𝑑 𝑑𝑒 𝑣𝑒ℎí𝑐𝑢𝑙𝑜𝑠 𝐿 y una probabilidad de desaceleración 𝑝∈ 0, 1 .
El modelo considera como 1 en la posición donde existe un vehículo y 0 para un espacio vacío. Si 𝑣 es la velocidad de un vehículo cualquiera en el estado actual entonces, la velocidad o el avance que va a tener un vehículo del siguiente tiempo se calcula siguiendo las siguientes condiciones:
- Si 𝑣< 𝑣 𝑀 y 𝑣<𝜀, entonces la velocidad del vehículo se actualiza a 𝑣+1.
- Si 𝑣>𝜀, entonces la velocidad se actualiza a el valor de 𝜀.
- Para cada célula se genera un número aleatorio 𝑑∈ 0, 1 . Si 𝑑<𝑝 y 𝑣>0 entonces, la velocidad se actualiza a 𝑣−1.
- El vehículo avanza a la velocidad actualizada.
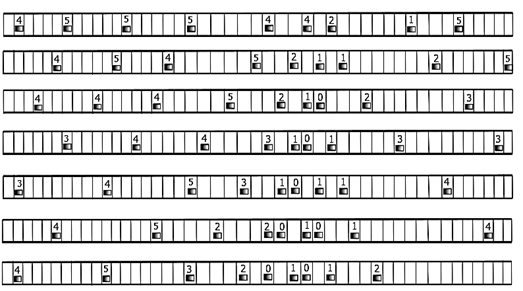
Exactamente el tercer punto es el que marcó la diferencia entre los modelos existentes para la época, haciendo que bajo ciertas configuraciones para la densidad y 𝑝, el modelo se adapte bien a las observaciones reales. Al pasar de los años todavía se sigue estudiando este modelo considerando las mismas reglas, variando valores de 𝑝, la longitud del conjunto de células y diferentes densidades de vehículos para una configuración inicial dada. A continuación, se muestra un ejemplo del modelo de NaSch para 46 células de la misma longitud, probabilidad de desaceleración 𝑝=0.5 y densidad 𝜌= 9 46 . La configuración inicial es la primera fila y el tiempo avanza de arriba hacia abajo, ver figura 2.
Revisión y discusión
Los modelos matemáticos se han utilizado para entender el comportamiento de diversos fenómenos de la naturaleza y la sociedad. El estudio del flujo del tráfico (FT) no escapa de esto. En la década de 1930 se comenzaron a plantear los primeros modelos matemáticos para describir y entender el comportamiento del flujo del tráfico usando el método de fotografías (Greenshields, 1934; Greenshields, 1935). A partir de este punto se comienza el estudio usando diferentes técnicas o modelos. Según Maerivoet y De Moor (2005) el estudio del flujo del tráfico se divide en 3 modelos fundamentales:
- Modelo Macroscópico
- Modelo Mesoscópico o Cinético
- Modelo Microscópico
Históricamente se han usado los modelos microscópicos para entender de forma global o de forma macroscópica el estudio del flujo vehicular enfocados en las interacciones de los modelos microscópicos, es decir, en las pequeñas interacciones que puede tener cada vehículo con su entorno y con las formas de manejo particular. Este tipo de estudios o modelo comenzó en la década de 1950, con varios trabajos realizados por diferentes autores en paralelo, con un modelo llamado car-following que considera la posición del vehículo, la velocidad y la aceleración, es un modelo a tiempo continuo donde los modelos matemáticos comenzaron siendo movimientos lineales luego, ecuaciones diferenciales de primer orden y segundo orden.
Para una revisión más detallada sobre los trabajos realizados en los años 50’s pueden consultarse Chandler, Herman, y Montroll (1958) y Gazis, Herman y Rothery (1961). Claro está, que este tipo de modelo, para la época era complicado realizar simulaciones computacionales debido a la naturaleza del modelo. Años después aparece lo que se convertiría en un modelo popular y relativamente simple para explicar el FV: el Modelo de Autómatas Celulares (MAC) también conocido en inglés como Traffic Cellular Automata (TCA). Ya que este modelo de tiempo discreto y espacio de fase discreto presentaba una forma sencilla de programar las simulaciones computacionales para describir un problema complicado como lo es el flujo vehicular. Wolfram (1984), en su clasificación de los AC como modelos matemáticos de Sistemas Dinámicos Discretos, propone un modelo simple unidimensional de AC para el flujo del tráfico con su famosa regla 184.
Más tarde a principios de 1990, un grupo de investigadores (Biham, Middleton y Levine 1992), publican un modelo bidimensional (de dos carriles), donde los vehículos de un carril circulan de forma contraria a los vehículos del otro carril y los vehículos dispuestos de forma aleatoria en la red del modelo. Ambos modelos hasta entonces se trabajan con AC determinístico. Paralelamente en el mismo año 92, otro modelo fue el presentado por Nagel y Schreckenberg, el primer modelo no trivial de un AC probabilistico.
De estos trabajos sobresale el trabajo de NaSch ya que al compararlos con modelos reales se obtuvieron resultados bastantes favorables, lo que rápidamente popularizó el modelo y comenzó a aplicarse en las calles de varias ciudades grandes en distintos países. Como se observó en la sección 3, este modelo de NaSch se presta para diferentes modificaciones. Por ejemplo, si observa el modelo del ejemplo de la figura 2, se puede pasar de 135km/h de 25 a 30 km/h, lo cual es un frenado brusco e imposible de realizar.
En lo que sigue de la sección, la concentración se enfoca en los modelos de autómatas celulares para el FV dependiendo de la cantidad de carriles en la vía. Un carril y dos carriles o múltiples carriles.
Modelos de un carril
En estudios posteriores al modelo de NaSch, se considera el papel del parámetro de frenado o desaceleración 𝑝 para una vía rápida de un carril, si el valor de 𝑝 es muy alto (la probabilidad de desaceleración del vehículo es alta), siempre se tendrán atascos o flujo de tráfico lento a menos que la densidad del número de vehículos sea pequeña en un tramo largo de la vía y la desaceleración la absorba la distancia entre los vehículos. En los trabajos Schadschneider (1999), Schadschneider (2002) y Nagel (1994) se detallan modelos para explicar la influencia del parámetro de frenado 𝑝. En Schreckenberg, Barlović, Knospe, y Klüpfel, (2002) se estudia cómo afecta el flujo del tráfico cuando la densidad de carros es alta.
Entre tantos modelos y reglas impuestas a las interacciones entre los vehículos para que la modelación matemática sea lo más adaptada a la realidad del FV, existe una regla llamada de inicio lento (en inglés slow-to-star rule) la cual ha sido usada en la literatura como modelo BJH. En principio fue propuesta para modelar el flujo en una vía que se incorpora a una autopista donde los vehículos reducen bastante la velocidad al punto de casi detenerse y luego comenzar a aumentar la velocidad progresivamente (Benjamin, Johnson, & Hui, 1996). Siguiendo este modelo se han realizado varios estudios sobre todo la forma de manejo del conductor, cuando desacelera y acelera por algún motivo, que puede ser generado por algún imprevisto en la vía o por decisión del conductor. Lárraga y Alvarez-Icaza (2010), estudian este caso de aceleración, desaceleración o velocidad constante en una vía, manteniendo el espacio promedio intervehicular y las limitaciones que ofrece el vehículo del frente para hacer el modelo un poco más realista, por ejemplo, cuando un grupo de vehículos se acerca a un embotellamiento. En cambio, Guzmán, Lárraga, Alvarez-Icaza y Carvajal (2018) estudian los movimientos de aceleración y desaceleración uniforme y no impulsivo. Cuando un vehículo va al frente (vehículo líder) de un grupo de vehículos en una vía de un carril la forma de conducir del vehículo líder, sobre todo en el aspecto de acelerar y desacelerar, determina el flujo del tránsito.
Este fenómeno se puede ver en forma real y dinámica con múltiples vídeos en la dirección electrónica de la siguiente referencia (De camino. 2016; Smartmotoris, 2019). Aunque el resultado ya es conocido, el video es interesante, porque ayuda a entender cómo una pequeña decisión del conductor del vehículo líder afecta al FV.
Los modelos de un carril por lo general se estudian considerando condiciones de frontera cerrada, aunque existen modelos con frontera abierta, abierta con condiciones y abierta infinita, consideras en Matemáticas.
El artículo de Maerivoet y De Moor (2005) hace un buen seguimiento a los trabajos con AC para la época describiendo principalmente los modelos para un carril aunque trata los de dos carriles y múltiples carriles. También, presenta las reglas impuestas al sistema para obtener modelos para diferentes condiciones de manejos y condiciones de la vía. Los casos de modelos de tráfico heterogéneo son estudiados en este artículo. Muchos de los trabajos realizados recientemente se han hecho para uno y varios carriles los cuales serán presentados en la siguiente sección.
Modelos con dos y múltiples carriles
Como ya se había mencionado antes, paralelamente al modelo de NaSch, se presentó un modelo de dos vías usando AC (Biham, Middleton, & Levine, 1992). En este modelo los vehículos de un carril circulan de forma contraria al del otro carril, este tipo de vías es común en las principales carreteras del Ecuador.
Es importante notar que los modelos con dos o múltiples carriles son más difíciles de analizar y modelar, por la presencia de más variables y porque las probabilidades de colisión son mayores. Para estos modelos el conductor no sólo debe estar atento al carro del frente y de atrás sino a los vehículos próximos a él en los otros carriles laterales, sobre todo si desea hacer un adelantamiento.
Los modelos con dos carriles, claro está, aparecerían tan pronto se comenzó a estudiar los de un carril. Las primeras modificaciones a dos carriles del modelo NaSch, según se encontró en la literatura, son las dadas por Rickert, Nagel, Schreckenberg y Latour (1996) y Wagner, Nagel y Wolf (1997); el último incluye un estudio para múltiples carriles. Luego de estos trabajos, aparece un interesante artículo de Nagel, Wolf, Wagner y Simon (1998), que presenta vías de dos carriles con vehículos circulando en la misma dirección, además una serie de reglas para diferentes modelos al caracterizar el cambio de carril de los vehículos. Las variables seguidas corresponden a, la velocidad del vehículo conducido, la velocidad del vehículo de adelante, la velocidad del vehículo de atrás y de los vehículos próximos de los carril derecho o izquierdo, en dependencia de la maniobra a realizar por cambio de carril. Es importante resaltar que en la publicación de Nagel et al. (1998), muestra y comprara las variables de velocidad y espacio entre los vehículos para realizar el cambio de carril.
Más tarde, en el trabajo Rawat, Katiyar y Gupta (2012), se hace una corta pero bien presentada exposición de los modelos con dos carriles inducidos por los diferentes modelos de un carril. En otros estudios, se han ido cambiando las reglas de los modelos a medida que se van obteniendo datos reales del comportamiento del tráfico. Un ejemplo es el observado en la India donde no hay una disciplina apropiada en los conductores para el cambio de carril (Mallikarjuna & Rao, 2011). El caso de tráfico heterogéneo como el de la India existe en otros países, pueden encontrarse estudios donde se incluyen ciclistas en la vía y carriles asimétricos (Nassab, Schreckenberg, Ouaskit, & Boulmakoul, 2005). En Pandey, Rao y Mohan (2015) se estudia el tráfico heterogéneo incluyendo la existencia de ciclistas en la vía con la diferencia que propone un estudio para vías asimétricas. Entre tantas inclusiones para un tráfico no homogéneo también se ha pensado en incluir motocicletas, donde la velocidad es diferente al de una bicicleta y en la vía puede ir en un carril lento o en un carril rápido, lo que no sucede con las bicicletas (Meng, Dai, Dong, & Zhang, 2007).
Varios trabajos presentan no solo sus ideas para vías con dos carriles sino para 3 y hasta 6 carriles aunado a esto se incluyen las condiciones en la vía, por ejemplo, una vía con 3 carriles y un grado de inclinación donde circulan vehículos de carga pesada de 6 ejes a baja velocidad, lo que hace obtener flujo lento y mayor dificultad para adelantar. Un trabajo reciente sobre este tipo de modelo fue el realizado por Yang, Zheng, Cheng y Ran (2019), para una autopista en China. No siempre se encuentran conductores que cumplan las normas de seguridad para hacer un adelantamiento adecuado, sino todo lo contrario, existen conductores que lo hacen de forma agresiva (Li, Jia, Gao, & Jiang,, 2006). En el momento menos esperado se pueden encontrar en la vía un incidente que genera inmediatamente la paralización total de la vía o un embotellamiento si queda algún carril por donde se pueda circular.
Los modelos presentados por Zhu, Lei y Dai (2009) han sido considerados en este trabajo. Algo común en muchas ciudades es el stress causado en los conductores por el FV, quienes no dudan en tocar la bocina una y otra vez causando un stress mayor, incomodando al peatón y contribuyendo a la contaminación de ruido. Este caso también ha sido estudiado observando el efecto generado por el bocinado en vías de dos carriles (Jia, Jiang, Wu, & Hu, 2005).
Recientemente usando el avance de las telecomunicaciones y la electrónica se han estudiado modelos que incluyen reglas donde el vehículo entra en una zona donde existe internet de vehículos, IoV (Zhao, Liu, Chen, & Lu, 2018). El IoV considera interacciones del vehículo con la infraestructura de la vía, interacciones entre los vehículos e interacciones del vehículo con el peatón (Maglaras, Al-Bayatti, He, Wagner, & Janicke, 2016). Se cree que este tipo de modelos comenzará a crecer debido al auge de las telecomunicaciones y la conectividad de los vehículos y de las vías. Además, la inevitable llegada de los autos eléctricos que presentan una mayor conectividad que los actuales.
Conclusiones
En esta revisión se puede concluir que con el pasar del tiempo, los modelos o problemas considerados en el estudio de flujo vehicular se han ido adaptando a las condiciones del tráfico del momento. Las grandes ciudades son las que nutren de ideas a los investigadores para realizar nuevos modelos no considerados hasta el momento, como por ejemplo los modelos presentados en Zhao y colaboradores (2018) para vehículos y vías con internet.
El modelo de un carril de Nagel y Schreckenberg (1992), permite agregar o modificar reglas de interacción, considerar la infraestructura de la vía como por ejemplo cruces, semáforos, instrumentos de reducción de velocidad, entre otras interrogantes observadas en los modelos de flujo de tráfico.
En el estudio se percibió que los cambios en la conducta del conductor se han ido incorporando en los modelos de autómatas celulares. Tales modelos pueden ser estudiados y aplicados en las vías del Ecuador en ciudades de tamaño mediano a pequeño, como por ejemplo, Ambato, Portoviejo y Riobamba, debido a que en estas ciudades existe un FV importante.
Cabe destacar que los modelos con múltiples carriles son de naturaleza compleja. Los estudios de estos modelos se encuentran con mayor frecuencia en Estados Unidos, países europeos y asiáticos, y escasamente en países del sur de América. Durante la revisión de la literatura no se encontraron estudios o propuestas para vías de dos carriles para uso del transporte urbano y que cuenten con espacios para recoger pasajeros. Este escenario es común en algunas vías de los países de América del sur, por lo que las propuestas de modelado del FV tendrían resultados interesantes.
En el trabajo se presentó el modelo determinístico de los autómatas celulares con sus elementos formales matemáticamente, pero que no describe el modelo de NaSch. El próximo estudio es presentar el modelo probabilístico de autómatas celulares desde la formalidad matemática describiendo cada uno de sus elementos que lo modelan y así describir formalmente el modelo de NaSch.
Conflicto de Interés
Los autores declaramos que no existe conflicto de interés de naturaleza alguna.
Agradecimiento
El autor Ruiz Luis B. agradece el apoyo brindado al Vicerrectorado de Postgrado, Investigación y Vinculación de la Universidad Nacional de Chimborazo (UNACH), ya que parte del trabajo fue desarrollado durante su estadía en dicha institución. A la profesora Ligia Araque Mora, por sus buenas sugerencias y correcciones para que el artículo siguiera el formato correctamente.