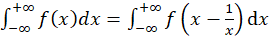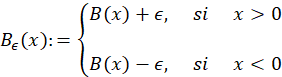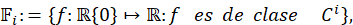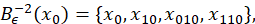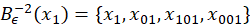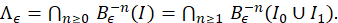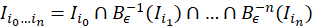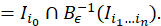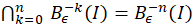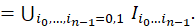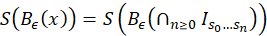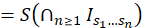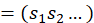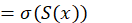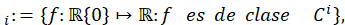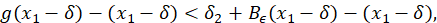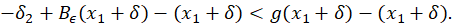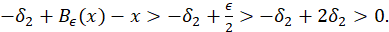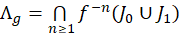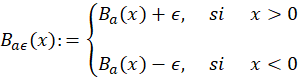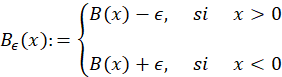1 Introducción
La historia de la transformación de Boole comienza en 1857, cuando George Boole prueba que la función 𝐵:ℝ\{0}⟶ℝ dada por 𝐵(𝑥)=𝑥− 1 𝑥 preserva la medida de Lebesgue y descubre la sorprendente fórmula (ecuación 1):
es verdadera para cualquier función 𝑓:ℝ⟶ℝ Riemann integrable (Boole, 1857). Tal función hoy en día es conocida como transformación de Boole. Más tarde, (Adler & Weiss, 1973), demuestran que, 𝐵 es ergódica respecto a la medida de Lebesgue. Es este un hecho interesante, debido a que existen diferencias fundamentales entre espacios de medida infinita y espacios de medida finita. Después de lo cual, varios autores han trabajado en las propiedades ergódicas de parametrizaciones de 𝐵, algún tipo de generalización y en transformaciones que preservan medidas infinitas (Aaronson, 2007, Aaronson, 1983, Neuwirth, 1978, Prykarpatsky & Feldman, 2006). Hasta aquí el estudio de esas aplicaciones, ha sido de tipo ergódico y no sobre las propiedades de dinámica topológica como el conjunto de puntos periódicos y transitividad, este último importante en el concepto de caos dinámico; aunque recientemente en Muñoz (2015) se presentan condiciones para las que, una clase de familias con propiedades parecidas a la transformación de Boole, sea transitiva.
En Prykarpatsky & Feldman (2006) se estudia la ergodicidad de familias parametrizadas de la transformación B, una de esas es de la forma 𝐵 𝑎𝜖 (𝑥)=𝑥− 𝑎 𝑥 +𝜖, para 𝑎>0 y 𝜖>0. También se demuestra que preserva una medida infinta, pero no es ergódica respecto a esa medida. Lo anterior no significa que está todo perdido. Aquí consideramos un modelo geométrico de la transformación de Boole y probaremos algunas propiedades dinámicas para un tipo de traslación o parametrización de dicho modelo geométrico que posee las principales propiedades de la transformación de Boole, que llamaremos tipo Boole, como se puede apreciar en la siguiente definición:
Definición 1.1 Una transformción 𝐵:ℝ\{0}⟶ℝ de clase 𝐶 1 es tipo Boole si
𝐵′(𝑥)>1 para todo 𝑥;
lim 𝑥→ 0 + 𝐵(𝑥)=−∞ y lim 𝑥→ 0 − 𝐵(𝑥)=+∞;
𝐵(𝑥)≠𝑥 para todo 𝑥;
lim 𝑥→+∞ 𝐵(𝑥)−𝑥 =0 y lim 𝑥→−∞ 𝐵(𝑥)−𝑥 =0
La traslación (o parametrización) de 𝐵 de la que se ha venido mencionando, viene dada por la forma mostrada en 2, en donde para cada 𝜖∈ℝ, se define
De aqui en adelante esta transformación será referida como FTB.
En concreto se prueba lo siguiente:
Teorema 1.2 Si 𝐵 es una transformación tipo Boole entonces, para cada 𝜖>0, existe un conjunto cantor 𝛬 𝜖 invariante respecto a la transformación 𝐵 𝜖 , tal que 𝐵 𝜖 | 𝛬 𝜖 es transitiva y su conjunto de puntos periódicos es denso en 𝛬 𝜖 . Además, si 𝑥∈ 𝛬 𝜖 𝑐 se tiene que, | 𝐵 𝑛 (𝑥)|→+∞ cuando 𝑛→+∞.
En el estudio de los fenómenos dinámicos, es muy interesante saber si ellos son persistentes bajo perturbaciones, una forma de persistencia significa que al perturbar, el nuevo sistema obtenga algunas caracteristicas del sistema original, como por ejemplo propiedades dinámicas (los mismos puntos periódicos, transitividad). Dado el siguiente conjunto (ecuación 3):
para 𝑖=0, 1, 2.
Diremos que 𝑔∈ 𝔽 0 es 𝛿− 𝐶 0 próximo de 𝐵 𝜖 si |𝑔(𝑥)− 𝐵 𝜖 (𝑥)|<𝛿 para todo 𝑥≠0. También, diremos que 𝑔∈ 𝔽 1 es 𝛿− 𝐶 1 próximo de 𝐵 𝜖 si 𝑔 es 𝛿− 𝐶 0 próximo de 𝐵 𝜖 y |𝑔′(𝑥)− 𝐵′ 𝜖 (𝑥)|<𝛿 para todo 𝑥≠0. Sea 𝑓∈ 𝔽 1 tal que 𝑓 posee un conjunto de cantor Λ 𝑓 invariante y transitivo. Diremos que 𝑓 es robustamente transitivo si existe 𝛿>0 tal que si 𝑔∈ 𝔽 1 es 𝛿− 𝐶 1 próximo de 𝑓, 𝑔 posee un conjunto de cantor Λ 𝑔 invariante transitivo y 𝑔 | Λ 𝑔 es topológicamente conjugado a 𝑓 | Λ 𝑓 , lo último significa que existe un homeomorfismo ℎ: Λ 𝑔 ⟶ Λ 𝑓 tal que 𝑓∘ℎ(𝑥)=ℎ∘𝑔(𝑥) para todo 𝑥∈ Λ 𝑔 .
Teorema Principal 1 Sea 𝐵 una transformación tipo Boole. Para cada 𝜖>0, la transformación 𝐵 𝜖 es robustamente transitiva.
2 Metodología
En la revisión bibliográfica se pudo constatar que existe muy poco avance en el estudio de la dinámica topológica, como lo son puntos periódicos, transitividad, robustez transitiva, etc., en las parametrizaciones de la transformación de Boole. Aunque, sí encontramos que existen estudios desde el punto de vista de la teoría ergódica.
En la familia de traslaciones de la transformación tipo Boole, usamos el método tradicional para la construcción de conjuntos de Cantor, estos métodos se pueden encontrar desarrollados en Devaney (1989) y Robinson (1999). Adaptamos esos métodos, con cierto cuidado ya que las transformaciones tipo Boole poseen una asíntota vertical, para mostrar que Λ 𝐵 𝜖 es un conjunto de Cantor invariante para todo 𝜖>0. Para probar que Λ 𝐵 𝜖 es transitiva respecto a 𝐵 𝜖 para todo 𝜖>0, usamos un método bastante tradicional en sistemas dinámicos que propone conseguir una conjugación topológica (ver parte final de la introducción para su definición) entre 𝐵 | Λ 𝐵 𝜖 y el shift unilateral 𝜎 (ver inicio de la demostración del Teorema 1.2 para su definición).
Para considerar el modelo geométrico de la transformación de Boole, lo que hicimos fue considerar su diferenciabilidad, por lo menos exigir que sea de clase 𝐶 1 , su derivada mayor que 1 para todos los puntos del dominio, considerar sus dos asíntotas, la vertical en 𝑥=0 y la asíntota oblicua en 𝑦=𝑥 y finalmente pedirle que no tenga puntos fijos, ver definición 1.1.
Para obtener el Teorema principal, el método usado fue descifrar lo hecho en Robinson (1999) para la función logística y lo hecho en Muñoz (2015), para transformaciones no acotadas con una discontinuidad, adaptarlo a nuestro caso, de manera que las perturbaciones 𝛿- 𝐶 1 próximas a 𝐵 𝜖 obtuvieran puntos fijos hipebólicos, es decir, puntos fijos con derivada estrictamete mayor que 1, además las perturbaciones se realizan dentro del espacio de las transformaciones 𝐶 1 con una discontinuidad en 𝑥=0.
3 Resultados y Discusión
Comenzaremos con algunos resultados preliminares y notación básica necesaria para alcanzar nuestro objetivo.
3.1 Preliminares
Considere la traslación de una transformación tipo Boole 𝐵, (ecuación 4)
observe que las restricciones sobre cada componente conexa es un difeomorfismo de clase 𝐶 1 sobre ℝ, es decir, 𝐵 −𝜖 | (−∞,0) :(−∞,0)↦ℝ y 𝐵 +𝜖 | (0,+∞) :(0,+∞)↦ℝ, son difeomorfismos crecientes de clase 𝐶 1 . La siguiente observación de funciones derivables será de utilidad en este trabajo.
Observación 3.1 Sea 𝐽 un intervalo y 𝑓:𝐽⊂ℝ↦ℝ derivable tal que 𝑓′(𝑥)>1, para todo 𝑥∈𝐽. Si existe 𝑥 0 ∈𝑖𝑛𝑡(𝐽) y 𝑓( 𝑥 0 )= 𝑥 0 , entonces
??(𝑥)>𝑥, ∀ 𝑥> 𝑥 0 , con 𝑥∈𝐽;
𝑓(𝑥)<𝑥, ∀ 𝑥< 𝑥 0 , con 𝑥∈𝐽
Puntos fijos
Por la observación 3.1, 𝐵 𝜖 posee sólo dos puntos fijos, uno 𝑥 0 ∈(−∞, 0) y el otro 𝑥 1 ∈(0, +∞). Ahora, existe 𝑥 01 ∈( 𝑥 0 , 0) tal que 𝐵 −𝜖 ( 𝑥 1 )= 𝑥 01 y existe 𝑥 01 ∈(0, 𝑥 1 )) tal que 𝐵 +𝜖 ( 𝑥 0 )= 𝑥 01 . Denotado por 𝐼 0 =[ 𝑥 0 , 𝑥 01 ]⊂(−∞,0), 𝐼 1 =[ 𝑥 10 , 𝑥 1 ]⊂(0,+∞) y 𝐼=[ 𝑥 0 , 𝑥 1 ].
Observació 3.2 Ya que 𝐵′(𝑥)>1 para todo 𝑥≠0, se tiene que 𝐵 −𝜖 | 𝐼 0 : 𝐼 0 ⟼𝐼 y 𝐵 +𝜖 | 𝐼 1 : 𝐼 1 ⟼𝐼 son homeomorfismos.
Notación 3.3 los puntos 𝑥 01 y 𝑥 10 poseen sus respectivas preimagenes en la siguiente iteración, denotaremos por 𝑥 110 a la preimagen positiva de 𝑥 10 y 𝑥 010 a la preimagen negativa de 𝑥 10 , esto es, 𝐵 +𝜖 −1 ( 𝑥 10 )= 𝑥 110 y 𝐵 −𝜖 −1 ( 𝑥 10 )= 𝑥 010 , por lo tanto 𝐵 𝜖 −1 ( 𝑥 10 )={ 𝑥 110 , 𝑥 010 }.
Similarmente; (ecuación 5 y ecuación 6) denotaremos por 𝑥 101 a la preimagen positiva de 𝑥 01 y 𝑥 001 a la preimagen negativa de 𝑥 01 , esto es 𝐵 +𝜖 −1 ( 𝑥 01 )= 𝑥 101 y 𝐵 −𝜖 −1 ( 𝑥 01 )= 𝑥 001 , así 𝐵 𝜖 −1 ( 𝑥 01 )={ 𝑥 001 , 𝑥 101 }, por lo que:
Siguiendo la notación, en general dado un punto eventualmente fijo 𝑥 𝑖 1 … 𝑖 𝑘 , la referencia ?? 0 correspondiente a su preimagen negativa será 𝑖 0 =0 y para la correspondiente preimagen positiva será 𝑖 0 =1, es decir, 𝐵 −𝜖 −1 𝑥 𝑖 1 … 𝑖 𝑘 = 𝑥 0 𝑖 1 … 𝑖 𝑘 y 𝐵 +𝜖 −1 𝑥 𝑖 1 … 𝑖 𝑘 = 𝑥 1 𝑖 1 … 𝑖 𝑘 donde 𝑖 𝑗 =0:1 para 𝑗=1:𝑘.
Proposición 3.4 Si 𝐴=[ 𝑥 0 , 𝑥 1 ] 𝑐 = 𝐼 𝑐 , entonces 𝐵 𝜖 (𝐴)⊂𝐴 y para cada 𝑥∈𝐴 se tiene que, | 𝐵 𝜖 𝑛 (𝑥)|→+∞, cuando 𝑛→+∞.
Proof. La primera parte se basa en la observación 3.1.
Para la segunda parte, sea 𝑥∈( 𝑥 1 , +∞), del hecho que 𝐵′ +𝜖 (𝑥)>1, para todo 𝑥∈ℝ\{0} y de la observación 3.1 se concluye que 𝐵 +𝜖 (𝑥)>𝑥. Luego, iterando 𝑥 respecto a 𝐵 +𝜖 se sigue que, 𝐵 +𝜖 (𝑥)< 𝐵 +𝜖 2 (𝑥) e iterando sucesivamente se tiene que 𝐵 +𝜖 𝑛 (𝑥)< 𝐵 +𝜖 𝑛+1 (𝑥), para todo 𝑛>0, es decir, { 𝐵 +𝜖 𝑛 (𝑥) } 𝑛=1 +∞ es una sucesión monótona creciente. Ya que 𝐵 +𝜖 tiene un único punto fijo en (0, +∞), que es 𝑥 0 . Entonces, 𝐵 +𝜖 𝑛 (𝑥)→+∞, cuando 𝑛→+∞. El caso 𝑥∈(−∞, 𝑥 0 ) es completamente análogo. (ecuación 7)
Sea,
Proposición 3.5 Si 𝜖>0. Si 𝑥∈ 𝛬 ?? 𝑐 \( ∪ 𝑛≥0 𝐵 𝜖 −𝑛 (0)), entonces | 𝐵 𝜖 𝑛 (𝑥)|→+∞, cuando 𝑛→+∞.
Proof. Sea 𝑥∈ Λ 𝜖 𝑐 ( ∪ 𝑛≥0 𝐵 𝜖 −𝑛 (0)), entonces existe un 𝑗∈ℕ tal que 𝐵 𝜖 𝑗 (𝑥)∈𝐴, aplicando la proposición 3.4 se sigue facilmente la prueba.
De la proposición 3.4, la observación 3.2 y la proposición 3.5, la dinámica interesante de la transformación 𝐵 𝜖 está contenida en el intervalo 𝐼=[ 𝑥 0 , 𝑥 1 ].
Notación 3.6 Recordemos que
𝑥 0 < 𝑥 001 < 𝑥 010 < 𝑥 01 <0 y 𝑥 10 < 𝑥 101 < 𝑥 110 < 𝑥 1 , ahora bien denotemos por 𝐼 00 =[ 𝑥 0 , 𝑥 001 ], 𝐼 01 =[ 𝑥 010 , 𝑥 01 ], ?? 10 =[ 𝑥 10 , 𝑥 101 ] y 𝐼 11 =[ 𝑥 110 , 𝑥 1 ], tales intervalos 𝐼 𝑖 0 𝑖 1 son aplicados difeomorficamente sobre 𝐼 𝑖 1 . En consecuencia, 𝐵 𝜖 −1 ( 𝐼 0 )= 𝐼 00 ∪ 𝐼 10 y 𝐵 𝜖 −1 ( 𝐼 1 )= 𝐼 01 ∪ 𝐼 11 , posteriormente 𝐵 𝜖 −2 (𝐼)= 𝐼 00 ∪ 𝐼 01 ∪ 𝐼 10 ∪ 𝐼 11 , es la unión disjunta de 2 2 intervalos compactos. Por otro lado observe que 𝐼 𝑖 0 ∩ 𝐵 𝜖 −1 ( 𝐼 𝑖 1 )= 𝐼 𝑖 0 𝑖 1 con 𝑖 0 , 𝑖 1 ∈{0,1}, luego como 𝐵 𝜖 ( 𝐼 𝑖 0 )=𝐼, entonces 𝐵 𝜖 ( 𝐼 𝑖 0 𝑖 1 )= 𝐵 𝜖 ( 𝐼 𝑖 0 ∩ 𝐵 𝜖 −1 ( 𝐼 𝑖 1 ))= 𝐵 𝜖 ( 𝐼 𝑖 0 )∩ 𝐼 𝑖 1 = 𝐼 𝑖 1 y en general: (ecuación 8), (ecuación 9)
Para mostrar que Λ 𝜖 es un conjunto de cantor, seguiremos de cerca las ideas desarrolladas en Devaney (1989) y Robinson (1999). Con la notación que traemos hasta aquí, los siguientes dos lemas, lema 3.7 y lema 3.8 se encuentran en Devaney (1989), por tal razón omitimos la demostración.
Lema 3.7 Para todo 𝑛∈ℕ se tiene que: (ecuación 10), (ecuación 11)
Lema 3.8 Para cada iteración 𝑛≥2 de la FTB, valen las siguiente propiedades:
Para cualquier elección 𝑖 0 … 𝑖 𝑛−2 ∈{0,1}, tenemos que:
Para dos elecciones distintas digamos ( 𝑖 0 … 𝑖 𝑛−1 )≠( 𝑖′ 0 … 𝑖′ 𝑛−1 ), tenemos que: 𝐼 𝑖 0 … 𝑖 𝑛−1 ∩ 𝐼 𝑖′ 0 … 𝑖′ 𝑛−1 =∅; es decir, 𝐵 𝜖 −𝑛 (𝐼) es la unión de 2 𝑛 intervalos cerrados disjuntos.
𝐵 𝜖 aplica la componente 𝐼 𝑖 0 … 𝑖 𝑛−1 ⊂ 𝐵 𝜖 −𝑛 (𝐼) homeomorficamente sobre el intervalo 𝐼 𝑖 1 … 𝑖 𝑛−1 ⊂ 𝐵 𝜖 −𝑛+1 (𝐼)
Lema 3.9 Si
𝜆:= inf 𝐵 𝜖 ′ 𝑥 :𝑥∈ 𝐼 0 ∪ 𝐼 1 >1, entonces 𝐿( 𝐼 𝑖 0 … 𝑖 𝑛−1 )≤ 𝜆 −𝑛 ( 𝑥 1 − 𝑥 0 ) para cualquier elección 𝐼 𝑖 0 … 𝑖 𝑛−1 ⊂ 𝐵 𝜖 −𝑛 (𝐼).
Proof. Considere una elección 𝐼 𝑖 0 … 𝑖 𝑛−1 ⊂ 𝐵 𝜖 −𝑛 (𝐼). Luego, por el lema 3.8 se tiene que, 𝐼 𝑖 0 … 𝑖 𝑛−1 ⊂⋯ 𝐼 𝑖 0 𝑖 1 ⊂ 𝐼 𝑖 0 ⊂𝐼=[ 𝑥 0 , 𝑥 1 ]. Usando el Teorema del Valor Medio, se tiene que 𝐿( 𝐼 𝑖 0 )< 𝜆 −1 ( 𝑥 1 − 𝑥 0 ). Aplicando sucesivamente esto a los siguientes intervalos de la elección se sigue el resultado.
Teorema 3.10 Si 𝐵 es tipo Boole y 𝜖>0, entonces 𝛬 𝜖 := 𝑥∈𝐼\ ∪ 𝑛≥0 𝐵 𝜖 −𝑛 0 : 𝐵 𝜖 𝑛 𝑥 ∈𝐼,∀𝑛∈ℕ es un conjunto de Cantor.
Proof. De la proposición 3.4 podemos notar que el conjunto Λ 𝜖 ⊂ 𝐼 0 ∪ 𝐼 1 .
1)Para verificar que Λ 𝜖 es compacto basta notar que el lema 3.7 nos dice que Λ 𝜖 es intersección numerable de intervalos compactos encajados. Entonces, Λ 𝜖 es compacto.
2)Probemos que Λ 𝜖 es totalmente disconexo. Notemos que 𝜆 −𝑘 ( 𝑥 1 − 𝑥 0 )→0, cuando 𝑘→∞. (∗)
Ahora, supongamos que Λ 𝜖 no es totalmente disconexo, es decir que existe un intervalo 𝐽⊂ Λ 𝜖 = 𝑛=0 +∞ 𝐵 𝜖 −𝑛 𝐼 , luego por (∗) existe un 𝑛>1 tal que 𝜆 −𝑛 ( 𝑥 1 − 𝑥 0 )<𝐿(𝐽), además por el lema 3.7 tenemos que 𝐽⊂ 𝐵 𝜖 −𝑛 (𝐼)= 𝑖 0 ,…, 𝑖 𝑛−1 =0,1 𝐼 𝑖 0 … 𝑖 𝑛−1 , la cual por el lema 3.8 sabemos que es unión de intervalos disjuntos dos a dos. Por lo tanto existe una colección 𝑗 0 ,…, 𝑗 𝑛−1 ∈{0,1}, tal que 𝐽⊂ 𝐼 𝑗 0 … 𝑗 𝑛−1 , por el lema anterior (3.9), obtenemos que 𝐿 𝐽 ≤𝐿 𝐼 𝑗 0 … 𝑗 𝑛−1 ≤ 𝜆 −𝑛 𝑥 1 − 𝑥 0 , lo cual es una contradicción. Por lo tanto Λ 𝜖 no posee intervalos, en consecuencia Λ 𝜖 es totalmente disconexo.
3) La demostración de que Λ 𝜖 es perfecto, es igual a la realizada en el Teorema 4.1 en [Robinson, 1999].
En conclusión Λ ?? es un conjunto de Cantor.
3.2 Prueba de los resultados principales
Definiremos 𝛴 2 :={𝑠=( 𝑠 0 𝑠 1 … 𝑠 𝑗 …) : 𝑠 𝑗 ∈{0, 1} 𝑗∈ℕ}. Este conjunto es llamado el espacio de sucesiones de dos símbolos 0 y 1, diremos que una secuencia 𝑠 𝑖 … 𝑠 𝑗 es una “palabra”del espacio 𝛴 2 de longitud 𝑗−𝑖. Además, diremos que 𝑠,𝑡∈ 𝛴 2 son iguales (𝑠=𝑡), si ), 𝑗 = 𝑡 𝑗 para todo 𝑗∈ℕ.
Con la métrica 𝑑 𝑠,𝑡 = 𝑖=0 +∞ 𝑠 𝑖 − 𝑡 𝑖 2 𝑖 , es bien conocido que 𝛴 2 es un conjunto compacto. La función shift 𝜎: 𝛴 2 → 𝛴 2 esta definida como 𝜎( 𝑠 0 𝑠 1 𝑠 2 …)=( 𝑠 1 𝑠 2 𝑠 3 …). También, es bien conocido que 𝜎 es continua, el conjunto de punto periódicos es denso y trasitivo.
Proof. (Teorema 1).
Sea 𝐵 una trasformación tipo Boole, 𝜖>0 y sea 𝐵 𝜖 una traslación de 𝐵. Considere 𝑆: Λ 𝜖 ⟶ 𝛴 2 , para cada 𝑥∈ Λ 𝜖 , 𝑆(𝑥)= 𝑠 0 𝑠 1 𝑠 2 … donde 𝑠 𝑖 =0 si 𝐵 𝜖 𝑖 (𝑥)∈ 𝐼 0 y 𝑠 𝑖 =1 si 𝐵 𝜖 𝑖 (𝑥)∈ 𝐼 1 . 𝑆 es llamada el Itinerario de 𝑥. La idea es probar que 𝑆 es una conjungación topológica entre 𝜎 y 𝐵 𝜖 , de esta manera 𝐵 𝜖 tiene las mismas propiedadades dinámicas que 𝜎, es decir, 𝐵 𝜖 | Λ 𝜖 es transitiva y el conjunto de puntos periódicos son densos en Λ 𝜖 . Notemos que para todo 𝑥∈ Λ 𝜖 se tiene que 𝑥= 𝐼 𝑖 0 … 𝑖 𝑛 … y el itinerario de 𝑥 es precisamente 𝑆(𝑥)= 𝑖 0 … 𝑖 𝑛 ….
Inyectividad. Sean 𝑥,𝑦∈ Λ 𝜖 supongamos que 𝑆(𝑥)≠𝑆(𝑦), luego existe 𝑗∈ℕ tal que 𝐵 𝜖 𝑗 (𝑥) y 𝐵 𝜖 𝑗 (𝑦) están en diferentes componentes conexas, es decir, si 𝑆(𝑥)= 𝑖 0 … 𝑖 𝑗 … y 𝑆(𝑦)= 𝑖′ 0 … 𝑖′ 𝑗 … entonces, 𝑦∈ 𝐼 𝑖′ 0 … 𝑖′ 𝑗 y 𝑥∈ 𝐼 𝑖 0 … 𝑖 𝑗 , donde 𝑖 𝑗 ≠ 𝑖′ 𝑗 ; luego, por el lema 3.8 𝐼 𝑖′ 0 … 𝑖′ 𝑗 ∩ 𝐼 𝑖 0 … 𝑖 𝑗 =∅, así se concluye que 𝑥≠𝑦.
Sobreyectividad. Considere 𝑠∈ 𝛴 2 , recordemos lo siguiente: 𝐼 𝑠 0 … 𝑠 𝑛 = 𝐼 𝑠 0 ∩ 𝐵 𝜖 −1 ( 𝐼 𝑠 1 )∩…∩ 𝐵 𝜖 −𝑛 ( 𝐼 𝑠 𝑛 ); luego, existe 𝐼 𝑠 0 𝑠 1 … = ∩ 𝑘=0 +∞ 𝐼 𝑠 0 … 𝑠 𝑘 una sucesión encajada de intervalos compactos, donde 𝑠 𝑘 =0:1 para 𝑘≥0. Por lo tanto existe 𝑥∈ 𝐼 𝑠 = ∩ 𝑘=0 +∞ 𝐵 𝜖 −𝑘 ( 𝐼 𝑠 𝑘 ). En consecuencia, si 𝐵 𝜖 𝑘 (𝑥)∈ 𝐼 𝑠 𝑘 para todo 𝑘≥0, entonces 𝑆(𝑥)=𝑠.
Continuidad. Sea 𝑥∈ Λ 𝜖 y supongamos que 𝑆(𝑥)= 𝑠 0 … ?? 𝑛 …. Sea 𝜀′>0, luego existe 𝑛∈ℕ tal que 1 2 𝑛 <𝜀′ y consideremos el intervalo 𝐼 𝑠 0 … 𝑠 𝑛 y elijamos 𝛿= 𝜆 −𝑛−1 ( 𝑥 1 − 𝑥 0 ) tal que si existe un 𝑦∈ Λ 𝜖 con |𝑥−𝑦|<𝛿 entonces 𝑥,𝑦∈ 𝐼 ?? 0 … 𝑠 𝑛 ; es decir, 𝑆(𝑥) coincide con 𝑆(𝑦) en los primeros 𝑛+1 términos de la sucesión. En consecuencia, 𝑑(𝑆(𝑥),𝑆(𝑦))≤ 1 2 𝑛 <𝜀′.
Continuidad de la inversa. La inversa de la función itinerario esta definida como: 𝑆 −1 : 𝛴 2 ⟼ Λ 𝜖 , donde 𝑆 −1 ( 𝑠 0 … 𝑠 𝑛 …)=𝑥.
Dado 𝜀′>0, por el lema 3.9 sabemos que existe 𝑛∈ℕ tal que 𝜆 −𝑛−1 ( 𝑥 1 − 𝑥 0 )<𝜀′. Sean 𝑠,𝑡∈ 𝛴 2 tales que 𝑑(𝑠,𝑡)< 1 2 𝑛 entonces, se cumple que 𝑠 𝑗 = 𝑡 𝑗 para todo 𝑗=0:𝑛. Por lo tanto 𝑆 −1 (𝑠), 𝑆 −1 (𝑡)∈ 𝐼 𝑠 0 … 𝑠 𝑛 , es decir que tomando 𝛿= 1 2 𝑛 se tiene que | 𝑆 −1 (𝑠)− 𝑆 −1 (𝑡)|≤ 𝜆 −𝑛−1 ( 𝑥 1 − 𝑥 0 )<𝜀′, así, se concluye que 𝑆 −1 es continua.
Nos falta probar que, 𝑆∘ 𝐵 𝜖 (𝑥)=𝜎∘𝑆(𝑥), para todo 𝑥∈ Λ 𝜖 . Para ello, sea 𝑥∈ Λ 𝜖 , luego sabemos que existe una única intersección de intervalos encajados tal que 𝑥= ∩ 𝑛≥0 𝐼 𝑠 0 … 𝑠 𝑛 … , determinada por el itinerario de 𝑆(𝑥)=𝑠=( 𝑠 0 𝑠 1 …), como 𝐼 𝑠 0 … 𝑠 𝑛 = 𝐼 𝑠 0 ∩ 𝐵 𝜖 −1 ( 𝐼 𝑠 1 )∩…∩ 𝐵 𝜖 −𝑛 ( 𝐼 𝑠 𝑛 ), por el lema 3.8 sabemos que 𝐵 𝜖 ( 𝐼 𝑠 0 … 𝑠 𝑛 )= 𝐼 𝑠 1 … 𝑠 𝑛 . Por lo tanto 𝐵 𝜖 𝑥 ∈ ∩ 𝑛≥1 𝐼 𝑠 1 … 𝑠 𝑛 ; en consecuencia, (ecuación 12, 13 ,14 y 15)
Corolario 3.11 Sea 𝐵 una transformación tipo Boole. Si 𝜖 1 >0 y 𝜖 2 >0, entonces 𝐵 𝜖 1 | 𝛬 𝜖 1 y 𝐵 𝜖 2 | 𝛬 𝜖 2 son topológicamente conjugados.
Proof. Sean 𝜖 1 >0 y 𝜖 2 >0 arbitrarios, por el Teorema 1, se concluye que tanto 𝐵 𝜖 1 como 𝐵 𝜖 2 son topológicamente conjugados con 𝜎, donde la aplicación itinerario es la conjugación topológica para dichas funciones. Por transitividad, se sigue que 𝐵 𝜖 1 | Λ 𝜖 1 ∼ 𝐵 𝜖 2 | Λ 𝜖 2 .
Como consecuencia de la demostración obtenemos que
Teorema 3.12 Sea 𝑓:ℝ\{0}⟶ℝ de clase 𝐶 1 tal que 𝑓′(𝑥)>0 para todo 𝑥≠1. Si existen intervalos 𝐽 0 =[ 𝑎 0 , 𝑏 0 ]⊂(−∞, 0) y 𝐽 1 =[ 𝑎 1 , 𝑏 1 ]⊂(0, +∞) tales que 𝑓′(𝑥)>1 para todo 𝑥∈ 𝐽 0 ∪ 𝐽 1 y 𝑓( 𝐽 0 )=[ 𝑎 0 , 𝑏 1 ]=𝑓( 𝐽 1 ), entonces
Λ 𝑓 = ∩ 𝑛≥1 𝑓 −𝑛 ( 𝐽 0 ∪ 𝐽 1 ) es un conjunto de cantor invariante por 𝑓;
𝑓 | Λ 𝑓 es transitivo y el conjunto de puntos periódicos es denso;
𝑓 | Λ 𝑓 es topológicamente conjugado al shift unilateral 𝜎: 𝛴 2 → 𝛴 2 .
3.3 Demostración del Teorema Principal
Recordemos que (ecuación 16)
para 𝑖=0, 1, 2. Decimos que 𝑔 ∈ 0 es 𝛿− 𝐶 0 próximo de 𝐵 𝜖 si |𝑔(𝑥)− 𝐵 𝜖 (𝑥)|<𝛿 para todo 𝑥≠0. También, decimos que 𝑔 ∈ 1 es 𝛿− 𝐶 1 próximo de 𝐵 𝜖 si 𝑔 es 𝛿− 𝐶 0 próximo de 𝐵 𝜖 y |𝑔′(𝑥)− 𝐵′ 𝜖 (𝑥)|<𝛿 para todo 𝑥≠0.
Lema 3.13 Para cualquier 0< 𝛿 0 <1 y para toda función 𝑔 ∈ 0 tal que 𝑔 es 𝛿 0 − 𝐶 0 próximo de 𝐵 𝜖 , se cumple que:
lim 𝑥→+∞ 𝑔(𝑥)=+∞ y lim 𝑥→−∞ 𝑔(𝑥)=−∞.
lim 𝑥→ 0 + 𝑔(𝑥)=−∞ y lim 𝑥→ 0 − 𝑔(𝑥)=+∞
Proof. Por hipótesis tenemos que:
|𝑔(𝑥)− 𝐵 𝜖 (𝑥)|< 𝛿 0 , 𝑝𝑎𝑟𝑎 𝑡𝑜𝑑𝑜 𝑥∈ℝ\{0}
⇐− 𝛿 0 <𝑔(𝑥)− 𝐵 𝜖 (𝑥)< 𝛿 0
⇐ 𝐵 𝜖 𝑥 − 𝛿 0 <𝑔 𝑥 < 𝐵 𝜖 𝑥 + 𝛿 0 ,
Luego, aplicando los límites correspondientes obtenemos el resultado.
El siguiente resultado es bien conocido, la diferencia aquí es que precisamos el intervalo donde aparece el nuevo punto fijo de la transformación perturbada.
Observación 3.14 Si 𝐵 una transformación tipo Boole y 𝜖>0, entonces dado 𝑀>0 existe 𝜆>1 tal que 𝐵 𝜖 ′(𝑥)>𝜆 para todo 𝑥∈[−𝑀, 0)∪(0, 𝑀].
Lema 3.15 Si 𝐵 una transformación tipo Boole y 𝜖>0, entonces existe 𝛿 2 > tal que si 𝑔 es 𝛿 2 − 𝐶 1 próximo de 𝐵 𝜖 se tiene:
existe un único 𝑝 + ∈(0, +∞) tal que 𝑔( 𝑝 + )= 𝑝 + ;
existe un único 𝑝 − ∈(−∞, 0) tal que 𝑔( 𝑝 − )= 𝑝 − ;
existe 𝜆>1 tal que 𝑔′(𝑥)>𝜆 para todo 𝑥∈[ 𝑝 − , 0)∪(0, 𝑝 + ].
Proof. Como 𝐵 𝜖 (𝑥)−𝑥⟶𝜖 cuando 𝑥→+∞ y también 𝐵 𝜖 (𝑥)−𝑥⟶−𝜖 cuando 𝑥→−∞, existe 𝑀> 𝑚𝑎𝑥 { 𝑥 1 , − 𝑥 0 } tal que | 𝐵 𝜖 (𝑥)−𝑥|> 𝜖 2 , para todo |𝑥|≥𝑀. Luego, por la observación 3.14 existe 𝜆 1 >1 tal que 𝐵 𝜖 ′(𝑥)> 𝜆 1 para todo 𝑥∈[−𝑀, 0)∪(0, 𝑀]. Ahora, por otro lado, considere 𝛿>0, pero acotado superiormente de la siguiente forma: 𝛿< min − 1 4 𝑥 0 , 1 4 𝑥 1 , 1 4 𝑀− 𝑥 1 , 1 4 𝑥 0 +𝑀 . También, considere 𝛿 1 >0 suficientemente pequeño tal que 𝛿 1 < 1 2 min 𝐵 𝜖 𝑥 1 −𝛿 − 𝑥 1 −𝛿 , 𝐵 𝜖 𝑥 1 +𝛿 − 𝑥 1 +𝛿 , 𝜖 2 , 𝜆 1 −1 . Para este 𝛿 1 , considere 𝑔 𝛿 1 − 𝐶 1 próximo de 𝐵 𝜖 . Entonces, (ecuación 17), (ecuación 18)
Como, 𝛿+ 𝐵 𝜖 ( 𝑥 1 −𝛿)−( 𝑥 1 −𝛿)< 𝛿 2 −2 𝛿 2 <0 se sigue que, 𝑔( 𝑥 1 −𝛿)−( 𝑥 1 −𝛿)<0, es decir, 𝑔( 𝑥 1 −𝛿)<( 𝑥 1 −𝛿). Ahora, de la forma en que fue tomado 𝛿 2 se tiene que − 𝛿 2 + 𝐵 𝜖 ( 𝑥 1 +𝛿)−( 𝑥 1 +𝛿)>− 𝛿 2 +2 𝛿 2 >0, por tanto 𝑔( 𝑥 1 +𝛿)>( 𝑥 1 +𝛿). Por el Teorema de valores intermedios existe ?? + ∈( 𝑥 1 −𝛿, 𝑥 1 +𝛿). Por otro lado, ya que 𝑔 es 𝛿 1 − 𝐶 1 próximo de 𝐵 𝜖 . Entonces, − 𝛿 2 + 𝐵 𝜖 ′(𝑥)<𝑔′(𝑥)< 𝛿 2 + 𝐵 𝜖 ′(𝑥) para todo 𝑥∈ℝ\{0}. Ya que, 𝛿 2 se tiene que − 𝛿 2 + 𝐵 𝜖 ′(𝑥)>− 𝛿 2 + 𝜆 1 para todo 𝑥∈(0, 𝑀] y de la forma en que tomamos 𝛿 2 , tenemos − 𝛿 2 + 𝐵 𝜖 ′(𝑥)>− 1 2 ( 𝜆 1 −1)+ 𝜆 1 =1+ 1 2 𝜆 1 . De esto, tomando 𝜆:=1+ 1 2 𝜆 1 , resulta que 𝑔′(𝑥)>𝜆 para todo 𝑥∈(0, 𝑀]. Esto junto con el hecho que 𝑝 + ∈(0, 𝑀] prueba el item c) y prueba que 𝑝 + es el único punto fijo en (0, 𝑀]. Sea 𝑥>𝑀, entonces 𝐵 𝜖 (𝑥)−𝑥> 𝜖 2 . Como − 𝛿 2 + 𝐵 𝜖 (𝑥)<𝑔(𝑥) y de la escogencia de 𝛿 2 , (ecuación 19)
Luego, 𝑔(𝑥)>𝑥. Con esto probamos el item a). La prueba del item b) es análoga y se toma al final el menor 𝛿 2 .
Proof. Teorema Principal 1
Sea 𝜖>0, considere 𝛿 2 >0 como en el lema 3.15. Considere 𝑔 ∈ 1 tal que 𝑔 es 𝛿 2 − 𝐶 1 próximo de 𝐵 𝜖 . Entonces, 0<1− 𝛿 2 <{𝑔′(𝑥):𝑥∈ℝ\{0}} lo que implica que 𝑔 es monótona creciente restringida sobre cada componente conexa, en consecuencia 𝑔 | (−∞,0) :(−∞,0)↦ℝ y 𝑔 | (0,+∞) :(0,+∞)↦ℝ son homeomorfismos. Denotemos los puntos fijos de 𝑔 como 𝑦 0 := 𝑝 − y 𝑦 1 ;= 𝑝 + . También, denotaremos por 𝑦 10 a la preimagen positiva de 𝑦 0 y 𝑦 01 a la preimagen negativa de 𝑦 1 , esto es 𝑔 + −1 ( 𝑦 0 )= 𝑦 10 y 𝑔 − −1 ( 𝑦 1 )= 𝑦 01 . Definimos 𝐽 0 :=[ 𝑦 0 , 𝑦 01 ]⊂(−∞,0) y 𝐽 1 :=[ 𝑦 10 , 𝑦 1 ]⊂(0,+∞). Entonces, por el lema 3.15 𝑔′(𝑥)>1 para todo ??∈ 𝐽 0 ∪ 𝐽 1 . En consecuencia, aplicando el Teorema 3.12 (ecuación 20)
es un conjunto de cantor, Λ 𝑔 es transitivo respecto 𝑔 | Λ 𝑔 y 𝑔 | Λ 𝑔 es topológicamente conjugado al shift unilateral 𝜎: 𝛴 2 → 𝛴 2 . Por el Teorema 1.2, 𝐵 𝜖 | Λ 𝐵 𝜖 es topológicamente conjugado al shift unilateral 𝜎: 𝛴 2 → 𝛴 2 . Por transitividad de la conjugación topológica 𝑔 | Λ 𝑔 es topológicamente conjugado a 𝐵 𝜖 | Λ 𝐵 𝜖 . En consecuencia, 𝐵 𝜖 es robustamente transitivo.
Corolario 3.16 Sea 𝑔 ∈ 1 tal que 𝑔 es 𝛿 2 − 𝐶 1 próximo de 𝐵 𝜖 . Si 𝑥∈ 𝛬 𝑔 𝑐 \( ∪ 𝑛≥0 𝑔 −𝑛 (0)), entonces | 𝑔 𝑛 (𝑥)|→+∞, cuando 𝑛→+∞.
La prueba es análoga a la proposición 3.5, aplicando el lema 3.15
3.4 Ejemplos de Aplicación
Considere la transformación 𝐵 𝑎 :ℝ\{0}⟶ℝ definida por 𝐵 𝑎 (𝑥)=𝑥− 𝑎 𝑥 . Note que, 𝐵 𝑎′ (𝑥)>1 para todo 𝑥≠0, 𝐵 𝑎 tiene asíntota vertical en 𝑥=0 y la recta 𝑦=𝑥 es una asíntota oblicua. 𝐵 𝑎 no tiene puntos fijos, de hecho, 𝐵 ( 𝑥)<𝑥 si 𝑥>0 y 𝐵 𝑎 (𝑥)<𝑥 si 𝑥<0. Lo que significa que 𝐵 𝑎 es una transformación tipo Boole para toda 𝑎>0. Aplicando el Teorema Principal a la transformación. (ecuación 21)
tenemos que 𝐵 𝑎𝜖 es robustamente transitiva para todo 𝑎>0 y 𝜖>0. Esto es, existe un conjunto de cantor Λ 𝑎𝜖 invariante tal que 𝐵 𝑎𝜖 restricto a Λ 𝑎𝜖 es transitiva. Además el conjunto de puntos periódicos es denso en Λ 𝑎𝜖 .
4 Conclusión
a) Si consideramos 𝐵(𝑥)=𝑥− 1 𝑥 la famosa transformación de Boole. Entonces su traslación 𝐵 𝜖 converge uniformemente a 𝐵, cuando 𝜖→0. Observe que, 𝐵 está siendo aproximada por transformaciones robustamente tansitivas. Note que, para cada 𝜖>0, Λ 𝜖 ⊂ − 1 𝜖 , 1 𝜖 , donde − 1 𝜖 , 1 𝜖 es el intervalo compacto más pequeño que contiene a Λ 𝜖 . En [Muñoz, 2015] se prueba para 𝐵 y las transformaciones tipo Boole que Λ 𝐵 =ℝ\ ∪ 𝑛≥0 𝐵 −𝑛 (0) es un conjunto residual, totalmente disconexo, invariante y transitivo. Contrastando ésto con nuestro resultado, nos hacemos las siguientes preguntas:
Pregunta 4.1 Si 𝐵 es una transformación tipo Boole. De qué forma converge 𝛬 ? a 𝛬 𝐵 , cuando 𝜖→0.
Pregunta 4.2 A patir de qué valor de 𝜖>0 se obtiene que la medida de Lebesgue de 𝛬 𝜖 es positiva.
Pregunta 4.3 Si 𝐵 es una transformación tipo Boole. 𝐵 𝜖 posee una medida invariante absolutamente continua a la de Lebesgue. Tal medida es ergódica.
b) De la forma en que se abordó la demostración del Teorema 1.2, si 𝑔 ∈ 1 es una perturbación 𝐶 1 de una transformación tipo Boole, tal que 𝑔 tiene un único punto fijo en cada componente conexa, digamos 𝑦 0 <0 y 𝑦 1 >0, y 𝑔 satisface que 𝑔′(𝑥)>1 para todo 𝑥∈[ 𝑦 0 , 𝑦 1 ]. Enotnces, existe un conjunto de cantor Λ 𝑔 invariante tal que 𝑔 restricto a Λ 𝑔 es transitivo. Haciendo el mismo tipo de perturbación que se hizo para la demostración del Teorema Principal se puede mostrar que 𝑔 es robustamente transitiva.
Para probar que Λ 𝑔 es transitivo, se hace consiguiendo una conjugación topológica entre 𝑔 | Λ 𝑔 el shift unilateral 𝜎: Σ 2 ⟶ Σ 2 . En consecuencia 𝑔 | Λ 𝑔 tiene la misma dinámica que las traslaciones de las transformaciones tipo Boole.
c) Sea 𝐵 una transformación tipo Boole. Consideremos 𝜖>0 y definamos la traslación. (ecuación 22)
Note que, 𝐵 𝜖 no posee puntos fijos, pero sigue teniendo asíntota vertical en 𝑥=0 y 𝐵 𝜖 ′(𝑥)>1 para todo 𝑥≠0. En Muñoz (2015) se prueba que Λ 𝐵 𝜖 =ℝ\ ∪ 𝑛≥0 𝐵 𝜖 −𝑛 (0) es un conjunto residual, totalmente disconexo invariante y transitivo respecto a 𝐵 𝜖 . Entonces
Pregunta 4.4 La transformación 𝐵 𝜖 es robustamente transitiva.
d) Considere la familia a dos parámetros 𝐵 𝑎𝜖 de la subsección 3.4, aplicando el Teorema Principal y el corolario 3.11, se tiene que si los parámetros 𝑎, 𝑎′, 𝜖, 𝜖′>0, entones 𝐵 𝑎𝜖 | Λ 𝑎𝜖 es topológicamente conjugado a 𝐵 𝑎′𝜖′ | Λ 𝑎′𝜖′ .
e) Considere la familia a dos parámetros de la transformación de Boole, 𝐵 𝑎𝜖 (𝑥)=𝑥− 𝑎 𝑥 +𝜖, para 𝑎>0 y 𝜖>0, estudiada en Prykarpatsky & Feldman (2006).
Pregunta 4.5 La transformación de Boole, posee un conjunto invariante totalmente disconexo, no cerrado, no acotado y robustamente transitivo.