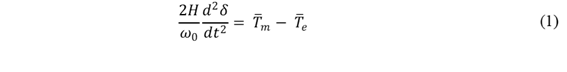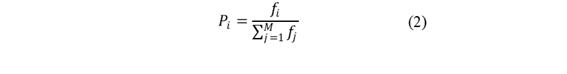INTRODUCCIÓN
Históricamente, la evaluación de la estabilidad transitoria de un Sistema Eléctrico de Potencia (SEP) se ha llevado a cabo fuera de línea, dado el tiempo de cómputo necesario para determinar por simulación la respuesta dinámica sobre el modelo del SEP. La evaluación de la estabilidad transitoria mediante estos métodos de integración paso a paso, que resuelven las ecuaciones diferenciales y que representan la dinámica del sistema, son capaces de manejar grandes sistemas de potencia con gran cantidad de generadores, teniendo en cuenta modelos validados de los elementos presentes en un sistema eléctrico de potencia real [1], [2].
Si bien esta metodología es muy útil en la fase de planificación, los estudios para el ajuste de un esquema de desconexión automática de generación (DAG) no pueden considerar un gran número de estados de operación y contingencias al estar limitados por el componente humano. Adicionalmente, los métodos de integración paso a paso son computacionalmente exigentes, y dada la rápida naturaleza del fenómeno de inestabilidad transitoria, hacen que sea imposible su implementación en tiempo real.
Por otro lado, existen métodos directos cuya finalidad es obtener información sobre el estado de la estabilidad transitoria sin realizar simulaciones, lo que optimiza los tiempos para que puedan ser aplicados en tiempo real [1],[3]. No obstante, la principal limitación de estos métodos radica en la complejidad de gestionar modelos de las máquinas y otros componentes del sistema; por ejemplo, en el método Equivalente de Máquina Simple-Barra Infinita, se reduce al sistema completo en un equivalente donde se pueda aplicar la metodología de igualdad de áreas para determinar un margen de estabilidad.
En contraste a lo anterior, las unidades de medición sincrofasorial ofrecen una visión completa de la dinámica del sistema eléctrico. Además, su frecuencia de muestreo abre las puertas a nuevas oportunidades para generar metodologías que puedan, en tiempo real, evaluar el estado de la estabilidad y decidir acciones de control correctivo para mitigar fenómenos inestables transitorios.
Como antecedente al presente trabajo, se puede mencionar a la investigación [4], donde al utilizar máquinas de aprendizaje y mediciones de PMUs se construye una metodología para catalogar el estado de estabilidad de corto plazo para clasificar estados estables, inestable transitorio e inestable por pérdida de la estabilidad de tensión a corto plazo (STVS), dado que ambos tipos de inestabilidades se desarrollan en la misma ventana de tiempo. En este sentido, el presente trabajo aprovecha este desarrollo para hacer frente a problemas de inestabilidad transitoria, y se proponen acciones de control de emergencia correspondiente a la desconexión de plantas de generación.
En este sentido, con una discriminación del estado de estabilidad a corto plazo proporcionado por [4], la presente investigación tiene como objetivo identificar generadores críticos para construir un Esquema de Desconexión Automática de Generación (EADG).
Este trabajo consta de 5 capítulos que detallan el proceso de identificación de generadores críticos; el capítulo 2 explora conceptos clave para entender la metodología, además de presentar las herramientas tecnológicas y matemáticas necesarias para el desarrollo de la misma. El capítulo 3 detalla la metodología propuesta y el capítulo 4 evidencia los resultados de su aplicación en un ambiente de simulación. Finalmente, el capítulo 5 destaca las conclusiones más importantes del trabajo.
Marco teórico
Para contextualizar la investigación, en el presente capítulo se presenta el marco teórico sobre la estabilidad transitoria de los sistemas de potencia y las herramientas necesarias para aplicar la metodología propuesta.
Estabilidad transitoria
La estabilidad de un SEP se define como su capacidad para volver a un estado de equilibrio operativo después de haber sido afectado por una perturbación, partiendo de una condición inicial específica [5].
Particularmente, la estabilidad transitoria se define como la capacidad de un SEP para mantener a los generadores en sincronismo y lograr condiciones de funcionamiento aceptables en estado estacionario tras enfrentar grandes perturbaciones, como cortocircuitos, la pérdida de grandes unidades de generación o importantes variaciones en la carga [5]. La variable que mejor representa fenómenos donde la estabilidad transitoria está involucrada, es el ángulo de rotor de la maquina; la ecuación (1) describe las oscilaciones de este ángulo durante perturbaciones.
Donde, T m representa el torque mecánico proporcionado por la fuerza motriz que actúa en el eje de la máquina y 𝑇 𝑒 el torque electromagnético generado por la reacción de la armadura; 𝐻 es la constante de inercia de la máquina; 𝜔 0 es la velocidad angular nominal en rad/s; y 𝛿 corresponde a la posición angular del rotor con respecto a un marco de referencia síncrono.
Sistemas especiales de protección
Los sistemas especiales de protección (SPS) realizan acciones de control predefinidas post contingencia y son estructurados a partir de simulaciones fuera de línea donde se evalúa la seguridad estática y dinámica del sistema [1]; los sistemas especiales de protección suelen caracterizarse por [6]:
• Actuar en contingencias poco comunes, que suelen estar fuera del rango de diseño destinado a soportar una potencia firme, lo que permite realizar acciones de control que no se utilizan en condiciones operativas normales, como la reducción de carga y generación.
• Asumir mayores riesgos operacionales, con consecuencias que podrían superar la capacidad de protección convencional.
• Realizar protección a nivel de sistema, que funciona en varias ubicaciones y coordina el control de múltiples señales de manera integrada.
Según sus variables de control, los SPS se pueden clasificar en dos tipos: basados en respuesta y basados en eventos. Por una parte, los SPS basados en eventos están diseñados para actuar al identificar una contingencia o una combinación específica de eventos como pérdidas de varias líneas de transmisión o varios generadores. Estos SPS basados en eventos son más rápidos porque no necesitan esperar la reacción del sistema ante un evento particular, sin embargo, necesitan que se evalúen muchos escenarios para definir su operación [6].
Por otra parte, los SPS basados en respuesta se activan según las variables eléctricas medidas cómo tensión o frecuencia y llevan a cabo acciones protectoras cuando el valor medido alcanza un nivel de umbral tras una contingencia; de este modo, son capaces de manejar situaciones no planificadas [6].
El Esquema Adaptable de Desconexión de Generación (EADG) propuesto se asemeja a un SPS basado en eventos ya que, al usar mecanismos de inteligencia artificial, en su entrenamiento está considerando distintos escenarios de operación y contingencias, con la diferencia de que toma en cuenta una enorme cantidad de los mismos (en contraste a un SPS convencional). Del mismo modo, el EADG se asemeja a un SPS basado en la respuesta ya que, para tomar la decisión de activación y definición de parámetros, es necesario contar con mediciones que evidencien la dinámica del sistema.
METODOLOGÍA
La metodología propuesta tiene como objetivo identificar la generación crítica que causa inestabilidad en situaciones de pérdida de estabilidad transitoria. Esta identificación se utilizará para etiquetar los generadores en la base de datos, que servirá como insumo fundamental para entrenar un modelo de inteligencia artificial (IA) supervisado. Este modelo, basado en mediciones de PMU de tensión compleja en las terminales y en la estimación del ángulo del rotor de las máquinas síncronas, clasificará a los generadores como críticos o no críticos, lo que permitirá parametrizar en tiempo real el EADG.
3.1. Generación de la base de datos
La creación de la base de datos es crucial en el desarrollo de cualquier metodología que utilice herramientas de inteligencia artificial, en este sentido, los datos deben ser suficientes y variados para abarcar una amplia gama de escenarios de operación y fallas del sistema.
3.1.1 Escenarios de operación
La herramienta para construir el conjunto de escenarios de operación es la simulación de Monte Carlo, simulación que debe representar el comportamiento de la red lo más fielmente posible. Por tanto, se emplean modelos probabilísticos de variables aleatorias del sistema de potencia, que consideran un horizonte de análisis a corto plazo (5s) dado que los fenómenos inestables transitorios se dan en este intervalo temporal [7] [8] [9].
Para la generación de la base de datos este trabajo considera como horizonte de interés al de 24 horas. El modelo de pronóstico de carga debe reflejar adecuadamente el comportamiento de la carga del sistema y sus incertidumbres asociadas, utilizando funciones de distribución de probabilidad (PDF) apropiadas. Estas incertidumbres se consideran a través de distribuciones normales, que se incorporan en las simulaciones de contingencias basadas en Montecarlo. En el sistema de prueba, se adaptaron tres curvas de carga típicas para clientes residenciales, comerciales e industriales.
El pronóstico siempre tendrá un grado de incertidumbre respecto al comportamiento real de la carga, lo que implica que se deben incluir distribuciones normales en la formación de las cargas nodales por hora. Por otro lado, la planificación operativa a corto plazo para satisfacer la demanda pronosticada en las próximas 24 horas, conocida como "Unit-commitment", implica optimizar el cronograma de generación, sujeto a restricciones específicas. En este trabajo, se asume que esta optimización ya ha sido realizada y se dispone de un cronograma de unidades de generación, incluyendo la reserva rodante, que será utilizado en el análisis posterior.
La planificación operativa también aborda la determinación de la topología de la red, considerando los activos de transmisión disponibles y sus mantenimientos. El objetivo es optimizar la flexibilidad y eficiencia de la red en función de la demanda y el cronograma de generación previamente definido. En este trabajo, se asume que la topología de la red a corto plazo ha sido determinada por el operador y se utilizará como entrada para la metodología propuesta, enfocada en resolver un Flujo Óptimo de Potencia (OPF) hora a hora.
3.1.2 Simulación de contingencias N-1
En este estudio se asume que las contingencias N-1 son eventos independientes generados de manera aleatoria, que incluyen la pérdida de plantas de generación y cortocircuitos trifásicos en líneas de transmisión. Las contingencias seleccionadas están adaptadas al sistema bajo estudio, centrándose en las perturbaciones más probables y aquellas que generan el mayor estrés. La probabilidad de cada tipo de falla se deriva de datos históricos y sigue una distribución de probabilidad discreta y se calcula por medio de la ecuación (2).
Donde 𝑃 𝑖 , es la probabilidad de falla i-ésima, 𝑓 𝑖 es el número de veces que esta falla ocurre y M el número de tipos de fallas analizadas.
Además, la ubicación de la falla para las contingencias de cortocircuito se determina utilizando funciones de densidad de probabilidad adecuadas y basadas en estadísticas históricas. La generación aleatoria de contingencias utiliza funciones de distribución tanto uniforme como de Weibull [10]. Así, una vez definidas las distribuciones de probabilidad adecuadas, es necesario elegir un método de muestreo para extraer las muestras aleatorias de contingencia conforme a sus distribuciones. Según el análisis realizado en [8] y [9], se opta por la técnica de muestreo aleatorio para la simulación de Monte Carlo, ya que ha mostrado ofrecer mejores resultados en cuanto a la media y la varianza en el análisis probabilístico de la dinámica del sistema eléctrico.
3.1.3 Series de tiempo de simulaciones dinámicas
La finalidad de construir una base de datos de escenarios operativos y de contingencias N-1 es para utilizarlas en la obtención de series de tiempo de variables del sistema eléctrico que ofrezcan una visión adecuada de la estabilidad transitoria del sistema.
Estas series de tiempo deben ser seleccionadas con el fin de permitir la identificación precisa de plantas generadoras críticas en una ventana de tiempo reducida. Es decir, las variables elegidas deben reflejar de manera efectiva los problemas de estabilidad transitoria. Además, estas variables deben ser medidas o estimadas con dispositivos PMU, para que la metodología pueda ser usada en tiempo real.
Diferentes estudios como [11] y [12] sugieren que el ángulo de la tensión puede reflejar el estado de las máquinas síncronas del sistema, sin embargo, dado que con algunos tipos de PMU se puede acceder también a mediciones del módulo de la tensión en barras de generación y a el mismo ángulo del rotor de la máquina con algunos tipos de PMU [13], hace que se escoja a estas tres variables (Ө, U, δ) para entrenar con series de tiempo de las mismas, un modelo de inteligencia artificial. En tiempo real, el monitoreo de estas tres variables eléctricas del sistema de potencia proporcionará la información para la parametrización y activación del EADG.
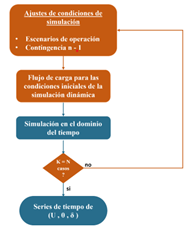
La Fig. 1 muestra el proceso para obtener las series de tiempo mencionadas bajo los diferentes escenarios de operación y falla, donde k es el número del caso simulado y n el número total de casos para construir la base de datos.
3.1.4 Identificación de generadores críticos
Con el fin de generar el etiquetado de generadores críticos, para usarlo en el entrenamiento de un modelo de IA, es necesario encontrar las plantas de generación causantes de la inestabilidad en el sistema para cada uno de los casos inestables por pérdida de la estabilidad transitoria.
Dado que la variable que mejor representa la estabilidad
transitoria es el ángulo del rotor de la máquina, se escoge esta variable para encontrar las máquinas que alcanzan la inestabilidad en cada escenario clasificado como inestable por estabilidad transitoria.
En este sentido, se crea un ranking de desconexión según el orden en que cada máquina alcanza el límite de estabilidad transitoria para cada caso. Este resultado se usará para encontrar mediante simulaciones dinámicas las plantas que, al ser desconectadas, permiten que el sistema mantenga la estabilidad transitoria. A continuación, se describe esta metodología a detalle.
Ranking de desconexión:
El primer paso para encontrar los generadores críticos es crear un ranking de desconexión, basado en el tiempo en el que el ángulo del rotor de cada máquina alcanza el límite teórico de estabilidad (180° o -180°) [14].
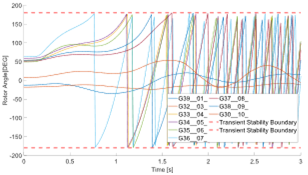
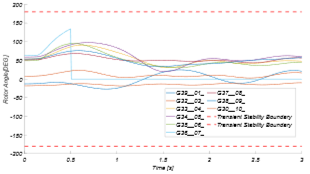
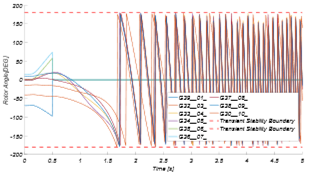
Con el fin de entender mejor el proceso, se ejemplifica cómo se construye el ranking para el caso inestable de la Fig. 2. En este caso, la pérdida de la estabilidad transitoria es ocasionada por una falla trifásica en la línea L22-L23 del sistema IEEE New England de 39 barras en un estado de operación con alta carga. La respuesta a esta perturbación de los ángulos del rotor de las máquinas del sistema es obtenida mediante simulación dinámica en el programa DigSILENT Power Factory.
La Fig. 2 muestra los ángulos de los rotores de las máquinas en una ventana de 3 segundos; donde se puede apreciar la ocurrencia de la falla mencionada a los 100 ms de iniciada la simulación, y su despeje exitoso 100ms después. De acuerdo con la metodología planteada, el ranking de este caso se forma por 6 generadores en el orden que presenta la Tabla 1, donde G36 es el primero que alcanza el límite de 180º y G37 el último.
Etiquetado de generadores críticos:
Después de tener el insumo necesario para encontrar los generadores críticos (ranking de desconexión), se desarrolló un algoritmo que lleva a cabo simulaciones dinámicas, este desconecta los generadores de uno en uno de forma acumulativa, siguiendo el orden establecido por el ranking, hasta que el sistema alcanza un estado estable.
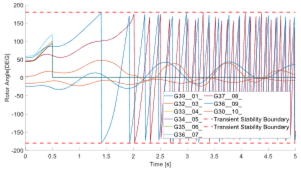
Retomando el caso mencionado anteriormente, para ejemplificar la metodología, la Fig. 3 muestra la simulación dinámica final, donde la inestabilidad ha sido mitigada al desconectar solo el primer generador del ranking, G36. De este modo, para este estado de operación/contingencia, el generador G36 será el único etiquetado como generador crítico, información necesaria para el entrenamiento del modelo de aprendizaje con que se implementaría el EADG.
Para este caso, la desconexión de todos los generadores que alcanzan el límite de estabilidad transitoria significaría la pérdida de alrededor del 60% de la capacidad de generación del parque, mientras que con la desconexión de los generadores críticos encontrados con la metodología precitada solo es necesario desconectar el 11 % de la capacidad de generación total para llevar al sistema a una condición estable.
Análisis de resultados
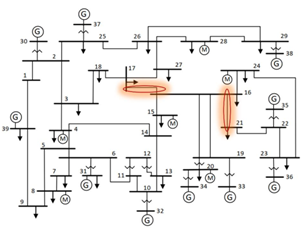
El sistema de prueba seleccionado para aplicar la metodología propuesta es el sistema IEEE New England de 39 barras de Nueva Inglaterra. Este sistema fue elegido sistema de prueba en varios estudios que abordan tareas similares, como la clasificación del estado de estabilidad de corto plazo [4] y la evaluación de márgenes de estabilidad transitoria [1], ambos emplean técnicas de aprendizaje automático como componente central. El sistema consta de 39 barras, 10 generadores que representan plantas de generación con generadores sincrónicos conectados en paralelo, 19 cargas y 46 líneas de transmisión que operan a un nivel de tensión de 345 kV y a una frecuencia de 60 Hz, Fig. 10.
Para representar de manera fiel los fenómenos transitorios propios de los estudios de estabilidad transitoria, se hace uso del modelo estándar del generador síncrono para simulaciones RMS (modelo subtransitorio de sexto orden) en el programa DigSilent PowerFactory [15]. De manera similar, y con el fin de considerar el fenómeno de la estabilidad de tensión a corto plazo (STVS), fenómeno que se presenta en la misma ventana de tiempo que la estabilidad transitoria, se considera un modelo dinámico de la carga presentado en [16].
La base de datos cuenta con 10000 casos de estudio, donde se contemplan diferentes estados de operación en conjunto con contingencias de fallas trifásicas y pérdida de generadores. Estos casos fueron clasificados en 3 categorías: 8407 estables, 1178 inestables por pérdida de estabilidad transitoria y 415 inestables por pérdida de estabilidad de tensión a corto plazo. La metodología para la clasificación del estado de estabilidad a corto plazo se puede consultar en [4].
El primer paso para encontrar los generadores críticos es utilizar la metodología de la sección 3.1.4 basada en el ranking de desconexión. Este ranking permite la desconexión uno a uno de estos generadores hasta que el sistema permanezca estable en una ventana de cinco segundos.
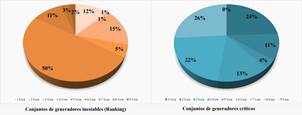
A continuación, en la Fig. 4 se muestra la cantidad de casos tanto de generadores que alcanzan el límite de estabilidad catalogados en el ranking, como los generadores críticos encontrados al aplicar la metodología propuesta, conjunto que al ser desconectado mitiga los problemas de estabilidad transitoria. Es decir, por ejemplo, para el caso del conjunto de 6 generadores se tiene que según el ranking corresponde a 562 casos, mientras que en realidad luego de la aplicación de la metodología se encuentra que en solo 295 casos se tiene un conjunto de 6 generadores críticos. Por otro lado, se tiene que en 62 de los casos inestable el ranking incluye 8 o 9 generadores mientras que no existen casos inestables donde se necesite de tal cantidad de generadores críticos para evitar la inestabilidad transitoria.
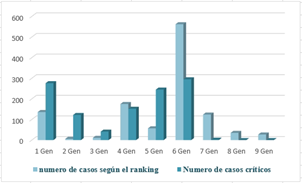
Figura 4: Cantidad de casos vs cantidad de generadores en el conjunto de generadores del ranking o en el conjunto de generadores críticos.
Por otra parte, se muestran en la Fig. 5 la distribución de porcentajes de los conjuntos de máquinas tanto para los generadores inestables (ranking) como para los generadores críticos. Como se puede apreciar en la Fig. 5, en el 50% de los casos se presenta 6 plantas inestables que con su desconexión el sistema se estabilizaría. Sin embargo, posterior a la aplicación de la metodología propuesta, solamente el 22% de los casos se identifica con 6 plantas críticas y que con su desconexión el sistema también puede estabilizarse. Del mismo modo se puede apreciar de que en aproximadamente un 5 % de los casos hay conjuntos de ocho y nueve plantas inestables, cuando en realidad en ningún caso es necesario disparar tantos generadores para lograr mitigar la inestabilidad. Otra situación extrema es el de los conjuntos formados por solo un generador, donde en el ranking se tiene alrededor del 12% de los casos en esta categoría, mientras que, gracias a la aplicación de la metodología propuesta, este porcentaje aumenta al 24 % de los casos.
Como resultado de este análisis, se logra identificar el número mínimo de generadores a ser desconectados con el fin de mitigar problemas de inestabilidad transitoria, evitando así, desconectar generación excesiva. Este resultado es un insumo clave para el entrenamiento de un modelo de IA núcleo del EADG a desarrollar en futuras investigaciones.
Del total de 1178 de casos inestables transitorios de la base de datos, la metodología fue capaz de etiquetar satisfactoriamente los generadores críticos en 1129 de ellos, es decir, se obtuvo una efectividad del 99.6 %.
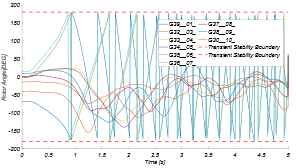
En los 4 casos con resultados no satisfactorios, la clasificación de generadores críticos por medio de la metodología propuesta resultó insuficiente. En estos casos, aunque la búsqueda de generadores críticos se realiza mediante la desconexión secuencial según el ranking, se observó que, al desconectar todos los generadores de este ranking (es decir, aquellos que alcanzaron el límite de estabilidad transitoria), algunos generadores que previamente no alcanzaban dicho límite comenzaron a hacerlo. Las Figs. 6 y 7 presentan las series de tiempo de los ángulos del rotor sin acciones de control, para dos de estos cuatro casos, con el fin de ilustrar este fenómeno.
Como se puede apreciar en las Figs. 6 y 7, en principio los casos no parecen demasiado críticos al observarse solo tres y cuatro generadores como inestables, respectivamente. Estas figuras muestran las incursiones de los ángulos del rotor de cada generador desde un estado estacionario, durante la falla (0.1 - 0.2 s) y luego su despeje exitoso en una ventana de simulación de cinco segundos. Cabe resaltar también que, en los casos de las Figs. 6 y 7 no se ha realizado ninguna acción de control correctiva específica.
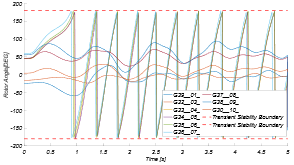
En las etiquetas bajo las series de tiempo de las Figs. 6 y 7 se puede encontrar el conjunto de generadores inestables, resultado de la aplicación de la metodología que construye el ranking de desconexión. Al proceder a desconectar uno a uno para encontrar el conjunto de generadores críticos se tiene que, aun cuando se desconectaron todos los generadores del ranking en cada uno de los casos, la inestabilidad no fue mitigada. Las Figs. 8 y 9 muestran la respuesta dinámica de los ángulos luego de la desconexión de los generadores del ranking.
Como se observa en las Figs. 8 y 9, después de desconectar todos los generadores del ranking, no fue posible mitigar la inestabilidad transitoria. En el caso 1, se puede notar que, tras la desconexión de las tres plantas inicialmente inestables, el resto de las máquinas también pierden sincronismo, lo que lleva a un colapso total del sistema. De manera similar, en el caso 2, aunque se desconectaron los generadores inestables según el ranking, no se logró evitar la inestabilidad, ya que los generadores G38 y G37, que previamente mantenían la estabilidad, pierden sincronismo después de aplicar la acción de control.
Si se analizan las condiciones del estado de operación previas a la falla, y las características de las mismas, se encuentra que estos cuatro casos se deben a fallas en las líneas L16-17 o L16-27, donde el cortocircuito ocurre en una localización cercana a las barras. Por otra parte, al considerar las condiciones prefalla, se puede evidenciar que el sistema de generación está operando cercano a sus máximos operativos, lo que representa una condición adversa en caso de una falla importante. Es decir, la confluencia de estas contingencias tan severas con los estados de operación extremos genera problemas en estos casos. En este sentido, estos estados operativos se deberían eludir para evitar incurrir en estos casos y no provocar situaciones muy inestables al presentarse fallas en las líneas mencionadas (Fig. 10).
CONCLUSIONES
Se ha definido una metodología para identificar generadores críticos cuya desconexión evita la inestabilidad transitoria. Esta metodología resulta indispensable para la obtención de una base de datos que sirva como insumo para construir un esquema adaptable de desconexión de generación (EADG) basado en modelos de IA.
La metodología propuesta fue evaluada en un entorno de simulación controlado utilizando el sistema de prueba de 39 barras de IEEE New England. Los resultados principales son los siguientes:
La metodología de identificación de la generación crítica ofrece una nueva perspectiva en el estudio de la estabilidad transitoria. Permite identificar y cuantificar la generación dinámica crítica discriminada en las plantas de generación necesarias para que, al ser desconectadas, se pueda mitigar la inestabilidad transitoria. Los resultados de la identificación fuera de línea mostraron una precisión del 99.65% en la identificación de generadores críticos, lo que proporciona una base sólida para su uso en el entrenamiento de máquinas inteligentes de clasificación y su posterior aplicación en tiempo real.
Si bien la metodología no tuvo resultados satisfactorios en el 100% de los casos, los 4 casos en que no logra identificar los generadores críticos son casos muy adversos que devienen de una combinación de condiciones de estrés alto al estar los generadores operando cerca de sus límites y de fallas severas. En este sentido, la recomendación es evitar estos casos operativamente. Un resultado similar se puede encontrar en [17].
Al obtener una base de datos sólida tanto de escenarios operativos y contingencias, así como de etiquetas de generadores críticos, se tiene el insumo necesario para construir un EADG cuyo núcleo son algoritmos de inteligencia artificial que puedan predecir conjuntos de generadores críticos considerando la respuesta dinámica del sistema ante una perturbación.
Este trabajo complementa el presentado en [4], con el objetivo de construir un esquema de desconexión de generación que aborde problemas de estabilidad transitoria, basándose en la clasificación previa del estado de estabilidad a corto plazo.