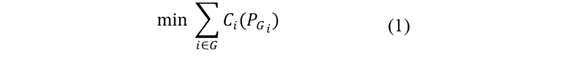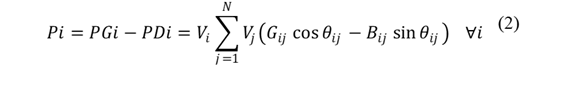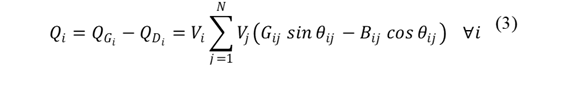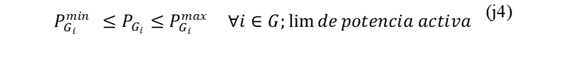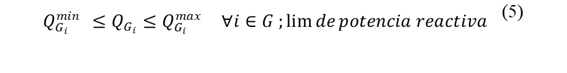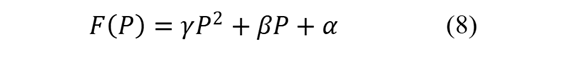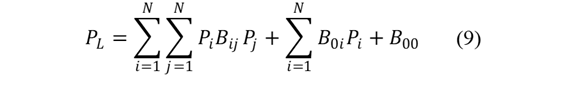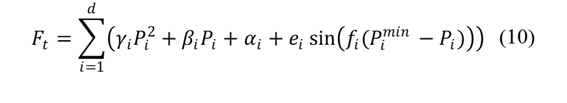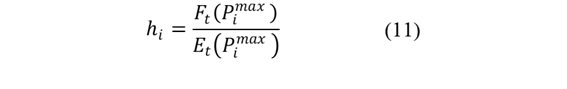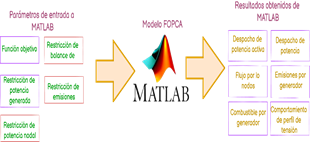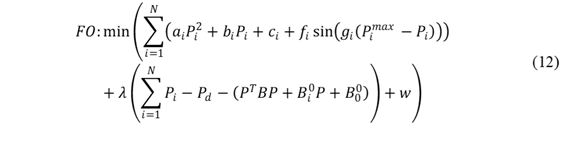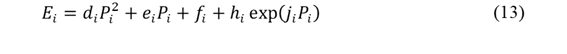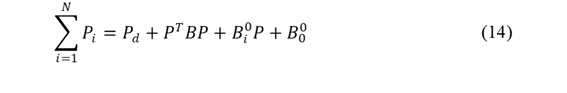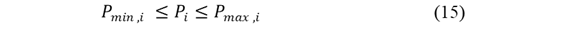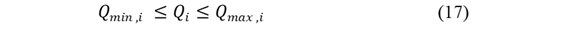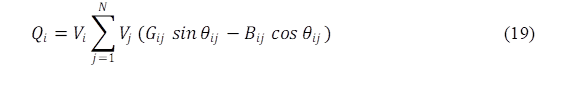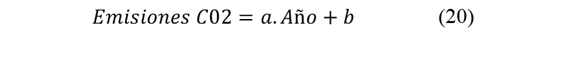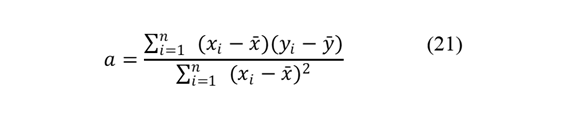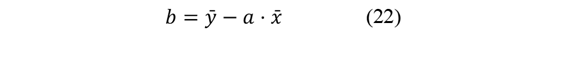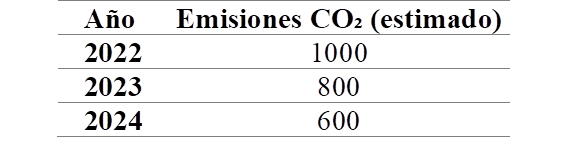INTRODUCCIÓN
Con el aumento de la preocupación global por el cambio climático y la urgente necesidad de crear sistemas energéticos sostenibles, la optimización de los flujos de potencia en los sistemas eléctricos, con consideraciones medioambientales, se ha vuelto esencial [1]. El campo de los Flujos Óptimos de Potencia con Consideraciones Ambientales (FOPCA) se enfoca en equilibrar eficiencia energética y sostenibilidad ambiental, integrando restricciones como las emisiones de gases contaminantes [2]. Este problema requiere reducir costos de producción, satisfacer la demanda de carga y cumplir restricciones operativas, al tiempo que se minimizan las emisiones de contaminantes como los óxidos de nitrógeno, azufre y dióxido de carbono [3] [4] [5]. Debido a su complejidad, este problema es multiobjetivo y no lineal, abordando simultáneamente costos operativos y emisiones ambientales [6] [7] [8].
Para su resolución, se han desarrollado múltiples métodos de optimización, desde técnicas clásicas, como los multiplicadores de Lagrange, hasta metaheurísticas más avanzadas [9]. Los métodos clásicos suelen proporcionar soluciones locales óptimas, pero las técnicas metaheurísticas, como la optimización por enjambre de partículas (PSO) y el algoritmo de la libélula (AL), son más efectivas para encontrar soluciones globales [10][11][12].
Diversos estudios han aplicado estas técnicas para resolver problemas de optimización en sistemas de energía, integrando fuentes como solar, eólica, hidroeléctrica y térmica [13]. Por ejemplo, se ha utilizado el algoritmo genético de clasificación no dominada II (NSGA-II) para minimizar costos de generación y emisiones, respetando las restricciones operativas [14]. De igual forma, el NSGA-II ha sido efectivo en sistemas eólicos y térmicos, optimizando simultáneamente costos y emisiones [15]. Además, la optimización por enjambre de partículas ha mostrado buenos resultados en sistemas que combinan plantas térmicas y solares [16].
Se han propuesto modelos más avanzados, como el despacho económico-ambiental, que consideran la respuesta a la demanda y el uso de tecnologías de control de contaminantes mediante programación lineal entera-mixta, lo que mejora la sostenibilidad operativa del sistema [17]. En un enfoque colaborativo, la optimización del despacho económico y de potencia reactiva en sistemas eléctricos ha mostrado ser efectiva en la reducción de costos y mejora de la estabilidad [18]. De manera similar, la combinación de plantas hidroeléctricas, eólicas y térmicas con el NSGA-II ha logrado un balance entre economía y sostenibilidad [19].
Otros estudios han desarrollado modelos de despacho económico con baja emisión de carbono para sistemas integrados de electricidad y gas, utilizando modelos de despacho estocástico de dos etapas [20]. También se ha optimizado el despacho económico-ambiental en sistemas híbridos térmicos y fotovoltaicos, empleando el método de optimización Ant Lion (ALO) para minimizar costos y emisiones [21]. Finalmente, se ha propuesto un algoritmo híbrido que combina el Algoritmo de Mercado de Intercambio (EMA) y la Optimización por Enjambre de Partículas con Peso Adaptativo (AIWPSO) para manejar problemas de optimización multiobjetivo, logrando reducir costos de generación y emisiones [22].
En los últimos años, diversos estudios amplían la comprensión de la optimización de flujos de potencia en sistemas eléctricos, abordando la optimización de la programación a través de flujo de emisión de carbono para control de intensidad de carbono, se ha logrado optimizar costos y emisiones [23], por otra parte, se ha rehalizado una revisión exahustiva sobre la gestión óptima de la energía combinada, reportando optimización en sistemas eléctricos con enfoque integral [24].
Este documento está estructurado de la siguiente manera: comienza con una introducción, seguida de una revisión del estado del arte en la optimización de flujos de potencia con consideraciones ambientales, destacando las contribuciones recientes en este campo. Posteriormente, se expone la metodología propuesta, incluyendo las herramientas y algoritmos utilizados para la optimización. A continuación, se presentan y discuten los resultados obtenidos, evaluando la eficacia de las estrategias implementadas y el impacto de las consideraciones ambientales en los sistemas de potencia eléctrica. Las conclusiones y recomendaciones del estudio se basan en los hallazgos analizados, proporcionando una visión crítica de las ventajas y limitaciones observadas.
MATERIALES Y MÉTODOS
Se presenta el fundamento teórico para resolver el problema de Flujos Óptimos de Potencia con Consideraciones Ambientales (FOPCA). Esto incluye un análisis de los combustibles y sus emisiones, la formulación matemática de los flujos óptimos AC, los costos de los combustibles y el factor de penalización por emisiones.
Los combustibles y sus emisiones
El aumento de emisiones de CO₂ relacionadas con la energía sigue en crecimiento, alcanzando un récord de más de 36.8 Gt en 2022 (IEA). Este incremento proviene principalmente del uso de carbón y petróleo en generación eléctrica y transporte, aunque las energías renovables han mitigado parcialmente este impacto al representar el 90% del crecimiento en generación de electricidad el último año [25].
La Tabla 1 muestra la relación entre el tipo de combustible y sus emisiones. Los combustibles sólidos, como el carbón, son altos emisores, mientras que los combustibles gaseosos y alternativas bajas en azufre, como el GNL, presentan menores emisiones. Las energías renovables y combustibles alternativos como biocombustibles y vehículos eléctricos representan opciones con menor huella de carbono [26-28].
En Ecuador, el Factor de Emisión de CO₂ del Sistema Nacional Interconectado se detalla en la Tabla 2, que presenta los valores de emisiones de CO₂ por tipo de combustible usado en el sector eléctrico.
Flujo óptimo de potencia AC
El flujo óptimo de potencia AC minimiza el costo de generación (Ecuación 1) considerando restricciones de balance de potencia activa y reactiva, límites de generación, voltaje, y flujo de potencia (Ecuaciones 2 a 7). Este modelo asegura una operación eficiente y segura del sistema eléctrico.
Descripción de Variables:
C 𝐢 𝑷 𝑮 𝒊 : Costo de generación
𝑷 𝒊, 𝑸 𝒊, : Potencia activa y reactiva en la barra 𝑖.
𝑷 𝑮 𝒊 , 𝑸 𝑮 𝒊 : Potencia activa y reactiva generada en la barra 𝑖.
𝑷 𝑫 𝒊 , 𝑸 𝑫 𝒊 : Demanda de potencia activa y reactiva generada en la barra 𝑖.
𝑽 𝒊 : Nivel de voltaje en la barra 𝑖.
𝑮 𝒊𝒋 , 𝑩 𝒊𝒋 : Conductancia y susceptancia entre las barras 𝑖 y 𝑗.
𝑺 𝒊𝒋 Flujo de potencia en la línea de transmisión entre las barras 𝑖 y 𝑗.
Costos de Combustible en Unidades Generadoras de Potencia
El costo de combustible se modela mediante una función cuadrática en función de la potencia generada (Ecuación 8), capturando la relación no lineal entre potencia y costo.
Pérdidas en líneas de transmisión
Las pérdidas en líneas de transmisión se calculan mediante la fórmula de pérdida de Kron (Ecuación 9), que considera las interacciones entre barras y pérdidas individuales del sistema.
Oscilaciones del costo de combustible
El efecto de punto de válvula, que introduce oscilaciones en el costo debido a la apertura y cierre de válvulas, se representa en la Ecuación 10.
Factor de penalización por emisiones
El factor de penalización (Ecuación 11) ajusta el costo de generación en función de las emisiones, integrando consideraciones ambientales en la optimización.
Algoritmo de búsqueda de cuervo (CSA)
El Algoritmo de Búsqueda de Cuervo (CSA) es una técnica de optimización basada en el comportamiento de los cuervos para ocultar comida, con mecanismos de exploración y explotación adaptativos. La posición y memoria de los cuervos se actualizan en cada iteración para buscar la solución óptima [31].
METODOLOGÍA
La metodología emplea el modelo FOPCA (Flujos Óptimos de Potencia con Consideraciones Ambientales) implementado en MATLAB (Figura 1). Este modelo se utiliza para optimizar tanto los costos de combustible como las emisiones de los generadores en un sistema de potencia eléctrica. Inicialmente, se definen los parámetros de entrada, incluyendo la función objetivo, restricciones de balance de potencia, potencia generada, emisiones y potencia nodal. Estos parámetros se procesan en MATLAB, generando resultados clave como el despacho de potencia activa y reactiva, el flujo de potencia por nodos, emisiones por generador, consumo de combustible y perfil de tensión. Los resultados permiten analizar la eficiencia y sostenibilidad del sistema. Para resolver el modelo FOPCA, se utiliza el algoritmo que sigue los pasos que se muestran en la tabla 3, misma que detalla el proceso de optimización mediante el algoritmo de búsqueda de Cuervo (CSA).
Es imporatnte mencioanar, que la metología propuesta presenta algunas ventajas, entre ellas la mejora de eficiencia energética y la integración de energías renovables. Es por ello que la optimización de flujos de potencia es una herramienta para mejorar la gestión eficiente de sistemas eléctricos, especialmente al incorporar energías renovables [29]. Sin embargo, uno de los problemas es la complejidad computacional, ya que los algoritmos de optimización no lineales, como el algoritmo de búsqueda de Cuervo, resulta costos en términos de recursos computacionales, y más aún cuando se aplican a redes de mayor escala [30].
Modelo FOPCA propuesto
El modelo busca minimizar los costos de generación y las emisiones de los generadores eléctricos, formulado como un problema de optimización no lineal dinámica. La función objetivo incluye términos de costo y de penalización por emisiones, representada en la Ecuación 12. Este enfoque permite optimizar las variables de generación y emisiones al integrar las restricciones del sistema.
Las restricciones del modelo garantizan que el sistema opere dentro de límites seguros y eficientes, tanto en términos de generación de potencia como en emisiones (Ecuaciones 14-19):
Balance de potencia: La ecuación de balance de potencia (Ecuación 18-19) asegura que la suma de las potencias generadas (Ecuación 14) iguale la demanda total 𝑃 𝑑 , ajustada por las pérdidas del sistema.
Límites de generación: La Ecuación 15 establece los límites de generación activa, asegurando que cada generador opere dentro de su capacidad.
Restricciones de potencia reactiva: La Ecuación 17 mantiene la estabilidad de voltaje en el sistema.
Límites de emisiones: La ecuación de emisiones (Ecuación 13) garantiza que cada generador mantenga sus emisiones bajo un límite máximo permitido.
Este modelo asegura la estabilidad y eficiencia del sistema eléctrico, integrando además consideraciones ambientales en el proceso de optimización.
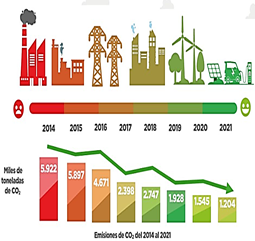
Proyección de emisiones de CO₂ en el sector eléctrico
En la Figura 2 se presenta la proyección de las emisiones de CO₂ en el sector eléctrico ecuatoriano entre 2014 y 2024. Las emisiones se han reducido significativamente gracias a la adopción de tecnologías más limpias y eficientes, pasando de 5,922 miles de toneladas en 2014 a una proyección de 181 miles de toneladas en 2024. Esta tendencia muestra el compromiso del sector con la sostenibilidad y la mitigación del cambio climático.
Para obtener esta proyección se aplicó un modelo de regresión lineal, considerando la reducción media anual en las emisiones de CO₂ (Ecuaciones 20-22).
Donde a es la pendiente y b la intercepción, calculados a partir de los datos históricos.
3.3 Descripción del sistema de estudio
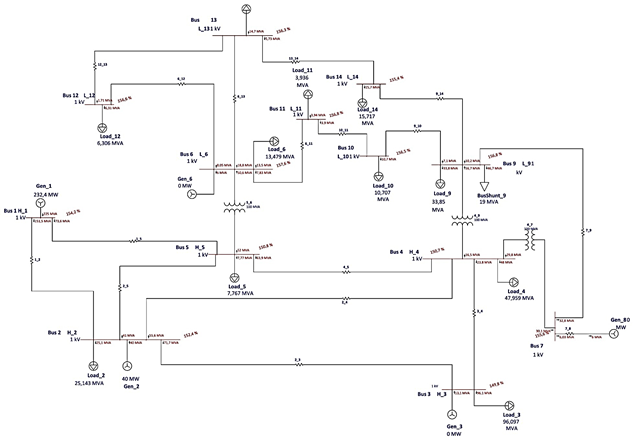
El sistema IEEE de 14 barras, que se presenta en la figura 3, se utiliza como modelo de estudio, permitiendo analizar la estabilidad y eficiencia del sistema bajo condiciones de optimización de costos y emisiones. Este sistema consta de 14 barras, 5 generadores y 11 líneas de transmisión. Además de los estudios de estabilidad, este modelo permite analizar los flujos óptimos de potencia en el contexto del modelo FOPCA.
La característica de los generadores se reportan en la Tabla 5, donde constan parámetros relevantes para cada tipo de generador utilizado en el sistema.
Adicional a lo mencionado anterirmente, se señala que el mdodelo propuesto se validó inicialmente en redes de tamaño moderado, pero, para evaluar su aplicabilidad en redes de mayor complejidad, por lo tanto se realizaron simulaciones utilizando el sistema IEEE 30 - barras y IEEE 57 - barras, estas representan redes eléctricas de mayor escala con una mayor cantidad de nodos, líneas de transmisión y generadores. Además estas redes, son comúnmente usadas para evaluar la optimización de flujos de potencia en sistemas eléctricos reales, esto permite un análisis más detallado y cercano a las condiciones operativas de un entorno real.
Las simulaciones se llevaron a cabo bajo condiciones normales de operación, se consideraron variaciones de demanda energética y los flujos de potencia dinámicos en distintas barras. Se empleó el algoritmo de búsqueda de Cuervo (CSA) con el fin de realizar la optimización, y en cada iteración se ajustaron las posiciones de los "cuervos", con el objetivo de minimizar costos de generación y las emisiones de CO2. Sus resultados se compararon con las simulaciones previas, mostrando un aumento significativo en la robustez y precisión del modelo al enfrentar escenarios más complejos.
Como punto a destacar, consta la inclusión de la generación distribuida (DER) en el sistema, con energía solar y eólica con el fin de hacer una evaluación al sistema. Los resultados reportaron que el algoritmo es capaz de mantener la eficiencia del sistema incluso con fluctuaciones en la producción de energía, optimizando tanto los costos como las emisiones de forma efectiva.
Un desafío adicional que se abordó en las simulaciones fue la congestión de las líneas de transmisión, este es un problema común en sistemas grandes, esto debido a la alta demanda energética y a la limitada capacidad de las redes. Este modelo fue capaz de encontrar soluciones óptimas que mantuvieron las restricciones de voltaje y capacidad de las líneas, demostrando su efectividad en escenarios de congestión. Además, las simulaciones demostraron la capacidad para optimizar el flujo de la potencia en redes con diversos generadores, minimizando así pérdidas y mejorando la estabilidad en el sistema.
El modelo propuesto se ha evaluado con total rigurosidad, se ha incluido recursos energéticos distribuidos (DER), como lo es la energía solar y la eólica, en varias simulaciones. Los resultados muestran que el Algoritmo de Búsqueda de Cuervo (CSA) es capaz de manejar eficazmente la variabilidad de la generación renovable. Dicho modelo optimiza costos de generación y las emisiones de CO2, inclusive cuando los DER tienen una alta penetración en el sistema. La flexibilidad del algoritmo permite ajustar el despacho de energía y mitigar fluctuaciones en la producción de energía renovable, lo que contribuye a mantener la estabilidad del sistema.
En condiciones de baja disponibilidad de los DER, el modelo prioriza la generación convencional, asegurando que el sistema no sufra interrupciones ni pérdidas significativas. Además, el algoritmo demuestra una capacidad destacable para optimizar el flujo de energía en situaciones de congestión de líneas de transmisión, asegurando que las fluctuaciones de los DER no afecten la operación eficiente del sistema.
RESULTADOS Y DISCUSIÓN
Análisis comparativo
En esta sección, se comparan los resultados del sistema IEEE de 14 barras en dos escenarios: sin restricciones de penalización y con restricciones de penalización. Los parámetros evaluados incluyen el perfil de tensión, potencia activa y reactiva nodal, emisiones totales y consumo de combustible. Este análisis permite entender cómo las restricciones de penalización afectan el rendimiento y sostenibilidad del sistema.
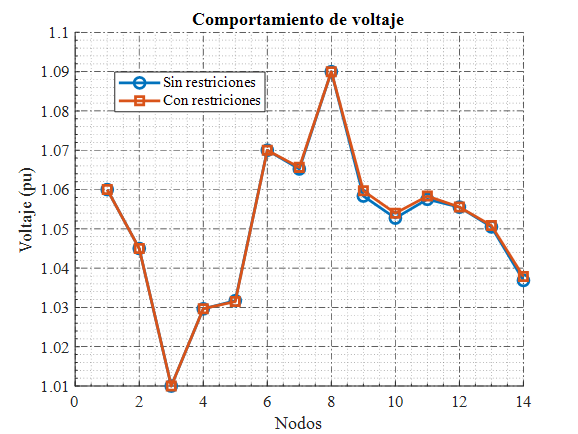
La Figura 4 muestra el comportamiento del voltaje en el sistema de 14 barras bajo ambas condiciones. Aunque la mayoría de los nodos mantienen niveles similares en ambos casos, se observan ligeras diferencias en los nodos 4, 5, 7, 9, 10 y 11, donde el voltaje disminuye levemente en el escenario con restricciones. Estas variaciones, aunque pequeñas, son relevantes para la estabilidad del sistema.
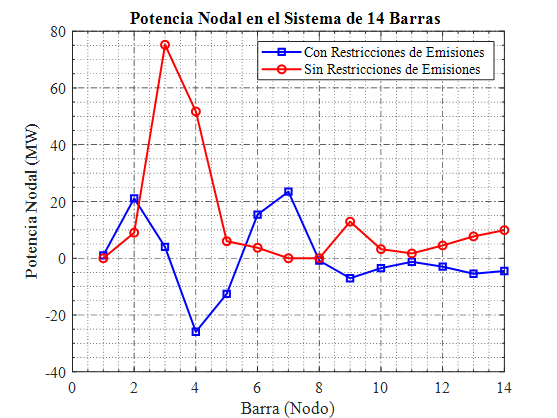
Se puede observar en la Figura 5 que ilustra la distribución de la potencia activa nodal en ambos escenarios. En el caso sin restricciones, los nodos 2, 3 y 5 presentan inyecciones de potencia más altas, especialmente el nodo 5. Bajo restricciones de emisiones, los niveles de potencia disminuyen, y algunos nodos, como el 4 y 5, registran valores negativos, indicando consumo en lugar de generación.
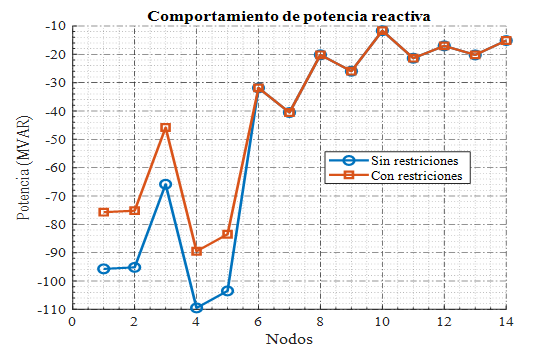
En la Figura 6 presenta la comparación de la potencia reactiva nodal en el sistema. Se observa que en los nodos 1 a 4, la potencia reactiva es más baja en el escenario sin restricciones, con diferencias significativas en nodos críticos como el nodo 4. A partir del nodo 5, las diferencias disminuyen, lo cual indica que las restricciones afectan principalmente a los primeros nodos.
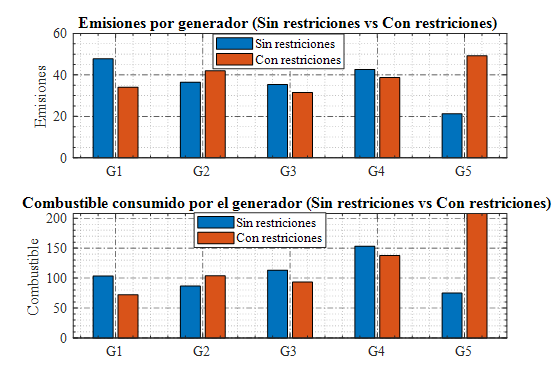
En la Figura 7 analiza las emisiones y el consumo de combustible de los generadores (G1 a G5) en ambos escenarios. Se observa una reducción de emisiones en G1, G3 y G4 en el escenario con restricciones, mientras que G2 y G5 aumentan sus emisiones. En términos de consumo de combustible, G1 y G3 disminuyen, mientras que G2, G4 y G5 aumentan, mostrando el impacto de las restricciones en la eficiencia operativa.
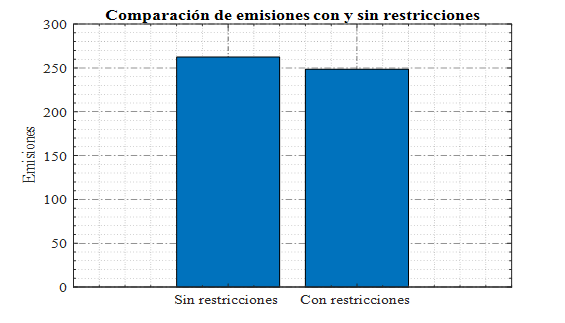
La Figura 8 compara las emisiones totales del sistema en ambos escenarios. En el caso sin restricciones, las emisiones alcanzan 262,45 unidades, mientras que con restricciones se reducen a 248,45 unidades, indicando una mejora en sostenibilidad debido a la implementación de restricciones.
4.2 Caso 1: Minimización de Costo sin Restricción de Emisiones
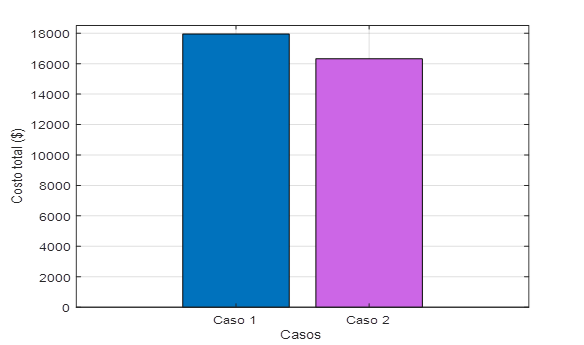
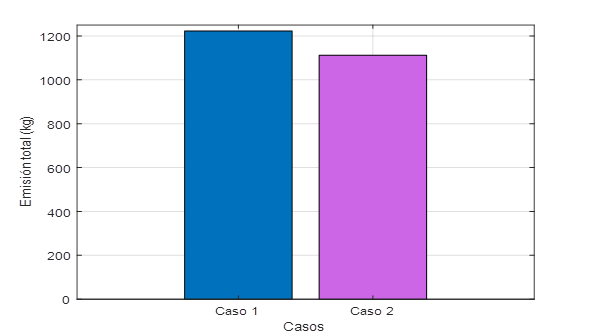
En este caso, se minimiza el costo total de generación sin considerar penalizaciones de emisiones. La Tabla 6 presenta los resultados, mostrando un costo total de $17,948.87 y emisiones de 1,222.77 kg. La potencia total generada es de 260.34 MW, distribuida entre los generadores de acuerdo a su capacidad y eficiencia.
4.3 Caso 2: Minimización de Costo con Penalización de Emisiones
En este caso, se minimiza el costo total considerando penalizaciones de emisiones. La Tabla 7 muestra los resultados, con un costo total de $16,317.16 y emisiones de 1,111.61 kg, lo que refleja una reducción tanto en costos como en emisiones en comparación con el Caso 1.
Tabla 7: Resultados del caso 2 correspondiente a la minimización de costo de generación considerando las penalizaciones por emisiones

La Figura 9 presenta una comparativa de los costos entre ambos casos, y la Figura 10 compara las emisiones totales, mostrando que el escenario con penalización es más eficiente en términos de costos y sostenibilidad ambiental.
5. CONCLUSIONES Y RECOMENDACIONES
Se ha logrado establecer un modelo matemático que relaciona los costos de generación y las emisiones de gases producidos por las centrales de generación. Este modelo ha sido utilizado en el proceso de optimización para determinar la distribución óptima de las potencias de los generadores, buscando minimizar tanto los costos de operación como las emisiones.
La metodología de flujo óptimo de potencia con consideración ambiental ha sido aplicada a casos de estudio específicos, como se muestra en las figuras presentadas. A través de estas aplicaciones, se ha evidenciado el efecto positivo de la optimización en la reducción de emisiones a lo largo de las iteraciones. Además, se ha mantenido la estabilidad de los costos de operación, demostrando la eficacia de la metodología en alcanzar los objetivos de eficiencia económica y sostenibilidad ambiental.
El Caso 2, demuestra un perfil de emisiones más bajo que el Caso 1, lo cual sugiere una mayor eficiencia ambiental. Esto podría deberse al uso de combustibles más limpios, una mayor participación de energías renovables en la matriz energética, o una operación y mantenimiento más eficientes de los equipos de generación.
La diferencia en las emisiones entre los dos casos podría tener implicaciones significativas en términos de cumplimiento regulatorio, especialmente en jurisdicciones con estrictas políticas de emisiones. El Caso 2 podría beneficiarse de incentivos por bajas emisiones, mientras que el Caso 1 podría enfrentar tarifas o sanciones más altas debido a su mayor impacto ambiental.
El Caso 1 incurre en un costo total más alto que el Caso 2. Esto sugiere que las prácticas de operación, la eficiencia de los generadores, el precio del combustible utilizado o la mixtura energética en el Caso 1 son menos favorables desde el punto de vista económico en comparación con el Caso 2. Esta diferencia en los costos totales podría justificar una evaluación detallada de las estrategias de operación y de la gestión de activos para identificar áreas de mejora y reducir costos en futuros periodos operativos.
Se recomienda implementar estrategias de optimización de costos y emisiones en la planificación operativa de las plantas de generación a largo plazo. Dado que el modelo matemático optimiza la distribución de potencia minimizando tanto costos como emisiones, su aplicación permitirá una gestión más eficiente de los recursos y contribuirá al cumplimiento de los objetivos económicos y ambientales, garantizando un sistema de generación más sostenible.
Es fundamental promover el uso de energías renovables y combustibles más limpios en la matriz energética. Los resultados del Caso 2, que demuestran un menor impacto ambiental, sugieren que la incorporación de estas fuentes podría reducir significativamente las emisiones y mejorar la eficiencia operativa. Además, el aumento de la participación de energías renovables maximizará los beneficios ambientales y permitirá acceder a posibles incentivos gubernamentales.
Para mejorar la eficiencia y reducir costos operativos, se recomienda ajustar la política de mantenimiento y operación de los generadores. La diferencia en los costos entre los casos muestra la importancia de una operación y mantenimiento efectivos. Por lo tanto, un programa de mantenimiento preventivo y predictivo en los generadores, con especial enfoque en aquellos con mayor consumo de combustible y emisiones, es crucial para optimizar su rendimiento y minimizar costos.
Es importante evaluar el impacto de las restricciones ambientales en el diseño de estrategias de despacho de carga, ya que las restricciones de penalización por emisiones influyen significativamente en el comportamiento del sistema. Considerar estas limitaciones en la planificación podría facilitar el cumplimiento de políticas de emisiones estrictas, evitando sanciones y accediendo a incentivos económicos por mantener bajas emisiones en el sistema de generación.
Por último, la metodología utilizada en este estudio podría servir como base para desarrollar modelos de simulación que permitan a los reguladores evaluar el impacto de diferentes políticas ambientales y tarifas en el sector eléctrico. Esto contribuirá a la toma de decisiones informadas y permitirá crear incentivos efectivos que promuevan prácticas sostenibles en la generación de energía, beneficiando tanto al medio ambiente como a la economía del sector.