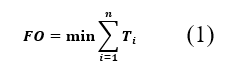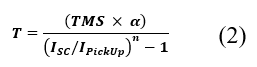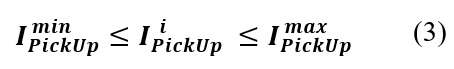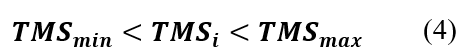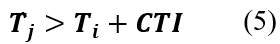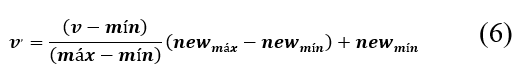INTRODUCCIÓN
Asegurar el suministro continuo y la calidad de la energía eléctrica es indispensable, puesto que, permite el desarrollo de las actividades que incluyen el uso de esta energía. Las fallas pueden ocurrir a cualquier instante y en cualquier punto del sistema eléctrico, por esto, se deben incorporar sistemas de protección para mitigar los daños y salvaguardar a los operadores del sistema. Las protecciones de sobrecorriente son muy utilizadas, debido a su bajo costo y la facilidad para su operación. Los relés de sobrecorriente permiten despejar las fallas de forma oportuna, para lo cual, se debe optimizar el ajuste que permita disminuir los tiempos de operación manteniendo una adecuada coordinación entre los relés [1].
En la literatura se han presentado varios métodos para optimizar la coordinación de relés de sobrecorriente [1]. Para este trabajo se utiliza el algoritmo COA (Cuckoo Optimization Algorithm) y el algoritmo GSA (Gravitational Search Algorithm) para obtener la coordinación óptima del sistema eléctrico de prueba de 13 nodos de la IEEE, en el que se le incorpora dos relés. Se presenta una comparación de cada algoritmo de optimización con el ajuste tradicional propuesto para este trabajo y finalmente se presenta una comparación entre algoritmos. La optimización se realiza únicamente a los relés 51.
El algoritmo COA, desarrollado por Ramin Rajabioun y presentado en [2], ha sido propuesto en varios artículos para resolver diferentes problemas gracias a su amplia aplicabilidad. Este algoritmo corresponde a un método heurístico capaz de encontrar soluciones óptimas de manera eficiente mediante la búsqueda de nuevos óptimos globales sin converger prematuramente en óptimos locales. En [3] se implementa el algoritmo COA para optimizar el pronóstico del consumo de la demanda de energía en Irán mediante indicadores socioeconómicos, cuyos resultados son adecuados. En [4] se optimiza en la misma función objetivo al Intervalo de Tiempo de Carga (CIT) y las pérdidas de energía (EL) de una batería de litio-ion, tomando como método de optimización el algoritmo COA, obteniendo resultados favorables. En [1] se implementa la optimización de relés de sobrecorriente en el sistema de 8 barras mediante el algoritmo COA, se consiguen mejoras significativas en el ajuste de los relés.
El método de optimización GSA fue desarrollado por E. Rashedi, H. Nezamabandi-pour y S. Saryzdi. Se basa en la ley de gravitación universal propuesta por Isaac Newton en 1687 dentro de su obra Philosophiae Naturalis Principia Mathematica en la cual se establece que la fuerza de atracción entre dos cuerpos de diferente cantidad de masa depende completamente del tamaño y la distancia que las separa [5].
Haciendo un símil entre la ley de gravitación universal y el algoritmo heurístico GSA la solución óptima corresponde a aquella que genera mayor atracción entre las masas obtenidas a partir de agentes aleatorios evaluados en la función objetivo dentro del espacio de búsqueda establecido [5].
El GSA aparece por primera vez en [6] donde se establece la metodología a seguir para la aplicación del algoritmo de optimización y se complementa con la implementación en MATLAB por parte de uno de los autores (Esmat Rashedi). En el algoritmo propuesto se tiene un catálogo de funciones de prueba (Benchmark functions) para poder validar el funcionamiento del algoritmo y su capacidad de obtener una respuesta optimizada [7].
Este método es muy versátil, puesto que, se aplica en diferentes áreas de estudio incluido el campo de protecciones eléctricas. Una de las aplicaciones se desarrolla en [8] donde se aplica el GSA para optimizar un sistema de protecciones de sobrecorriente temporizadas en un sistema con generación distribuida teniendo resultados positivos.
METODOLOGÍA
Para la optimización de los relés de sobrecorriente temporizados (51) se utilizan los algoritmos COA y GSA empleando la corriente de cortocircuito más probable obtenida a través de la simulación de Montecarlo. Para realizar la optimización, se modelan los relés de sobrecorriente en un sistema de prueba en PowerFactory. Los algoritmos son codificados en Python. A través del sistema de prueba del software PowerFactory los códigos de cada algoritmo son ejecutados para realizar la optimización. Los ajustes óptimos obtenidos, correspondientes a cada algoritmo, son comparados con los ajustes tradicionales de los relés 51 del sistema de prueba. Finalmente se realiza una comparación entre los ajustes óptimos obtenidos de cada algoritmo.
Corrientes más probables a partir de la simulación de Montecarlo
Se realiza la estimación de la corriente de cortocircuito más probable en el área de coordinación de las protecciones eléctricas. Se emplea una función de distribución normal para estimar los valores de las cargas, y una uniforme para seleccionar el tipo de cortocircuito, la resistencia de falla y la ubicación del cortocircuito.
Se evalúan los cortocircuitos trifásico, bifásico, bifásico a tierra y monofásico. La resistencia de falla varía entre cero y tres ohmios, y la ubicación del cortocircuito se selecciona para propender la operación de las protecciones temporizadas.
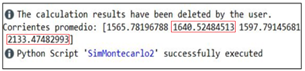
Se aplican 10.000 simulaciones de Montecarlo y se obtienen las corrientes más probables, con las cuales se ejecutarán los algoritmos de optimización. En la Fig. 1 se observan los resultados de las corrientes para cada fase obtenidas de la simulación de Montecarlo en el software PowerFactory.
Algoritmo de Optimización Cucú (Cuckoo Optimization Algorithm - COA)
El algoritmo COA inicializa las variables de decisión, las cuales son almacenadas dentro de un vector de variables que el algoritmo define como hábitat. Se inicializan varios hábitats, cada hábitat corresponde a un nido de ave cucú madura, en donde, se lo define como centro de puesta de huevos. Cada cucú maduro puede poner de entre 5 a 20 huevos dentro de un radio máximo definido como el ELR (Egg Laying Radious) desde el centro de puesta de huevos propio de cada ave cucú madura. Cada hábitat formado por sus correspondientes variables de decisión es visto por el algoritmo como la posición de cada cucú, y las posiciones de los cucús no pueden ser repetidas. El algoritmo inicializa los hábitats con valores aleatorios y, además, define el número de huevos de cada cucú y sus posiciones también de forma aleatoria [2].
La posición de los cucús maduros y los cucús crías son almacenados dentro de una matriz. Mediante la función objetivo implementada como parte del algoritmo COA, se evalúan todos los hábitats de cucús almacenados en la matriz. Se consigue la evaluación de todas las posiciones de los cucús de la matriz, con lo que, se puede clasificar según su evaluación y eliminar a los que consiguen las peores evaluaciones. El algoritmo COA implementa el método de clustering K-Means para separar entre grupos que tengan posiciones similares, a estos grupos se los define como sociedades. Entre las sociedades se determina la mejor posición de cucú, que tiene la mejor evaluación entre todas las posiciones de los cucús de la matriz y se la define como punto objetivo de llegada para los otros cucús. Los cucús migran hacia una nueva posición, buscando acercarse al punto objetivo de llegada [2].
La matriz que contiene la posición de los cucús es actualizada por sus nuevas posiciones conseguidas después de la migración efectuada. Las nuevas posiciones se redefinen como centro de puesta de huevos para la nueva generación de cucús maduros. El algoritmo comienza una nueva iteración a partir de la nueva matriz, de este modo se repite el número de iteraciones programadas por el algoritmo. En cada iteración, el algoritmo realiza la búsqueda de nuevas posiciones de cucús que alcancen mejores evaluaciones que las encontradas en las anteriores iteraciones. Al realizar la búsqueda de nuevas posiciones de manera aleatoria, permite que el algoritmo no defina a óptimos locales como óptimos globales [2].
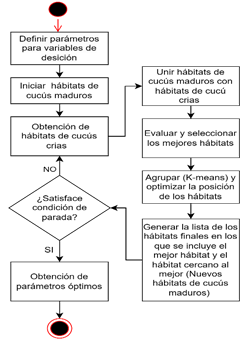
En la Fig. 2 se presenta el diagrama de flujo del algoritmo COA.
Algoritmo de Optimización GSA (Gravitational Search Algorithm - GSA)
El GSA requiere la inicialización de parámetros para ser utilizados en la definición del espacio de búsqueda, el número de iteraciones, dimensión de la función objetivo y el número de agentes aleatorios a evaluar. Con los datos ingresados se calculan las restricciones para establecer el espacio de búsqueda y encontrar los agentes aleatorios.
Este paso inicial permite al algoritmo hallar valores necesarios para realizar la comparación con los cálculos posteriores dentro del proceso iterativo e ir optimizando el resultado. Para dar inicio al algoritmo de búsqueda gravitacional son necesarios los agentes iniciales, la solución ligada a estos agentes, los arreglos de aceleración, velocidad, posición, la constante gravitatoria, el mejor valor, el peor valor y la masa.
Los agentes iniciales se obtienen de manera aleatoria dentro del espacio de búsqueda establecido. Estos agentes son evaluados en la función objetivo obteniendo así la solución con un menor error.
Seguidamente se realizan los cálculos para la obtención del arreglo de masas utilizando el mejor y peor valor. Se normaliza el vector obtenido y a continuación se calcula la contante de gravitación G que permite realizar un control en la precisión en la exploración. Para ejecutar el cálculo se utilizan las constantes α y G0, la iteración actual y el número máximo de iteraciones.
Considerando los valores obtenidos se procede a realizar el cálculo de la aceleración entre campos gravitacionales. Para conseguir este valor se realiza un control de mejores agentes considerando un porcentaje establecido por el usuario, el número de iteración actual y el total de iteraciones. A continuación, se calcula la fuerza utilizando la constante gravitatoria, el producto cruz entre los vectores de masas activas y pasivas, y la distancia entre las masas involucradas.
Con los valores de aceleraciones para las diferentes masas se realiza el cálculo de nuevos arreglos de posiciones y velocidades. Esta se considera como la primera iteración, puesto que se aplica el proceso completo del GSA, pero se diferencia de las iteraciones siguientes en que la solución hallada no se compara para ser optimizada.
Los datos hallados en esta primera iteración se ingresan en el proceso iterativo y se repite el proceso utilizando nuevos agentes aleatorios y comparando las soluciones siguientes con las halladas en iteraciones posteriores. El algoritmo finaliza al llegar a la última iteración y devuelve el resultado óptimo para ser configurados en los relés de sobrecorriente, es decir, el valor de dial de tiempo, la corriente de ajuste y el tipo de curva para cada relé que conforma el sistema de protecciones.
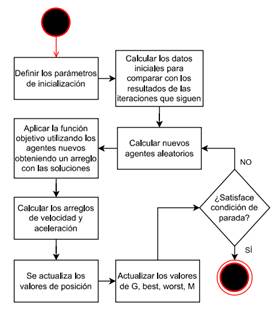
En la Fig. 3 se presenta el diagrama de flujo del algoritmo GSA.
Sistema de prueba de 13 nodos de la IEEE
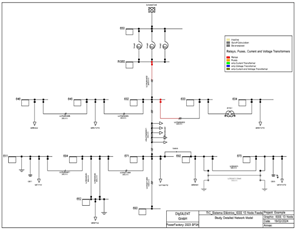
Este es un sistema de prueba presentado por primera vez en [9]. En [10] se modela en el software PowerFactory dentro de su biblioteca de ejemplos, con algunos casos de estudio. El caso de estudio que se utiliza en este trabajo es el Study Detail Network Model, dado que, en este caso de estudio se encuentra el modelo detallado del sistema de prueba. Este sistema eléctrico presenta circuitos trifásicos, bifásicos y monofásicos con cargas desbalanceadas. Este es un sistema eléctrico de distribución con una frecuencia de 60 [Hz], conectado de forma radial, como se puede apreciar en la Fgura Fig. 4.
Modelación de relés de sobrecorriente en el sistema de prueba
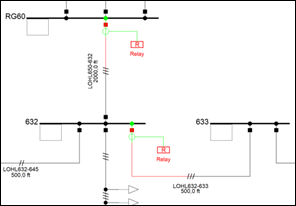
Se introducen dos relés de sobrecorriente 50/51 de fase dentro del sistema de prueba de 13 nodos de la IEEE. El primero es colocado en la entrada del alimentador troncal LOHL650-632 en el lado del nodo RG60, por facilidad se nombra a la característica instantánea como relé “50_RG60”, a la característica temporizada se la nombra relé “51_RG60” y para referirse a ambas características se nombra como “RG60”.
El segundo relé es colocado en el alimentador ramal LOHL632-633 en el lado del nodo 632, por facilidad se nombra a la característica instantánea como relé “50_632”, a la característica temporizada se la nombra relé “51_632” y para referirse a ambas características se nombra relé “632”.
Se utiliza un TC de 25 VA 10P20 para transformar de amperios primarios a amperios secundarios a la corriente de falla para cada relé 50/51. Para el relé RG60 se selecciona una relación de transformación de 1000/5, mientras que, para el relé 632 se selecciona una relación de 500/5.
En la Fig. 5 se pueden apreciar los relés modelados dentro del sistema de prueba.
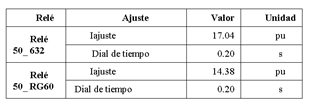
Al realizar el ajuste de los relés mediante criterios tradicionales, tomados de [11], se obtienen los parámetros de ajuste presentados en las Tablas 1 y 2.
En la Tabla 1 se presenta el ajuste efectuado con criterios tradicionales para los relés instantáneos, este ajuste es considerado como ajuste definitivo, porque no se realiza la optimización de la característica 50 de estos relés.
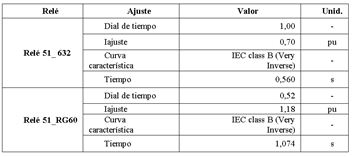
La Tabla 2 presenta el ajuste efectuado con criterios tradicionales de los relés temporizados. Este ajuste se lo considera como ajuste base, dado que, a partir de este se determinan las mejoras conseguidas con el ajuste óptimo de cada algoritmo.
Al implementar el ajuste de los relés 50/51 RG60 y 632 en el sistema de prueba del alimentador troncal y del ramal respectivamente, se obtienen las curvas de tiempo - corriente descritas en la Fig. 6.
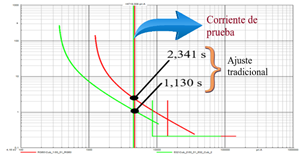
Figura 6: Curvas características de los relés RG60 y 632 con el cálculo de la corriente de ajuste del relé 51_RG60
En la -Fig. 6 se observa la curva característica de los relés RG60 y 632 de color rojo y verde, respectivamente. También se muestran los tiempos de operación de 2,341 y 1,130 [s] para cada relé al calcular una corriente de prueba.
La corriente de prueba que se implementa para comparar el tiempo de operación de las protecciones ajustadas con criterios tradicionales y, posteriormente, con el ajuste óptimo corresponde a una corriente monofásica sin impedancia de falla en el nodo 633.
Función Objetivo
Para resolver el problema de ajuste óptimo para relés de sobrecorriente existen algunas propuestas publicadas. Para este trabajo se propone como función objetivo la suma total de tiempos de operación y sus restricciones, que se presenta en [12]. Mediante la ecuación (1) se presenta la función objetivo utilizada en este trabajo:
Para calcular el tiempo de operación de cada relé, se implementa la ecuación de la curva característica según el estándar IEC [12]. La ecuación de la curva característica de la IEC se presenta en (2).
Donde:
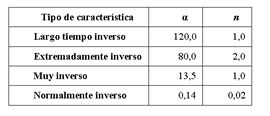
En la Tabla 3 se presentan las constantes que definen el tipo de curva característica según el estándar IEC.
Los relés de sobrecorriente temporizados (51) deben ser ajustados mediante las variables de decisión, las cuales son el dial de tiempo, la corriente de ajuste o tap y el tipo de curva mediante las constantes 𝛼 y 𝑛. La corriente de falla es una variable de prueba que se utiliza para calcular el tiempo de operación de cada relé. Al simular una falla en el sistema eléctrico de prueba, se calcula la corriente de falla vista por cada relé.
Tabla 3: Constantes para diferentes características de operación del relé de sobrecorriente (Estándar IEC)
El ajuste adecuado de las protecciones permite despejar las fallas de forma oportuna, sin embargo, se debe optimizar los tiempos de operación de los relés y mantener la coordinación entre estos para mitigar las consecuencias de las fallas en el sistema. Al utilizar la ecuación de la curva característica con los parámetros de ajuste de cada relé y la corriente de falla correspondiente, se obtiene el tiempo de operación de cada relé. Mediante la ecuación (1) se obtiene el tiempo total de operación de todos los relés dado por el hábitat correspondiente. El algoritmo COA evalúa varios hábitats y converge hacia el mejor hábitat.
Restricciones
Las restricciones dentro de la función objetivo permiten descartar los valores que salen de rango para las variables de decisión. Para resolver el problema de coordinación óptima entre relés de sobrecorriente temporizados (51), existe tres restricciones principales que deben ser aplicadas. Las dos primeras restricciones corresponden al ajuste de los relés implementados en el sistema de prueba, las cuales son: límite superior e inferior de la corriente de ajuste y del dial de tiempo. La tercera restricción corresponde al tiempo de coordinación entre relés, en donde debe existir un Intervalo de Tiempo de Coordinación (CTI) entre el tiempo de operación de los relés.
En (3) se presenta la restricción de la corriente de ajuste, la cual no puede ser menor a la corriente de ajuste mínima ni mayor a la corriente de ajuste máxima. La corriente de ajuste mínima debe ser mayor a la corriente de flujo de potencia en demanda pico, para que la protección no opere en condiciones normales de operación del sistema. Al mismo tiempo, debe ser menor a la corriente de falla mínima, para que sea lo suficientemente sensible hacia la ocurrencia de fallas.
En (4) se presenta la restricción del dial de tiempo, en donde, al caer fuera del límite inferior o del límite superior, se descarta el hábitat dentro de la optimización. El dial representa el espacio que recorren los contactos del relé para operar, al aumentar el espacio también aumenta el tiempo de operación del relé. Para este trabajo se consideran los límites establecidos en el software PowerFactory de 0,05 y 1 para el límite inferior y superior, respectivamente.
La ecuación (5) muestra la restricción de coordinación entre relés, en donde, se debe verificar que el tiempo de operación de los relés de respaldo 𝑇 𝑗 sean mayores a la suma de CTI junto con el tiempo de operación del relé coordinado aguas abajo 𝑇 𝑖 . Según [12], el valor del CTI varía entre 0,2 y 0,5 segundos para asegurar la operación adecuada entre relés. Si no se cumple esta restricción, se puede dar el caso en el cual los relés operen antes de lo esperado, dejando sin servicio a más carga de la requerida.
Condiciones iniciales del algoritmo COA
Para iniciar los hábitats de cucú maduros, el algoritmo COA tiene parámetros que permiten inicializar las variables de decisión. Para introducir los parámetros requeridos del algoritmo, se debe conocer el problema a resolver y sus variables de decisión. En este trabajo se optimiza el ajuste de los relés de sobrecorriente temporizados (51), cada relé tiene tres variables de decisión las cuales son la corriente de ajuste, el dial de tiempo y el tipo de curva. Se modelan dos relés 51 en el sistema de prueba, el número total de variables de decisión que optimizará el algoritmo es de seis. En la Fig. 7 se presentan los parámetros principales que se deben definir en el algoritmo para llevar a cabo la optimización.
Se observa que el límite inferior y superior de las variables de decisión establecidos son cero y uno, respectivamente. Además, se inicializa diez cucús maduros. A lo largo de cada iteración del algoritmo, los cucús maduros pueden poner entre cinco a veinte huevos. Se forman tres sociedades de toda la población de cucús, con el método K-Means. Se limita a cien el número máximo de iteraciones en donde el algoritmo obtiene sus parámetros óptimos.
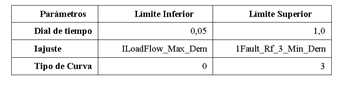
Las variables de decisión toman valores aleatorios que se encuentran entre varLo y varHi. Es necesario obtener el valor de la variable entre sus propios límites para poder evaluar el tiempo de operación del relé mediante la ecuación (2). Por tal razón, se debe llevar a los nuevos límites a las variables de decisión, estos nuevos límites se presentan en la Tabla 4.
Donde:
ILoadFlow_Max_Dem es la corriente del flujo de potencia a demanda máxima.
IFault_RF_3_Min_Dem es la corriente de falla mínima a demanda mínima.
Se utiliza la ecuación de normalización Min-Max para realizar el cambio de límites a las variables de decisión, mostrada en (6), obtenida de [13].
Donde:
Una vez realizado el cambio de límites, es posible evaluar las variables de decisión con la ecuación (2), y obtener el tiempo de operación.
Condiciones iniciales del algoritmo GSA
De la misma forma que en el algoritmo anterior, en el GSA se introducen los parámetros iniciales. Se optimizan variables similares para ajustar los relés de sobrecorriente temporizados (51) modelados en el sistema.
En la Fig. 8 se observan los parámetros necesarios para que el GSA, aplicado en la optimización de protecciones de sobrecorriente, pueda iniciar. Se incluye el número de agentes aleatorios en cada iteración, la dimensión de la función objetivo que considera solo los diales de tiempo y las corrientes de ajuste porque el tipo de curva se optimiza dentro del algoritmo y los límites superiores e inferiores para cada relé del sistema de protecciones.
Al igual que en el algoritmo COA, se utilizan los datos de la Tabla 4 para establecer los límites que definen el espacio de búsqueda para las variables a optimizar.
RESULTADOS
A través de la metodología descrita se consigue el ajuste óptimo de los relés, cuyos resultados y casos de estudio se presentan en las subsecciones 3.1 y 3.2.
Parámetros óptimos del COA y el GSA
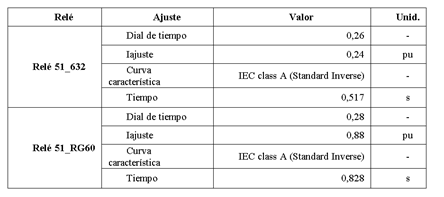
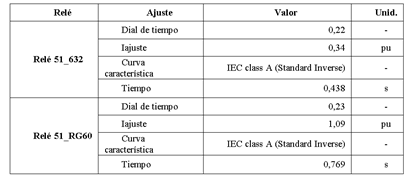
En la Tabla 5 se muestran los parámetros encontrados para la coordinación óptima utilizando el método COA, mientras que, en la Tabla 6 se presentan los parámetros optimizados utilizando el GSA. También se pueden observar los datos de los tiempos de operación en el punto de intercambio entre las características instantáneas y temporizadas.
Casos de estudio
Caso 1: Evaluación de los resultados del COA y GSA ante una falla monofásica franca
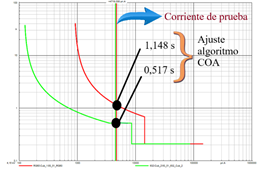
Al introducir el ajuste de la Tabla 5 en los relés 51 del sistema de prueba, se obtienen los tiempos de operación de 1,148 y 0,517 [s] de cada relé, al calcular la corriente de prueba. En la Fig. 9 se presentan los tiempos de operación de cada relé en su correspondiente curva característica aplicando el algoritmo COA.
Se ha conseguido reducir el tiempo de operación del ajuste tradicional (Fig. 6) para los relés RG60 y 632 de 2,341 a 1,148 [s] y de 1,130 a 0,517 [s], respectivamente. Disminuyendo 1,193 [s] (reducción del 50,97 %) y 0,613 [s] (reducción del 54,25 %) en la operación de cada relé. Para comprobar la coordinación correcta entre relés, se calculan los tiempos de operación a partir de la corriente de ajuste del relé 50_632. En todos los relés se cumple la condición de coordinación entre relés. El relé 50_632 opera a los 210 [ms], a los 517 [ms] opera el relé 51_632 y a los 828 [ms] opera el relé 51_RG60. Cada relé tiene un CTI de aproximadamente 300 [ms] de espera después de la operación del relé aguas abajo para operar, cumpliendo con la restricción de coordinación.
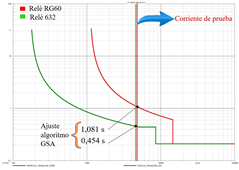
Al realizar el ajuste utilizando los parámetros mostrados en la Tabla 6 correspondientes a la coordinación de los relés de sobrecorriente temporizados obtenidos mediante el GSA y simulando una falla monofásica franca en la barra 633, se alcanzan los tiempos de operación de 1,081 [s] y 0,454 [s] para los relés RG60 y 632, respectivamente. En la Fig. 10 se presentan los tiempos de operación de cada relé con su correspondiente curva característica para la optimización efectuada con el algoritmo GSA.
Se ha conseguido reducir el tiempo de operación del ajuste tradicional obtenido de la corriente de prueba a los relés RG60 y 632 de 2,341 [s] a 1,081 [s] y de 1,130 a 0,454 [s], respectivamente. Disminuyendo 1,260 [s] (reducción del 53,82 %) y 0,676 [s] (reducción del 59.82 %) en la operación de cada relé.
Al igual que con los resultados del algoritmo anterior, se comprueba que la coordinación sea correcta. El relé 50_632 actúa a los 210 [ms], el relé 51_632 se activa a los 438 [ms] y el relé 51_RG60 a los 769 [ms]. Con ello, se comprueba que el CTI aproximado sigue siendo cercano a los 300 [ms], por lo que, se cumple con la restricción de la coordinación.
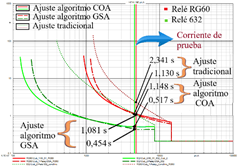
Figura 11: Resultados del caso 1 con los ajustes óptimos de los algoritmos COA y GSA, y el ajuste tradicional
En la Fig. 11 se observan en una misma gráfica los ajustes óptimos del algoritmo COA y GSA, junto al ajuste tradicional. Se simula la corriente de prueba para determinar el tiempo de operación resultante de cada relé modelado en el sistema eléctrico. La sumatoria de los tiempos de operación dados por el ajuste del algoritmo COA, obtenidos en los relés RG60 y 632 de 1,148 y 0,517 [s] respectivamente, es de 1,665 [s]. Los relés ajustados con los parámetros óptimos obtenidos del algoritmo GSA con tiempos de 1,081 y 0,454 [s] correspondiente a cada relé, presentan una sumatoria de tiempos de 1,535 [s]. Para esta falla, la sumatoria de los tiempos de operación resulta ser ligeramente menor al emplear los ajustes óptimos del algoritmo GSA. Ambos algoritmos consiguen reducir los tiempos de operación del ajuste tradicional (sumatoria de tiempos del ajuste tradicional: 3,471 [s]), manteniendo la coordinación entre relés.
Caso 2: Evaluación de los resultados del COA y GSA ante una corriente de falla monofásica con resistencia de falla a demanda mínima, al 10 % del alimentador LOHL632-633
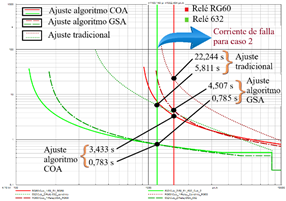
En la Fig. 12 se presenta el ajuste óptimo de los relés RG60 y 632 con líneas continuas y el ajuste tradicional con líneas entrecortadas empleando el algoritmo COA. Se calcula una falla monofásica con una resistencia de falla de dos ohmios a demanda mínima, producida al 10 % del alimentador. Se observa que el tiempo de operación es menor con la optimización, considerando para esta comparación el ajuste tradicional, reduciendo de 22,244 a 3,433 [s] y de 5,811 a 0,783 [s], para cada relé.
En la Fig. 13 se presenta el ajuste óptimo de los relés RG60 y 632 con líneas continuas y el ajuste tradicional con líneas entrecortadas. Se simula una falla con las mismas condiciones que en el caso de la Fig. 12. Se puede observar que se reducen los tiempos de operación teniendo una disminución de 22,244[s] a 4,507 [s] para el relé RG60 y de 5,811 [s] a 0,785 [s] para el relé 632.
En la Fig.14 se observa que la sumatoria de tiempos de operación dado por el ajuste del algoritmo COA, obtenido en los relés RG60 y 632 de 3,433 y 0,783 [s], respectivamente, es de 4,216 [s]. Los relés ajustados con los parámetros óptimos obtenidos del algoritmo GSA con tiempos de 4,507 y 0,785 [s] correspondiente a cada relé, presentan una sumatoria de tiempos de 5,292 [s].
Se observa que, para este tipo de falla, el algoritmo COA consigue un menor tiempo de operación que el GSA. Los tiempos de operación que consiguen los ajustes de ambos algoritmos, reducen significativamente los tiempos de operación del ajuste tradicional (sumatoria de tiempos del ajuste tradicional: 28,055 [s]), y mantienen la operación coordinada entre relés.
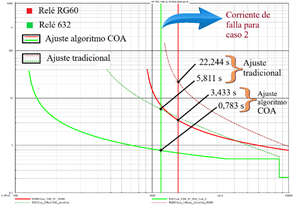
Figura 12: Tiempo de operación de los relés 51 con ajuste óptimo y ajuste tradicional, para la corriente de falla del caso 2, con el algoritmo COA
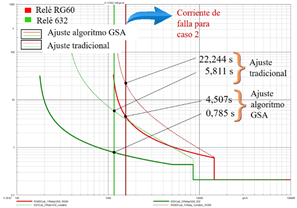
Figura 13: Tiempo de operación de los relés 51 con ajuste óptimo y ajuste tradicional, para la corriente de falla del caso 2, con el algoritmo GSA
CONCLUSIONES
En este trabajo se ha conseguido obtener una disminución en los tiempos de operación de los relés RG60 y 632 al implementar el ajuste óptimo obtenido por los algoritmos COA y GSA, en comparación con el ajuste tradicional. Se observa que los parámetros óptimos de ajuste que se obtiene con el algoritmo COA consiguen menores tiempos de operación para fallas menos sensibles, mientras que, el algoritmo GSA consigue menores tiempos para fallas más sensibles. Por lo tanto, los algoritmos implementados se constituyen en herramientas de gran utilidad para su aplicación en el diseño de sistemas de protecciones utilizando relés de sobrecorriente.
Con la aplicación desarrollada se mejoran las propiedades de sensibilidad y rapidez del sistema de protecciones, a la vez que se mantiene una adecuada coordinación y selectividad de los relés. Esto se traduce en una mayor seguridad para los operadores del sistema eléctrico, y favorece la mitigación de las consecuencias contraproducentes causadas por fallas de cortocircuito, como el daño de equipos y la disminución de su vida útil en la zona de protección.
Se comparte la lógica de programación desarrollada con la comunidad científica a través del enlace: https://drive.google.com/drive/folders/1HNkHKLELc0rSgsZExuqHvZPFut2CMDQ3?usp=sharing