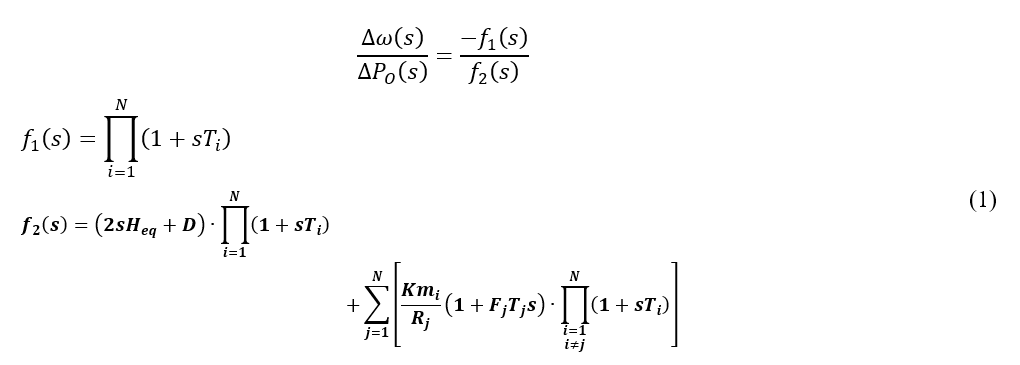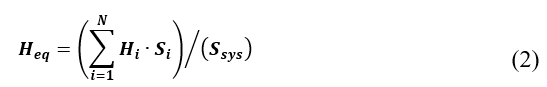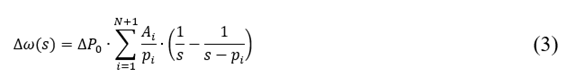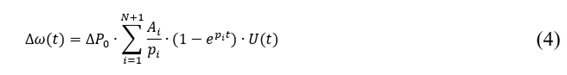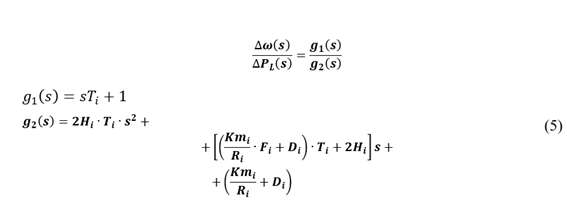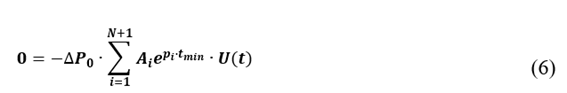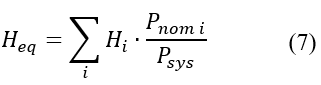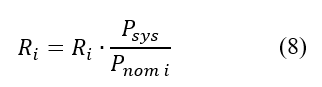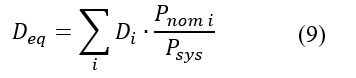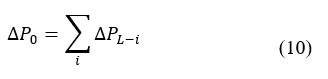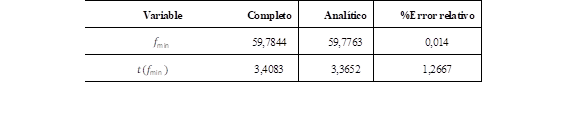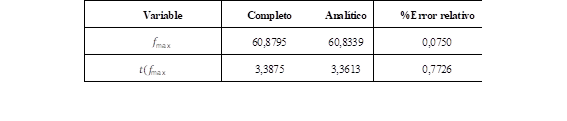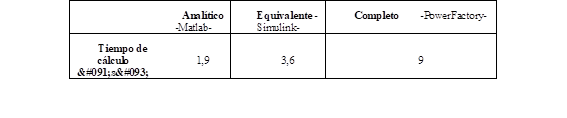INTRODUCCIÓN
La frecuencia es una variable fundamental del Sistema Eléctrico de Potencia ( SEP ) que refleja el estado del balance generación - carga. Cuando ocurre una falla que ocasiona la pérdida de generación o carga, pueden ocurrir grandes variaciones de frecuencia que deben ser controladas mediante la acción de los reguladores de velocidad asociados a los generadores y/o esquemas de alivio de carga. Si estas acciones de control no son suficientes para evitar la caída abrupta de la frecuencia, el SEP puede separarse en islas de forma incontrolada o llegar al colapso [1]. Estos problemas de estabilidad de frecuencia pueden desarrollarse en el marco de tiempo de segundos o fracciones de segundo (fenómenos de corto plazo) o pueden involucrar tiempos del orden de las decenas de segundo y hasta varios minutos (fenómenos de largo plazo) [2].
Parámetros importantes en la dinámica de la frecuencia, luego de un desbalance generación - carga, son: la frecuencia mínima (nadir) y el tiempo que demora el SEP en alcanzar dicha frecuencia. Los valores que alcanzan estas variables están relacionados con el tamaño del disturbio (MW perdidos de generación o carga) y las características dinámicas de los generadores y la carga, principalmente [3]. Usualmente, el nadir de la frecuencia y su tiempo de ocurrencia se determinan mediante simulaciones en el dominio del tiempo realizadas fuera de línea que, dependiendo del tamaño del SEP, pueden ser costosas desde el punto de vista computacional, con altos tiempos de ejecución.
En la operación en tiempo real, en caso de grandes desbalances generación - carga, el operador humano del SEP no tiene tiempo para realizar acciones de control manual, siendo los esquemas de protección por sobre/baja frecuencia los que actúan de forma automática. Normalmente, estos esquemas de protección tienen una parametrización única basada en valores de frecuencia mínima y tiempos de actuación definidos mediante estudios eléctricos fuera de línea [4].
El sistema de control p - f de los generadores es el encargado de mantener la frecuencia dentro de límites establecidos, ajustando automáticamente la potencia generada. Este sistema de control garantiza la estabilidad y la correcta operación del SEP en tiempo real [5], y su estudio ha ganado importancia con el crecimiento de los sistemas interconectados y la inclusión de las energías renovables no convencionales.
El comportamiento del sistema de control p - f, en la mayoría de los casos, se estudia mediante modelos de Respuesta de la Frecuencia del SEP ( SFR ), que se construyen integrando los dispositivos que realizan el control p - f de cada unidad de generación. En [6] se propone, por primera vez, usar modelos SFR reducidos para representar generadores térmicos y estudiar el comportamiento dinámico de la frecuencia; esta propuesta es, posteriormente, mejorada en [7] donde, usando modelos SFR reducidos de 1er orden, se propone un conjunto sencillo de ecuaciones para calcular directamente el nadir de la frecuencia y su tiempo de ocurrencia. Debido a la relevancia de los modelos SFR para el análisis de la estabilidad de frecuencia, se ha continuado con el desarrollo de modelos más completos que incluyen el efecto del Control Automático de Generación (AGC) [3], los Esquemas de Alivio de Carga (EAC) [4], modelación de parques eólicos [8] y centrales fotovoltaicas [9], e inclusive modelos SFR de los motores de inducción [10]. Es así que en [11] se propone un modelo SFR genérico de orden superior aplicable a diferentes tecnologías de generación y propone un procedimiento para estimar los parámetros del modelo, mientras que [12] propone estimar la respuesta del sistema usando una expresión analítica para aproximar la respuesta de los reguladores de velocidad de cada generador.
Conocida la relevancia de los modelos SFR, en el presente trabajo la metodología propuesta en [1] y [7] se aplica al Sistema Nacional Interconectado ecuatoriano para calcular el nadir de frecuencia y su tiempo de ocurrencia luego de un desbalance generación - carga. En este sentido, los modelos presentados en el trabajo se pueden emplear para: i) Parametrizar las protecciones por sobre y baja frecuencia, ii) Diseñar esquemas inteligentes de alivio de carga, iii) Realizar la sintonización del sistema de regulación de velocidad de generadores, etc. Los resultados del artículo contribuyen al desarrollo de las redes inteligentes, que pretenden que el SEP sea capaz de “autocurarse”, realizando acciones de control óptimas frente a cada disturbio que se presente en el sistema [13].
El artículo se estructura de la siguiente manera: en la Sección 2 se presentan los modelos SFR y una descripción de la metodología aplicada. Posteriormente, en la Sección 3 se aplica la metodología a un sistema de prueba académico, así como al Sistema Nacional Interconectado Ecuatoriano, donde se incluye un análisis para su aplicación en tiempo real. Se incluye también un análisis de sensibilidad relacionado con la cantidad de unidades de generación modeladas y su efecto en el valor estimado de la máxima desviación transitoria de la frecuencia. Finalmente, en la Sección 4, se resumen las principales conclusiones y recomendaciones del trabajo.
METODOLOGÍA
Modelos SFR
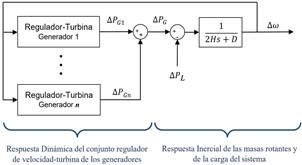
El modelo SFR permite calcular la respuesta dinámica de la frecuencia cuando ocurre un desequilibrio generación - carga y, usualmente, está compuesto por: turbina, regulador de velocidad, generador sincrónico y carga, tal como se muestra en la Fig. 1, donde el modelo regulador de velocidad - turbina debe ser reemplazado por el modelo que representa la tecnología particular de cada unidad de generación, por ejemplo: TGOV1, GAST y HYGOV, que representan a turbinas de vapor, gas e hidráulicas, respectivamente.
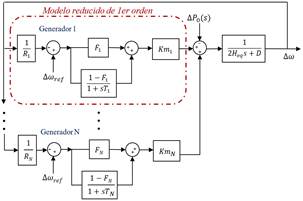
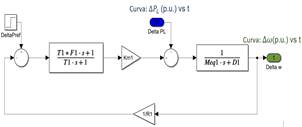
Para representar al conjunto regulador de velocidad - turbina se propuso en [6] un modelo reducido de 1er orden que, al incluirlo dentro del modelo SFR, se obtiene la respuesta promedio, colectiva y coherente de todos los generadores. Este modelo presenta una variedad de aplicaciones [14], [15], sin embargo, asume que los generadores que conforman el sistema son del tipo turbina de vapor. Por otra parte, en [7] se presenta un modelo reducido de 1er orden que admite una variedad de tecnologías para los reguladores de velocidad y turbinas. El modelo SFR equivalente para N generadores, se muestra la Fig. 2.
Considerando el modelo mostrado en la Fig. 2, la respuesta dinámica de la frecuencia ∆𝜔 𝑠 , frente a un desbalance generación - carga, en el dominio de Laplace está definida por [7]:
Donde, 𝐾𝑚 𝑖 , 𝐹 𝑖 , 𝑇 𝑖 y 𝑅 𝑖 son los parámetros del modelo reducido de 1er orden del i-esimo generador, determinados según el procedimiento descrito en la Sección 2.2, mientras que, 𝐻 𝑒𝑞 es la inercia equivalente del sistema y 𝐷 representa el amortiguamiento de la carga.
La inercia equivalente del sistema se calcula como la sumatoria del producto de la inercia 𝐻 𝑖 por la potencia nominal 𝑆 𝑖 de cada generador, dividida para la potencia base del sistema ?? 𝑠𝑦𝑠 , según la siguiente ecuación:
El desbalance generación - carga, representado por ∆ 𝑃 0 𝑠 , matemáticamente se modela mediante una función escalón unitario, que en el dominio de Laplace resulta ∆ 𝑃 0 𝑠 = ∆ 𝑃 0 𝑠 . Resolviendo la ecuación (1), la respuesta dinámica de la frecuencia en el dominio de Laplace y en el dominio del tiempo, está dada por:
Donde, 𝐴 𝑖 son los residuos reales o complejos y 𝑝 𝑖 son los polos reales o pares complejos conjugados de (1) [7].
Determinación de los Parámetros del Modelo Reducido de Primer Orden
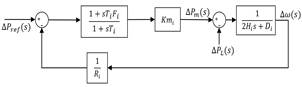
Durante un determinado período de tiempo, la respuesta dinámica del modelo reducido de 1er orden es muy similar a la respuesta del modelo completo del conjunto regulador de velocidad-turbina, independiente de la configuración de este. La Fig. 3 muestra el modelo reducido de 1er orden usado en la etapa de determinación de parámetros del modelo.
La función de transferencia del modelo reducido de 1er orden, ecuación (5), relaciona la velocidad del generador - salida del modelo ∆𝜔(𝑠) - con la variación de potencia debido a un desbalance - ∆𝑃 𝐿 𝑠 -, representada mediante un escalón unitario [1].
En el presente trabajo, la respuesta del modelo completo del generador, que incluye el modelo particular del conjunto regulador de velocidad-turbina, se obtiene mediante PowerFactory; mientras que la respuesta del modelo reducido de 1er orden se obtiene mediante Matlab. Empleando el Estimador de Parámetros de Simulink-Matlab [16], se logra que la respuesta del modelo reducido de 1er orden se ajuste a la respuesta del modelo completo (Curva 𝜔 vs 𝑡). Lo anterior se ilustra en la Fig. 4.
El ajuste se realiza considerando una ventana de tiempo que inicia cuando ocurre el desbalance generación - carga y finaliza cuando se alcanza el nadir de la frecuencia, este tiempo se obtiene de simulaciones previas en las que se estudia el comportamiento dinámico de la frecuencia. Los resultados que se obtengan del modelo equivalente de 1er orden solo serán válidos durante el periodo de tiempo de ajuste definido previamente [17].
Cálculo de la Máxima Variación Transitoria de la Frecuencia
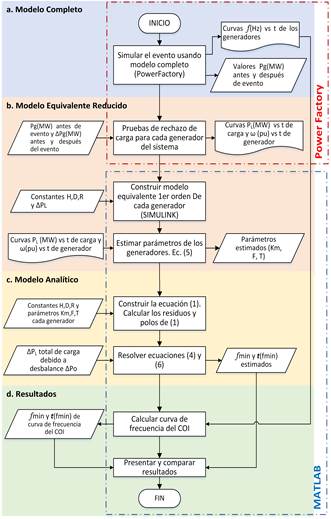
Para determinar el instante de tiempo 𝑡 𝑚𝑖𝑛 en el cual ocurre la máxima desviación transitoria de la frecuencia ∆ 𝑓 𝑚𝑖𝑛 , se debe resolver la ecuación (6), que resulta de derivar e igual a cero la ecuación (4).
Debe considerarse que (6) presenta un mínimo si la trayectoria de la frecuencia es sinusoidal amortiguada, es decir que (3) tiene, al menos, un par de polos complejos conjugados. Una vez determinado 𝑡 𝑚𝑖𝑛 , su valor se sustituye en (4) y se calcula ∆ 𝜔 𝑚𝑖𝑛 𝑡 𝑚𝑖𝑛 . Este valor multiplicado por la frecuencia nominal del sistema permite obtener la máxima desviación transitoria de la frecuencia ∆ 𝑓 𝑚𝑖𝑛 𝑡 𝑚𝑖𝑛 .
Proceso para Aplicación de la Metodología
En la Fig. 5 se presenta el diagrama de flujo de la metodología, donde se indican de forma secuencial los pasos a seguir para su aplicación a un sistema eléctrico de potencia.
APLICACIÓN Y RESULTADOS
Con el propósito de presentar de forma didáctica la metodología, en primera instancia se aplica al sistema IEEE New England de 39 barras y 10 generadores. Posteriormente, se aplica al Sistema Nacional Interconectado ecuatoriano ( SNI ) considerando los escenarios hidrológicos lluvioso y seco, que presentan distintos patrones en el despacho de las unidades de generación.
Sistema IEEE New England
3.1.1 Respuesta del Modelo Completo
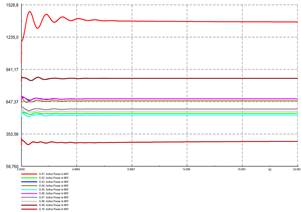
El sistema se modela en PowerFactory, donde los parámetros de cada generador se ingresan considerando como potencia base la potencia activa nominal de cada generador. El modelo incluye reguladores de voltaje (IEEET1) y de velocidad (TGOV1 para centrales térmicas y HYGOV para centrales hidráulicas). Se simula un aumento de carga del 10% de la potencia activa total, a los 0 s. El comportamiento de la frecuencia y potencia activa generada se presenta a continuación:
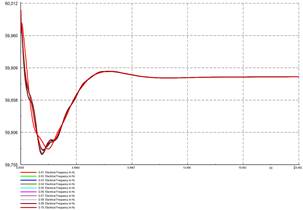
En la Fig. 6 se aprecia la caída de la frecuencia en todas las barras del sistema debido al aumento de la carga, mientras que la Fig. 7 ilustra el aumento de potencia activa generada producto de la actuación del sistema de control p - f de los generadores. En ambas figuras se observa que la frecuencia y la potencia activa generada se estabilizan luego de aproximadamente 20 s de ocurrido el evento. Para determinar la variación de potencia activa generada por cada unidad debido al desbalance ∆𝑃 𝐿 (𝑠), se registran los valores previos al evento, y, a los 20 s. Mediante una función escalón unitario se aproxima el comportamiento de la potencia activa generada por cada generador, de tal modo que se pueda usar en las siguientes etapas de la metodología.
3.1.2 Modelo Equivalente Reducido
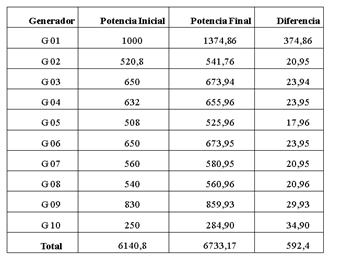
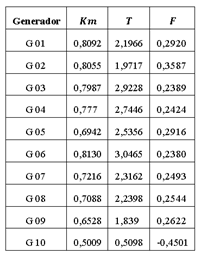
Se simulan pruebas de rechazo de carga con el propósito de obtener las curvas velocidad (p.u) vs tiempo de cada generador, operando de forma aislada. Dicha prueba se realiza con la función “Step Response Test” de PowerFactory; la carga base corresponde a la potencia activa generada antes del evento, y el valor de carga adicional ∆ 𝑃 𝐿 se obtiene de la diferencia entre el valor de potencia activa generada a los 20 s y el valor de potencia activa generada previo al disturbio. Esta diferencia de potencia será el módulo de la función escalón unitario que ingresa al modelo equivalente reducido del generador (Ver Tabla 1).
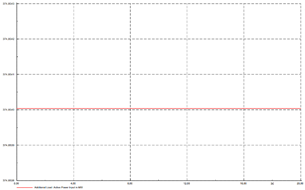
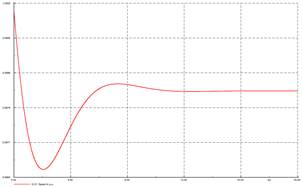
Como resultado de la prueba de rechazo de carga se obtienen las curvas (escalón unitario) de potencia activa de carga (MW) vs tiempo, y, de velocidad (p.u.) vs tiempo de los generadores. A continuación, se presentan las curvas obtenidas de las pruebas de rechazo de carga del generador G01.
Las curvas son exportadas al “Estimador de Parámetros” de Simulink-Matlab con el fin de obtener los parámetros del modelo reducido de 1er orden. La implementación en Simulink se muestra en la Fig. 10, donde como entrada se tiene la curva ∆ 𝑃 ?? 𝑝𝑢 𝑣𝑠 𝑡, obtenida de PowerFactory y corresponde a la carga adicional, expresada en p.u considerando como potencia base la potencia activa nominal del generador; como salida se tiene la curva ∆𝜔 𝑝𝑢 𝑣𝑠 𝑡, también obtenida de PowerFactory.
En el modelo reducido de 1er orden se ingresan las constantes del generador ( 𝐻 𝑖 ), ( 𝐷 𝑖 ) y el estatismo permanente del regulador de velocidad ( 𝑅 𝑖 ), que se asumen conocidas. ∆𝑃 𝑟𝑒𝑓 es una función escalón unitario que, para el presente estudio, se considera constante e igual a cero, ya que el modelo no considera la Regulación Secundaria de frecuencia ( RSF ) y, 𝑀 𝑒𝑞 es el momento de inercia del generador.
Aplicado el “Estimador de Parámetros” se obtienen los parámetros del modelo reducido de 1er orden de los generadores del sistema, mostrados en la Tabla 2.
3.1.3 Modelo Analítico
En primera instancia, es necesario definir la potencia base del sistema, para proceder a expresar los valores de 𝐻 𝑒𝑞 , 𝐷 𝑒𝑞 y 𝑅 𝑖 en esta nueva base. Estas constantes, aplicando el cambio de base, se determinan mediante:
Donde:
Se eligió la potencia base del sistema 𝑃 𝑠𝑠𝑠 =100 MVA, mientras que la variación total de potencia provocada por el desbalance ∆𝑃 0 (pu sobre la base del sistema) se calcula como:
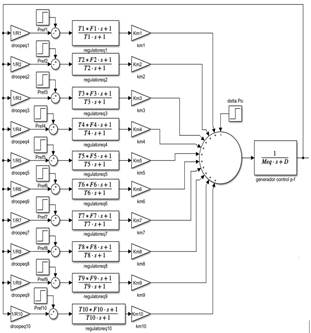
El modelo SFR del sistema IEEE New England, empleado un modelo equivalente reducido de 1er orden para representar el control p - f de los generadores, queda representado como se muestra en la Fig. 11.
Para encontrar los polos y residuos de la ecuación (1), es necesario reemplazar las constantes calculadas y los parámetros de cada generador. Los residuos y polos calculados se substituyen en (6), así como la variación total de potencia provocada por el desbalance ∆𝑃 0 , y se procede a calcular el instante en el que sucede la máxima desviación de frecuencia. El resultado obtenido para el sistema IEEE New England es 𝑡=2,1357 𝑠. Finalmente, el valor de 𝑡 se reemplaza en (4) y se obtiene ∆𝜔 𝑚𝑎𝑥 en p.u, que corresponde a ∆𝑓 min =−0,332 Hz, es decir, el nadir de la frecuencia es 𝑓 min =59,776 Hz.
3.1.4 Comparación con Modelo Completo
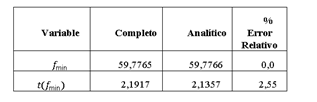
Para propósito de comparación se calcula la frecuencia del Centro de Inercia ( COI ) del sistema usando la velocidad de los generadores, obtenida de la simulación en PowerFactory del modelo completo. Se determina que la frecuencia mínima alcanzada es 59,776 Hz, y que ocurre a los 2,1917 s.
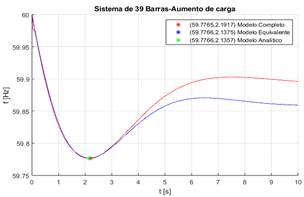
En la Fig. 12 se presentan: i) La frecuencia del COI (Modelo Completo), ii) La frecuencia obtenida del modelo equivalente reducido, y iii) El valor de la máxima variación transitoria de la frecuencia y tiempo de ocurrencia calculadas mediante el modelo analítico.
En la Tabla 3 se aprecia que el resultado, en cuanto a frecuencia, del modelo analítico es igual al obtenido mediante el modelo completo. Mientras que, el instante de tiempo en el que ocurre la máxima variación transitoria de la frecuencia, presenta una ligera diferencia, es decir un error relativo del 2,55%.
Sistema Nacional Interconectado Ecuatoriano (SNI)
Se consideran dos casos de estudio: i) Demanda máxima en estación hidrológica lluviosa, con predominio de generación hidráulica, y, ii) Demanda máxima en estación seca, donde la generación térmica aumenta. Para el escenario lluvioso se considera el despacho de generación del día 13 de marzo del 2019 a las 19:30, mientras que para el escenario seco se considera el despacho de generación del día 24 de octubre del 2018, a las 19:30. El modelo eléctrico de la red y los modelos dinámicos de los generadores son proporcionados por el Operador Nacional de Electricidad (CENACE). El sistema colombiano, para el escenario seco, está representado por un generador equivalente [18], y para el escenario lluvioso se representa como una carga equivalente. El modelo completo resultante se simula empleando PowerFactory.
3.2.1 Selección de Unidades de Generación
Los casos de estudio contienen: 110 unidades de generación activas en el escenario lluvioso, y, 117 unidades de generación activas en el escenario seco, lo que significa estructurar un modelo equivalente reducido complejo, de gran tamaño y, posiblemente, de alto tiempo de cálculo. Por estas razones, resulta conveniente elegir un conjunto reducido de generadores que representen el comportamiento del sistema.
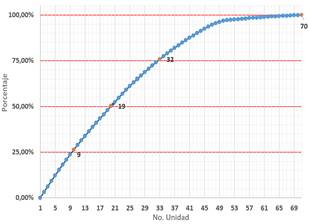
Debido a que el modelo no incluye la Regulación Secundaria de Frecuencia, se considera que ∆𝑃 𝑟𝑒𝑓 =0, por tanto, considera solamente la respuesta inercial y la Regulación Primaria de Frecuencia ( RPF ) frente a un desbalance generación - carga. Para seleccionar los generadores que deben incluirse en el modelo se emplea la información del aporte promedio a la RPF de cada generador obtenida de [19], donde se indica que el número de unidades que participan en RPF es setenta. Se determina el aporte promedio acumulado a la RPF, calculado como la suma de la potencia promedio que aporta cada generador que participa en la RPF, y que se presentada en la Fig. 13.
Se observa que, aproximadamente, el 75% de aporte promedio a la RPF corresponde los 32 primeros generadores que más aportan a la RPF. En los últimos deciles se observa que el aporte de los generadores es muy bajo, y podría no ser necesario incluir dichos generadores en el modelo equivalente reducido.
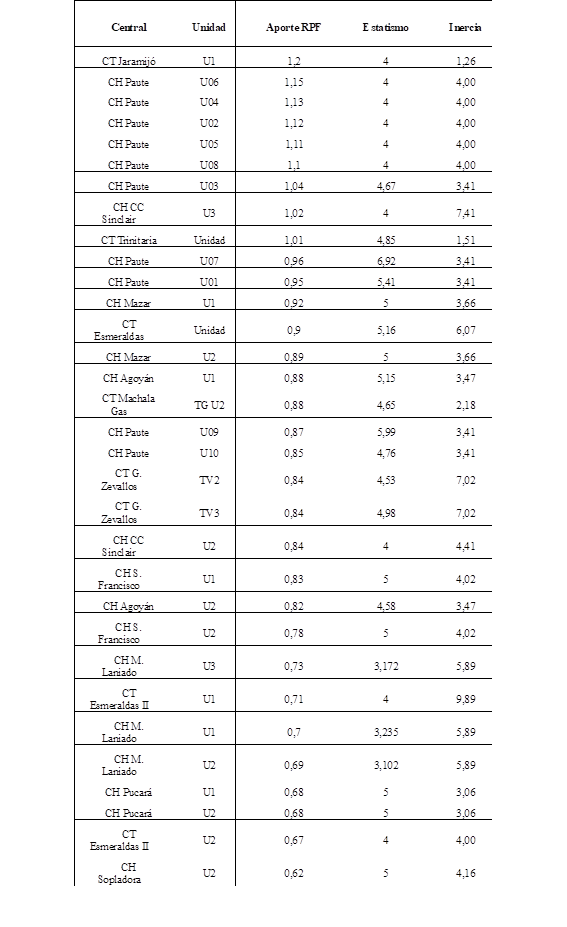
Mediante un análisis de sensibilidad se determina que, al incluir en el modelo equivalente reducido los generadores que corresponden al 75% de aporte promedio acumulado a la RPF, se obtiene el menor error relativo en la máxima desviación transitoria de la frecuencia y su tiempo de ocurrencia, considerando como referencia el modelo completo simulado en PowerFactory. En la Tabla 4 se listan los generadores considerados, así como sus características técnicas estatismo e inercia, relevantes para el estudio.
3.2.2 Caso 1: Demanda Máxima - Escenario Seco
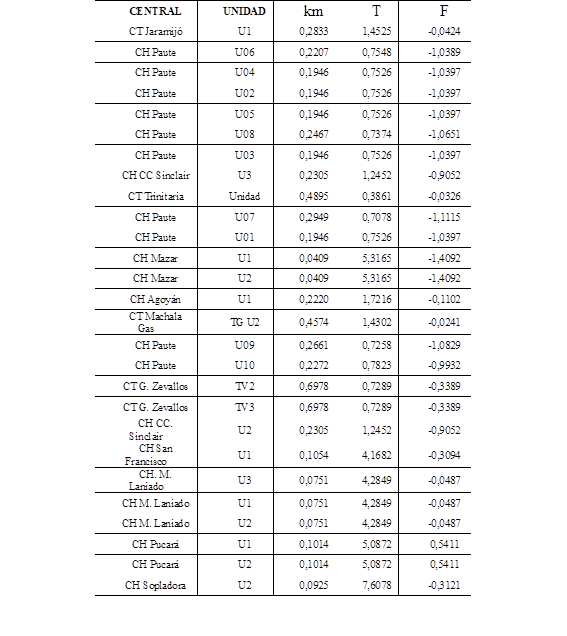
Para el escenario seco, el evento simulado es la salida de la línea de transmisión ( L/T ) Pomasqui - Jamondino 230 kV (Interconexión Ecuador - Colombia), a los 0 s. La salida de la L/T representa una pérdida de generación en el sistema ecuatoriano, con la consiguiente caída de la frecuencia. En la simulación del modelo equivalente reducido y modelo analítico se utilizan los parámetros presentados en la Tabla I del Anexo.
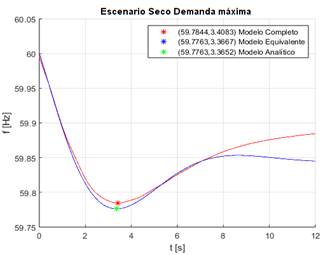
En la Fig. 14 se presentan: i) La frecuencia del COI (Modelo Completo), ii) La frecuencia obtenida del modelo equivalente reducido, y iii) El valor de la máxima variación transitoria de la frecuencia y tiempo de ocurrencia, calculadas mediante el modelo analítico.
Los resultados más importantes del caso de estudio se presentan tabulados en la Tabla 5.
3.2.3 Caso 2: Demanda Máxima - Escenario Lluvioso
En el escenario lluvioso se simula la salida, a los 0 s, de la Interconexión Ecuador - Colombia a 230 kV. En este caso, la salida de la línea de interconexión implica pérdida de carga en el sistema ecuatoriano, con el consiguiente aumento de la frecuencia.
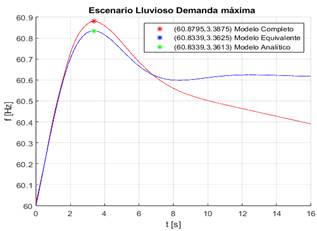
En la Fig. 15 se presentan: i) La frecuencia del COI (Modelo Completo), ii) La frecuencia obtenida del modelo equivalente reducido, y iii) El valor de la máxima variación transitoria de la frecuencia y tiempo de ocurrencia calculadas mediante el modelo analítico.
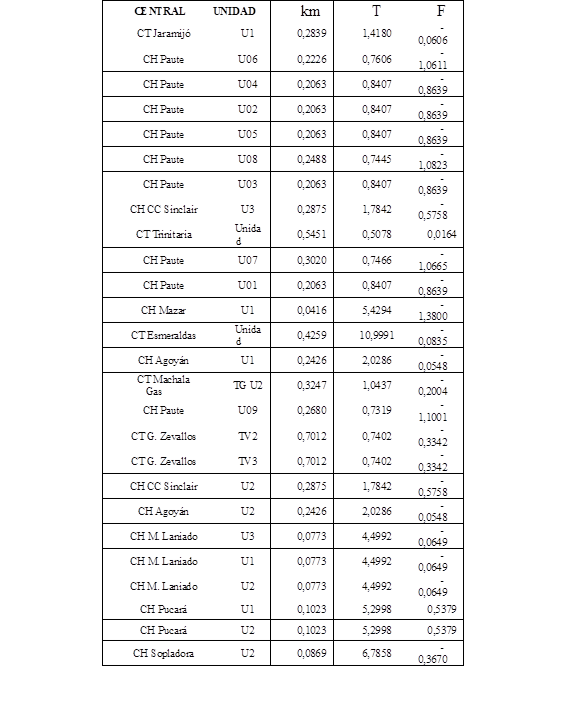
Para realizar las simulaciones, se utilizan los parámetros presentados en la Tabla II del Anexo. Los resultados más importantes se presentan tabulados en la Tabla 6.
3.2.4 Análisis de Resultados
De los resultados obtenidos se observa que la máxima desviación transitoria de la frecuencia, obtenida del modelo analítico, presenta un error menor a 0,1% respecto del valor obtenido de la curva de frecuencia del COI (modelo completo). Por otra parte, el tiempo en que ocurre la máxima desviación transitoria de la frecuencia, calculado mediante el modelo analítico, presenta un error menor al 2 % respecto del valor obtenido del modelo completo. Se concluye que la metodología propuesta estima con alta precisión la máxima variación transitoria de la frecuencia y su tiempo de ocurrencia, donde el mayor error se presenta en la variable del tiempo, independientemente del caso de estudio.
Los valores estimados de los parámetros del modelo de primero orden, para ambos casos de estudio, son muy similares (ver Tablas I y II del Anexo). En los casos en que los parámetros ( 𝐾𝑚 𝑖 , 𝐹 𝑖 , 𝑇 𝑖 ) son diferentes, ésta diferencia se ve reflejada en el tiempo de ocurrencia de la máxima desviación de frecuencia, donde los errores relativos difieren en 0,793%; es decir, el impacto de los parámetros estimados no es significativo.
Para el SNI, el grupo de generadores que conforman el modelo equivalente reducido de 1er orden consta de 32 unidades. Estas unidades representan el 75 % del aporte promedio de la RPF total y, al ser incluidas en el modelo analítico, entregan resultados cercanos a los resultados obtenidos mediante el modelo completo.
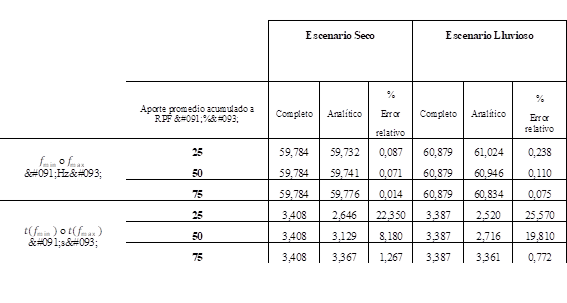
Un análisis de sensibilidad, mostrado en la Tabla 7, muestra que el error aumenta cuando el número las unidades incluidas en el modelo disminuye.
El modelo analítico fue implementado en Matlab y demora menos de 2,0 s en calcular la máxima desviación transitoria de la frecuencia y su tiempo de ocurrencia, considerando un sistema equivalente reducido con 32 unidades. La comparación de los tiempos de cálculo (simulación) de cada modelo, hasta llegar al punto en que ocurre la máxima desviación transitoria de la frecuencia, se muestra en la Tabla 8.
CONCLUSIONES Y RECOMENDACIONES
El modelo equivalente reducido permite determinar el comportamiento dinámico de la frecuencia con alta exactitud. La máxima desviación transitoria de la frecuencia obtenida del modelo analítico es muy cercana a la respuesta dinámica obtenida mediante PowerFactory que modela con alto detalle el control p - f de los generadores, así como respuesta de la red y de la carga.
Los parámetros estimados del modelo reducido de 1er orden de los generadores pueden ser empleados para estimar la respuesta de la frecuencia en distintos escenarios operativos, es decir la estimación debe realizarse una sola vez, por cada generador. Sin embargo, la mayor cantidad de trabajo de la metodología se concentra en el proceso de determinación del modelo reducido de 1er orden de cada generador (estimación de parámetros).
El tiempo de cálculo cuando se usa el modelo analítico es muy bajo, lo que significa que el modelo podría aplicarse a la operación en línea, inclusive en tiempo real. En el caso SNI, el instante de tiempo en que se alcanza el nadir de la frecuencia fue 3,4 s y tomó alrededor de 1,9 s estimar dicho valor. Además, los tiempos de cálculo pueden ser menores si se implementa la metodología usando lenguajes de programación de alto rendimiento.
Cabe indicar que los modelos SFR son aplicables para analizar la dinámica promedio del sistema, en ese sentido no reflejan las oscilaciones entre generadores que puedan presentarse. Por otro lado, los modelos SFR convencionales no consideran las no linealidades asociadas con la posición y límites técnicos de las válvulas o compuertas del sistema de regulación de velocidad - turbina. Esta ha sido una limitación en el trabajo actual, que debe ser abordada en trabajos futuros, especialmente en el SNI, donde muchos generadores se despachan a su potencia nominal.
Finalmente, el aporte principal del presente artículo es presentar los modelos SFR reducidos de primer orden de las principales unidades de generación del SNI, que hasta donde los autores conocen, no se ha realizado/presentando antes. Estos modelos pueden ser empleados para el estudio y mejora de la estabilidad de frecuencia del sistema eléctrico ecuatoriano.