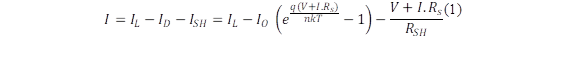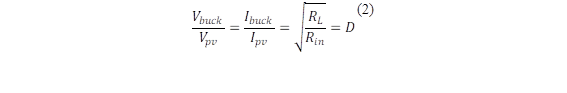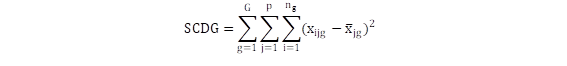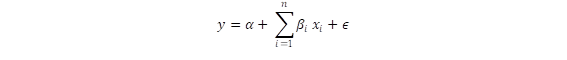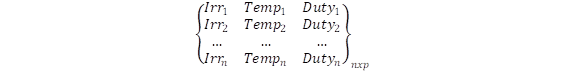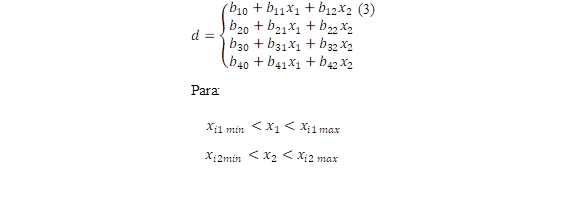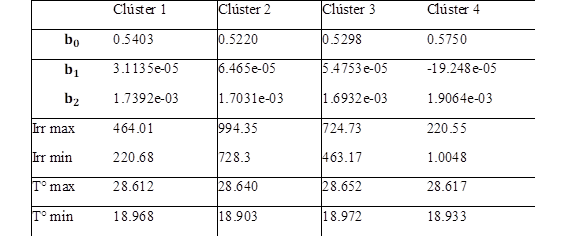INTRODUCCIÓN
La creciente demanda energética, junto con la imperativa necesidad de mitigar las emisiones de dióxido de carbono (CO2), ha conferido prioridad a la incorporación de fuentes de energía renovable en el sistema eléctrico. La integración de modalidades como la generación eólica, solar e hidráulica se erige como una estrategia fundamental para promover una matriz energética más ecológica y sostenible [1].
Debido al avance de la tecnología y al uso de diferentes tipos de energía, se ha determinado que la energía eléctrica producida por paneles fotovoltaicos es una de las más valiosas y eficaces, además esta energía se vuelve popular debido a su bajo costo de mantenimiento y operación. [2]
Sin embargo, la integración de estas energías conlleva una serie de grandes retos desde el punto de funcionamiento fiable y control. En [3] se hace un repaso de las estrategias de control en microrredes y se revisan las tendencias de control más avanzadas a partir de principios de control como el control de estatismo, control predictivo de modelos, sistemas multi-agente entre otros.
Teniendo en cuenta las propiedades físicas de los semiconductores de las células solares y su comportamiento no lineal [4], la máxima potencia posible se encuentra en el pico de la curva potencia- voltaje, un pobre control para encontrar este punto de operación en los paneles fotovoltaicos causa un bajo rendimiento en la producción de energía solar siendo esta del 13.1% al 24.4% de la capacidad total. [5]
La intermitencia natural del recurso primario tanto en irradiación y temperatura, afectan la capacidad de producción de los sistemas fotovoltaicos, ya que las curvas de voltaje - corriente de las celdas se ven afectadas como se muestra en el modelo matemático presentado en [6], en este sentido se han desarrollado algoritmos seguidores de máxima potencia, que consisten en controlar el ciclo de trabajo de un conversor DC-DC.
Se han empleado diferentes metodologías tradicionales para el control del ciclo de trabajo como son: Perturba y observa, conductancia incremental, método de ajuste de curvas, métodos con lógica difusa y redes neuronales [7] Estas metodologías buscan maximizar la potencia entregada por los paneles solares adaptando continuamente las condiciones de operación para rastrear el punto de máxima potencia, variando la carga o el ciclo de trabajo del conversor DC-DC, sin embargo, estos métodos presentan desventajas frente a condiciones de rápida variación del recurso, ya sea en la eficiencia del panel o en el error de seguimiento de máxima potencia, debido al tiempo de procesamiento, el aporte significativo de este trabajo que utiliza regresión lineal radica en la introducción de una técnica adicional y específica: el empleo de regresión lineal para mejorar el control del ciclo de trabajo en sistemas fotovoltaicos. Este enfoque puede ofrecer ciertas ventajas, como una implementación más sencilla en comparación con algunas técnicas más complejas como las redes neuronales, una menor carga computacional o un comportamiento más predecible. En [7] se desarrolla el algoritmo de control, basado en un regresor lineal considerando como variable independiente el voltaje y la corriente para predecir el ciclo de trabajo, este control ha presentado resultados satisfactorios frente a algoritmos como: perturba y observa (P&O), Optimización de enjambre de partículas (PSO), Algoritmo de polinización de flores (FPA). Sin embargo, esta metodología presenta ciertas debilidades como: despreciar la variabilidad del recurso, y los fallos del regresor frente al comportamiento no lineal.
Con estos antecedentes en el presente artículo se plantea la implementación de un regresor lineal multivariante, a partir de un análisis de conglomerados que permitirá el ajuste más preciso de las regresiones, la implementación es verificada en una topología con una barra infinita y en operación dentro de una microrred conformada por otras fuentes de energía renovable y generadores convencionales.
Dada las ventajas y aplicaciones que presentan las nuevas técnicas de simulación expuestas [8], se realiza el entrenamiento del regresor en Matlab/Simulink versión 2022b, y la implementación del modelo y pruebas dentro del sistema eléctrico en el software de análisis de transitorios electromagnéticos HYPERSIM, mismo que nos permite analizar los valores instantáneos trifásicos de las variables eléctricas y de control del sistema.
El presente trabajo se estructura en varias secciones para abordar de manera integral el desarrollo y la implementación de una metodología de seguimiento del punto de máxima potencia (MPPT) en sistemas fotovoltaicos, la Sección 2 se enfoca en el funcionamiento de los paneles fotovoltaicos, su modelado, el algoritmo MPPT y conceptos como clustering y regresión lineal. La Sección 3 describe la metodología propuesta para entrenar los regresores y su implementación en una red de prueba, con resultados presentados en la Sección 4, evaluando escenarios de conexión a la red (Barra infinita) y a la microrred. La Sección 4 profundiza en el diseño, simulación y gráficas generadas por el algoritmo de MPPT implementado en Hypersim. Finalmente, la Sección 5 ofrece conclusiones derivadas de los resultados obtenidos junto con recomendaciones. Esta estructura exhaustiva y detallada del trabajo permite una comprensión completa del desarrollo, aplicación y evaluación de la metodología propuesta para mejorar el seguimiento del punto de máxima potencia en sistemas fotovoltaicos.
VISIÓN GENERAL DE UN SISTEMA FOTOVOLTAICO
Un sistema fotovoltaico se compone principalmente de paneles solares, seguidores MPPT, controladores y convertidores electrónicos de potencia y la carga [9]. Bajo este criterio, el modelamiento de este sistema se puede dividir en los siguientes componentes:
Panel Fotovoltaico (PV)
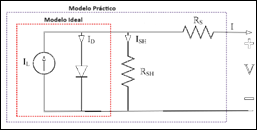
El modelo de diodo único de célula solar se muestra en la Fig. 1.
Un conjunto de células solares interconectadas conforma un panel fotovoltaico, las conexiones entre estos distintos módulos puede realizarse en serie o en paralelo. La relación entre el voltaje y la corriente de una célula solar viene definida por [9]:
Donde:
El voltaje de salida está determinado por la corriente de salida generada, misma que depende principalmente de las condiciones de radiación solar y temperatura. La corriente de salida es directamente proporcional a la irradiancia. Por lo tanto, cuando existen diferentes condiciones de irradiancia habrá diferentes puntos de salida en los paneles fotovoltaicos, lo que da lugar a la necesidad de contar con un control que regule el punto de funcionamiento en base a las variables de irradiación y temperatura [10].
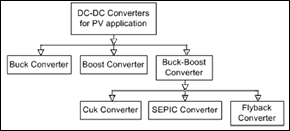
Convertidores de potencia DC-DC
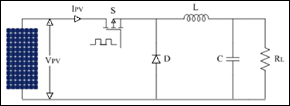
En un sistema fotovoltaico, los convertidores de potencia DC-DC se utilizan para cambiar el voltaje de salida de un nivel a otro, el convertidor permite extraer la potencia disponible en el panel e inyectarla a la carga, los convertidores se pueden clasificar según su aplicación en convertidor Boost, Buck, Buck-Boost, etc. El convertidor DC-DC es el medio por el cual el control MPPT realiza el cambio de nivel de voltaje en función de la corriente de salida para el seguimiento del punto de máxima transferencia de potencia. En la Fig. 2 se presenta de forma resumida los convertidores usados en el sistema fotovoltaico [11]:
Dentro del presente trabajo, se optará por la implementación de un convertidor DC-DC tipo Buck debido a sus ventajas significativas y sus modos de operación versátiles, lo que lo convierte en una elección óptima para la aplicación propuesta [8]. Este tipo de convertidor es reconocido por su eficiencia en la reducción de la tensión de entrada a niveles más bajos, su capacidad para regular la tensión de salida y su amplia utilización en sistemas fotovoltaicos para maximizar la eficiencia de conversión de energía solar a eléctrica. Además, su diseño simplificado y su capacidad para trabajar con una variedad de cargas lo hacen altamente adecuado para el propósito de este trabajo.
Convertidor Buck
El modo de operación de este tipo de convertidor ya sea de conducción continua o discontinua, depende del estado del switch y del diodo. La relación de conversión del voltaje se define por [11] :
Donde:
Los convertidores Buck sirven para regular el voltaje, corriente y potencia del panel fotovoltaico, el modo de funcionamiento del convertidor cambia en función de la variación de las condiciones climáticas debido al cambio de la irradiancia y la temperatura, la configuración del convertidor se modifica conforme se detalle en [12].
El diagrama de un convertidor Buck se ilustra en la Fig. 3:
Controladores de seguimiento del punto de máxima potencia (MPPT)
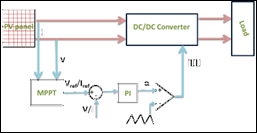
El control MPPT actúa sobre la electrónica de potencia de los conversores DC-DC o del inversor de los paneles fotovoltaicos con el fin de permitir la extracción de la mayor energía posible y está basado en algunos algoritmos que dan como respuesta la modulación por ancho de pulso (PWM por sus siglas en ingles “Pulse Width Modulation”) que ingresa a los convertidores.
A lo largo de los años, se han propuesto numerosos algoritmos MPPT, los cuales difieren en cuanto a eficiencia, velocidad de seguimiento, oscilaciones en estado estacionario, complejidad en la implementación de hardware. Además, cada método puede funcionar eficazmente en determinadas ocasiones y en otras no [14]. Por ejemplo, algunos métodos MPPT ofrecen un rendimiento más alto cuando la irradiancia permanece estable, por el contrario, otros algoritmos tienen resultados más satisfactorios cunado existe un cambio rápido de irradiancia.
El control MPPT más común está basado en la corriente o el voltaje el algoritmo permite la búsqueda de estas dos variables de acuerdo con una referencia y calcula el error, este error es utilizado por un regulador proporcional integrador, conocido por sus siglas en inglés (PI) para determinar el ancho de pulso (ciclo de trabajo) que obliga al convertidor a extraer el MPP del PV. En la Fig. 4 se muestra el esquema general del control MPPT en un sistema fotovoltaico.
Los distintos enfoques utilizados para el MPPT pueden clasificarse según las técnicas utilizadas, características del PV o métodos enfocados en optimización mediante computación.
Técnica directa de Perturbar y Observar (P&O)
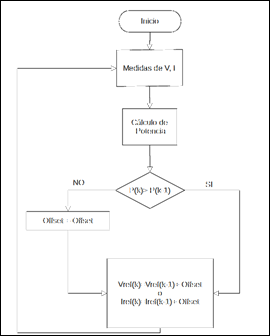
Con la finalidad de entender el objetivo de un algoritmo MPPT se presenta el principio de funcionamiento de la técnica (P&O) en el diagrama de flujo de la Fig. 5.
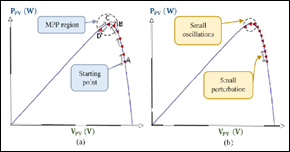
En esta estrategia, se emplea un paso fijo para calcular una señal objetivo en un lazo de control proporcional integral (PI), la señal de perturbación puede ser el voltaje de referencia o la corriente fotovoltaica La Fig. 6 (a) presenta la variación de la potencia operativa en el controlador de seguimiento del punto de máxima potencia (MPPT). Iniciando desde el punto A, la potencia operativa aumenta progresivamente con un valor constante de 'offset'. Cuando el punto operativo alcanza el punto D, el método P&O detecta una disminución en la potencia del panel, ajustando la pendiente del 'offset' y aumentando el voltaje de referencia de D a C para compensar la pérdida de energía fotovoltaica. Sin embargo, debido a la dirección constante del 'offset', el voltaje de referencia sigue aumentando hasta que se detecta una disminución de potencia en el punto B. Nuevamente, el valor de referencia se ajusta según el 'offset'. Por ende, de acuerdo con la naturaleza del método P&O previamente descrita, la potencia operativa oscilará continuamente entre los puntos D y B. El paso de perturbación 'offset' se elige generalmente por el diseñador del sistema mediante un enfoque de prueba y error. Por lo tanto, la solución ofrecida por este método es específica del sistema y no general.
Análisis de Conglomerados (Clustering)
El análisis de conglomerados es un método de clasificación automática no supervisada, que tiene la finalidad de agrupar elementos homogéneos considerando las similitudes que existen. Este análisis busca solventar los siguientes problemas [15]:
Cada elemento debe pertenecer a un único grupo.
Todos los elementos deben ser clasificados.
Cada grupo debe ser homogéneo.
Existen varios métodos de clusterización, entre ellos: K-means, Método de mapas auto organizados de Kohonen (SOM), K-medoids, Distancia de deformación dinámica del tiempo medida(DTW). De ellos se va a usar K-means que muestra un mejor funcionamiento. [16]
Existen varios métodos de clusterización, entre ellos: K-means, Método de mapas auto organizados de Kohonen (SOM), K-medoids, Distancia de deformación dinámica del tiempo medida(DTW). De ellos se va a usar K-means que muestra un mejor funcionamiento [6].
El algoritmo de k-means minimiza la suma de los cuadrados dentro de los grupos.
Donde:
Regresor Lineal
La predicción de valores continuos se puede modelar mediante una técnica estadística llamada regresión. El objetivo del análisis de regresión es determinar el mejor modelo que pueda relacionar la variable de salida con varias variables de entrada [17].
La relación que se ajusta a un conjunto de datos se caracteriza por un modelo de predicción llamado ecuación de regresión. La forma más utilizada del modelo de regresión es el modelo lineal general escrito formalmente como:
Donde:
Entre las ventajas, destaca su simplicidad interpretativa, ya que proporciona ecuaciones lineales fáciles de comprender, facilitando la comunicación de resultados, permite un procesamiento rápido de grandes conjuntos de datos. La identificación de relaciones lineales es otra fortaleza, especialmente cuando se presume una tendencia lineal entre la variable dependiente y las independientes. Por otro lado, la regresión lineal también enfrenta desventajas. Su sensibilidad a valores atípicos puede distorsionar los resultados y afectar la precisión del modelo. La asunción de linealidad puede ser una limitación cuando la relación real entre las variables es más compleja [7].
Monte Carlo
La simulación Monte Carlo se fundamenta en la realización de muestreos aleatorios repetidos y análisis estadísticos para calcular los resultados. Este método de simulación guarda estrecha relación con los experimentos aleatorios, donde el resultado específico no es conocido de antemano. En este contexto, la simulación Monte Carlo puede entenderse como un enfoque sistemático para llevar a cabo análisis hipotéticos. Tiene el siguiente método:
Generación de Muestras Aleatorias: Se utiliza la generación de muestras aleatorias para representar la variabilidad inherente a un problema estadístico. Estas muestras se obtienen de distribuciones de probabilidad que modelan las incertidumbres en los datos o parámetros del problema.
Simulación del Fenómeno: Utilizando las muestras aleatorias generadas, se lleva a cabo una simulación del fenómeno de interés. Esto implica aplicar el modelo estadístico o matemático a cada muestra y observar los resultados obtenidos.
Estimación de Resultados: A través de la repetición de la simulación con un gran número de muestras, se obtiene una distribución de los resultados. La media y la varianza de esta distribución proporcionan estimaciones puntuales y medidas de la incertidumbre asociada con la cantidad que se está evaluando.
Aplicaciones en Inferencia Estadística: El método de Monte Carlo se emplea de manera destacada en inferencia estadística, especialmente en el enfoque bayesiano. Técnicas como el Markov Chain Monte Carlo (MCMC) posibilitan la exploración eficiente de distribuciones de probabilidad a posteriori, facilitando la estimación de parámetros y respaldando la toma de decisiones basada en la incertidumbre. [8]
Inversor con control PWM
El PWM, es una técnica utilizada en inversores para regular la magnitud del voltaje y la frecuencia en sistemas de corriente alterna trifásica. Esta técnica consiste en variar el ancho de los pulsos de una señal de voltaje modulada, manteniendo constante la frecuencia, para controlar la potencia suministrada a la carga. En el contexto de un inversor, el PWM opera generando una señal de voltaje alterna sintética a partir de una fuente de voltaje continua. El ancho de los pulsos en esta señal se ajusta de acuerdo con la magnitud del voltaje y la frecuencia requerida en el punto de conexión común (PCC) de la red trifásica. Este control preciso del ancho de los pulsos permite regular el voltaje y la frecuencia de salida del inversor para que coincidan con los parámetros necesarios por la red eléctrica. En cuanto a la aplicación en el modelo, en un software de simulación como MATLAB/Simulink, se implementó el control PWM mediante bloques específicos que simulan la generación de pulsos y su modulación para obtener la forma de onda deseada de salida. Estos bloques permitirían ajustar el ancho de los pulsos de acuerdo con las consignas de voltaje y frecuencia requeridas en el punto de conexión común, reproduciendo así el comportamiento real del inversor con control PWM en la simulación del sistema eléctrico, la especificaciones y composición del inversor con control PWM se detallan en [18].
METODOLOGIA PROPUESTA
La metodología propuesta consiste en la interacción de tres etapas principales: formación de la red equivalente, generación de escenarios operativos en los cuales la irradiancia es mayor a 100 W/m2 y minería de datos.
Caracterización del Sistema Fotovoltaico
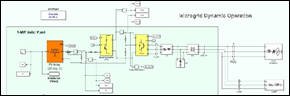
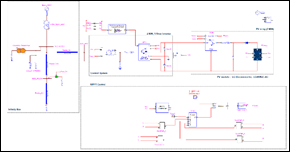
El desarrollo de la presente metodología se aplica a un sistema fotovoltaico incorporado en una microrred, con una disposición en la que el panel solar forma parte de una red eléctrica de escala local, características que se detallan en la Tabla 1 y se observa en la Figura 7.
Tabla 1: Características del Sistema Fotovoltaico
| Módulos Paralelo | 540 |
| Módulos en Serie | 10 |
| Número de celdas por módulo | 83 |
| Voltaje de circuito abierto | 51.9 [V] |
| Corriente de corto circuito | 8.68 [A] |
| Voltaje en el punto de máxima potencia | 40.0 [V] |
| Corriente en el punto de máxima potencia por modulo | 8.00 [A] |
Simulación de Monte Carlo
La simulación de Monte Carlo (SMC) se basa en experimentos aleatorios para llevar a cabo un análisis estadístico de los resultados. Los modelos matemáticos dependen de una cierta cantidad de datos de entrada para obtener una o varias salidas. Es común someter a los modelos a escenarios específicos, como el mejor y el peor caso. Sin embargo, este enfoque no es apropiado, ya que no considera el riesgo asociado a la variación de las diferentes variables de entrada. Por otro lado, al considerar un número excesivamente grande de eventos posibles, se dificulta la toma de decisiones y la capacidad de almacenamiento del comportamiento del modelo [19].
En la simulación de Monte Carlo se realiza un análisis de la distribución estadística necesaria para usar como fuente de generación de datos de entrada, de la cual se extraen ciertos valores como entradas al modelo [19].
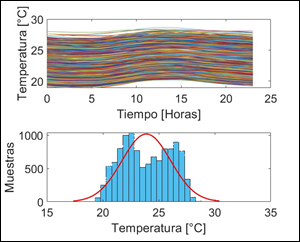
Con la finalidad de encontrar las características para la implementación del algoritmo de Monte Carlo, se realiza un análisis estadístico del comportamiento de recurso primario.
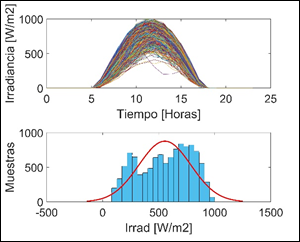
Con ayuda de la herramienta Web (Data Access Viewer - NASA POWER) de la NASA (National Aeronautics and Space Administration). En las Fig. 7 y Fig. 8 se muestra la variabilidad del recurso primario en un periodo de 3 años de una zona específica.
De los datos obtenidos se puede extraer las características de las variables de entrada para la simulación de Monte Carlo.
Tabla 2: Estadísticos del Recurso Primario
| Componente | Variable | Características |
| Sistema Fotovoltaico | Irradiancia [W/m2] | Media: 555.18 Desviación estándar: 232.36 |
| Sistema Fotovoltaico | Temperatura [°C] | Media: 23.56 Desviación estándar: 2.2131 |
Se implementa la red equivalente en Simulink de Matlab de la Fig. 7 para realizar la SMC, con los datos obtenidos del análisis estadístico del recurso primario presentados en la Tabla 2 se realizan 1000 escenarios operativos que son resultados del sorteo de las variables Temperatura e Irradiancia para obtener el comportamiento del ciclo de trabajo. Para el entrenamiento del modelo de regresión lineal multi-variante, se requiere la generación de un conjunto de datos de control como se muestra en la Fig. 9. Para obtener los datos de entrada y salida se implementa el algoritmo Perturba y Observa que se encuentra embebido dentro de los bloques del ejemplo “Microgrid Hybrid PV/ Wind / Battery Management System”, de la librería de Matlab. Este conjunto de datos consta de múltiples variables independientes tal como se detalla a continuación:
Donde:
Minería de Datos
En esta etapa se presenta la metodología implementada para realizar el entrenamiento del regresor lineal multi-variante para obtener la característica adaptativa del control MPPT.
Considerando el comportamiento no lineal del ciclo de trabajo, en la presente metodología se propone realizar el entrenamiento del regresor, sobre una base de datos que son resultados de un análisis de conglomerados como se describe en la siguiente ecuación.
Donde:
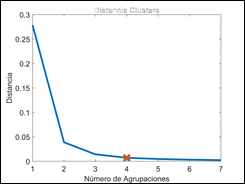
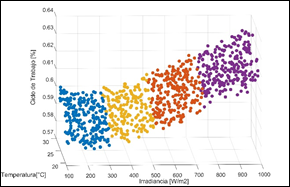
Para escoger el número de agrupaciones adecuadas para representar el universo de escenarios del comportamiento del ciclo de trabajo en función de la temperatura e irradiancia, se realiza un análisis de la distancia acumulada entre los datos de un mismo grupo con su centroide. En la Fig. 10 se presenta el comportamiento de la distancia en función del número de centroide. De este análisis se escoge cuatro centroides, considerando que la variación de distancia es muy pequeña al escoger un mayor número de grupos.
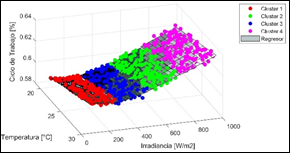
Con la ayuda de Matlab 2022b, se emplea la herramienta “kmeans” sobre la base de datos elaborada, con el requerimiento de cuatro centroides, resultados que se muestran en la Fig. 11.
Una vez que se cuenta con cuatro grupos representativos se toman de forma aleatoria el 80% de los datos de cada grupo para realizar el entrenamiento y el 20% para validación del modelo, de este entrenamiento se obtienen los resultados expuestos en la Tabla 3:
Los datos presentados en la Tabla 3 permiten representar en la Fig. 12 los planos asociados a los regresores entrenados, sobre la base de datos.
Casos de estudio
Una vez que se cuenta con los parámetros de los regresores se realiza el algoritmo propuesto de MPPT en un software de simulación de sistemas de potencia cuya respuesta puede ser observada en cantidades instantáneas, se utiliza el software de transitorios electromagnéticos HYPERSIM. Para esto se han modelado dos escenarios:
Sistema fotovoltaico conectado a red infinita
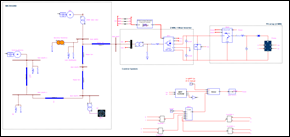
En el contexto de un modelo fotovoltaico conectado a una red infinita, se plantea una configuración en la que la instalación fotovoltaica está vinculada a una red eléctrica de dimensiones teóricamente ilimitadas. Este tipo de conexión permite que la energía generada por el sistema fotovoltaico se inyecte directamente en la red, contribuyendo así a la oferta total de energía disponible. La interconexión con una red infinita sugiere la capacidad de absorber toda la energía generada por el modelo fotovoltaico sin restricciones, en la Fig. 13 se muestra el diagrama del modelo propuesto:
Sistema fotovoltaico integrado a una Microrred
En el ámbito de un sistema fotovoltaico incorporado en una microrred, se describe una disposición en la que el panel solar forma parte de una red eléctrica de escala local. Esta microrred puede operar de forma autónoma o estar conectada a la red principal, y la contribución del modelo fotovoltaico se canaliza hacia la generación de energía dentro de este entorno más reducido. La conexión a una microrred proporciona una mayor flexibilidad y capacidad de gestión local sobre la generación, distribución y consumo de energía, permitiendo una administración más eficiente y sostenible de los recursos energéticos dentro de la comunidad o área específica a la que sirve la microrred. El modelamiento realizado incluye generación fotovoltaica con control MPPT, generación eólica, generación hidráulica y los alimentadores de distribución hacia las cargas, como se observa en el diagrama de la Fig. 14.
DISEÑO Y SIMULACIÓN
A continuación, se presenta el detalle del diseño y simulación del algoritmo propuesto de MPPT implementado en el entorno de simulación HYPERSIM el cual permite el modelamiento y análisis de redes complejas de energía proporcionando resultados para la validación y estudios de estabilidad en sistemas de pequeña y gran escala. En particular, se ha empleado la plataforma HYPERSIM para la simulación de sistemas eléctricos de potencia, aprovechando la flexibilidad y capacidad de representación detallada que ofrece. La integración con modelos específicos de MATLAB/Simulink proporciona una metodología integral para evaluar la eficiencia y robustez del algoritmo MPPT propuesto en un entorno representativo de sistemas de energía solar permitiendo evaluar su dinámica dentro de la red.
Para verificar la eficacia del algoritmo de seguimiento y su respuesta dentro de los parámetros de la red eléctrica se propone el modelamiento en dos escenarios de conexión del sistema fotovoltaico, el primero el punto de conexión común será en una barra infinita y el segundo dentro de una microrred conforme se detalla en la sección 3.
Algoritmo MPPT con conexión a red infinita
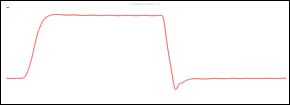
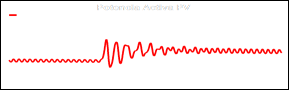
En primer lugar, el sistema propuesto se simulo con condiciones meteorológicas base de: Irradiancia (S) con un valor de 1000 W/m2 y una temperatura de 25 ⸰C, en el instante de tiempo t=0.5 segundos se realiza un cambio tipo escalón en el valor de irradiancia (∆S=100 W/m2) y temperatura (∆T=5 ⸰C) simulando una condición climatológica y vuelve a su estado inicial después de un tiempo ∆t=0.2 segundos, en este escenario se observan la respuesta del algoritmo MPPT propuesto. En las figuras: Fig. 15, Fig. 16, Fig. 17 y Fig. 18 se muestran las variables de potencia de salida, voltaje, corriente del PV y la respuesta del ciclo de trabajo calculado por el algoritmo MPPT en el clúster No 3 respectivamente:
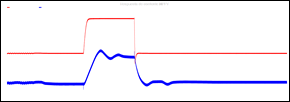
La respuesta de potencia activa en el punto común de conexión ante el escalón de irradiancia y temperatura provoca el funcionamiento del algoritmo MPPT mediante regresión lineal el mismo que modifica el ciclo de trabajo del inversor que se conecta a la red exigiendo al panel la máxima potencia, en base a esto la Fig. 16 muestra la exigencia de corriente al panel fotovoltaico durante el aumento de la temperatura y de la irradiancia.
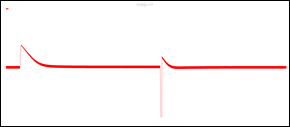
La respuesta de voltaje que se muestra en la Fig. 17 tiene una respuesta transitoria ante el cambio de corriente, dado que el inversor mantiene el voltaje de panel fotovoltaico en el estado estacionario el voltaje permanece constante.
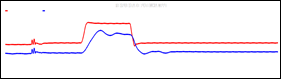
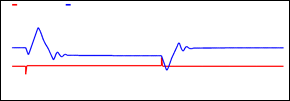
Adicionalmente se compara la respuesta transitoria causadas por los elementos de electrónica de potencia de los sistemas de control de los conversores e inversor del panel fotovoltaico, en la cual se concluye que al utilizar un algoritmo MPPT basado en Machine Learning permite eliminar los transitorios y el sobrepico de corriente que se produce en un algoritmo P&O al momento de un cambio en los parámetros de entrada en la Fig. 19 y Fig. 20 se muestra la comparación de estas señales en los dos algoritmos, para la etapa transitoria y estacionaria.
La respuesta en estado transitorio es mejorada con el algoritmo MPPT mediante regresión lineal haciendo que el inversor exija una respuesta de corriente adecuada. Adicionalmente en la Tabla 4 se presenta el aumento de potencia máxima transferida en estado estacionario en los dos métodos aplicados, concluyendo que el clúster No. 3 del regresor lineal entrenado tiene una mejor respuesta que el algoritmo perturba y observa.
Tabla 4: Comparación de respuesta de potencia activa
| Método | Potencia Activa (MW) | Porcentaje de ∆P (%) |
| Regresor Lineal | 1.038 | 29 |
| Perturba y Observa | 0.953 | 19 |
Finalmente, para este escenario se realiza una falla en el alimentador de la carga analizando para esta perturbación externa al sistema fotovoltaico como responde el algoritmo de MPPT, en la Fig. 21 se describe este cambio que muestra un adecuado comportamiento en el algoritmo propuesto en el presente trabajo.
Algoritmo MPPT con conexión a Microrred
La respuesta del sistema fotovoltaico conectado a una microrred se caracteriza por su dinámica compleja y su interacción con las condiciones variables de la microrred. En este caso la variabilidad temporal de las condiciones climáticas influirá en la generación renovable que forma parte de la microrred en este sentido el cambio en los parámetros de radiación solar y temperatura interactuaran con el resto de los elementos en la red, el análisis se centra en la capacidad del seguimiento del punto de máxima potencia ante esta nueva condición de red.
El evento realizado en este escenario corresponde al cambio tipo escalón del valor de irradiancia del panel fotovoltaico al instante de tiempo t=0.5 segundos, las respuestas dinámicas en la microrred se ven alteradas dado que el control del inversor necesita ser sintonizado para ser un formador de red ante la variación causada por las demás generaciones en este sentido en las figuras: Fig. 22, Fig. 23 y Fig. 24 se presentan las respuestas de la potencia, voltaje y corriente del panel fotovoltaico respectivamente con la implementación del algoritmo MPPT propuesto, como se puede observar el punto de potencia activa no cambia significativamente dado que la variación absorbida por la red ser reparte entre todas las fuentes de energía, esto se refleja también en el cambio de corriente exigida al inversor del panel fotovoltaico:
Se realiza además la comparación del funcionamiento de los dos métodos MPPT para observar su funcionamiento y desempeño en la configuración de Microrred, en los resultados de potencia activa trasmitida de la Fig. 25 se observa como el algoritmo P&O tiene una respuesta errónea tendiendo a una inestabilidad en el valor de potencia, en cambio, el algoritmo propuesto tiene un mejor control en la respuesta de la potencia inyectada a la microrred.
CONCLUSIONES Y RECOMENDACIONES
El algoritmo de seguimiento del punto máximo de potencia de un panel fotovoltaico exhibe una respuesta robusta y eficiente, permitiendo que la dinámica del panel fotovoltaico se adapte a las variaciones de las condiciones climatológicas y de la red, en estas condiciones el algoritmo basado en regresión lineal proporciona un mejor rendimiento para la optimización de los sistemas fotovoltaicos.
Los resultados obtenidos de las pruebas y análisis realizados en el entorno de simulación de HYPERSIM brindan evidencia sólida y respaldan la viabilidad y eficacia del algoritmo propuesto. Estos resultados muestran mejoras en la eficiencia del seguimiento del punto de máxima potencia (MPPT), la capacidad del algoritmo para adaptarse a variaciones ambientales, como cambios en la irradiación solar y temperatura. Estos resultados, derivados de la simulación en HYPERSIM, constituyen una base robusta y confiable que respalda la aplicación práctica del algoritmo propuesto en la optimización de sistemas fotovoltaicos dentro de entornos de microrred. Además, estas conclusiones sólidas proporcionan una sólida dirección para investigaciones futuras en esta área específica.
Con la finalidad de buenas prácticas, se recomienda para futuros trabajos la evaluación del comportamiento del algoritmo en un entorno controlado utilizando equipos físicos, aprovechando la ventaja de la presente aplicación en el software HYPERSIM, el cual permite simulaciones en tiempo real. Esta evaluación práctica facilitaría una comprensión más profunda del rendimiento y la eficacia del algoritmo en condiciones reales, proporcionando perspectivas de resultados valiosos que permitan validar su aplicabilidad y ajustes necesarios en la implementación en sistemas