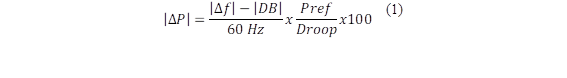INTRODUCCIÓN
En los últimos años, la Corporación Nacional de Electricidad, CELEC EP, emprendió la construcción de grandes plantas de generación hidroeléctrica en el Ecuador (incluida la central Coca Codo Sinclair de 1500 MW), las cuales entraron en operación comercial de forma paulatina desde el año 2016. Además, la incorporación del sistema de transmisión a nivel de 500 kV ocasiona cambios en las condiciones operativas del Sistema Nacional Interconectado (SNI). Sumado a esto, se proyecta la construcción de bloques de generación renovable que se caracterizan por la intermitencia en el recurso primario (irradiación solar, viento, caudal) [1].
En este escenario, ante perturbaciones, el sistema eléctrico se encuentra expuesto a condiciones de alto estrés que eventualmente podrían ocasionar la pérdida de la seguridad del sistema y, como consecuencia, interrupción parcial o total de la energía eléctrica [2]. En este sentido, resulta necesario disponer de mecanismos que permitan garantizar un grado de seguridad fiable durante la operación del sistema eléctrico. Uno de los aspectos fundamentales a ser mejorados es la respuesta dinámica del sistema ante desbalances entre generación y carga, mediante la correcta actuación de la Regulación Primaria de Frecuencia (RPF), considerando los requerimientos mínimos de la regulación nacional y normas internacionales [2].
En la Regulación No. ARCERNNR 004/20 (Codificada) denominada: “Planificación operativa, despacho y operación del sistema eléctrico de potencia” se establecen las disposiciones generales que deben cumplirse con relación a la planificación operativa, el despacho y la operación del sistema eléctrico de potencia [3]. En el artículo 13 “Criterios de calidad, seguridad, confiabilidad y economía” se detallan los criterios de calidad, donde se menciona que: “Todas las unidades de generación que se encuentren en operación deben responder de forma continua ante variaciones de la frecuencia que se presenten como resultado de eventos que causen desbalances entre la generación y la carga”.
Adicionalmente, en la sección 21 de la Regulación Nro. ARCERNNR 001/23: “Régimen de Transacciones Comerciales en el Sector Eléctrico Ecuatoriano” se plantea el “Tratamiento comercial de servicios complementarios” [4]. En esta sección se menciona que: “En el caso de que un generador no cumpla con la RPF, deberá compensar al o a los generadores que suplieron esta deficiencia…”.
Para el cumplimiento de estos requerimientos, es necesario el desarrollo de metodologías que permitan sintonizar los parámetros de los controles potencia - frecuencia para brindar una respuesta adecuada [5], estos controles son conocidos como reguladores de velocidad o gobernadores, los cuales actúan de forma local en los generadores para realizar la RPF. Con estos antecedentes, se propone una metodología para realizar la identificación y sintonización de reguladores de velocidad mediante un modelo de optimización, el cual permitirá cumplir con los requerimientos mínimos de respuesta exigidos en la normativa internacional y futuro código de red.
Existen distintas aproximaciones para la identificación de los parámetros de los modelos dinámicos, en [6] se enumeran los métodos clásicos de identificación ante pruebas de impuso, paso, de onda senoidal y respuesta en frecuencia; siendo uno de los métodos más usados, el de mediciones directas ante respuestas de impulso y paso. En las propuestas, [7], [8] se realiza la identificación a través de respuestas de impulso debido a la relativa facilidad de inyectar la señal de tipo pulso en el sistema de control.
Los algoritmos de optimización heurística son ampliamente usados para resolver este tipo de problemas, por ejemplo en [8] se utiliza el “Hybrid Cuckoo Search” para identificar el sistema turbina-gobernador y sistema de excitación de una central a gas. Por otro lado, en [9], [7], [10] se utiliza el algoritmo heurístico “Mean-Variance Mapping Optimization” (MVMO). En estas metodologías se utiliza el DIgSILENT PowerFactory para simular la respuesta dinámica, cuyos resultados se comparan con registros de eventos o pruebas controladas, obtenidos de unidades de medición fasorial (PMUs, por sus siglas en inglés). Sin embargo, estas metodologías se han orientado únicamente a la validación de modelos y no a la sintonización de sistemas de control considerando nomas y regulaciones.
Por otro lado, desde el punto de vista de sistemas de control, existen varias técnicas para sintonizar controladores PID, por ejemplo, métodos de Ziegler & Nichols, Cohen-Coon, Sintonización Lambda, Amigo, entre otros [11]. Estos métodos hacen uso de las características de repuesta del sistema en lazo abierto y en lazo cerrado, siendo las técnicas de Ziegler & Nichols las más conocidas y utilizadas [12]. Sin embargo, estas metodologías se basan en un conjunto de reglas y ecuaciones analíticas de sintonización, las cuales no llegan a una respuesta optima del sistema de control. En [13] se sugiere que los parámetros calculados con dichas técnicas pueden servir como punto de partida para la aplicación de un algoritmo genético para la sintonización óptima del controlador PID, logrando un menor número de iteraciones del algoritmo, lo que se traduce en un menor costo computacional.
Por último, existe una gran variedad de trabajos de sintonización de sistemas de control que utilizan directamente algoritmos de optimización heurísticos. Por ejemplo, [14] utiliza el MVMO para la sintonización de los estabilizadores de sistemas de potencia (PSS, por sus siglas en inglés) y para ello utiliza un modelo Generador - Barra Infinita (SMIB, por sus siglas en inglés) simplificada. Por otro lado, en [15] se propone un método de ajuste de los parámetros de control de un generador hidroeléctrico aislado considerando la respuesta primaria de frecuencia y respuesta de pequeña señal, sin considerar el cumplimiento de normativa.
En la segunda sección de este trabajo, se propone la revisión de los conceptos de estabilidad de frecuencia y el análisis de la normativa internacional respecto a la sintonización de reguladores de velocidad. En la tercera sección se realiza una revisión de los conceptos y de sintonización de reguladores. En la cuarta sección se plantea una metodología que abarca el protocolo de pruebas y un modelo de optimización para realizar la identificación y sintonización del sistema de control. En la quinta sección se presenta el análisis de resultados aplicados a la central hidroeléctrica Coca Codo Sinclair. Finalmente, se presentan las principales.
REGULACIÓN DE FRECUENCIA
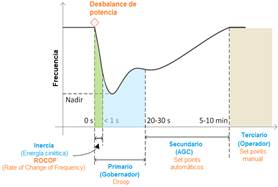
Un Sistema Eléctrico de Potencia (SEP) debe mantener el equilibrio entre la generación y la demanda a fin de garantizar un funcionamiento seguro y estable. Cuando existe un “exceso/déficit” de generación, usualmente provocado por el aumento o disminución de demanda o perdida de generación, la frecuencia del sistema se ve afectada disminuyendo o aumentando su magnitud a un valor diferente a la nominal . Por esta razón, el problema de control de frecuencia (control P-f) se relaciona con la potencia despachada por los generadores y se organizan en tres niveles: primario, secundario y terciario, tal como se muestra en la Fig. 1.
En los instantes iniciales, tras producirse un desbalance de generación-carga, la tasa de cambio de la frecuencia ROCOF (Rate of Change of Frequency) y el punto más bajo de la frecuencia alcanzado (NADIR), están determinados principalmente por la magnitud del desbalance, la inercia total del sistema, el amortiguamiento de la carga y por dispositivos de respuesta rápida como el BESS (Battery Energy Storage Systems). Paralelamente, actúan los reguladores de velocidad (también llamado gobernador o “governor” en inglés, GOV), recuperando el balance entre la generación y la carga y, ubicando la frecuencia en un nuevo punto de operación. Este control primario opera entre los 20 y 30 segundos [2], [18].
Posteriormente, actúa el control secundario en el ámbito de área de control (AGC) regulando la frecuencia y el intercambio de potencia con áreas vecinas [19]. Este control opera entre 5 y 10 minutos. Por último, actúa el control terciario en tiempos superiores a los 10 minutos, recuperando el estado normal del sistema con las con niveles de reservas óptimos [2], [18].
Regulador de Velocidad (GOV)
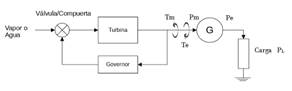
En la Fig. 2 se muestran los componentes del sistema de generación que actúan con el control de GOV. Cuando existe un desbalance instantáneo entre la potencia eléctrica (Pe) y la potencia de carga (PL) se produce un cambio en el torque eléctrico de salida (Te) del generador, produciendo una desigualdad con el torque mecánico (Tm). Esta desigualdad de torques provoca una variación de la velocidad angular del rotor y, por ende, la variación de la frecuencia [16], [20].
El GOV censa el cambio de velocidad y envía una señal de control al sistema de válvulas/compuertas con la finalidad de regular el flujo de la energía primaria que llega a la turbina. Como consecuencia, el Tm de la turbina se iguala al Te ejercido por PL, logrando así, que la velocidad retorne al valor deseado [16], [21].
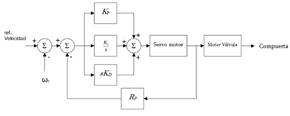
La mayoría de los reguladores electro-hidráulicos de velocidad se basan en el control PID (Proporcional-Integral-Derivativo), en lazo cerrado con el droop de velocidad (Rp), tal como se muestra en la Fig. 3 [16]. Este controlador calcula continuamente el error entre una señal medida y una de referencia, y modula la respuesta mecánica. Para ello, cada bloque del PID tiene una función específica:
Bloque Proporcional (K P ): Produce una acción de control proporcional al error medido. Su influencia en el sistema de regulación de velocidad es inmediata y significativa.
Bloque Integral (K I /s): Produce una acción de control acumulativa cuya velocidad es proporcional a la magnitud del error de entrada. En conjunto con el bloque proporcional determina la estabilidad de la respuesta del regulador de velocidad. Desde el punto de vista del error, el bloque integral recorta la entrada del error al controlador para determinar la precisión de estadio estacionario del sistema de regulación.
Bloque Derivativo (sK D ): Su acción de control es proporcional a la tasa de cambio del error. Su acción permite extender los límites del regulador de velocidad al permitir ganancias de los bloques proporcional e integral más grandes.
Droop, también conocido estatismo (Rp): Relaciona el incremento relativo (por unidad) de velocidad ∆ω o de frecuencia ∆f y el incremento relativo de potencia de salida ∆P. Por ejemplo, si Rp es 4% significa que ante una variación de frecuencia del 4% se produce un cambio de la potencia de salida del 100% [16].
Normativa Internacional
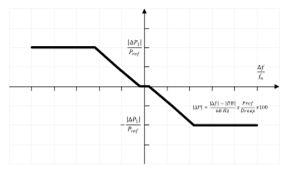
Las características de acción de los reguladores de velocidad ante un evento que requiera RPF están descritas en distintas normas internacionales y códigos de red. Para el desarrollo de la metodología propuesta se presenta, analiza y modela la regulación de la Comisión Europea [22]. En la Fig. 4 se muestra la curva característica de regulación de frecuencia, donde se muestra los principales parámetros para la verificación de la capacidad de respuesta, tales como:
Droop: ajustable en el rango de 3 a 8%.
DB: La banda muerta de la respuesta de frecuencia entre la cual el regulador de velocidad no ejercerá ninguna acción, la cual se especifica en el rango de frecuencia de 0-200 mHz.
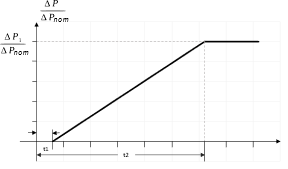
|ΔP1|/Pref: intervalo de respuesta a la frecuencia, donde ΔP1 es la respuesta en potencia activa esperada ante un desvío de frecuencia Δf (ver Fig. 5). Se considera un intervalo entre 1% y 10%. Δf: desvío de la frecuencia f respecto de 60 Hz. ΔP1: respuesta en potencia activa esperada ante un desvío de frecuencia (Δf) calculada a través de la ecuación (1).
Pref: potencia de referencia del sistema analizado, puede ser igual a la nominal de la máquina.
Pnom: potencia nominal de la máquina.
Retraso inicial (t1): tiempo de activación de la respuesta de frecuencia. Este tiempo se mide desde que se detecte un cambio de frecuencia hasta cuando se produzca una variación del 1% del ΔPensayo (ver Fig. 5). t1 debe ser menor a 2 seg.
Tiempo de activación total (t2): tiempo de activación de la respuesta de regulación a un cambio de frecuencia Δf del cual se espere una respuesta igual a |ΔP|/Pref (incluyendo el retraso inicial t1). A efectos de la determinación del t2 se considerará el tiempo correspondiente al último valor de P que entra dentro de la banda ±1% de Pref alrededor de |ΔP1|/Pref (ver Fig. 5). t2 debe ser menor a 30 seg
IDENTIFICACIÓN Y SINTONIZACIÓN DE SISTEMAS DE CONTROL
El objetivo de la identificación es modelar el sistema de control de forma tal que, la simulación sea razonablemente semejante al resultado de un evento o prueba controlada [9]. Por otro lado, el proceso de sintonización del modelo requiere de una comprensión profunda del proceso que se está modelando y el propósito para el cual se utilizará el modelo [7]; esto con la finalidad de encontrar los parámetros adecuados para un correcto funcionamiento, cumpliendo normas y códigos de red .
Debido a la compleja naturaleza de la dinámica, donde se deben resolver ecuaciones algebraico diferenciales, el problema de optimización se caracteriza por ser discontinuo, multimodal y no-convexo [23]. Por esta razón, la identificación paramétrica de los modelos dinámicos se ha basado en problemas de optimización utilizando herramientas heurísticas.
En este trabajo, para la sintonización de los sistemas de control se plantea un modelo de optimización utilizando algoritmos heurísticos cuya función objetivo puede adaptarse al cumplimiento de respuesta de escalón unitario o curva de tipo rampa unitaria, mediante la valoración de índices de rendimiento del sistema de control.
Algoritmos Heurísticos
Los métodos de optimización heurística son de propósito general muy flexibles y aplicables a la gran mayoría de problemas de optimización [24], [25]. La optimización heurística se utilizan para resolver problemas de gran tamaño, dinámico, discontinuo, multimodal y no-convexo [23].
En este trabajo se propone el uso del paquete “pymoo”, el cual cuenta con una colección de algoritmos de optimización heurística para resolver problemas de tipo mono-objetivo y multiobjetivo. Pymoo está programado en leguaje Python y contiene varios algoritmos de optimización [26], lo cual permite ahorrar tiempo de programación, facilitar el lenguaje de programación, realizar comparaciones de algoritmos y evitar los errores de implementación.
Este paquete, mediante rutinas de programación, se enlaza con PowerFactory. El PowerFactory permitirá simular la respuesta dinámica de sistema de generador-gobernador, cuya respuesta será comparada con la respuesta de la prueba en campo (identificación paramétrica) y con la rampa de RPF requerida en la norma (sintonización del control). Para que el algoritmo encuentre una óptima sintonización se puede utilizar diferentes funciones objetivas basados en índices de rendimiento.
Índices de Rendimiento
La respuesta de un sistema de control se considera óptima cuando el ajuste de sus parámetros resulta en la minimización de su índice de rendimiento, los cuales se presentan en la Tabla 1.
La minimización del error de los criterios de rendimiento ha sido ampliamente usada en la sintonización de controladores del tipo PID [10], [13], [27]-[30]. Estos criterios permiten convertir el problema de sintonización en uno de optimización, en donde: e(t) es la diferencia entre la señal obtenida (mediante simulación o medición) y una señal ideal de tipo escalón unitario o rampa unitaria, y cuyo valor debe ser minimizado [31], [32].
El criterio ISE es estricto con los grandes errores iniciales lo que lo hace ideal para identificar señales con sobreoscilaciones (también conocidos como overshoots). Por otro lado, el criterio ITSE tiene errores iniciales grandes debido a su dependencia del tiempo; en este caso, este criterio es estricto a medida que avanza el tiempo, puesto que la penalización es más severa. En cambio, el criterio IAE es el más fácil de implementar, sin embargo, su desempeño no es bueno, ni tampoco equiparable al resto de índices. Por último, el criterio ITAE tiene la particularidad de ser permisivo con los grandes errores iniciales, así como de ser severo con los errores que ocurren más adelante. Estas características del criterio ITAE permite una mejor selectividad en la búsqueda de los parámetros del sistema [33]-[35] y, es el más recomendable para utilizarlo en la sintonización de sistemas de control.
METODOLOGÍA PROPUESTA
En esta sección se presenta una descripción de la metodología propuesta para la Identificación Paramétrica y la Sintonización de los reguladores de velocidad.
Pruebas controladas y captura de datos
Durante la operación en tiempo real del sistema eléctrico, casi todas las decisiones tomadas dependen de las predicciones obtenidas de simulaciones. Estas simulaciones deben basarse en los modelos matemáticos de los sistemas con el fin de garantizar respuestas lo suficientemente precisas y, en consecuencia la toma de decisiones de control más convenientes [36], [37].
Para lograr este objetivo se realiza la identificación paramétrica de los componentes del sistema eléctrico, tarea que puede realizarse mediante registros de alta resolución y sincronizados en el tiempo para lo cual se utilizan dispositivos electrónicos inteligentes de monitoreo y de alta resolución, a partir de mediciones registradas por equipos de medición sincrofasorial (PMUs) , y enviados a un sistema de monitoreo de área extendida (WAMS), como por ejemplo, el WAMS de CENACE basado en registros de PMUs. Estos registros se caracterizan por ser sincronizados en el tiempo y tener una frecuencia de muestreo de hasta 60 Hz (16.6 ms/medida), lo cual permite inspeccionar fenómenos electromecánicos, cuyos datos permiten modelar correctamente la dinámica de los sistemas de control.
Para la intervención de la central y lectura de las señales se considera idóneo el conexionado y protocolo de pruebas definido en [9]. En este protocolo, todos los equipos se conectan directamente con el sistema WAMS de CENACE, WAProtector [38], para su almacenamiento, sincronización y análisis a través de los despliegues diseñados en la interfaz gráfica realizada para las pruebas.
Identificación Paramétrica y Sintonización
Con los resultados de las pruebas es posible realizar la identificación paramétrica y, en caso de NO cumplir con la normativa, realizar la correcta sintonización de los sistemas de control. El método de identificación paramétrica y sintonización de este trabajo se basa en la propuesta de la referencia [36], sin embargo, es importante destacar que, en este trabajo se realizan mejoras importantes como: 1) utilizar el paquete “pymoo” que permite escoger diferentes algoritmos de optimización, y; 2) utilizar diferentes funciones objetivo (índices de rendimiento) que pueden adaptarse al cumplimiento de respuesta de escalón unitario o curva de tipo rampa unitaria.
Debido a la naturaleza compleja del sistema de potencia, el problema de optimización podría NO ser abordado de manera exitosa por varios de los algoritmos de optimización heurística, así como, el problema podría NO encontrar una respuesta óptima con diferentes funciones objetivo. En este sentido, la metodología propuesta permite abordar, tanto la evaluación de diferentes funciones objetivo, así como la utilización de diferentes métodos de optimización.
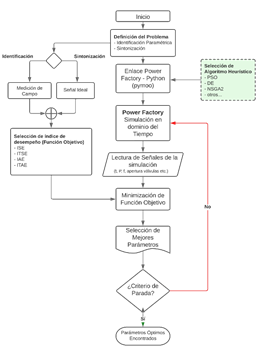
En la Fig. 6 se muestra el diagrama de flujo de la herramienta propuesta, donde se puede definir el problema resolver: 1) identificación paramétrica en base a una señal de prueba de campo o, 2) sintonización considerando una curva escalón o rampa como señal objetivo, tal como la mostrada en la Sección 2.2. (Normativa). Adicionalmente, la herramienta permite seleccionar un método de penalización para el problema de optimización (selección de función objetivo a minimizar) como, por ejemplo, los índices de desempeño ISE, ITSE, IAE o ITAE.
Para obtener la señal simulada se enlaza el software PowerFactory a través de su interfaz con Python. En Python se programa el script con los índices de desempeño y algoritmos de optimización de la librería pymoo. En el PowerFactory se realizan simulaciones en el dominio del tiempo, cuyos resultados son comparados con la referencia (prueba de campo o curva ideal). Para cada iteración del algoritmo de optimización heurístico se valoran los índices de desempeño (función objetivo) hasta alcanzar un criterio de parada, el cual puede ser un error mínimo o un número de iteraciones dado.
ANÁLISIS DE RESULTADOS
En esta sección se presenta el análisis de resultados al aplicar la metodología propuesta. Para ello, se utilizan los resultados de las pruebas de campo en la unidad 8 (U8) de la central hidroeléctrica Coca Codo Sinclair.
Pruebas de Campo
En la Tabla 2. se presentan los parámetros del regulador de velocidad de los generadores que definen la característica de regulación. Además, se muestran las ganancias del control PID (Proporcional-Integral-Derivativo) que definen los tiempos de la respuesta de regulación y que se encuentran parametrizadas por el fabricante. Con estos parámetros se realiza el análisis de resultados, cumplimiento de normativa y validación del modelo de control.
Tabla 2: Parámetros del regulador de velocidad
| Característica de Regulación | Control PID | |||||
|---|---|---|---|---|---|---|
| Banda Muerta Frec. (mHz) | Banda Muerta Potencia (kW) | Estatismo (%) | Límite |ΔP1|/Pref: (%) | kp | Tn | Td |
| 300 | 300 | 4 | 100 | 0.4 | 25 | 0 |
La banda Muerta de Potencia (DP) se encontraba parametrizada en 300 (kW); sin embargo, se parametriza en 0 (kW) debido a que no se especifica en la normativa de la sección 2.2. Por otro lado, la Banda Muerta de Frecuencia (DB) se encontraba con un valor de 300 (mHz) cuyo valor esta fuera del rango especificado en normativa (0 a 200 mHz); por esta razón, se realiza un análisis estadístico del comportamiento de la frecuencia en estado estable y estado de contingencia con la finalidad de definir la DB.
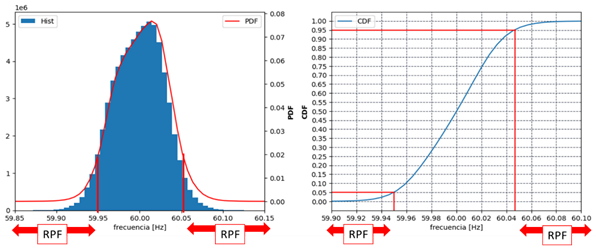
En la Fig. 7 se muestra la Función de Densidad de Probabilidad (PDF, Probability Density Function) y la Función de Probabilidad Acumulada (CDF, Cumulative Density Function) de la frecuencia, desde el 10 de marzo de 2023 hasta el 10 de abril de 2023. Se considera que la frecuencia puede oscilar de forma normal entre 59.95 Hz y 60.05 Hz, cuyos valores corresponden a la media ± dos veces la desviación estándar (Desigualdad de Chebyshev). Los valores fuera de este rango corresponden a eventos de frecuencia, donde el sistema Generador-Gobernador deben actuar aportando a la RPF; con este antecedente, se considera como DB el valor de 50 mHz. En la CDF se puede observar que, para el período analizado, la frecuencia tiene un 5% de probabilidad de salir de la DB por sub-frecuencia; de la misma manera, por sobre-frecuencia se tiene el 5% de probabilidad de que la frecuencia salga de la DB. En resumen, con una DB de 50 mHz se tiene 10% de probabilidad de actuación del Gobernador para regular la frecuencia.
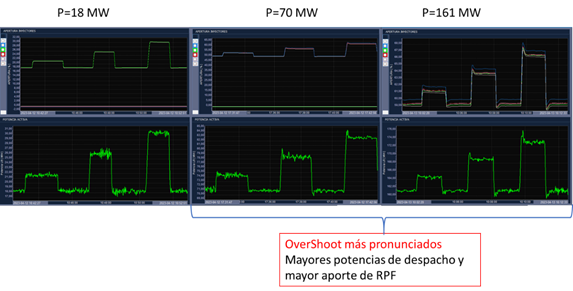
En la Fig. 8 se presenta la respuesta del generador U8, despachado con diferentes potencias (18 MW, 70 MW y 161 MW). En esta figura se observa: 1) en la gráfica superior, la apertura de válvulas (%) y 2) en la parte inferior, la respuesta de potencia activa (MW) ante decrementos de frecuencia de 0.09 Hz, 0.14 Hz y 0.19 Hz. Se aprecia una correcta actuación del regulador de velocidad, puesto que, ante el decremento de frecuencia, la unidad de generación aumenta su potencia de salida. Sin embargo, es importante notar que a mayores potencias de despacho y mayor aporte de RPF, se detecta una mayor sobre oscilación (Overshoot), que pueden excitar modos de oscilación de baja frecuencia.
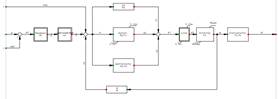
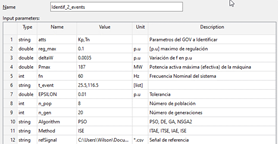
Para la identificación paramétrica se usa un sistema de control de librería que se indica en la Fig. 9, el cual está compuesto de un control PID, banda muerta y limitador de amplitud (límite de aporte a la RPF). El gobernador de la central CCS tiene 3 modos: funcionamiento sin carga, con carga y red aislada. Estos tres modos de operación requieren de distintos parámetros del PID para su operación. Tomando en cuenta esto, la identificación es realizada para el modo con carga en donde el control PID tiene deshabilitada la ganancia derivativa. Al sistema de control de la Fig. 9 se le anula el bloque derivativo del PID y se procede con la identificación paramétrica de una señal de referencia, la cual es tomada de una prueba correspondiente a una Δf=-0.19 Hz. En la Fig. 10 se muestra la máscara de la herramienta programada, donde se pueden ingresar algunos parámetros para escoger el algoritmo de optimización, el criterio de desempeño, número de iteraciones, entre otros parámetros importantes.
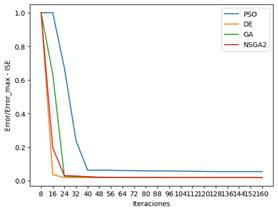
En la Fig. 11 se compara la evolución de las soluciones de los distintos algoritmos heurísticos, donde se aprecia que a medida que transcurren las iteraciones el error entre la señal de referencia y la obtenida por simulación disminuye. Además, se observa que el algoritmo de optimización DE (Differential Evolution) presenta mejor desempeño, puesto que encuentra un mínimo local en menor número de iteraciones y en menor tiempo. Por otro lado, se puede observar que el algoritmo PSO (Particular Swarm Optimization) no llega a un valor aceptable de minimización respecto a los algoritmos DE, GA (Genetic Algorithm) y NSGA2 (Non-dominated Sorting Genetic).
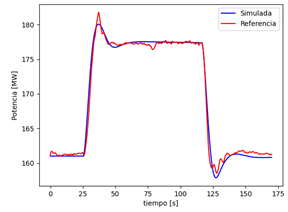
En la Fig. 12 se presenta una comparación entre la señal obtenida mediante mediciones (prueba de campo) y la señal simulada con los parámetros identificados con el algoritmo Evolución Diferencial (DE). Los parámetros del sistema de control PI identificados por los diferentes algoritmos se encuentran en la Tabla 3, donde se corrobora que el menor error (minimización de la función objetivo) se encuentra en los algoritmos DE y GA.
Tabla 3: Parámetros Identificados del GOV
| Algoritmo | Kp | Tn | Error Acum. ISE | Error ISE (p.u.) |
| PSO | 5.925 | 0.748 | 95.37 | 0.0532 |
| DE | 3.889 | 0.481 | 92.15 | 0.0176 |
| GA | 3.678 | 0.454 | 92.28 | 0.0177 |
| NSGA2 | 2.357 | 0.289 | 95.25 | 0.0183 |
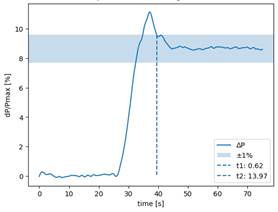
A continuación, se realiza el análisis del cumplimiento de la normativa y futuro código de red, presentado en la sección 2.2. Con este antecedente, en la Tabla 4 y Fig. 13 se presentan los análisis de los tiempos de retraso t1 y activación t2. Si bien los tiempos identificados cumplen con la normativa, en la Fig. 13 se observa que existe una sobreoscilación (overshoot) que alcanza el valor de 11.14% del valor de consigna por acción de sistema de control. Este overshoot podría provocar oscilaciones de baja frecuencia (excitación de modos de control) no deseadas en el sistema, razón por la cual se propone una sintonización de los parámetros del regulador de velocidad.
Tabla 4: Tiempos de Accionamiento del regulador de velocidad
| Parámetro | Valor | Normativa | Cumplimiento |
|---|---|---|---|
| Retraso Inicial t1 | 0.62 [s] | < 2 [s] | Si |
| Tiempo de Activación Total t2 | 13.97 [s] | < 30 [s] | Si |
Sintonización
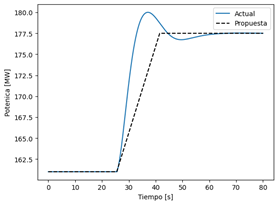
En la sintonización se configura el setpoint ideal de respuesta de la RPF (t2) en 16 segundos, valor que se encuentra dentro de los límites sugeridos la normativa y con el cual se espera reducir el overhoot inicial. En la Fig. 14 se presenta una comparación entre la respuesta actual obtenida de la identificación paramétrica y la curva ideal propuesta, esto permitirá retrasar la respuesta del sistema de control y evitar el overshoot.
En la Fig. 15 se presentan las respuestas de sintonización del algoritmo de optimización PSO conforme se incrementan el número de iteraciones. Se observa que, a medida que transcurren las iteraciones el indicador de rendimiento el ITAE disminuye el error, puesto que la respuesta simulada se acerva a la respuesta ideal propuesta (señal de referencia). Los parámetros encontrados en esta sintonización se presentan en la Tabla 5.
En la Fig. 16 se comparan las señales obtenidas en: medición de campo (prueba en color azul), identificación paramétrica (color rojo) y sintonización propuesta (color negro). Se observa que, la nueva propuesta alcanza el valor de consigna de forma más lenta, sin embargo, es más importante destacar que ya no presenta overshoot.
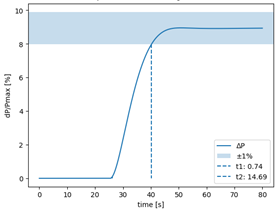
Por último, es importante destacar que, la nueva propuesta de sintonización cumple con los tiempos de retraso y activación de la RPF, cuyas respuestas y análisis se pueden observar en la Fig. 17.
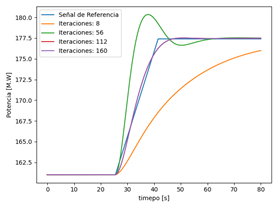
Figura 15: Respuestas del regulador de velocidad alcanzadas en algunas iteraciones del algoritmo heurístico
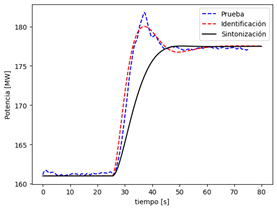
Figura 16: Comparación entre señales obtenidas: en mediciones de campo (azul), identificación paramétrica (rojo) y nuevos parámetros obtenidos de la sintonización (negro)
ANALISIS DE ROCOF Y NADIR
La propuesta de sintonización implica que la respuesta dinámica del sistema sea diferente lo que afecta la frecuencia mínima alcanzada (NADIR) al hacerla más baja y la pendiente de caída de la frecuencia (ROCOF) al hacerla más pronunciada. Para evaluar la afectación al sistema se llevaron a cabo simulaciones de contingencias n-1 con la salida de las centrales Agoyan con un despacho de 146 MW y San Francisco con 212 MW en un equivalente dinámico del SIN.
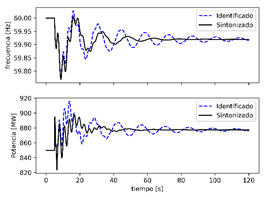
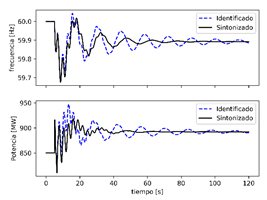
En la Fig. 18 y Fig. 19 se presentan la respuesta frecuencia del sistema y la respuesta primaria de frecuencia de la central Coca Codo Sinclair ante la salida de las centrales. En la Tabla 6 se presenta una comparativa entre los valores del ROCOF y NADIR entre los nuevos parámetros propuestos para sintonización y los identificados.
CONCLUSIONES
Se verifica que el protocolo de pruebas propuesto en [9] es robusto y permite la verificación y actuación dinámica del regulador de velocidad, puesto que, se obtienen medidas en tiempo real de las señales de: potencia eléctrica, frecuencia y apertura de válvulas de agua, permitiendo realizar la correcta identificación paramétrica y sintonización del regulador de velocidad mediante programación en Python y enlazando la simulación dinámica con PowerFactory de DIgSILENT. A partir del protocolo de pruebas establecido y la obtención de las respuestas reales del sistema Generador-Regulador de Velocidad, se pueden identificar todas las restricciones que limitan la correcta actuación de la RPF.
Adicionalmente, es importante destacar que se desarrolla una herramienta que permite realizar, tanto la identificación paramétrica con datos de pruebas reales, así como, la sintonización de los GOVs utilizando respuestas ideales que cumplen con los requerimientos de la normativa. Comitentemente, esta herramienta permite escoger diferentes algoritmos de optimización y diferentes funciones objetivo (índices de rendimiento). Esto permite buscar la mejor respuesta del regulador cambiando funciones objetivo y utilizando diferentes algoritmos de optimización, logrando de esta manera, ampliar los espacios de búsqueda y comparar dichas respuestas.
En el análisis del ROCOF y el NADIR se puede observar que a pesar de que el ROCOF es idéntico entre los eventos con los parámetros propuesto e identificados, el NADIR es ligeramente mas bajo con los parámetros propuestos pero en una magnitud muy pequeña, así mismo se puede observar en la Fig. 18 y Fig. 19 que la respuesta de la frecuencia es más amortiguada por lo que se puede concluir que una pequeña disminución en el NADIR permite mejorar la respuesta dinámica de la frecuencia en el sistema.
Por último, es importante mencionar que la guía de IEEE [39] propone evaluar el rendimiento del sistema de control mediante la respuesta en frecuencia, lo cual implica someter el sistema de control a señales senoidales de diversas frecuencias. Si bien el modelo identificado logra representar con precisión el comportamiento del sistema físico en el dominio del tiempo, no se presenta la respuesta en el dominio de la frecuencia. Para realizar un análisis en el dominio de la frecuencia se debe modelar el diagrama de bloques control a detalle y, en este caso se utiliza un modelo simplificado. No obstante, se plantea como una perspectiva para futuros trabajos, el desarrollo de un protocolo y una metodología específica para llevar a cabo esta evaluación.