INTRODUCCIÓN
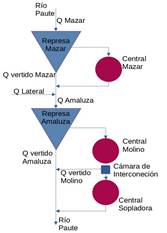
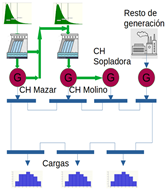
El complejo hidroeléctrico más importante del Ecuador es el Complejo Paute Integral, conformado por 3 centrales en cascada sobre el río Paute. Este complejo proporciona el 35% de la energía eléctrica al Sistema Nacional Interconectado del país [1] gracias a la producción de las centrales: Mazar de 170 MW, Molino de 1 100 MW y Sopladora de 487 MW (véase Fig. 1). Se aprovecha el caudal del río Paute entre la cota 2 153 m.s.n.m. y la cota 925 m.s.n.m. Durante este trayecto se han construido dos represas para almacenar y regular el recurso hídrico [2].
Como se demuestra más adelante, el río Paute es un típico río de montaña, que se caracteriza por ser estacional y con gran variabilidad de los caudales diarios e incluso horarios. Bajo estas condiciones, la precisa operación de los niveles de los embalses es fundamental, intentando aprovecha al máximo la energía renovable y barata del agua y así obtener un precio de generación de energía óptimo del Sistema Eléctrico de Potencia (SEP), sin arriesgar el normal abastecimiento de la demanda del país.
En países con alta dependencia de la energía hidráulica, como Brasil, Canadá, Australia, Ecuador, entre otros, se han desarrollado diversos estudios y propuesta que optimizan el despacho hidrotérmico tanto en el corto, mediano y largo plazo. El despacho hidrotérmico, en cualquiera de sus modalidades, pretende minimizar el costo total de generación (presente y futuro) en su específico horizonte de tiempo. Estos estudios generalmente se aplican a las condiciones reales de una instalaciones [3], demostrando la bondad de sus propuestas con datos verdaderos.
Fuente: [4]
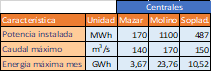
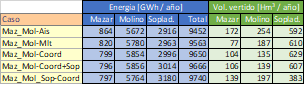
Las principales características de las represas del complejo Paute Integral se presentan en la Tabla 1 y de las centrales en la Tabla 2. Se aclara que por seguridad del sistema eléctrico ecuatoriano se restringe el nivel mínimo de operación de las represas a valores más conservadores y de esta manera se crea una energía de contingencia que serviría para emergencia.
Dada las características de las centrales y los embalses del Complejo Paute Integral, la mayor optimización energética se conseguirá con un adecuado despacho en el mediano plazo, ya que su embalse principal, llamado Mazar, tiene la capacidad de abastecer de agua a las centrales durante varios meses. No así el embalse Amaluza, que, por su tamaño, tiene una regulación semanal. Por fortuna está ubicado aguas abajo del embalse Mazar y, por tanto, gran parte del agua que recibe está previamente regulado.
Una optimización del despacho hidrotérmico a mediano plazo (MTHD, por sus siglas en inglés) no se conoce que se haya documentado para Ecuador, y consecuentemente, este artículo presenta la comparación de dos metodologías diferentes para este mismo fin. La primera es una propuesta probabilística, cuyo objetivo es obtener reglas operativas que reduzcan el valor de riego (VaR) del costo de la generación anual del sistema eléctrico nacional [5]. La segunda es una optimización del despacho mediante la determinación de niveles objetivo para cada día del año. Para ambos casos se introducen aspectos prácticos tomados de la experiencia de la operación real de las centrales. Finalmente se realiza una comparación de los dos métodos.
El presente trabajo se desarrolla como sigue: en la Sección 2 se presenta los conceptos y el estado del arte del despacho hidrotérmico, resaltando lo relacionado al MTDH y las dos metodologías utilizadas en este trabajo. Un estudio hidrológico del río Paute es presentado en la Sección 3. La aplicación y resultados del MTHD probabilístico se presenta en la Sección 4. La Sección 5 presenta el MTHD propuesto en base a niveles óptimos diarios. Finalmente, las principales conclusiones y recomendaciones se señalan en la Sección 6.
DESPACHO HIDROTÉRMICO
El despacho hidrotérmico de un SEP ha sido estudiado ampliamente. En la década de 1980 se propuso métodos de programación dinámica [6], se trató también con variables estocásticas [7], también para el despacho a corto plazo [8], y para el despacho de centrales en múltiples represas [9]. Posteriormente se mejoraron las técnicas para afrontar de mejor manera la magnitud del problema [10]. En esencia se busca determinar la energía que producirán las centrales térmicas y las hidráulicas a fin de obtener el menor costo operativo del sistema, en un cierto período de tiempo. Recientemente, se han incorporado restricciones ambientales [11]; nuevas técnicas de optimización a fin de obtener mejores y más eficientes algoritmos [12]; consideraciones de la operación de tiempo real [13]; optimizaciones estocásticas [14]; o mediante algoritmos evolutivos [15].
El problema del despacho hidrotérmico se lo puede plantear a corto, mediano o largo plazo, cada uno con sus particularidades y beneficios. En el corto plazo, la atención principal se centra en superar las horas pico (peak shaving) con el menor incremento de energía térmica, ya que su costo unitario se incrementa al aumentar la cantidad requerida. Se determina una planificación horaria que respete los límites operativos de todo el sistema y que permita llegar a cumplir objetivos, generalmente semanales, para las plantas hidráulicas dependientes de sus embalses y afluencias.
En el MTHD generalmente el estudio se lo realiza a pocos meses o años (generalmente un año), y su objetivo es determinar reglas operativas estacionales [16], analizar la influencia de la salida de operación de alguna instalación importante durante varias semanas o meses [17] o establecer índices de seguridad operativos. La información que se dispone es más certera que la utilizada para un estudio a largo plazo y se basa en la proyección semanal o mensual de la demanda, del recurso hídrico, disponibilidad de la infraestructura, y demás variables necesarias para esta planificación.
El despacho hidrotérmico a largo plazo, el horizonte suele ser de 5 o más años y su objetivo es analizar alternativas de expansión del sistema eléctrico, así como el efecto de incorporar nueva infraestructura al SEP. Las proyecciones se basan en datos históricos, escenarios de crecimiento económico y/o proyectos grandes que influencien en el suministro o demanda de energía. Las variables suelen tener resolución trimestral o anual.
Este trabajo se centra en el MTHD ya que su objetivo es presentar optimizaciones de despacho para el Complejo Hidroeléctrico Paute Integral, en donde la regulación de su embalse principal (embalse Mazar) es de varios meses. En este sentido, un aprovechamiento óptimo del recurso hídrico disponible se logrará mediante una precisa gestión de los embalses para reducir los vertimientos y mejorar la producción.
Enfoque probabilístico para el MTHD
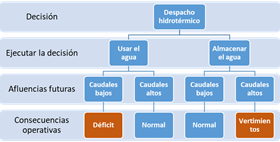
Dado que la afluencia de los ríos que se aprovechan para la generación hidráulica, así como la demanda de energía futura a ser abastecida son variables estocásticas, parece natural tratar el MTHD con un enfoque probabilístico. La disyuntiva para cualquier despacho hidrotérmico es: qué es mejor, utilizar el agua de los embalses ahora, o usarla en el futuro. La Fig.2 presenta las implicaciones operativas de esta decisión.
Fuente: [5]
El enfoque probabilístico exige que se determinen las variables estocásticas con la mejor información disponible para que sean representativas tanto para el comportamiento presente como para el futuro de estas variables. Para esto se cuenta con datos históricos de los caudales diarios desde el año 1964, lo que es usado para determinar la distribución de probabilidad de los caudales afluentes para cada mes del año de cada embalse en estudio.
La demanda del sistema no es difícil de predecir para el mediano plazo. Es necesario revisar el comportamiento mensual de los últimos años y establecer su tendencia y estacionalidad, finalmente se proyecta para 1 o 2 año futuros, que es el horizonte de tiempo planteado en un MTHD.
Ahora se debe conocer la variable objetivo para el MTHD probabilístico, y para este estudio será el valor medio del costo de generación anual del SEP. Para esto, se debe encontrar el despacho económico para cada una de las simulaciones de Monte Carlo, donde se asigna aleatoriamente valores a las variables (afluencias a los embalses y demanda de energía). El resolver el despacho económico implica encontrar el costo mínimo de producción, sujeto a las restricciones de satisfacer la demanda, respetar límites operativos de: embalses, centrales, líneas de transmisión, entre otros. Las variables de estado que permiten esta optimización son los volúmenes turbinados en cada mes por cada central. Estas variables determinan si el agua es utilizada en este mes o es almacenada para el futuro. Resuelto el despacho económico, los valores obtenidos son almacenados para conformar distribuciones de ingresos de generación, de donde se puede determinar el valor medio así como el valor de riesgo (VaR), y distribuciones de generación anual de cada central.
Para afrontar de manera eficiente este problema, se realizan algunas aproximaciones, como son: desacoplar la potencia activa de la reactiva en el SEP, y no se consideran las limitaciones del sistema de transmisión. Además, se modela a todos los demás generadores de energía como uno solo con un costo adecuado de generación. Los detalles se presentan en la Sección 4.
Nivel de embalse diario óptimo
Un segundo método es propuesto por el autor para optimizar el MTHD del Complejo Hidroeléctrico Paute Integral. Las políticas de operación de embalses se han estudiado desde varias perspectivas. La programación dinámica [6] y la programación dinámica estocástica [7] fueron propuestos años atrás, también se trataron metodologías tradicionales de control como la de bucle cerrado [17], pasando por programación lineal, y programación dinámica que incluye los efectos del mercado [18], también a un modelo estocástico se incluyó caudales auto regresivos [14], incluso técnicas de inteligencia artificial se han empleado [19]. Las funciones objetivos también pueden ser diversas, dependiendo de los usos que el agua tenga como destino, incluso pueden ser aplicadas a un reservorio multipropósito [20]. Igualmente se puede tratar de un arreglo de reservorios conectados entre ellos. La mayor complejidad de los algoritmos se justifica por la mayor complejidad de las funciones objetivo a resolver y de los datos de entrada, el tamaño del SEP, y se los aplica a reservorios reales ya que siempre existen características especiales en cada estudio [21].
Para el caso del Complejo Paute Integral el uso del agua es puramente energético, lo que permite buscar reglas operativas centradas en la optimización de la producción de las 3 centrales sobre el río Paute, respetando sus restricciones operativas.
Se propone como variables de estado a los niveles que los embalses en estudio deben alcanzar para el primer día de cada mes del año. Por interpolación lineal, entre estos niveles para dos meses consecutivos, se determina el nivel objetivo para cada día del año.
El modelo simula el comportamiento diario del complejo para todo el histórico de caudales y en base a los caudales afluentes, la diferencia entre el nivel real de los embalses y sus niveles objetivos diarios se determina el despacho de cada central. Como función objetivo a optimizar se ha definido la producción energética media anual, de la central o centrales bajo análisis. Se obtiene también el volumen medio anual de agua vertida en cada embalse al aplicar los niveles óptimos.
Otras opciones de funciones objetivo pueden ser exploradas, por ejemplo, los ingresos monetarios del complejo hidroeléctrico. Además, con este trabajo se desea presentar la transformación que sufren las reglas operativas de los embalses según varíen las condiciones de operación entre las diferentes centrales del complejo o se incorpore nueva infraestructura. Los detalles se presentan en la Sección 5.
HIDROLÓGIA DEL RÍO PAUTE
La cuenca del río Paute es las más estudiada en el Ecuador debido a la gran importancia energética que posee. Estos estudios han sido validados y actualizados en varias ocasiones debido a que cada nuevo proyecto de infraestructura requiere su justificarse técnica y económica y su punto de partida es la hidrología. Es así que se cuenta con datos de caudales desde el año 1964 hasta la fecha; sin embargo, se ha cortado la información hasta el año 2020. A continuación, se caracteriza los caudales registrados durante estos 57 años de historia en los puntos de interés del río Paute.
La represa Mazar, ubicada en el río Paute antes de la unión del río Mazar (Paute A.J. Mazar), está emplazada a 2 010 m.s.n.m. en el río Paute y se construyó entre los años 2006 y 2010. Sus objetivos principales son: regular el recurso hídrico hacia la Central Molino, y controlar los sedimentos que arrastra el río. Este embalse ha marcado un gran cambio en el despacho hidrotérmico del país, ya que a más de incorporar una central de 170 MW, permite una planificación a mediano plazo por la regulación trimestral del embalse.
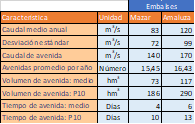
Las características principales de la serie de caudales diarios registrados se presentan en la Tabla 3. La variabilidad alta de los caudales, a nivel diario e incluso horario es una característica típica de los ríos de montaña.
A pesar de la alta variabilidad de los caudales diarios, al analizar el comportamiento de los caudales mensuales, se observa un comportamiento estacional. Al graficar los caudales medios mensuales y su desviación estándar (como porcentaje del caudal medio mensual) se obtiene la Fig.3. Se destaca que el período húmedo se define en los meses de abril a agosto y los meses más secos son diciembre y enero.
Para finalizar el estudio hidrológico de la cuenca de río Paute A.J. Mazar, se caracterizan las avenidas o crecidas que se producen en este punto. En primer lugar se define en este trabajo como avenida cuando el caudal de ingreso a la represa es superior a la capacidad de turbinamiento de la central hidroeléctrica asociada. En otras palabras, cuando no es posible controlar el nivel del embalse a pesar de maximizar la producción de la central. Para el caso de Mazar, una avenida es cuando el caudal diario supera los 140 m3/s. Igualmente se establece en este estudio que finaliza una avenida cuando durante 2 días consecutivos el caudal ha caído por debajo de este valor. De esta manera se unen avenidas consecutivas o con menos de 48 horas de intervalo. Las características de las avenidas del río Paute en Mazar se pueden visualizar en la Tabla 3.
El río Paute en D.J. Palmira es precisamente en la represa Daniel Palacios o más conocida como represa Amaluza que fue construida entre los años 1972 y 1978. Las características hidrológicas de los caudales afluentes a este embalse se presentan en la Tabla 3.
Existen pocas diferencias cualitativas entre el río Paute en la represa Mazar y el río Paute en la represa Amaluza. Como es lógico, en Amaluza, al captar una cuenca de mayor área, el caudal aumenta, y también disminuye su variabilidad, como se puede ver en la Fig.4. El comportamiento estacional es el mismo, tanto en los meses más húmedos como en los más secos.
Las avenidas del río Paute en Amaluza ahora serán los caudales medios diarios superiores a 170 m3/s y los valores característicos se presentan en la misma Tabla 3.
Una vez que se ha caracterizado la hidrología del río Paute es posible explicar de mejor manera los resultados que se presentan a continuación tanto para el MTHD probabilístico como para el MTHD mediante cotas objetivo diarias óptimas en los embalses.
APLICANDO EL MTHD PROBABILÍSTICO
El Valor en Riesgo o VaR (de sus siglas en inglés) se lo define como la probabilidad, normalmente baja (entre el 1% y el 5%), de sufrir una determinada pérdida durante un período de tiempo. Sin embargo, como ya se estableció en la Sección 2, el VaR para el MTHD tiene como objetivo minimizar el costo medio de generación anual del SEP y establecer el costo de generación sujeto a una probabilidad de ocurrencia muy alta (95% de las veces o mayor).
Los pasos a seguir son los siguientes [5]:
Se genera aleatoriamente valores de caudales de afluencia para los 12 meses del año en cada represa.
Se genera los valores de demanda para cada barra de carga, también para cada mes del año.
Se realiza el despacho hidrotérmico óptimo tomando en cuenta las restricciones operativas del modelo.
Se almacena el costo de operación, la generación térmica e hidráulica.
Se itera sobre los pasos 1 a 4 hasta obtener una distribución estable.
Se presentan los resultados y su análisis.
Para resolver este algoritmo se debe disponer de los siguientes parámetros:
Costos de la energía de las centrales de generación; en este trabajo se consideran únicamente los costos variables de generación.
Restricciones operativas de los niveles de los embalses, condiciones de vertimiento, producción de las centrales, líneas de transmisión (aquí no se considera el sistema de transmisión).
Establecer la producción de las centrales en función de los niveles de los embalses y el agua turbinada (la productividad del agua para cada central).
Para resolver el MTHD, sin perder generalidad de la metodología, se aplica al Complejo Hidroeléctrico Paute Integral, se consideran las dependencias hidráulicas entre las tres centrales Mazar, Molino y Sopladora que se esquematizan en la Fig.5, se ha tomado la demanda nacional mensual del año 2019 [22] a la cual se le ha asignado una variabilidad de ±5%, y se ha representado al resto de generadores hidráulicos y térmicos como un solo generador.
A fin de representar el comportamiento natural de despacho económico se modela el precio de la energía del resto de generadores proporcional a la cantidad requerida. Para ello se consideran datos históricos de los costos variables de producción de los años 2017, 2018 y 2019 del mercado eléctrico ecuatoriano [23]. El costo de la energía se establece como 0,015 veces la energía requerida más 2 (en USD$/MWh), pero se debe aclara que esta relación es muy aproximada, por lo que los resultados de costos totales de generación son ficticios. Para las centrales del complejo Paute Integral el costo de producción es fijo en USD$ 2 por MWh.
Adicionalmente, se presenta los límites operativos de los embalses y se ha calculado el volumen turbinable mensual máximo para cada central. Para esto se ha incorporado un factor de seguridad del 10%, es decir, debido a indisponibilidades de los generadores (2%), baja carga en la madrugada y reserva de potencia para AGC (regulación secundaria de frecuencia, 4%) no es posible turbinar más del 90% de la capacidad instalada. Estos valores se los puede observar en la Tabla 4.
Finalmente, se ha obtenido la productividad del agua en cada una de las centrales, a partir de datos de diseño y construcción de cada instalación. La productividad considera las pérdidas hidráulicas, mecánicas y eléctricas de cada central y es obtenida para diferentes condiciones operativas. Con esta gran variedad de muestras se ha ajustado una ecuación cuadrática para estimar la productividad del agua en cada central.
Mediante una selección de los caudales diarios para cada mes del año, de los 57 años de historia utilizados en este trabajo, se ajusta la mejor curva de distribución para cada mes y para cada caudal afluente. Para este estudio, se determina los caudales afluentes del río Paute A.J. Mazar para el embalse Mazar, y el caudal lateral del embalse Amaluza. Al realizar el ajusta para determinar las distribuciones de probabilidad de las 24 variables de caudales, todas las distribuciones quedaron definidas como Lognormal, la cual se caracteriza por 3 parámetros: ubicación, media y desviación estándar. Estos parámetros se presentan en la Tabla 5.
Con estos parámetros y siguiendo los algoritmos descritos al inicio de esta Sección, se presenta (en la Fig.6) la función de distribución del costo de generación anual del SEP, para el MTHD óptimo. Se destaca que el valor medio anual es de USD$ 400,14 MM y con una probabilidad del 95% se puede asegurar que será inferior a USD$ 459,39 MM. Esto se consigue mediante una utilización óptima de los caudales que ingresan a las represas Mazar y Amaluza.
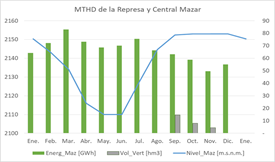
Los valores más significativos del MTHD de la represa Mazar se grafican en la Fig.7. Los niveles reportados por la metodología (o reglas de operación) son los que minimizarían los vertimientos en las represas y se puede resumir como sigue: partiendo de un nivel alto a inicio de año, consumir todo el embalse hasta el mes de abril, los meses húmedos mantener la producción al máximo, en el mes de agosto subir el nivel del embalse, en septiembre mantener el nivel alto hasta fin de noviembre y en diciembre empezar a consumir el embalse lentamente. Con esta política se obtiene una producción media anual de 676 GWh con una desviación estándar de 113 GWh.

Figura 6: Distribución de probabilidades del costo total de generación del SEP para un MTHD probabilístico
Para el embalse Amaluza, y el despacho de las centrales Molino y Sopladora, se presenta la Fig.8, en donde se observa el perfil de operación del embalse. Se puede resumir como regla de operación, que se debe mantener el nivel del embalse cercano a la cota 1 980 m.s.n.m. (límite inferior definido en este estudio), lo cual es congruente con el estudio hidrológico en cuanto a la magnitud de las crecidas esperadas y el volumen operable de la represa. El incremento de nivel del embalse que se observa en los meses de abundancia hídrica no es voluntario, sino responde a que el volumen ingresado en esos meses es superior al límite máximo de volumen turbinable por la central, y en consecuencia se represar el agua y sube el nivel del embalse.
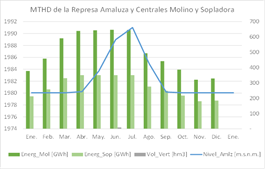
Figura 8: Principales resultados de MTHD probabilístico para la represa Amaluza y centrales Molino y Sopladora
La producción de la central Sopladora es siempre proporcional a la producción de la central Molino, con un factor de pérdida del 10% del caudal turbinado por Molino debido a la cámara de interconexión. Con esta regla operativa, se espera una producción media anual de 5 246 GWh en Molino y 2 911 GWh en Sopladora.
La generación requerida para satisfacer la demanda se la representa como un solo generador, que en realidad son todas las otras centrales de generación. Es por eso que se modela su costo con un valor inicial de $2 por MWh y un incremento proporcional a la cantidad de energía requerida, llegando a valores de hasta $26 por MWh. Con esta caracterización aproximada, que pudiera modificarse, se obtiene el precio medio de generación anual y su VaR.
Esta metodología es muy aplicable para obtener reglas operativas de mediano plazo; es decir, a partir de distribuciones de probabilidades de las principales variables de ingreso al modelo, se obtienen los niveles más probables a fin de optimizar el costo medio anual de generación. Las reglas operativas obtenidas son claras y congruentes con el análisis hidrológico.
El punto débil de esta metodología es que, debido a la modelación mensual, se aproximan todas las variables a esta escala temporal, por lo que se pierde exactitud en los resultados. Considerando esta limitación, se ha visto la oportunidad de mejorar la precisión de los valores obtenidos cambiando la simulación a una escala temporal diaria y obtener así resultados más exactos. Esta metodología se presenta en la siguiente sección.
MTHD MEDIANTE NIVELES OBJETIVOS DIARIOS PARA CADA EMBALSE
El MTHD tiene como objetivo determinar las reglas operativas de los embalses en estudio, con las particularidades propias de estas instalaciones y los caudales de la cuenca bajo análisis. Sin embargo, el método propuesto en esta sección se aplicará específicamente al Complejo Paute Integral, sin que pierda generalidad el algoritmo ya que este ejemplo presenta alta complejidad por las características que fueron descritos en las Secciones 1 y 3.
Para resolver el problema del MTHD se ha configurado como función objetivo maximizar la generación hidroeléctrica. Otras funciones objetivo también pueden ser seleccionadas, como por ejemplo maximizar los ingresos de la operación de las centrales. La metodología es idéntica, sin embargo, los resultados finales podrían diferir.
Para resolver el problema de optimización, se utiliza el software Oracle Crystal Ball, en donde se establece como variables de estado los niveles objetivos para el primer día de cada mes del año en cada embalse, y como se explicó en la Subsección 2.2 se interpolan los niveles objetivos para cada día del año. La variable objetivo es la energía media anual producida por la central o centrales bajo análisis. El algoritmo de optimización debe encontrar los niveles objetivos óptimos para maximizar la función objetivo establecida.
Ya que se desea obtener un MTHD más detallado que el de la sección anterior, se ha modelado el comportamiento de los embalses, la producción de las centrales, etc., a nivel diario y con las restricciones operativas de cada instalación: niveles máximos y mínimos de los embalses, potencias y caudales máximos y mínimos de las centrales, la potencia de generación en función de la altura neta de la columna de agua, pérdidas hidráulicas, mecánicas y eléctricas, etc. En este estudio no se ha modelado el sistema de transmisión y se establece una demanda que consume toda la energía producida. Las restricciones de producción máxima son las mismas de la sección anterior.
Con el modelo de cada central validado, y con los caudales afluentes diarios de 57 años de historia, se simula, a escala temporal diaria, el comportamiento del complejo y se calcula la producción de cada central. Se introducen las variables de decisión y la función objetivo ya explicadas y se ejecuta el proceso de optimización, que entrega como resultados los niveles objetivos óptimos para cada día de cada embalse, y la energía media anual producida por las centrales. Además, se obtiene, de manera informativa, el volumen medio anual vertido en cada embalse y en la cámara de interconexión Molino - Sopladora.
Para determinar la producción diaria, se establece el volumen disponible para cada día mediante la diferencia entre el volumen inicial y el volumen objetivo y se añade el volumen afluente del río para ese día. Ese será el volumen a turbinar, siempre y cuando no supere al volumen turbinable máximo, en cuyo caso se utiliza el valor máximo. El volumen a turbinar también puede ser modificado por la coordinación de producción entre centrales, como se presenta más adelante.
Con el objeto de establecer el impacto que tiene la incorporación de nuevas instalaciones en el MTHD y las reglas operativas de los embalses, y cómo se incorporan conceptos de coordinación entre centrales al modelo para obtener mejoras en el despacho, se presentan los resultados por etapas o pasos. Estos pasos son los siguientes: (i) Mazar y Molino aisladas; (ii) Mazar y Molino simultáneas; (iii) Mazar y Molino coordinadas; (iv) Mazar y Molino coordinadas más Sopladora; y (v) Mazar, Molino y Sopladora coordinadas. Los resultados para cada etapa se presentan en la Tabla 6.
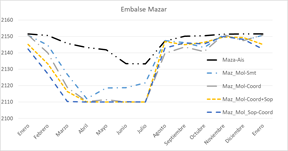
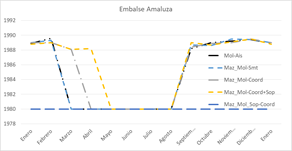
Para el primer caso (i) la optimización del MTHD se ha dividido en dos etapas: primero se optimiza la producción de la central Mazar, y a continuación se buscan los niveles para el embalse Amaluza que optimicen la producción de Molino (la producción de Sopladora no es considerada). Los resultados obtenidos se presentan en las Fig.9 y Fig.10 para los embalses Mazar (curva denominada “Maz-Ais”) y Amaluza (serie denominada “Mol-Ais”).
El siguiente caso (ii) es cambiar la función objetivo para que maximice la producción de las dos centrales simultáneamente, es decir, el algoritmo de optimización buscará encontrar una combinación de las 24 variables de estado (primer día de cada mes, en cada embalse) para obtener la mayor generación media anual de las centrales Mazar y Molino.
Como resultado de esta optimización, en la represa Mazar se reducen sus niveles objetivos (véase Fig.9 curva “Maz_Mol-Smt”). El mejor aprovechamiento del agua almacenada en Mazar determina una mejora sustancial en Molino ya que el agua en esta central tiene una productividad 4 veces superior a la de Mazar debido a la mayor altura neta del agua. Los niveles objetivos de la represa Amaluza no se ven afectados y se presenta en la Fig.10 bajo el nombre “Maz_Mol-Smt”.
En el caso (iii) la coordinación directa entre la central Mazar y la central Molino materializa uno de los objetivos básicos de la represa Mazar que es almacenar el recurso hídrico para mejorar la producción de la central Molino. Esto se consigue al condicionar el despacho de energía de Mazar para que controle el nivel de la represa Amaluza. En detalle, se deben tomar en cuenta dos condicionales: si el nivel del embalse en Amaluza esta descontrolado (2 metros por encima de su nivel objetivo) el despacho en Mazar será restringido; sin embargo, cuando el nivel en la represa Mazar está próximo al vertimiento, sobre la cota 2 152,5 m.s.n.m. (se vierte en la cota 2 153), se elimina la restricción del despacho en la central Mazar, ya que se considera que el vertimiento en la represa Mazar ya no se podrá evitar y es mejor turbinar el agua que verterla directamente.
Esta coordinación del despacho entra las centrales Mazar y Molino produce que el MTHD cuide el recurso hídrico, lo cual se visualiza como unas cotas objetivos diarias inferiores para la central Mazar (Fig.9, curva llamada “Maz_Mol-Coord”). El cuidado del agua en la represa Mazar permite que la repesa Amaluza trabaje con niveles más elevados en los meses de cambio de estación seca a húmeda y viceversa. Se observa en la Fig.10 que ahora en febrero se consume algo de agua y los meses de cambio total en el nivel del embalse Amaluza son marzo y agosto.
El propósito del siguiente caso (iv) es observar los cambios en el MTHD debido a la entrada en operación de una nueva instalación, en este ejemplo la central Sopladora. Este caso no difiere del anterior en cuanto a las políticas de despacho, únicamente se modifica la función objetivo a optimizar. Hasta el caso anterior sólo se consideraban las producciones de las centrales Mazar y Molino, ahora se incorpora la producción de la central Sopladora.
En la Fig.9 del embalse Mazar se observa en la curva llamada “Maz_Mol-Coord+Sop” una reducción de las cotas objetivos en especial en los primeros meses del año. La represa Amaluza cambia el mes de consumo del embalse al mes de abril en su MTHD con respecto al caso anterior; es decir, si la represa Mazar asegura controlar los caudales en el primer cuatrimestre del año, Amaluza podría trabajar con niveles altos.
Finalmente (caso (v)) se incorpora la coordinación entre las centrales Molino - Sopladora. La coordinación se materializa mediante la subordinación de la producción de la central Molino al caudal turbinable máximo de la central Sopladora. Como se establece en la Sección 1, el caudal turbinable máximo de la central Sopladora es de 150 m3/s; y el de la central Molino es de 170 m3/s. Por lo tanto, se subordina la producción diaria de la central Molino a no superar los 150 m3/s, salvo que el nivel del embalse Amaluza este fuera de control (a menos de 2 metros del vertimiento, es decir, a cotas superiores a la 1989 m.s.n.m.). Esta regla operativa da más valor al agua para que sea mejor aprovechada evitando desperdicios en la cámara de interconexión que alimenta a la central Sopladora.
La afección de esta coordinación en el MTHD de la central Mazar se observa en la misma Fig.9, la curva llamada “Maz_Mol_Sop-Coord” y se aprecia que los niveles óptimos se reducen ligeramente a inicios de año. El gran cambio se visualiza en el MTHD de la represa Amaluza. El cuidado del recurso hídrico obliga a que durante todo el año el nivel objetivo óptimo sea el mínimo establecido como regla operativa (como se ve en la Fig.10). A pesar de esto y como se observa en la Tabla 6, se incrementa el volumen vertido en las represas, no así en la cámara de interconexión que cae un 37%. Como resultado final de esta coordinación resulta una producción neta de 9 740 GWh en el complejo Paute Integral.
La conclusión del MTHD en base a niveles objetivos diarios óptimos de los embalses, con la operación de las tres centrales coordinadas entre ellas, presenta las siguientes reglas operativas:
El embalse Mazar:
A partir de niveles altos a inicios de noviembre, deberá consumir su embalse lentamente hasta fines de diciembre y completamente hasta marzo.
A partir de marzo intentar operar en niveles mínimos, es decir, cualquier avenida que se presente, intentar consumirla lo antes posible, pero respetando la coordinación entre centrales.
En el mes de julio subir el nivel a valores medios - altos (cota 2 140 m.s.n.m.), y durante los siguientes meses incrementar el nivel gradualmente, hasta fines de octubre, en donde se inicia el ciclo nuevamente.
Para el embalse Amaluza: debido a su reducido tamaño y su objetivo de cuidar al agua para una óptima producción en Molino y Sopladora, su regla operativa es simple, tratar de mantener el nivel del embalse en su mínimo operativo (para este estudio, la cota 1 980 m.s.n.m.), y en lo posible turbinar hasta 150 m3/s.
Como comentario adicional, se debe destacar el impacto que tiene la operación de una central sobre las que vienen en cascada; y también el sacrificio que realiza la central de cabeza a fin de mejorar la productividad de las demás centrales y lograr un despacho óptimo del complejo en su conjunto.
CONCLUSIONES
Este artículo ilustra la importancia del MTHD en la operación de un SEP, y especialmente cuando se trata de centrales en cascada con grandes asimetrías entre sus embalses y sus capacidades de producción, así como afluencias hídricas estacionales y con gran variabilidad. El caso del Complejo Paute Integral es un ejemplo muy didáctico para apreciar estas particularidades; además permite observar cómo se modifican las reglas operativas acorde a los diferentes escenarios que se configuran sobre esta infraestructura.
A pesar de que el MTHD probabilístico es una evaluación con valores mensuales tanto de las variables estocásticas como de los otros parámetros del modelo, los resultados a los que llega, en términos de reglas operativas, son coincidentes en gran medida con el modelo de MTHD mediante niveles diarios óptimos en los embalses, con una carga computacional mucho menor. Es sencillo complementar este modelo con más centrales importantes, tanto hidráulicas como térmicas, o con mayor detalle en las restricciones operativas como limitaciones en los flujos o mayor detalle en los costos de generación, a fin de desarrollar un estudio a escala nacional representativo, esto permitiría tener un MTHD para las principales centrales del sistema, el cual se lo debería actualizar al menos mensualmente.
Con la finalidad de incrementar la precisión del MTHD se mejora la representación de las centrales de generación y mediante el historial de caudales diarios, se detalla, a escala diaria, el comportamiento operativo de las centrales del Complejo Paute Integral. Con estas mejoras se desarrolla un modelo óptimo de MTHD con niveles objetivos diarios, y se lo construye por etapas a fin de analizar la congruencia de sus resultados, así como la variación de las reglas operativas producto de incluir más infraestructura en el complejo. Los resultados del modelo son congruentes tanto en reglas cualitativas como en valores de producción energética y volúmenes vertidos en los embalses.
Algo muy destacable es la coincidencia de los dos modelos de MTHD en las reglas operativas finales para los dos embalses. Para el caso del embalse Mazar: consumir el embalse entre los meses de diciembre a marzo, las crecidas de invierno evacuarlas rápidamente (a pesar de esto, es difícil evitar los vertimientos en estos meses), recuperar el embalse en el mes de julio, y completarlo hasta el mes de octubre, noviembre operar con niveles altos. Para el caso del embalse Amaluza es muy simple, intentar mantener el nivel del embalse en su valor mínimo todo el año, cada avenida que se recibe, consumirla rápidamente. Todo esto respetando las reglas de coordinación entre centrales para aprovechar al máximo el importante y limitado recurso hídrico.
Para la aplicación real de reglas operativas de un MTHD se requiere ampliar el estudio a nivel nacional o del SEP, incluyendo las principales centrales y restricciones operativas. Sin embargo, al ser el Complejo Hidroeléctrico Paute Integral el productor del 35% de la energía nacional, su optimización local tendrá un gran impacto en la operación del resto del SEP y seguramente se confirmará una reducción importante en el costo de generación del Ecuador, en especial los meses de inicio de año, cuando se consume el embalse Mazar de manera continua.